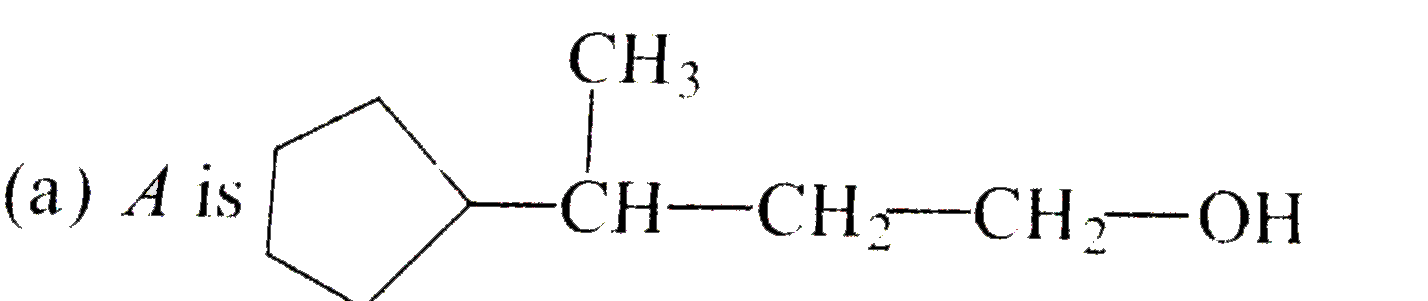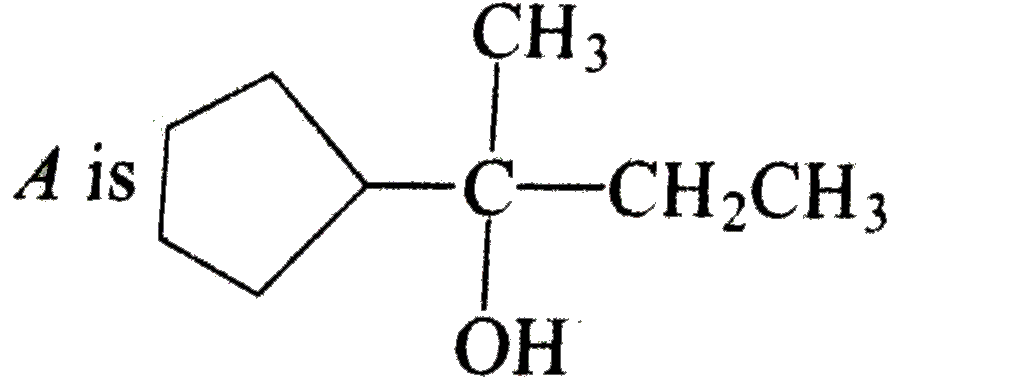Explore topic-wise InterviewSolutions in .

This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.

91601.

A 5.00 gm sample of a natural gas, consisting of methane CH_(4), and ethylene,C_(2)H_(4) was burnt in excess oxygen , yeilding 44/3 gm of CO_(2) and H_(2)O as products . What mole percent of the sample was ethylene ?

Answer»


ANSWER :`"MOLE%of ETHYLENE"=(100)/(3)%"]"`
Discussion
91602.

A 50 ml solution of pH=1 is mixed with a 50 ml solution of pH=2. The pH of the mixture will be nearly

Answer»

0.86
1.26
1.76
2.26

Answer :B
Discussion
91603.

A 50 ml solution of 0.1M acetic acid is titrated against a 0.1 M sodium hydroxide.The best indicator will be :

Answer»

Phenophthalein
Methyl orange
A SELF indicator
Methyl red

Answer :A
Discussion
91604.

A 50-ml aliquot of 0.01 M solution of HCOOH was titrated with 0.1 M NaOH. Predict the pH of the solution (a) at the beginning of the reaction, (b) at the half-equivalence point, (c) at the equivalence point, and (d) after 10 mL of the base has been added.

Answer»

SOLUTION :2.88, 3.75, 7.86, 11.92
Discussion
91605.

A 50 litre vessel is equally divided into three parts with the help of two stationary semi permeable membrane ( SPM). The vessel contains 60g H_(2) gas in the left chambe, 160g O_(2) in the middle & 140 g N_(2) in the right one . The left SPM allows transfer of only H_(2) gas while the right one allows the transfer of both H_(2) & N_(2). Calculate the final ratio of pressure in the three chambers.

Answer»


ANSWER :`4:7 : 5`
Discussion
91606.

A 50 gm oleum sample labelled as 104.5% will have mass of SO_(3)

Answer»

`80 gm`
`40 gm`
`20 gm`
`10 gm`

Solution :`104.5%` LABELLED OLEUM sample
MOLES of `H_(2)O= (4.5)/(18) = (1)/(4)` moles
`{:(,SO_(3),+,H_(2)O,rarr,H_(2)SO_(4)),("Moles",(1)/(4),,(1)/(4),,):}`
Mass of `SO_(3) = (1)/(4) xx 80 = 20 gm`
100 gm oleum has 20 gm `SO_(3)`
In 50 gm Oleum, `SO_(3)` will be 10 gm
Discussion
91607.

A 5.0 g sample of a natural gas consisting of methane (CH_(4)) and ethylene (C_(2)H_(4)) was burnt in excess oxygen, yielding 14.5 g of CO_(2) and some H_(2)O as products. Calculate the percentage of ethylene in the sample.

Answer»

Solution :Suppose ethylene `(C_(2)H_(4))` in the MIXTURE = x g
The methane `(CH_(4))` in the mixture = (5 - x) g
Equations for complete combustion of `CH_(4)` and `C_(2)H_(4)` are :
`C_(2)H(4)+3 O_(2) rarr 2CO_(2)+2H_(2)O`
`CH_(4)+2O_(2)rarr CO_(2)+2H_(2)O`
`28 g C_(2)H_(4)` PRODUCE `CO_(2)=2xx44 g = 88 g`
`therefore x g C_(2)H_(4)` will produce `CO_(2)=(88)/(28)xx x g = (22 x)/(7)g`
`16 g CH_(4)` product `CO_(2)=44 g`
`(5-x)g CH_(4)` will produce `CO_(2)=(44)/(16)xx(5-x)=(11(5-x))/(4)`
`therefore (22x)/(7)+(11(5-x))/(4)=14.5`or `88x +77(5-x)=28xx14.5`
or `11 x = 406 - 385=21` or `x=(21)/(11)`
`therefore %` of `C_(2)H_(4)=(21//11)/(5)xx100=(21)/(55)xx100=38.18 %` .
Discussion
91608.

A 5% solutionb of sucrose (C_(12)H_(22)O_(11)) is isotone with o.877% solution of urea. Calculate the molecular mass of urea (Atomic mass C=12, H=1, O=16).

Answer»


Solution :SCINCE the TWO slutions are istonic,
`pi=pi'`
`(n_(B)xxRxxT)/V=(N'_(B)xxRxxt)/(V'),n_(B)/V=(n'_(B))/(V'),W_(B)/(M_(B)xxV)=(W'_(B))/(M'_(B)xxV')`
here"" `W_(B)=5g, V=0.100 L, M_(B)("Mol. MASS of sugar", C_(12)H_(22)O_(11))=342" g mol"^(-1)`
`W'_(B)=0.877g, V'=0.100L, M'_(B)=?`
`(5g)/((342" g mol"^(-1))XX(0.1L))=((0.877g))/(M'_(B)xx(0.1L))`
`M'_(B)=((0.877g)xx(342" g mol"^(-1))xx(0.1L))/((5g)xx(0.1L))=59.99" g mol"^(-1).`
Discussion
91609.

A 5% solution of glucose ( molar mass =180 ) is isotonic with a 2.5% solution of a substance X at the same temperature. The molar mass of X is :

Answer»

90
45
180
360

SOLUTION :The two solution will have same OSMOTIC PRESSURE so that
`(5)/(180)RT=(2.5)/(M) RT` or `M=(2.5)/(5)xx180=90`
Discussion
91610.

A 5% solution of sugarcane ( mol. wt. 342 ) is isotonic with 1% solution of X under similar conditions. The molecular mass of X is :

Answer»

171.2
68.4
34.2
136.2

Solution :`pi_(1)=pi_(2)`
or `C_(1)=C_(2)`
`(5)/(342)=1/M`
`:.M=(342)/(5)=68.4`
Discussion
91611.

A 5% solution of cane sugar (molar mass 342) is isotonic with 1% of a solution of an unknown solute. The molar mass of unknown solute in g/mol is

Answer»

136.2
171.2
68.4
34.2

Solution :ISOTONIC solutions have equal molar concentrations. HENCE,
`(5//342)/(100)xx1000=(1//M)/(100)xx1000"or"(5)/(342)=(1)/(M)"or"M=68.4`
Discussion
91612.

A 5% solution of cane sugar (molar mass 342) is isotonic with 1% of a solution of an unknown solute. The molar mass oftmknown solute in g/mol is :

Answer»

`171.2`
`68.4`
`34.2`
`136.2`

SOLUTION :For isotonic SOLUTIONS
`PI _(1) =pi_(2)`
`C_(1) =C_(2)`
`(5//342)/(0.1) =(1//M)/(0.1)`
`(5)/(342) =1/M`
`impliesM =(342)/(5) IMPLIES 68.4` gm/mol
Discussion
91613.

A 5% solution of cane sugar (molar mass = 342) is isotonic with 1% solution os a substance X. The molar mass of X is:

Answer»

171.2
68.4
34.2
136.2

Solution :`pi=(W_(B)xxRxxT)/(M_(B)XXV)`
R, T and V are constants for ISOTONIC SOLUTIONS
`pi_(x)=pi_(sugar)1/M_(x)=5/342`
`or M_(X)=342/5=68.4`
Discussion
91614.

A 5% solution of cane-sugar (m. wt. = 342) is isotonic with 0.877% solution of urea. Find the molecular weight of urea.

Answer»


ANSWER :60 U
Discussion
91615.

A 5% solution of cane sugar (M. wt = 342) is isotonic with 1% solution of substance X. The molecular weight of X is:

Answer»

171.2
68.4
34.2
136.2

Answer :B
Discussion
91616.

A 5% solution of cane suger is isotonic with 0.5% of X. The molecular weight of substance X is

Answer»

34.2
119.96
95.58
126.98

Answer :A
Discussion
91617.

A 5% solution (by mass) of cane sugar in water has freezing point of 271 K. Calculate the freezing point of a 5% glucose in water if freezing point of pure wateris 273.15 K.

Answer»

SOLUTION :`5%` solution by mass means 5 G of solute is present in 100 g of solution
`therefore `Mass of solvent (Water) = 95 g
`"Molality of sugar solution "=(5)/(342)xx(1000)/(95)=0.154""("mol. Mass of sugar "C_(12)H_(22)O_(11)=342)`
`DeltaT_(f)" for sugar solution "=273.15-271=2.15^(@), DeltaT_(f)=K_(f)xxm therefore K_(f)=(2.15)/(0.154)`
`"Molality of glucose solution "=(5)/(180)xx(1000)/(95)=0.292""("mol. mass of glucose "C_(6)H_(12)O_(6)=180)`
`therefore""DeltaT_(f)" (Glucose)" =K_(f)xxm=(2.15)/(0.154)xx0.292=4.08`
`therefore"FREEZING point of glucose solution "=273.15-4.08="269.07 K."`
Discussion
91618.

A 5% solution (by mass) of cane sugar in water has freezing point of 271 K. Calculate the frezing point of 271 K. Calculate the freezing point of 5% glucose in water if freezing point of pure water is 273.15 K.

Answer»

Solution :Here, `Delta T_(f)=(273.15-271)K`
= 2.15 K
Molar mass of sugar `(C_(12)H_(22)O_(11))`
`=12xx12+22xx1+11xx16`
`= 342 g MOL^(-1)`
5% solution (by mass) of cane sugar in water MEANS 5 g of cane sugar is present in (100 g - 5)g = 95 g of water.
Now, number of cane sugar
`= (5)/(342)=0.0146` mol
Therefore, molality of the solution,
`m=(0.0146 mol)/(0.095 kg)=0.1537 mol kg^(-1)`
Applying the RELATION,
`Delta T_(f)=K_(f)m`
`therefore K_(f)=(Delta T_(f))/(m)`
`= (2.15 K)/(0.1537" K kg mol"^(-1))`
= 13.99 K kg/mol
Molar of glucose `(C_(6)H_(12)O_(6))`
`= 6xx12+12xx1+6xx16`
`= 180 g mol^(-1)`
5% glucose in water means 5 g glucose is present in (100 - 5) g = 95 g of water. Therefore, Number of moles of glucose
`= (5)/(180)` mol
= 0.0278 mol
Therefore, molality of the solution,
`m =(0.0278 mol)/(0.095 kg)`
Applying the relation,
`Delta T_(f)=K_(f)XX m`
= 13.99 K kg `mol^(-1)xx 0.2926 mol kg^(-1)`
= 4.09 K (approximately)
Hence, the freezing point of 5% glucose solution is (273.15 - 4.09) K = 269.06 K.
Discussion
91619.

A 5% solution (by mass) of cane sugar in water has freezing point of 271 K. Calculate the freezing point of a 5% glucose (by mass) in water. The freezing point of pure water is 273.15 K.

Answer»

271 K
273.15
269.07 K
277.23 K.

Solution :For both the solution `W_(B)andW_(A)` are the same.
`(DeltaT_(f(g)))/(DeltaT_(f(s)))=(M_(("suorse")))/(M_(("GLUCOSE")))`
`DeltaT_(f(g))=((342g MOL^(-1)))/((182g mol^(-1)))xx215K=4.04 K`
`"f.p. of glucose solution"=(273.15-4.-4)`
=269.11 K.
Discussion
91620.

A 5% solution (by mass) of cane sugar in water has freezing point of 271 K. Calculate the freezing point of a 5% glucose in water if freezing point of pure water is 273.15 K.

Answer»

Solution : Molality of SUGAR solution =` 5/342 xx 1000/100 = 0.146 `
`Delta T_f` for sugar solution = 273.15 - 271 = `2.15^@`
USING the following relation and substituting values, we have
Molality of glucose solution = `5/180 xx 1000/100 = 0.278`
Using the relation`Delta T_f xx K_f xx m`and substituting values again, we have
`Delta T_f ` (Glucose) ` = (2.15)/(0.146)xx 0.278 = 4.09^@`
`THEREFORE `Freezing point of glucose solution = 273.15 - 4.09 = 269.06 K.
Discussion
91621.

A 5 percent aqueous solution by mass of a non-volatile solute boils at 100.15^@C. Calculate the molar mass of the solute. K_b = 0.52 K kg mol^(-1).

Answer»

Solution :The normal boiling POINT of water is `100^@C`.
`:.`The elevation in boiling point is `0.15^@C`.
A 5 percent solution means that in a 100 g solution 5 g of the solute is PRESENT. This IMPLIES that the solvent is 95 g.
If the molar mass of the solute is M, then the molality of the solute in the solution is,
`(5//M)/95xx1000,DeltaT_b=K_bm`
`0.15=0.52xx(5//m)/95xx1000`
`:.`M = 182.4 g/mol
Discussion
91622.

A 5% by mass of an aqueous solution of A of molar mass 342"gmol"^(-1)is isotonic with 0.878% by mass of an aqueous solution of another substance B. The molar mass of B in "gmol"^(-1)is

Answer»

120
180
60
90

Answer :C
Discussion
91623.

A 4:1 molar mixture of He and CH4 is contained in a vessel at 20 bar pressure.Due to a hole in the vessel the gas-mixture leaks out. What is the composition of the mixture effusing out initially?

Answer»


ANSWER :`8:1`
Discussion
91624.

Name the metal M, which is extracted based on the following equation 4M +8CN^(-) + 2H_(2) O + O_(2) to 4 [M (CN)_(2)]^(-) + 4OH^(-)2[M (CN)_(2) ]^(-) + Zn to [Zn(CN)_(4)]^(2) + 2M

Answer»


ANSWER :AG and AU
Discussion
91625.

A 4.1 molar mixutre of He and CH_(4) is contained in a vessel at 20 bar pressure. Due to a hole in the vessel, the gas mixture leeks out. What is the composition of the mixutre effusing out initially ?

Answer»

Solution :Molar ratio of He and `CH_(4)` is 4:1
`THEREFORE` Partial PRESSURE ratio of He and `CH_(4)` is 16:4 (`because` total pressure =20 bar)
`(n_(He))/(n_(CH_(4)))=sqrt((M_(CH_(4)))/(M_(He)))xx(P_(He))/(P_(CH_(4)))` (`because` TIME of diffusion for both is same)
`=sqrt((16)/(4) xx(16)/(4))=8:1`
The COMPOSITION of mixutre initially gone out for He and `CH_(4)` is 8:1
Discussion
91626.

A 400 mg iron capsule contains 100 mg of ferrousfumarate, (CHCOO)_2 Fe. The percentage of iron present in it is approximately

Answer»

`33%`
`25%`
`14%`
`8%`

Solution :Molecular wt. of `(CHCOO)_2Fe`=170
FE present in 100 mg of `(CHCOO)_2Fe=56/170xx100` mg
=32.9 mg
This is present in 400 mg of the CAPSULE .
`therefore` % of Fe in the capsule = `32.9/400xx100`=8.2
Discussion
91627.

A 4.0 M aqueous solution of NaCl is prepared and 500 mL of this solution is electrolysed. This leads to the evolution of chlorine gas at one of the electrodes. (Na = 23, Hg = 200, 1 F = 96500 C) The following examples illustrate a typical case, involving chemical/electrochemical reaction, which requires a clear understanding of the mole concept. The total charge (coulombs) required for complete electrolysis is

Answer»

24125
48250
96500
193000

Answer :D
Discussion
91628.

A 4.0 M aqueous solution of NaCl is prepared and 500 mL of this solution is electrolysed. This leads to the evolution of chlorine gas at one of the electrodes. (Na = 23, Hg = 200, 1 F = 96500 C) The following examples illustrate a typical case, involving chemical/electrochemical reaction, which requires a clear understanding of the mole concept. If the cathode is a Hg electrode, the maximum weight (g) of amalgam formed from this solution is

Answer»

200
225
400
446

Solution :MAXIMUM MOLES of Na deposited is 2 moles and the AMALGAM is (Na-Hg).
Discussion
91629.

A 4.0 M aqueous solution of NaCl is prepared and 500 mL of this solution is electrolysed. This leads to the evolution of chlorine gas at one of the electrodes. (Na = 23, Hg = 200, 1 F = 96500 C) The following examples illustrate a typical case, involving chemical/electrochemical reaction, which requires a clear understanding of the mole concept. The total number of moles of chlorine gas evolved is

Answer»

0.5
`1.0`
`2.0`
`3.0`

ANSWER :B
Discussion
91630.

A 4% solution (w/w) of sucrose (M 342 g mol^(-1)) in water has a freezing point of 271.15K Calculate the freezing point of 5% glucose (M= 180 g mol^(-1)) in water. (Given: Freezing point of pure water 273.15 K)

Answer»

Solution :`DeltaT_(F)=K_(f)m`
`K_(f)=DeltaT_(f) xx (M_(2)xx w_(1))/(w_(2)xx1000)`
`=(2xx342xx96)/(4 xx 1000)=16.4 K`
`DeltaT_(f)=K_(f)m`
`=(K_(f)w_(2)xx1000)/(M_(2)xxw_(1))=(16.4xx5xx1000)/(95xx180)=4.8K`
`Delta T_(f)=T_(f)^(@)-T_(f)`
`4.8=273.15-T_(f)`
`T_(f)=268.35K`
Discussion
91631.

A 4% solution of sucrose is isotonic with 3% solution of an unknown organic substance. Calculate the molecular mass of unknown substance.

Answer»

Solution : As the solutions are isotonic, the molarities of the two solutions are equal.
`M_("sucrose") = M_("UNKNOWN")`
`4/342 XX 1000/100 = 3/x xx 1000/100`
` x = (3 xx 342)/(4) = (3 xx 171)/(2) = 513/2 = 256.5 g "MOL"^(-1)`
Discussion
91632.

A 4% solution of non-volatile solute is isotonic with 0.702% urea solution Calculate the molar mass of the non-volatile solute. (Mola.r mass of urea = 60 g mol^(-1))

Answer»

SOLUTION :`M_(2)=341.8g" "MOL^(-1)`
Discussion
91633.

A 4 % solution of sucrose C_(12)H_(22)O_(11) is isotonic with 3 per cent solution of an unknown organic substance. Calculate the molar mass of the unknown substance.

Answer»

Solution :Since the two solutions are isotonic, they must have same concentrations in moles/litre.
For sucrose solution, we gave`""` Concentration `=4g//100cm^(3)"(GIVEN) = 40 g/litre "=(40)/(342)" moles/litre"`
`""(because" Molar mass of sucrose, "C_(12)H_(22)O_(11)="342 g mol"^(-1))`
For unknown substance, suppose M is the mol. mass. Then
Concentration = `3g//100cm^(3)"(Given)= 30 g/litre"=(30)/(M) "moles/litre"`
THUS, we have `(30)/(M)=(40)/(342) or M=(30xx342)/(40)="256.5 g mol"^(-1)`
Discussion
91634.

(a) 3d Transition metals and their compounds are good catalysts. Give two reasons?2(b) Give the formula for the calculation of spin only magnetic moment.

Answer»

Solution : (a) (1) Because of large SURFACE area(2) VARIABLE valency
(b)`mu =SQRT( N(n+2))` n=no of unpaired electrons.
Discussion
91635.

(A) 369 K is considered as transition temperature of sulphur (R ) At 369 K both alpha and betasulphur are exist in equilibrium

Answer»

Both (A) and (R ) are true and (R ) is the CORRECT explanation of (A)
Both (A) and (R ) are true and (R ) is not the correct explanation of (A)
(A) is true but (R ) is false
Both (A) and (R )are false

ANSWER :A
Discussion
91636.

A 3.42% (wt./vol.) solution of cane suger is isotonic with a 5.96% (wt./vol.) solution of raffinose. The molecular weight of raffinose is:

Answer»

59.6
596
5.96
5960

Answer :B
Discussion
91637.

A 34.0 L cylinder contains 212 g O_(2) gas at 27^(@)C. What mass of O_(2) (g) must be released to reduce the pressure to 2.463 atm?

Answer»

103.2 g
108.8 g
100.0 g
32.0 g

Answer :B
Discussion
91638.

A 3.2 cm^(3) solution of H_(2)O_(2) liberates 0.58 gm of iodine from acidified Kl solution calculated the strength of H_(2)O_(2) solution in termsof volume strength at STP

Answer»


Solution :`H_(2)O_(2) + KI` shows the following change
`2I^(-) to I_(2) + 2E`
`O_(2)^(-) + 2e to 2O^(2-)`
or `H_(2)O_(2) + H_(2)SO_(4) + 2Kl to K_(2)SO_(4) + I_(2) + 2H_(2)O`
Now meq. Of `H_(2)O_(2)`=meq. Of `I_(2)`
`Nxx3.2=(0.508 g)/(254//2)xx1000 :. N_(H_(2)O_(2)) =4/3.2 =1.25 eq//L`
`:. W_(H_(2)O_(2))=(1.25xx34)/2=21.25 g//L =0.02125 g//mL`
`:. 68 g H_(2)O_(2)` GIVES `O_(2)` at NTP =22400 mL
`:. ` 0.02125 g or 1mL `H_(2)O_(2)`
gives `O_(2) =(22400xx0.02125)/68 =7mL`
`:. ` volume strength of `H_(2)O_(2) =7mL`
Discussion
91639.

Answer any three of the following questions. a) 31 g of an unknown molecular material is dissolved in 500 g of water. The resulting solution freezes at 271.14 K. Calculate the molar mass of the material. Given : K_t for water =1.86"KK gmol1" T_(t)^(@) of water =273K.

Answer»

SOLUTION :`M_2 = (k_f xx w_2 xx 1000)/(Delta T_f xx w_1)`
`M_2 = (1.86 K kg mol^(-1) xx 31.0 g xx 1000 g kg^(-1))/(1.86 K xx 500 g)`
`M_2 = 62 g mol^(-1)`
(b) When a pressure more than the osmotic pressure is applied on a concentrated solution solvent flows from the concentrated solution to dilute solution through semi PERMEABLE membrane/ pure solvent flows out of the solution through semi permeable membrane if a pressure LARGER than the osmotic pressure is applied.
Desalination of WATER.
Discussion
91640.

(a) 31 g of an unknown molecular material is dissolved in 500 g of water. The resulting solution freezes at 27.14 K. Calculate the molar mass of the material. [Given: K, for water 1.86 Kgmol^(-1), T_(f)^(0) of water=273К].(b) What is reverse osmosis? Mention its use.

Answer»

Solution :(a)`M_(B) = K_(f)W_(B)1000/DeltaT_(f)W_(A)`
`Delta(T)_(f) =``T^(0)_(f) - T_(f)=273-271.14K=1.86K`
`M_(B)= 1.86xx31xx1000/(1.86xx500)=62gmol^(-1)`
Discussion
91641.

A 3.00 g sample containing Fe_(3)O_(4), Fe_(2)O_(3)and an inert impure substance, is treated with excess of KI solution in presence of dilute H_(2)SO_(4) . The entire iron is converted into Fe^(2+) along with the liberation of iodine. The resulting solution is diluted to 100 mL. A 20 mL of the dilute solution requires 11.0 mL of 0.5 M Na_(2)S_(2)O_(3) solution to reduce the iodine, present. A 50 mL of the dilute solution after complete extraction of the iodine required 12.80 mL of 0.25 M KMnO_(4) solution in dilute H_(2)SO_(4) medium for the oxidation of Fe^(2+) . Calculate the % of Fe_(2)O_(3) "and" Fe_(3)O_(4) in the original sample.

Answer»

Solution :The FOLLOWING reactions are involved in given DATA
`Fe_(2)O_(3) + 3H_(2)SO_(4) rarr Fe_(2)(SO_(4))_(3) + 3H_(2)O, FeO + H_(2)SO_(4) rarr FeSO_(4) + H_(2)O`
`Fe_(2)(SO_(4))_(3) + 2KI rarr 2FeSO_(4) + K_(2)SO_(4) + I_(2)`
`I_(2) + 2Na_(2)S_(2)O_(3) rarr 2 NaI + Na_(2)S_(4)O_(6)`
`2KMnO_(4) + 8H_(2)SO_(4) + 10FeSO_(4) rarr K_(2)SO_(4) + 2MnSO_(4) + 5Fe_(2)(SO_(4))_(3) + 8H_(2)O`
1 mole `Fe_(2)O_(3)` = 1 mole `Fe_(2)(SO_(4))_(3)` = 1 mole of `I_(2)` = 2 moles of `Na_(2)S_(2)O_(3)` and 5 moles of `FeSO_(4)` = 1 mole of `KMnO_(4)`
Number of millimoles of `I_(2)` in 20 mL = `5.5 xx 1/2 = 2.75 `
So, the number of millimoles of `I_(2)` in 100 mL = `2.75 xx 100/20 = 13.75`
Number of millimoles of `Fe_(2)O_(3) = 13.75`
Number of moles of `Fe_(2)O_(3) = 13.75 xx 10^(-3)`
Suppose x moles of `Fe_(3)O_(4)` and y moles of `Fe_(2)O_(3)` are present in 3g sample. In this sample `Fe_(3)O_(4)` is an equimolar mixture of FeO and `Fe_(2)O_(3)`. Therefore, total number of moles of `Fe_(2)O_(3)` in the mixture = x + y
`x + y = 13.75 xx 10^(-3)`........ (i)
Number of millimoles of `KMnO_(4) = 0.25 xx 12.80 = 3.2`
Number of millimoles of `FeSO_(4)` in 50 mL = `3.2 xx 5 = 16` and number of millimoles of `FeSO_(4)` in 100 mL = `16 xx 100/50 = 32`
1 mole `Fe_(2)SO_(4)` gives 3 moles of `FeSO_(4)` and 1 mole of `Fe_(2)O_(3)` gives 2 moles of `FeSO_(4)`
`3x + 2y = 32 xx 10^(-3)`........ (ii)
On solving EQUATIONS (i) and (ii)
Number of moles of `Fe_(3)O_(4)` in the mixture `(x) = 4.5 xx 10^(-3)`
Number of moles of `Fe_(2)O_(3)`in the mixture `(y) = 9.25 xx 10^(-3)`
Mass of `Fe_(3)O_(4) = 4.5 xx 10^(-3) xx 232 = 1.044 g`
and Mass of `Fe_(2)O_(3) = 9.25 xx 10^(-3) xx 160 = 1.480 g`
` % of Fe_(3)O_(4) = 1.044/3.00 xx 100 = 34.8 %`
and `% of Fe_(2)O_(3) = 1.480/3.0 xx 100 = 49.33 %`
Discussion
91642.

A 300 K the vapour pressure of an ideal solution containing 1 mole of liquid A and 2 moles of liquid B is 500 mm of Hg. The vapour pressure of the solution increases by 25 mm of Hg if one more mole of B is added to the above ideal solution at 300 K. Then vapour pressure of A in its pure state is :

Answer»

300 mm of Hg
40 mm of Hg
500mm of Hg
600 mm of Hg.

Solution :ACCORDING to Raoult.s law,
`p=p_(A)^(@) x_(A)+p_(B)^(@) x_(B)`
`p=500` mm Hg, `x_(A)=1/3, x_(B)=2/3`
`500=1/3 p_(A)^(@)+2/3 p_(B)^(@)`
or `1500=p_(A)^(@)+2p_(B)^(@)` ...(i)
On adding 1 mole of B,
`p=525` mm Hg, `x_(A)=1/4, " " x_(B)=3/4`
`525=1/4 p_(A)^(@)+3/4p_(B)^(@)`
SUBTRACTING (i) from (ii)
`:.600 = p_(B)^(@)`
`:.1500=p_(A)^(@)+2xx600`
`:.p_(A)^(@)=300` mm Hg
Discussion
91643.

(a) 30 g of urea (M = 60 g "mol"^(-1)) is dissolved in 846 g of water. Calculate the vapour pressureof water for this solution if vapour pressure of pure water at 298 K is 23.8 mmHg. (b) Write two differences between ideal solutions and non-ideal solutions.

Answer»

SOLUTION :v.p.= 23.55 MM
Discussion
91644.

(A) 3-Oxo butanoic acid changes to propanone on heating with soda lime. (R) A mixture of NaOH and CaO is decarboxylating agent.

Answer»

Both A & R are true , R is the CORRECT EXPLANATION of A
Both A & R are true , R is not correct explanation of A
A is true , R is FALSE
A is false , R is true

Answer :A
Discussion
91645.

(A) +3 oxidation states is characteristic property of lanthanoids but cerium shows + 4 state also (R) Cerium acquire 4f^0 configuration after loosing one more eletron.

Answer»

Both (A) and (R) are TRUE and (R) is the CORRECT EXPLANATION of (A)
Both (A) and (R) are true and (R) is not the correct explanation of (A)
(A) is true but (R) is FALSE
Both (A) and (R) are false

Solution :Both (A) and (R) are true and (R) is the correct explanation of (A)
Discussion
91646.

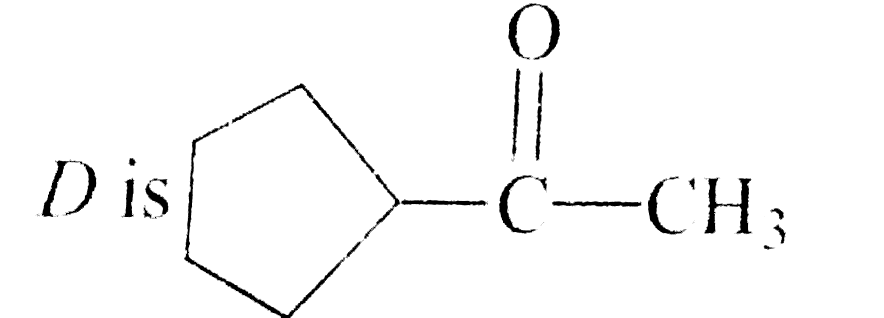
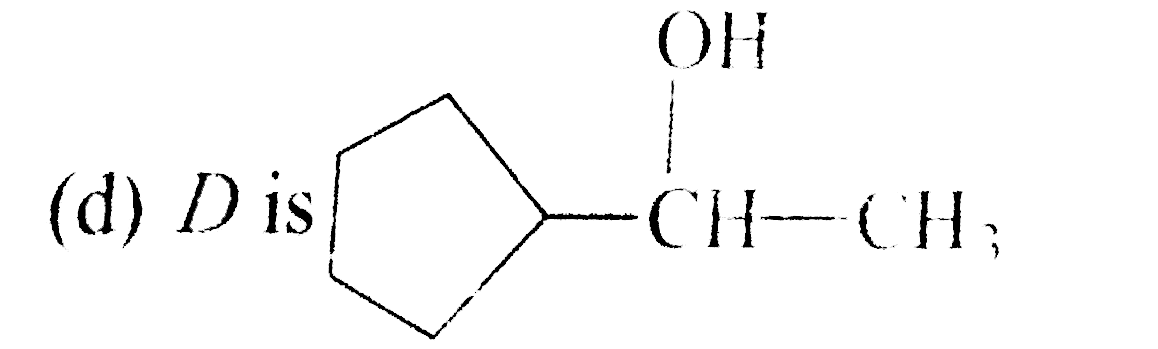
A 3^(@) optically active alcohol C_(9)H_(18)O 'A' on dehydration with conc. H_(2)SO_(4) produces B(C_(9)H_(16)) which exists in two stereoisomeric forms. For ozonolysis of B followed by work up with Zn-H_(2)O produces CH_(3)-underset(O)underset(||)(C)-H and C(C_(7)H_(12)O. C on treatment with LiAlH_(4) produces D(C_(7)H_(14)O). D on hehydration produced Identify the correct the correct answers.

Answer»




ANSWER :B::D
Discussion
91647.

A 2p-orbital has the following node/nodes:

Answer»

2 spherical
1 spherical
1 planar
1 planar and 1 spherical

Solution :2P has only ONE planar NODE.
Discussion
91648.

(A)+2C overset(2000^(@)C "to") underset(2500^(@)C) rarr (B)+2CO uarr (B) +"Carbon" overset(2000^(@)C" to ")underset(2500^(@)C) rarr ( C) If A is an example of 3-D silicate then select the correct statements about ( C).

Answer»

Central atom of C is `sp^(3)` hybridised
( C) is non-planar and all atoms are `sp^(3)` hybridised
( C) has diamond like structure, and it is colourless when impurity is present butyellow SOLID at ROOM temperature
( C) is silicon CARBIDE (SiC) and it is not being AFFECTED by any acid EXCEPT `H_(3)PO_(4)`

Answer :A::B::C::D
Discussion
91649.

(A): Reaction given below is possible 2KCI + Br_2 to Cl_(2) + 2KBr (R): lighter halogen displaces larger halogen from its metal halides .

Answer»

Both (A) and (R ) are true and (R ) is the correct explanation of (A)
Both (A) and (R ) are true and (R ) is not the correct explanation of (A)
(A) is true but (R ) is false
Both (A) and (R ) are false

ANSWER :D
Discussion
91650.

A + 2Bto3C + 2D The rate of disappearance of B is 1xx 10^(–2) "mol L"^(–1) "sec"^(–1). What will be(i) rate of reaction (ii) rate of change in the concentration of A and C ?

Answer»

Solution :`(5XX10^(-3),5xx10^(-3), 15xx10^(-3))ML^(-1)"SEC"^(-1)`
Discussion