InterviewSolution
Saved Bookmarks
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 1101. |
Find the sum: (i) (4-(1)/(n))+(4-(2)/(n))+(4-(3)/(n))+…up to n terms (ii) (a-b)/(a+b)+(3a-2b)/(a+b)+(5a-3b)/(a+b)+…….to20 terms |
|
Answer» |
|
| 1102. |
Draw the graph of the equation x+2y=4 and 3x + 6y =12. What do you observe ? How manny solutions do the equation have ? Write your conclusion. |
|
Answer» The equations have infinite SOLUTION. When two equations are GIVEN but the graph is only line, the equations will have infinitesolutions. |
|
| 1103. |
A ball is thrown vertically upwards from the top of a building of height 29.4m and with an initial velocity 24.5 m/sec. If the height H of the ball from the ground level is given by H = 29.4 + 24.5t - 4.9t^(2), then find the time taken by the ball to reach the ground. |
|
Answer» |
|
| 1104. |
From a right circular cylinder with height 10cmand radius of base 6cm, a right circular cone of the same height and base isremoved. Find the volume of the remaining solid. |
|
Answer» |
|
| 1105. |
The volume of a cylinderical vessel is 448picm^(3) and its height is 7 cm. find the diameter of the base. |
|
Answer» |
|
| 1106. |
Directions: In each question, four words have been given, out of which three are alike in some manner and the fourth one is different. Choose out the odd one. |
| Answer» SOLUTION :All except August are odd months while August is even (Sth) months. | |
| 1107. |
In the following frequency distribution, find the median class. What is the value of mean height ? |
|
Answer» 155.625 `(3xx935)/(6)=156.25+2M` `2xx935=4xx156.25+8M` `1870=625+8M` `8M=1870-625=1245` `M=(1245)/(8)=155.625` Thus (a) is CORRECT option. |
|
| 1108. |
A man invests 20020rs in buying shares of N.V. 26rs at 10% premium. The dividend on the shares is 15% per annum. Calculate (i) the number of shares he buys (ii) the dividend he receives annually (iii) the rate of interest he gets on his money |
|
Answer» |
|
| 1109. |
A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in the figure. If the height of the cylinder is 10 cm and its base radius is 3.5 cm, find the total surface area of the article. |
|
Answer» |
|
| 1110. |
(i) If 2x + 1 is a factor of 2x^2+ ax- 3, find the value of a. (ii) Find the value of k, if 3x -4 is a factor of expression 3x^2+ 2x -k. |
|
Answer» |
|
| 1111. |
Solve for x the quadratic equation x^(2)-4x-8=0. Give your answer correct to three significant figures. |
|
Answer» |
|
| 1112. |
In which ratio the point (-1,6) divides the line segment joining the points (-3, 10) and (6, -8) ? |
|
Answer» |
|
| 1113. |
Determine if the points (1, 5), (2, 3) and (-2, -11) are collinear. |
|
Answer» |
|
| 1114. |
How many square metres of canvas will be required to make a conical tent 3 metre high so that a man 2 metre high may stand anywhre with in a radius opf 70 cm from the centre without stoping? Give hyour answwer to the nearest whole number. |
|
Answer» |
|
| 1115. |
At the foot of a mountain, the angle of its summit is 45^(@). After ascending 1000m towards the mountain up a slope of 30^(@) inclination, the angle of elevation is found to be 60^(@). Find the height of the mountain (sqrt3= 1.732) |
|
Answer» |
|
| 1116. |
Anna Patil (Thane, Maharashtra) supplied vacuum cleaner to a shopkeeper in Vasal (Mumbai) for the taxable value of 14,000, and GST rate of 28%. Shopkeeper sold it to the customer at the same GST rate for 16,800 (taxable value). Find the following: What is CGST and SGST payable by shopkeeper in Vasai at the time of filing the return. |
|
Answer» |
|
| 1118. |
Anna Patil (Thane, Maharashtra) supplied vacuum cleaner to a shopkeeper in Vasal (Mumbai) for the taxable value of 14,000, and GST rate of 28%. Shopkeeper sold it to the customer at the same GST rate for 16,800 (taxable value). Find the following: Amount of CGST and SGST shown in the tax invoice issued by Annu Patil. |
|
Answer» |
|
| 1119. |
Anna Patil (Thane, Maharashtra) supplied vacuum cleaner to a shopkeeper in Vasal (Mumbai) for the taxable value of 14,000, and GST rate of 28%. Shopkeeper sold it to the customer at the same GST rate for 16,800 (taxable value). Find the following: Amount of CGST and SGST charged by the shopkeeper in Vasai. |
|
Answer» |
|
| 1120. |
Directions: In each question, four numbers are given out of which three are alike in same manner white one is different. Choose the odd one out. |
|
Answer» 125 |
|
| 1121. |
Construct a rectangle of 12.8 cm and 5 cmand then construct a square of area of the drawn rectangle and also find the length of each sides of those squares. |
|
Answer» |
|
| 1122. |
Use Euclid's division algorithm to find the HCF of following numben : (a) 65 and 111 (b)237 and 81 (c ) 55 and 210(d) 305 and 793 |
|
Answer» |
|
| 1123. |
Delta ABC has sides of length 5 cm, 6 cm and 7 cm. The perimeter of Delta DEF is 360 cm. If Delta ABC ~= Delta DEF then the ratio of the ratio of the perimeters of Delta ABC and Delta DEF is : |
|
Answer» `1 : 2` |
|
| 1124. |
Solve each of the following pairs of equations by reducing them to a pair of linear equations. (10)/(x+y)+(2)/(x-y)=4 and (15)/(x+y)-(5)/(x-y)=-2 |
|
Answer» |
|
| 1125. |
A cylindrical container with internal radius of its base 10 cm, contains water up to a height of 7 cm. Find the area of the wet surface of the cylinder. |
|
Answer» |
|
| 1126. |
Draw circles with centres A,B and C each of radius 3 cm, such that each circle touches the other two circles. |
| Answer» | |
| 1127. |
Solve the following pair of equations. 2/x+3/y = 13 |
|
Answer» `1/y = q = 3 => y=`1/3` |
|
| 1128. |
Evaluate the (tan^(2) 60^(@) + 4 cos^(2) 45^(@) + 3 sec^(2) 30^(@) + 5 cos^(2) 90^(@))/("cosec" 30^(@) + sec 60^(@) - cot^(2) 30^(@) ) |
|
Answer» |
|
| 1129. |
Point P (0, k) on reflection in the origin is invariant. Write the value of k. |
|
Answer» |
|
| 1130. |
Construct Caley's table for the set B = {1,3,5,7,9} under multiplication modulo 10. |
| Answer» | |
| 1131. |
Find the probability of getting a head when a coin is tossed once. |
|
Answer» |
|
| 1132. |
Yashscored 35 marks in a test, getting 2 marks for each right answer and losing 1 mark for each wrong answer. Had 3 marks been awarded for each correct answer and 2 marks been deduced for each incorrect answer, then Yash would have scored 50 marks. How many question were there in the test ? |
|
Answer» |
|
| 1133. |
If sec theta-tantheta=Pthen obtain the values of tan thetasecthetaand sinthetain terms of P. |
|
Answer» <P> |
|
| 1134. |
Which one of the following figures shows the quadratic equation ax^(2) + bx + c = 0 (a ne 0) having distinct roots? |
|
Answer»
|
|
| 1135. |
How mnay squares are there in the given figure? |
|
Answer» 6 |
|
| 1136. |
Rate of GST on essential commodities is ..... |
|
Answer» 0.05 |
|
| 1137. |
If the median of 60 observations, given below is 28.5, find the values of x and y. |
|
Answer» |
|
| 1138. |
Find the 10th term of an arithmetic progression whose first term is 'd' and common difference is 'b'. |
|
Answer» |
|
| 1139. |
The mid-points D, E, F of the sides of a triangle ABC are (3, 4), (8, 9) and (6, 7). Find the coordinates of the vertices of the triangle. |
|
Answer» |
|
| 1140. |
Find K, so that x^(2)+2x+K is a factor of 2x^(4)+x^(3)-14x^(2)+5x+6 . Also find all the zeros of the two polynomials. |
|
Answer» We get `(7k+21)x+2k^(2)+8k+6` as remainder is zero. `=> 7k+21=0` and `2k^(2)+8k+6=0` `=> k=-3` and `k=-1` or `-3` `=>k=-3` Zeros of `x^(2)+2x-3` are `1`, `-3` and `2x^(4)+x^(3)-14x^(2)+5x+6` are `1`, `-3`, `2`, `-(1)/(2)` |
|
| 1141. |
Solve each the following pairs of equations by reducing them to a pair of linear equations. (v) 5/x + y - 2/x-y =-1 15/x+y + 7/x-y = 10 |
|
Answer» |
|
| 1142. |
A motor boat whose speed is 18 km/h in still water. It takes 1 hour more to go 24 km upstream than to return downstream to the same spot. Find the speed of the stream. |
|
Answer» |
|
| 1144. |
A room in the form of a cylinder surmounted by a hemishperical vaulted dome contains 17.7m^(3) of air, and the internal diameter of the building is equal to the height of the dome above the floor. Find the height of the building. |
|
Answer» |
|
| 1145. |
Count the number of rectangles in the following figure. |
|
Answer» 8 |
|
| 1146. |
Find the roots of 3x^(2)-5x+2=0 by the method of completing the square. |
|
Answer» |
|
| 1147. |
Rahul an engieering student, prepared a model shaped like a cylinder with two cones attached at its ens. The diameter of the model is 3 cm and its length is 12 cm .If each conical part has a model (assume the oute and inner dimensions of the model to be nearly the same ),(ii) cost of painting the outer surface of the model at ₹ 12. 50 per cm^2 |
|
Answer» SOLUTION :Radius of each conical part `r = 3//2 cm ` Radius of CYLINDRICAL part , `r = 3//2 cm ` 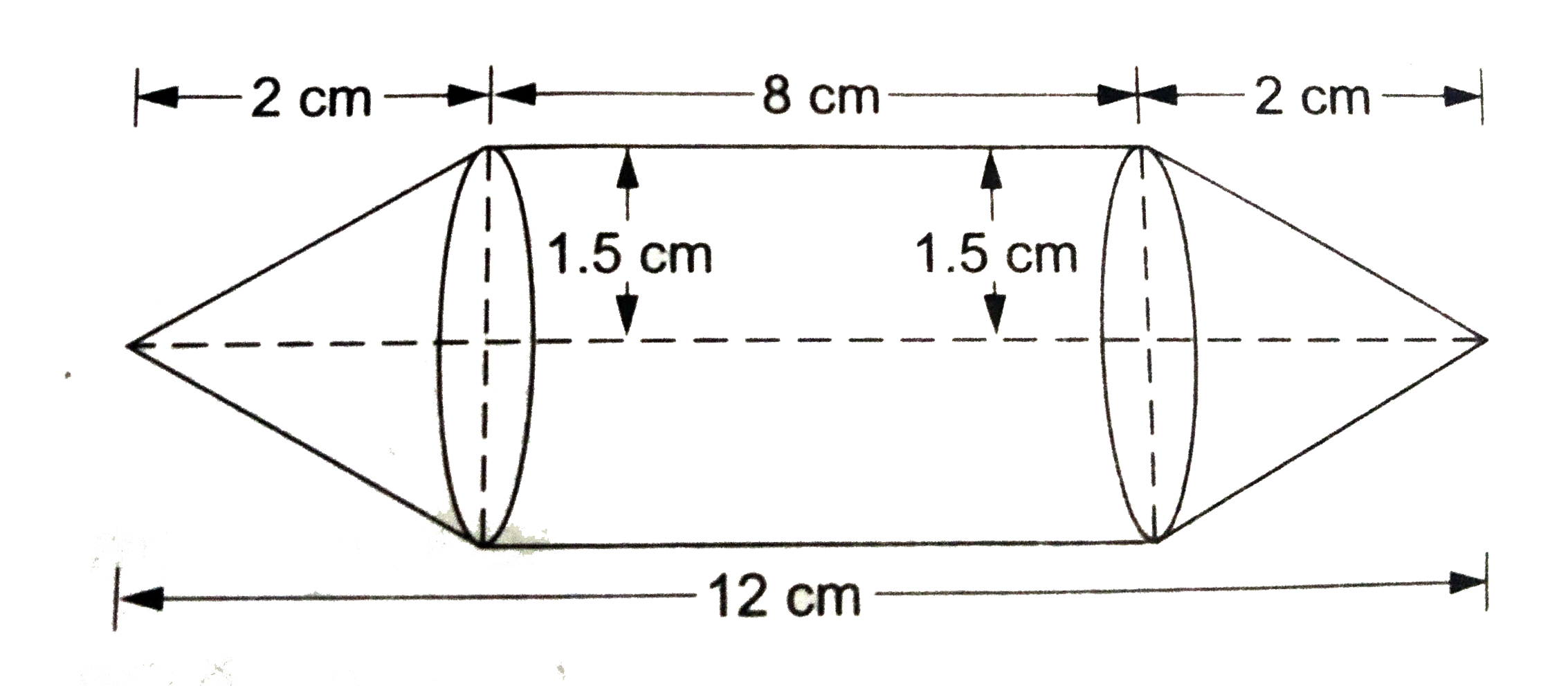 Height of each conical part, h=2cm Length of the cylinder part, `H= (12-2 xx 2 ) cm = 8 cm ` SLANT height of each conical part, `l= sqrt(r^2+ h^2)= sqrt((3/2)^2+2^2 cm = sqrt(9/4 + 4 ) cm ` `= sqrt(25/4) ` cm = 5/2 cm (i) Volume of air CONTAINED in the model = volume of 2 conical parts + volume of the cylindrical part `= 2 xx 1/3 pi r^2 h+ pi r^2H = pi r^2 (2/3 h+H)` `= [ 22/7 xx 3/2 xx 3/2 xx (2/3 xx 2 + 8 )] cm^3` `= (22/7 xx 3/2xx 3/2 xx 28/3)cm^2= 66 cm ^3` (ii) Total surface area of the model = curved SUFACE area of 2 conical parts + curved surface area of the cylindrical part `= 2 xx pirl + 2 pi r H = 2 pi rl (l+H)` `[2xx 22/7xx 3/2 xx (2.5 + 8)] cm^2` `= (2xx 22/7 xx 3/2 xx 10.5 ) cm^2 = 99 cm^2` `therefore` cost of painting the model = ₹` (99 xx 12.50) ` = ₹ 1237. 50 . |
|
| 1148. |
The lower part of a tent isa right circular cylinder of radius14 metres and itsupper part is a right circular cone . If the height of the cylindrical part is 3 metre and the total height of theper square- metre |
|
Answer» Solution :The radius of the CYLINDRICAL part = 14 m and the height of this part = 3 m ` :.` the curved SURFACE area of thecylindrical part ` = 2 xx 22/7 xx 14 xx 3 `, = 264 square - metre Again , the height of the CONICAL part OFTHE tent` = (13.5 -3) ` m = 10.5 m and the radius of base = 14 metre ` :. ` the slant height of the conical part ` = sqrt((14)^(2) + (10.5)^(2))`metre ` = sqrt(196 + 110.25 )`metre, ` = sqrt(306.250)` metre = 17.5metre ` :.` the curved surface area of the conical part of the tent ` = 22/7 xx 14 xx 17.5 ` sq - metre = 770 square - metre `:.` the areaof the part of the tent which is to be coloured = `(770+64) `square - metre = 1034 square - metre So the expenditure of COLOURING` = Rs 2 xx 1034` = Rs 2068 Hence the required expenditure = Rs 2068 
|
|
| 1149. |
To divide a line segment AB in the ration 4:7, a ray AX is first drawn such that BAX is an acute angle and then points A_1, A_2, A_3 , … located at equal distance on the ray AX and the point B is joined to |
|
Answer» 1)`A_12` |
|
| 1150. |
Complete thetable : {:("Point","Transformation ","Image"),((4,-8), .....................,(-4,-8)):} |
|
Answer» |
|