InterviewSolution
Saved Bookmarks
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 2801. |
Draw a circle of radius 3 cm. Take two points P and Q on one of its extended diameter each at a distance of 7 cm from its centre. Drew tangents to the circle from these two points P and Q. |
|
Answer» Solution :Given, two points P and Q on the diameter of a circle with rasius 3 cm. and OP = OQ = 7 cm We have to construct the tangents to the circle from the given points P and Q. Steps of Construction : 1. DRAW a circle of radius 3 cm with centre at O. 2. Produce its diameter on both sides and take points P and Q on diameter such that OP - OQ = 7 cm, 3. BISECT OP and OQ. Let E and F be the mid-points of OP and OQ, respectively. 4. Take E as centre and OE as radius draw a circle which interect the given circle (0,3) at two points M and N. Again, taking F as centre and OF as radius draw a circle which intersect the given circle (0,3) at two points P' and Q' 5. Join PM, PN, QP' and QQ'. These are the required tangents from P and Q to the given, circle (0,3). Justifiction : Join OM and ON. The `angleOMP` is the angle lies in the semi-circle and therefore `angleOMP=90^(@).` Since, OM is radium of the circle. So, MP has to be tangent to the circle. Similarly PN, QP' and QQ' are also tangents to the given circle. 
|
|
| 2802. |
Mr. Mayur's(age 47 years) annual income is Rs. 4,00,000 . If he does not have any savings by which he can claim duductions from his income. Then find the amount on which education cess will be levied. |
|
Answer» |
|
| 2803. |
The zeroes of the cubic polynomial x^(3)-6x^(2)+3x+10 are in A.P. for some real numbers a and d. Find the zeroes of the gives polynomial. |
|
Answer» |
|
| 2805. |
A cylindrical beaker, whose base has a radius of 15 cm, is filled with water up to a height of 20 cm. A heavy iron spherical ball of radius 10 cm is dropped to submerge completely in water in the beaker. Find the increase in the level of water. |
|
Answer» |
|
| 2806. |
Which of the following are sets? Justify your answer (i) The collection of all the months of a year begimng with the letter "J". (ii) The collection of ten most talented writers of India. (iii) A team of eleven best cricket batsmen of the world. (iv) The collectionofall boys in your class. (v) The collection of all even integers. |
|
Answer» |
|
| 2807. |
IF x=root3(sqrt2+1)-root3(sqrt2-1) then x^2+3x=………… |
|
Answer» 1 |
|
| 2808. |
By investing 45000rs in 10% 100rs shares, Shared gets 3000rs as dividend. Find the market value of each share. |
|
Answer» |
|
| 2809. |
If they are in G.P.Write next one terms. 1/2, 1/4, 1/6,……. |
| Answer» | |
| 2810. |
Write first four terms of the AP, when the first term a and the common difference d are given as follows: (i) a=10, d=10 (ii) a=-2, d=0 (iii) a=4, d=-3 (iv) a=-1, d=1/2 (v) a=-1.25, d= -0.25 |
|
Answer» (iii) 4,1,`-2,-5`, (IV) `-1,-1/2,0,1/2` (V) `-1.25, -1.5, -1.75, -2` |
|
| 2811. |
Which term of the A.P. 4.2, 4.7,5.2,5.7….. Is 8.7? |
|
Answer» |
|
| 2812. |
The shape of solid iron rod is cylinderical Its height is 11 cm and base diameteris 7 cm Then find the total volume of 50 such rods. |
|
Answer» |
|
| 2813. |
A tailor stiches trousers and shirts and each piece is completed by two machine I and II. To complete each trousers, machines I and IImust work 3/2 hours and 2 hours respectively, and to complete each shirt, machines I and II must work 2 hours and 1 hours respectively Machine I may not operate for more than 12 hours ped day and machine II not more than 11 hours per day. If the profit on each trouser and eachshirt is Rs. 150 and Rs. 100 repectively, then the maximum profit is _______ |
|
Answer» RS. 900 Let the number of shirts=y 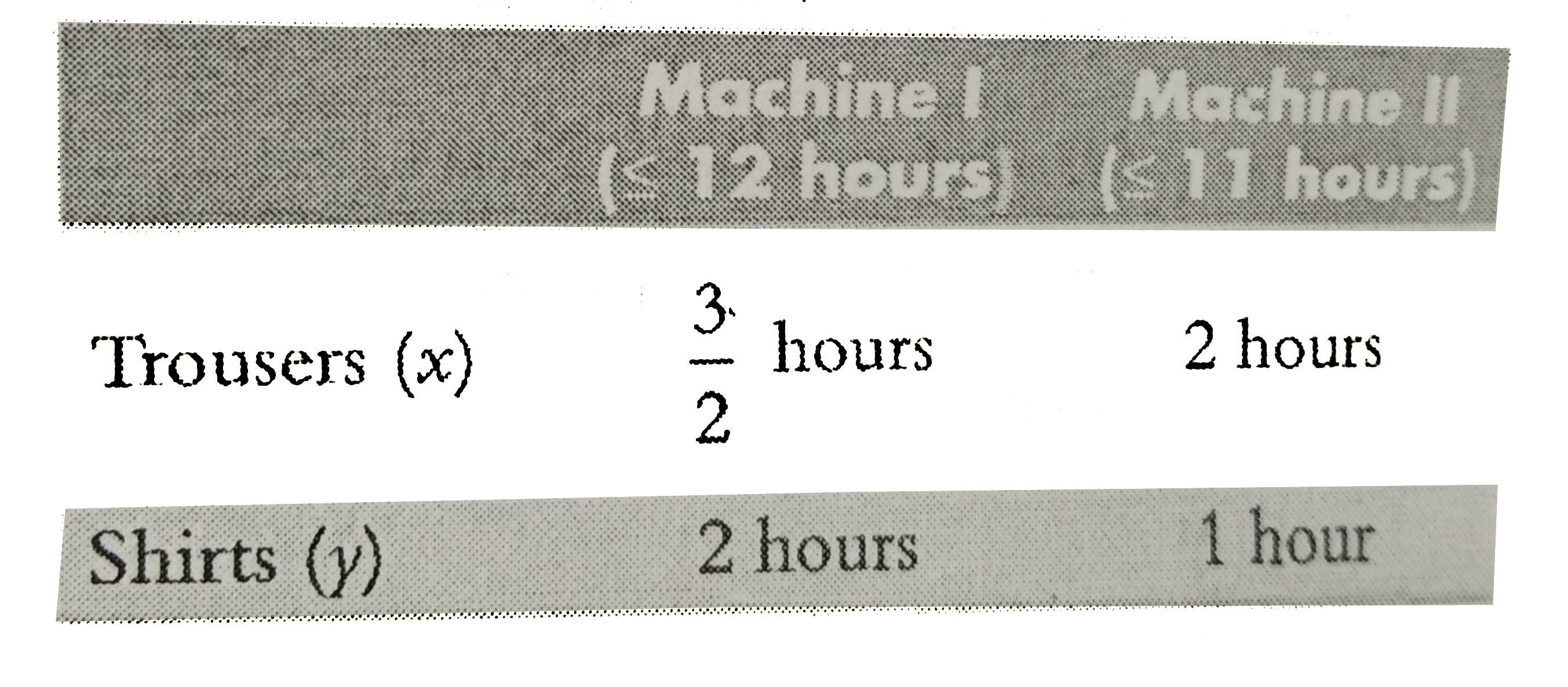 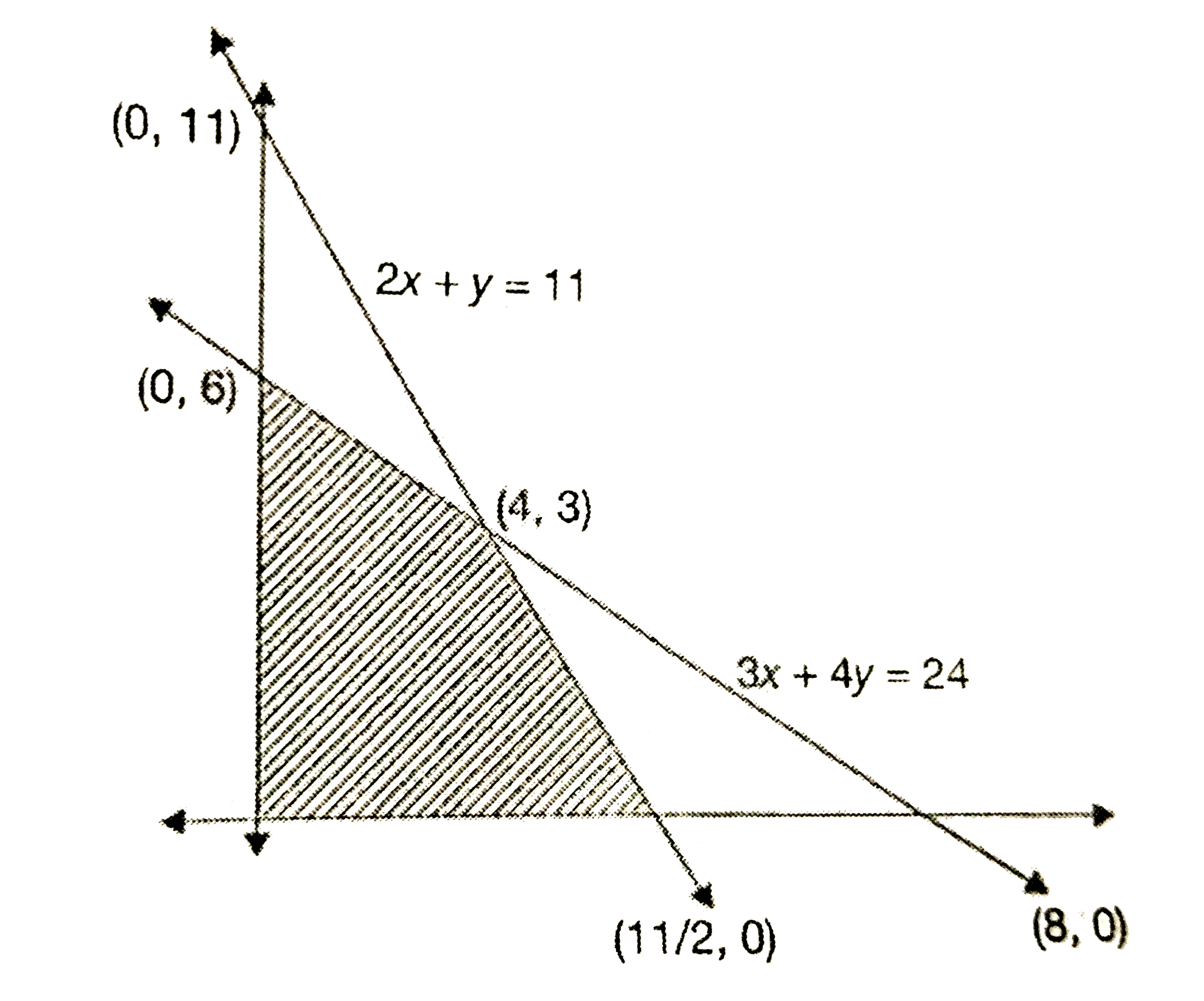 According to the given condition : `implies (3x)/(2)+2y LE 12 and 2x+y le 11` `implies 3x+4y le24 and 2x+y le 11` `x ge 0, y ge 0` The profit function , p=15x+10y The shaded region is a closed- convex polygon with vertices `((11)/(2),0),(4,3),(0,6),(0,0).` `:.` ABCD is the feasible reason. `:.` THe maximum profit is at C(4,3), i.e., `P=150xx4+100xx3=900.` |
|
| 2814. |
In which of the following situations, does the list of numbers involved form an arithmetic progression, and why? (i)The taxi fare after each km when the fare is Rs 15 for the first km and Rs 8 for additional km. (ii) The amount of air present in a cylinder when a vacuum pump removes (1/4)^(th) of the air remaining in the cylinder at a time. (iii)The cost of digging a well, after every metre of digging, when it costs 150 for the first metre and rises by 50 for each subsequent metre. (iv)The amount of money in the account every year, when 10000 is deposited at compound interest at 8 % per annum. |
|
Answer» |
|
| 2815. |
If the median of the distribution given below is 28.5. Find the values of x and y. |
|
Answer» |
|
| 2816. |
Which of the following squences are A.P.? If they are A.P. find the common difference -10, -6, -2, 2,… |
|
Answer» (ii) AP, next three terms =4 `,9/2, 5` (iii) AP, next three terms `=-9.2, -11.2, -13.2` (iv) AP, next three terms =6,10,14 (V) AP, next three terms `=3+4sqrt(2), 3+5sqrt(2), 3+6sqrt(2)` (vi) Not AP (vii) AP, nesxt three terms `=-16, -20, -24` (viii) AP, next three terms `=-1/2, -1/2, -1/2` (ix) Not AP (x) AP, next three term = 5a, 6a, 7a (xi) Not AP (xii) AP, next three terms `=sqrt(50), sqrt(72), sqrt(96)` (xiii) Not AP |
|
| 2817. |
If sin 3A = cos (A - 26^@), where 3A is an acute angle, then find the value of A. |
|
Answer» |
|
| 2818. |
If the co - ordinates of the mid points of DeltaABC are D(1, 2) E(0, -1) and F(2, -1). Find the respective co - ordinates of DeltaABC. OR Find the length of the median through the vertex A(5, 1) drawn to the triangle ABC where other two vertices are B(1, 5) and C(-3, -1) |
|
Answer» `B(x_(2)y_(2))=B(0, -1)` `C(x_(3)y_(3))=C(0, -1)` OR `:.` Length of MEDIAN `= sqrt(37)` |
|
| 2819. |
True or False: A pair of tangents can be constructed to a circle of radius 4 cm from a point P situated at a distance 8 cm from the centre. |
|
Answer» |
|
| 2820. |
Find the values of k for each of thequadratic equations, so that they have two equal roots. kx(x-2)+6=0 (k ne 0) |
|
Answer» |
|
| 2821. |
Prove that sin^(8)theta-cos^(8)theta=cos2theta(2sin^(2)thetacos^(2)theta-1). |
| Answer» | |
| 2822. |
If A=[{:(,2,1),(,1,3):}] and B=[ {:(, 3),(,-11 ):}] . find the matrix X such that AX=B. |
|
Answer» |
|
| 2823. |
In figure O is any point inside a rectangle ABCD. Prove that OB^(2)+OD^(2)=OA^(2)+OC^(2). |
|
Answer» |
|
| 2824. |
Draw a pair of tangents to a circle of radius 5 cm which are inclined to each other angle of 60^(@). |
|
Answer» Solution :Steps of construction : 1. Take a point O on the plane of the paper and draw a circle with centre O and radius oA=5cm. 2. At O construct radii OA and OB such that to `angleAOB` equal `120^(@)` i.e., supplement of the angle between the tangents. 3. Draw PERPENDICULAR to OA and OB at A and B RESPECTIVELY SUPPOSE these perpendicular intesect at P. Then, PA and PB are REQUIRED tangents. 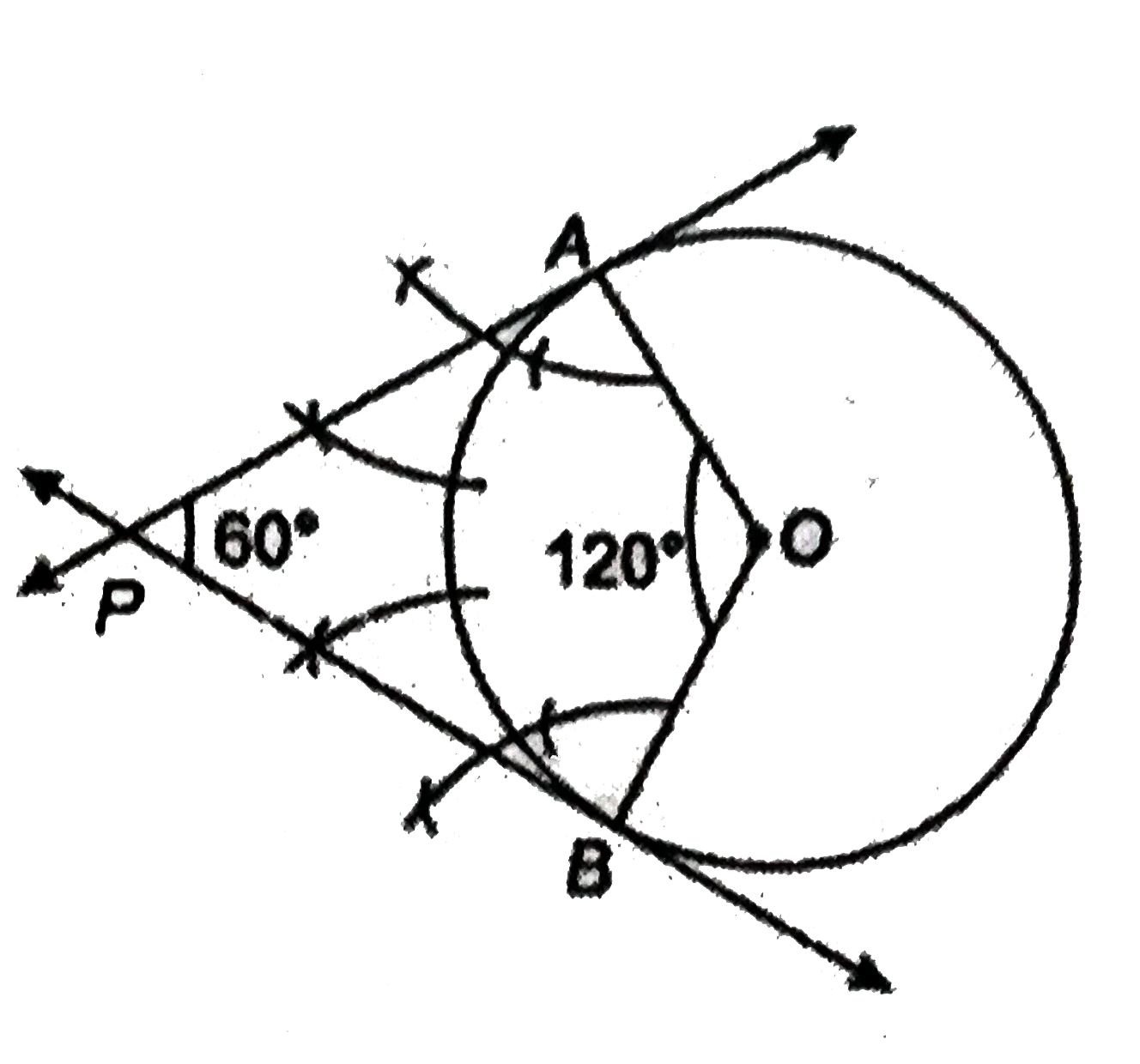
|
|
| 2825. |
If the radius of the circle is 6 cm and the length of an arc is 12 cm. Find the area of the sector. |
|
Answer» |
|
| 2826. |
" B is the set of all months in a year having 30 days". Write in roster form. |
|
Answer» B={APRIL, May , June, September, November} |
|
| 2827. |
Find a relation between x and y if the prints A(x, y), B(-4, 6) and C(-2, 3) are collinear. |
|
Answer» |
|
| 2828. |
Solve the equation : (5)/(2-x)+(x-5)/(x+2)+(3x+8)/(x^(2)-4)=0 |
|
Answer» SOLUTION :We have, `(5)/(2-X)+(x-5)/(x+2)+(3x+8)/(x^(2)-4)=0` `implies(5(x+2)+(2-x)(x-5))/((2-x)(x+2))-(3x+8)/((2+x)(2-x))=0` `implies(5x+10+2x-10-x^(2)+5x-3x-8)/((2-x)(2+x))=0` `implies-x^(2)+9x-8=0impliesx^(2)-9x+8=0` `implies(x-1)(x-8)=0` `:.x=1orx=8` |
|
| 2830. |
Find the sum of: (i) the first 1000 natural numbers, (ii) the first n natural numbers. |
|
Answer» (II) `S_(N) = (n(n+1))/2` |
|
| 2831. |
If the mean of x_(1) and x_2is M_1 and that of x_1,x_2, x_3, x_4is M_2 , the mean of x_(1),x_(2)//a,x_(3)+a,x_(4)-ais |
|
Answer» `M_2+((a-1)(x_1-2M_1))/(4A)` |
|
| 2832. |
A card is drawn from a well shuffled deck of playing cards. Find the probability of getting the spade card. Also find the probability that the card is not king . |
|
Answer» |
|
| 2833. |
Solve the followingsimultaneous equations : 49x - 57 y = 172 ,57 x - 49 y = 252 |
|
Answer» |
|
| 2835. |
I. P + Q means P is mother of Q. II. PdivQ means P is father of Q. III. P - Q means P is sister of Q. Which of the following shows that M is daughter of R? |
|
Answer» `RdivM+N` |
|
| 2836. |
A man invests 8800rs in buying shares of a company of face value of rupees hundred each at a premium of 10%. If he earns 1200rs at the end of the year as dividend, find : (i) the number of shares he has in the company (ii) the dividend percent per share. |
|
Answer» |
|
| 2837. |
What is the probability of getting atmost one tail when two coins are tossed simultaneously? |
|
Answer» |
|
| 2838. |
Prove that : sqrt((1+sinA)/(1-sinA))-sqrt((1-sinA)/(1+sinA))=2tanA |
|
Answer» |
|
| 2839. |
Student of a school are standing in rows and columns in their playground for a drill practice. A, B, C, D are the positions of four students as shown in the figure. Is it possible to place Jaspal in the drill in such a way that he is equidistant from eachl of the four students A, B, C and D? Ifso, what should be his position ? |
|
Answer» Solution :Co-ordinates of A, B, C and D fron graph are A(3, 5), B(7, 9), C(11, 5) and D(7, 1). To find the shape of `SQUAREABCD` : `""AB^(2)=(7-3)^(2)+(9-5)^(2)=4^(2)+4^(2)=32` `rArr""AB=4sqrt(2)` units `""BC^(2)=(11-7)^(2)+(5-9)^(2)=(4)^(2)+(-4)^(2)=32` `rArr""BC=4sqrt(2)` units `""CD^(2)=(7-11)^(2)+(1-5)^(2)=(-4)^(2)+(-4)^(2)=32` `rArr""CD=4sqrt(2)` units `""DA^(2)=(7-3)^(2)+(1-5)^(2)=4^(2)+(-4)^(2)=32` `rArr""DA=sqrt(4^(2)(1+1))=4sqrt(2)` units `therefore""AB=BC=CD=DA=4sqrt(2)` units So, ABCD will be EITHER square or rhombus. Now, `"""DIAGONAL "AC=sqrt((11-3)^(2)+(5-5)^(2))` `rArr""AC=sqrt((8)^(2)+(0)^(2))""rArrAC=8` units and `"""diagonal "BD=sqrt((7-7)^(2)+(1-9)^(2))=sqrt((0)^(2)+(-8)^(2))=sqrt(8^(2))` `rArr""BD=8` units `therefore """Diagonal "AC="Diagonal "BD` So, given quadrilateral ABCD is a squre. The point which is equidistant from point A, B, C, D of a square ABCD will be at the intersecting point of diagonals and diagonals bisects each other. Hence, the required point O equidistant from A, B, C, D is mid-point of any diagonal `=((7+7)/(2), (9+1)/(2))=((14)/(2), (10)/(2))=(7, 5)`. Hence, the required point is (7, 5). |
|
| 2840. |
Choose the diagrams which represent the body, girl and a dog. |
|
Answer»
|
|
| 2841. |
IF E_(1)E_(2) E_(3 )"…….." E_(10)are thepossibleelementaryeventsofarandomexperiment , then P(E_1) +P(E_2) +P(E_3) +"……"P(E_(10)) isequalto |
|
Answer» 0 |
|
| 2842. |
A dice is rolled two times or two dice are rolled together. Find the probability of getting: (iii) a composite number on each dice. |
|
Answer» |
|
| 2843. |
A man invests equal amounts of money in two companies A and B. Company A pays a dividend of 15% and its Rs100 shares are available at 20% discount. The shares of company B has a nominal value of Rs25 and are available at 20% premium. If at the end of one year, the man gets equal dividends from both the companies, find the rate of dividend paid by company B. |
|
Answer» |
|
| 2844. |
From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of circle is : |
|
Answer» 7 cm |
|
| 2845. |
Find the roots of the following quadratic equations, if they exist by the method of completing the square. (i) 2x^(2)-7x+3=0 (ii) 4x^(2)+4sqrt3x+3=0 |
|
Answer» Solution :Given equation is `2x^(2)-7x+3=0` DIVIDING both sides by 2 `X^(2)-(7)/(2)x+(3)/(2)=0` ADDING `(("COEFFICIENT of x")/(2))^(2)"""on both sides,i.e.,"((7)/(2)xx(1)/(2))^(2)=(49)/(16)` `x^(2)-(7)/(2)x+(49)/(16)=(-3)/(2)+(49)/(16)` `implies(x-(7)/(4))^(2)=((5)/(4))^(2)` `:.x-(7)/(4)+-(5)/(4)""(why?)` `impliesx=(7)/(4)+-(5)/(4)=(7+-5)/(4)` `impliesx=(12)/(4),(2)/(4)` `impliesx=3,(1)/(2)` Hence, roots of the equation are `(1)/(2)` and 3. (II) Given equation is `4x^(2)+4sqrt3x+3=0` Dividing both sides by 4 `impliesx^(2)+sqrt3x+(3)/(4)=0` `impliesx^(2)+sqrt3x=(3)/(4)` Adding `(("coefficient of x")/(2))^(2)i.e.,((sqrt3)/(2))=(3)/(4)"on both sides"` `x^(2)+sqrt3x+(3)/(4)=(-3)/(4)+(3)/(4)` `implies(x+(sqrt3)/(2))^(2)=0` `:.(x+(sqrt3)/(2))=0and((x+(sqrt3)/(2)=0` `impliesx=(-sqrt3)/(2)andx=(-sqrt3)/(2)` Hence, roots of the equation are `(-sqrt3)/(2)andx=(-sqrt3)/(2)` |
|
| 2846. |
Two circles C(0, r) and C'(0', r') touch externally at P(3, 1). If the co-ordinates of O and O' are (1, p) and (q, -2) repectively. Their areas are in the ratio 4 : 9. Find the value of p^(2)+q^(2). |
|
Answer» |
|
| 2848. |
Read the following information carefully and answer the questions given below it: The sum of the income A and B is more than of C and Dtogether .The sum of the income of A and Moreover,A earns half as much as the much of the income of B and D. Whose income is the highest? |
|
Answer» A |
|
| 2849. |
Read the following information carefully and answer the questions given below it: The sum of the income A and B is more than of C and Dtogether .The sum of the income of A and Moreover,A earns half as much as the much of the income of B and D. Which of the following statements is not correct? |
|
Answer» A earns more than B |
|
| 2850. |
A joker's cap is in the form of right circular cone whose base radius is 7 cm and heights is 24 cm . Find the area of the sheet required to make 10 such caps. |
|
Answer» |
|