InterviewSolution
Saved Bookmarks
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 3201. |
A company with 10000 shares of 100rs each declares an annual dividend of 5% (i) What is the total amount of dividend paid by the company ? (ii) What should be the annual income of man who has 72 shares in the company ? |
|
Answer» |
|
| 3202. |
Construct two circles of radii 2 cm and 3 cm, the distance between whose centres is 8.7 cm.Then draw a transverse common tangent to these two circles. |
Answer» Solution : Here, PQ is the required transverse COMMON TANGENT to the circles with CENTRES at O' and O. |
|
| 3203. |
If A = {0,1,2,3,4,5,6,7,8,9,10}, then list out all the pairs of distinct numbers from set A which are congruent to each other under modulo 5. |
|
Answer» |
|
| 3204. |
The mean wage of 150 labourers working in a factory running three shifts with 60, 40 and 50 labourers is Rs 114.00. The mean wage of 60 labourers working in the first shift is Rs 121.50 and that of 40 labourers working in the second shift is Rs 107.75, then the mean wage of those working in the third shift is |
| Answer» ANSWER :A | |
| 3205. |
Market value of sharesand dividend declared by the two companies is given below. Face value is same and it is 100 for both the shares. Investment in which company is more profitable? a. Company A -160, 15% b. Company B -225, 20% |
|
Answer» |
|
| 3206. |
A hemisphere is cut from one face of a cubical wooden block such that the diameter of the hemisphere is equal to the side of the cube. Determine the total surface area of the remaining solid. |
|
Answer» |
|
| 3207. |
A storage tank consists of a circular cylinder with a hemisphere stuck on either end. If the external diameter of the cylinder be 1.4 cm and its length be 8 m. Find the cost of painting it on the outside at rite of Rs. 20per m^2. |
|
Answer» |
|
| 3208. |
If t_(n) represents nth term of an A.P., t_(2)+t_(5)-t_(3)= 10 and t_2 + t_9= 17. find its first term and its common difference. |
|
Answer» |
|
| 3209. |
Find the corrdinates of the point which divides the join(-1, 7) and (4, -3) in the ratio 2:3. |
|
Answer» |
|
| 3210. |
A sphere , a cylinder and a cone are of the same radius and same height . Find the ratio of their curved surface areas. |
|
Answer» |
|
| 3211. |
Find the coordinates of centroid of the triangle with vertices: -1, 3), (6, -3) and (-3, 6) |
|
Answer» |
|
| 3212. |
Find the roots of the following quadraticequations by factorisation : x^(2)-3x-10=0 |
|
Answer» |
|
| 3213. |
If x+y+z=0, then (x^2)/( yz) + (y^2)/( zx) + (z^2)/( xy) is equal to |
|
Answer» 3 |
|
| 3214. |
Solve: (i) 8/(x+2y)+3/(2x-y)=3,12/(x+2y)-6/(2x-y)=1. (ii) 2/(x-1)+3/(y-2)=1,5/(x-1)+6/(y-2)=7 (iii) 1/(3x+y)+1/(3x-y)=12/35,1/(2x(3x+y))-1/(2(3x-y))=2/35 |
|
Answer» |
|
| 3215. |
Check whether the following equations are consistent or inconsistent. Solve them graphically. (c ) 3/2x + 5/3y = 7 9x - 10y = 12 |
|
Answer» |
|
| 3216. |
If the sum of the coefficients in the exapansion (4ax-1-3a^(2)x^(2))^(10) is 0, then the value of a can be __________ |
|
Answer» 2 |
|
| 3217. |
An A.P. consists of 50 terms of which 3rd term is 12 and the last term is 106. Find the 29th term of the A.P. |
|
Answer» |
|
| 3218. |
A point P is reflected in the origin. Co-ordinates of its image are (-2, 7). Find the co-ordinate of P. |
|
Answer» |
|
| 3219. |
8 men and 12 boys canfinish a piece of work in 10 days while 6 men and 8 boys can finish it in 14days. Find the time taken by one man alone and that by one boy alone tofinish the work. |
|
Answer» |
|
| 3221. |
Which one of the following diagrams correctly represents the relationship among the classes:Tennis fnas ,Cricket player,students? |
|
Answer»
|
|
| 3222. |
Find the radius of the circle whose centre is (3, 2) and passes through (-5, 6). |
|
Answer» |
|
| 3223. |
The vertices of a DeltaABC are A(3, 8), B(-1, 2) and C(6, 6). Find : (i) Slope of BC. (ii) Equation of a line perpendicular to BC and passing through A. |
|
Answer» |
|
| 3224. |
Find the roots of following quadratic equations by using quadratic formula, if they exist. (i)2x^(2)+x-4=0 (ii) 2x^(2)+x+4=0 (iii) 2x^(2)+5sqrt3x+6=0 (iv) sqrt3x^(2)+11x+6sqrt3=0 |
|
Answer» Solution :(i) GIVEN equation is `2x^(2)+x-4=0` ) On comparing with `ax^(2)+bx+c=0`, we get a=2,b=1 and c=-4 `:. "DISCRIMINAT", D=b^(2)-4ac` `impliesD=(1)^(2)-4xx2xx(-4)` `impliesD=1+32` `impliesD=33gt0` Hence, the given equation has two real roots. `:.x=(-b+-sqrtD)/(2a)` `impliesx=(-1+-sqrt33)/(4)` `impliesx=(-1+sqrt33)/(4),(-1-sqrt33)/(4)` are roots of to the equation. (ii) Give equation is `2x^(2)+x+4=0` On comparing with `ax^(2)+bx+c=0`, we get a=2, b=1 and c=4 `:."Discriminant",D=b^(2)-4ac` `impliesD=(1)^(2)-4xx2xx4` `impliesD=1-32` `impliesD=-31lt0` Hence, the equation has no real roots. (iii) Given equation is `2x^(2)+5sqrt3x+6=0` On comparing with `ax^(2)+bx+c=0`, we get `a=2,b=5sqrt3andc=6` `:."Discriminant"D=b^(2)-4ac` `impliesD=(5sqrt3)^(2)-4xx2xx6` `impliesD=75-48` `impliesD=27gt0` Hence, the equation has two real roots. `:.x=(-b+-sqrtD)/(2a)` `impliesx=(-5sqrt3+-sqrt27)/(4)impliesx=(-5sqrt3+-3sqrt3)/(4)` `impliesx=(-2sqrt3)/(2)and(-8sqrt3)/(4)` `impliesx=(-sqrt3)/(2)and-2sqrt3` are roots of the equation. (IV) Given equation is `sqrt3x^(2)+11x+6sqrt3=0` On comparing with `ax^(2)+bx+c=0` we get `a=sqrt3,b=11andc=6sqrt3` `:."Discriminant"D=b^(2)-4ac` `impliesD=11^(2)-4xxsqrt3xx6sqrt3` `impliesD=121-72` `impliesD=49gt0` Hence, the given equation has two real roots. `:.x=(-b+-sqrtD)/(2a)` `impliesx=(-11+-sqrt49)/(2sqrt3)impliesx=(-11+-7)/(2sqrt3)` `impliesx=(-11+7)/(2sqrt3)and(-11-7)/(2sqrt3)` `impliesx=(-4)/(2sqrt3)xx(sqrt3)/(sqrt3)and(-18)/(2sqrt3)xx(sqrt3)/(sqrt3)` `impliesx=(-4sqrt3)/(6)and(-18sqrt3)/(6)` `impliesx=(-2sqrt3)/(3)and-3sqrt3` are roots of the equation. |
|
| 3225. |
Without solving equation x^(2)-x+1=0, find whether x=-1 is a root of this equation or root. |
|
Answer» |
|
| 3226. |
Find the area of the shaded region where a circularare of Radius 6 cm has been drawn with the vertex 'O'of an equilateralTriangle OAB of side 12cm as centre. OR From each corner of a square ofside 4 cm a quadrant of a circle of radius 1cm is cut and also a circle of diameter 2 cm is cut as show in Fig, Find the area of the remaining portion of the square. |
|
Answer» OR `(68)/(7)` sqcms |
|
| 3227. |
One side of an equilateral triangle is 36 cm. The mid-points of its sides are joined to form another triangle. Again another triangle is formed by joining the mid-points of the sides of this triangle and the process is continued indefinitely. Determine the sum of areas of all such triangles including the given triangle. |
|
Answer» |
|
| 3228. |
P is a point in the plane of a circle with centre O and radius 4 cm. If OP = 3 cm, ..... tangent/s can be drawn to the circle from point P. |
|
Answer» |
|
| 3231. |
Construct a tangent to a circle of radius 4cm from a point on the concentric circle of radius 6cm and measure its lengths. Also Verify the measurement by actual calculation. |
|
Answer» LENGTH of TANGENT by measurement and actual calculation are same. |
|
| 3232. |
Draw a tangent to a given circle with center O from a point 'R' outside the circle. How many tangents can be drawn to the circle from that point ? |
|
Answer» |
|
| 3233. |
Neel has invested in shares as follows. Find his total investment. Company A : 350 shares, FV=10, premium =7 Company B : 2750 shares, FV=5, Discount =1 Company C : 50 shares, FV=100, MV=150 |
|
Answer» |
|
| 3234. |
If A=[{:(,3,x),(,0,1):}] and B=[{:(,9,16),(,0,-y):}] find x and y when A^2=B. |
|
Answer» |
|
| 3235. |
Length of the shadow of a person is x when the angle of elevation of the sun is 45°. If the length of the shadow increased by (sqrt(3)-1)x,then the angle of elevation becomes |
|
Answer» `15^(@)` |
|
| 3236. |
If the facevalue of both the shares is same, then which investment out of the following is more profitable? Company A: dividend 15%, MV=110, Company B: dividend 12%, MV=150. |
|
Answer» |
|
| 3237. |
Find the zeroes of the quadratic polynomial x^(2)+7x+10 and verify the relationship between its zeroes and coefficients. |
|
Answer» |
|
| 3238. |
Draw a circle of radius 4 cm. Take a poin P outside the circle. Without using the centre of the circle, draw two tangents to the circle from point P. |
|
Answer» Solution :Steps of Construction : 1. Draw a line segment 4 cm. 2. Take a point P outside the circle and draw a SECANT PAB, intersecting the circle at A and B. 3. Produce AP to C such that AP=CP. 4. Draw a semi- circle with CB as diameter. 5. Draw PD `bot` CB, intesecting the semi- circle at D. 6. With P as CENTRE and PD as RADIUS draw arcs to intersect the GIVEN circle at T and T'. 7. Join PT and PT'. Then, PT and PT' are the required tangents. 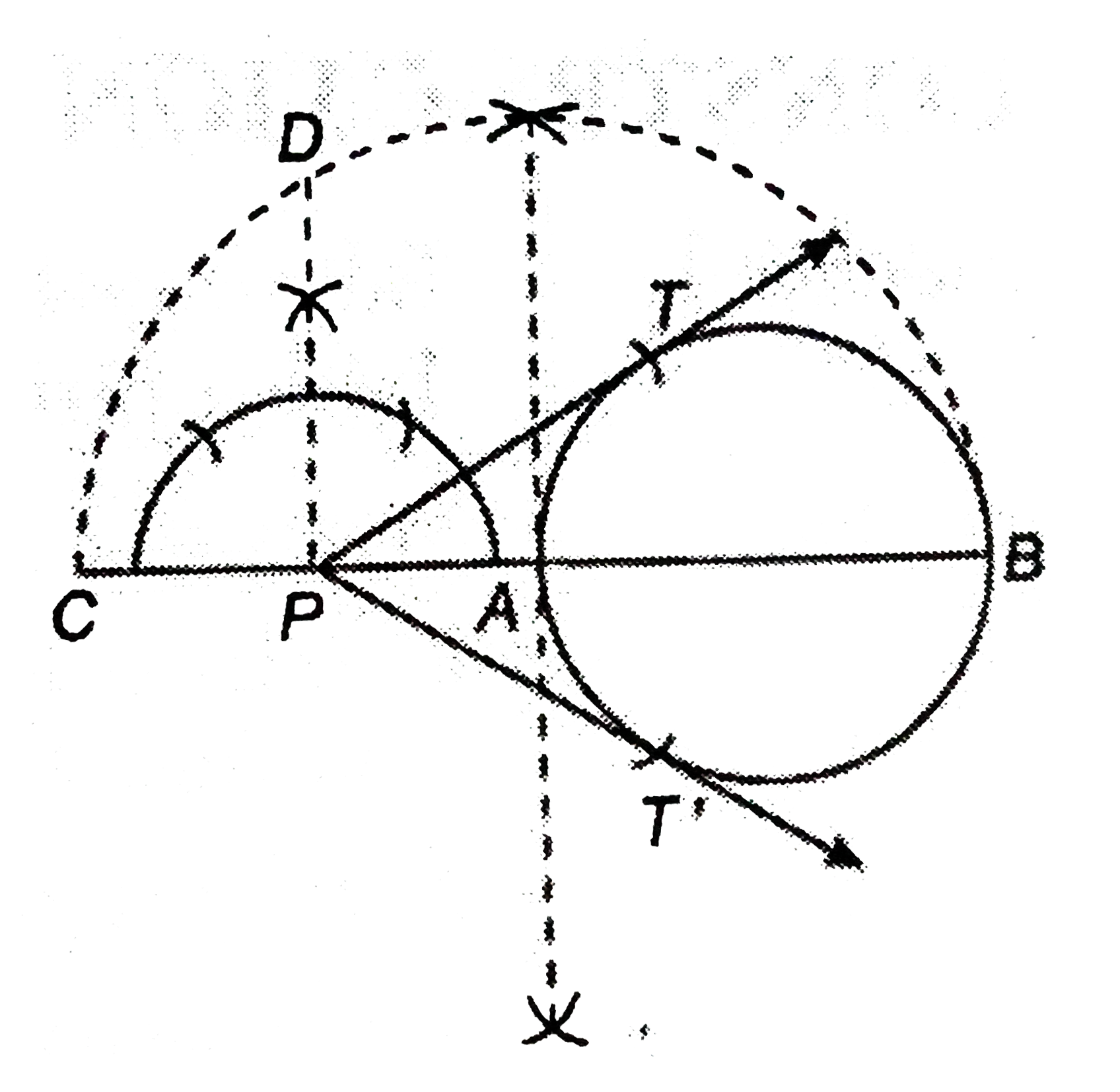
|
|
| 3239. |
Find x and y, if : (i) [{:(,4,3x),(,x,-2):}] [{:(,5),(,1):}]=[{:(,y,8):}] (ii) [{:(,x,0),(,-3,1):}] [{:(,1,1),(,0,y):}]=[{:(,2,2),(,-3,-2):}] |
|
Answer» |
|
| 3240. |
If the face value of both the shares is same, then which investment out of the following is more profitable? Company A : dividend 16%, MV=80, Company B : dividend 20%, MV=120. |
|
Answer» |
|
| 3241. |
Draw a tangent to the circle from the point P having radius 3.6 cm and centre at O. Point P is at a distance 7.2 cm from thecentre. |
|
Answer» |
|
| 3242. |
(i) A hemisphere of maximum possible diameter is placed over a cuboidal block of side 7 cm. Find the surface area of the solid so formed. (ii) A cubical block of side 10 cm is surmounted by a hemisphere. What is the largest diameter that the hemisphere can have ? Find the cost of painting the total surface area of the solid so formed, at the rate of Rs. per 100 sq cm. [Use pi=3.14.] |
|
Answer» |
|
| 3243. |
Draw a circle of radius 3 cm. From a point P, 7 cm away from its centre, draw two tangents to the circle. Measure the length of each tangent. |
|
Answer» |
|
| 3244. |
Determine the AP whose third term is 16 and the 7th term exceeds the 5th term by 12. |
|
Answer» |
|
| 3245. |
If (x-2) is a factor of 2x^(3)-x^(2)-px-2 (i) find the value of p. (ii) with the value of p, factorise the above expression completely. |
|
Answer» |
|
| 3246. |
Radius and height of a right circular cone and that of a right circular cylinder are respectively, equal. If the volume of the cylinder is 120cm^(3), then the volume of the cone is equal to ……… . |
|
Answer» `1200cm^(3)` |
|
| 3247. |
Prove that sqrt(7) is irrational. |
| Answer» | |
| 3248. |
Fin dthe remainder when 2^(24) is divided by 35. |
|
Answer» <P>2 |
|
| 3250. |
Two identical solid cones each of base radius 3 cm with vertical height 5 cm and one more solid cone of base radius 2 cm with vertical height 4.5 cm are jointly melted and recast into a solid sphere. Find : (i) the radius, (ii) curved surface area of the sphere. |
|
Answer» |
|