InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 14501. |
The minute hand of a big clock in 36 cms long how many cms does the extremity of the minute hand move in 20 minutes time. (use pi=22/7) |
| Answer» SOLUTION :`24pi`CMS | |
| 14502. |
Write the contrapositive and converse of the following statements. If the two lines are parallel, then they do not intersect in the same plane. |
|
Answer» If two LINES intersect in the same PLANE, then they are not PARALLEL The converse is If two lines do not interesect in the same plane, then they are parallel |
|
| 14503. |
sin x = 2/5, x lies in second quadrant. find trignometric ratio |
|
Answer» |
|
| 14504. |
Three coin are tossed once. Find the probability of getting (i) 3 heads, (ii) 2 heads, (iii) atleast 2 heads, (iv) atmost 2 heads, (v) no heads, (vi) 3 tails, (vii) exactly two tail, (viii) no tail, (ix) atmost two tails. |
|
Answer» |
|
| 14506. |
Sin^(-1)(4/5)-Sin^(-1)(5/13)= |
|
Answer» `SIN^(-1)(56/65)` |
|
| 14507. |
From a point on the level ground, the angle of elevation of the top of a pole is 30^@. On moving 20 metres nearer, the angle of elevation is 45^@. Then the height of the pole, in metres , is |
|
Answer» `10(sqrt(3)-1)` |
|
| 14508. |
[barbbarcbarbxxbarc]+{barb.barc}^(2)= |
|
Answer» `(BARB+BARC)^(2)` |
|
| 14509. |
i) Express (sin 4theta)/(sin theta) interms of cos^(3) theta and costheta ii) Express cos^(6)A+sin^(6)A interms of sin 2A iii) Express (1-costheta+sintheta)/(1+cos theta+sin theta) interms of tantheta/2 |
|
Answer» ii) `1-3/4 SIN^(2)2A` iii)`"TAN"theta/2` |
|
| 14510. |
Which of the following sets are finite or infinite : The set of odd natural numbers. |
|
Answer» |
|
| 14511. |
If the point (1, 2, 3) is changed to the point (2, 3, 1) through translation of axes, find the new origin. |
|
Answer» |
|
| 14512. |
If y = e^(x) sin ax and (d^(2)y/(dx^(2))-2dy/dx + 5y = 0 find a: |
|
Answer» 4 |
|
| 14514. |
If 2 sin ^(2) x + 3 sin x - 2 gt 0 and x^(2) - x - 2 lt 0 (x is measured in radians) then x lies in |
|
Answer» `((PI)/6, (5PI)/6)` |
|
| 14515. |
Point of intersection of the graph of sine function with X - axis has value zero. |
|
Answer» |
|
| 14516. |
A rod of length 12 cm moves with its ends always touching the coordinate axes. Determine the equation of the locus of a point P on the rod, which is 3 cm from the end in contact with the x-axis. |
|
Answer» |
|
| 14518. |
Evaluate : lim_(x to 0 ) ((1+6x^(2))/(1+4x^(2)))^(1/(x^(2))) |
|
Answer» |
|
| 14519. |
If x,y,inR satisfies (x+5) ^(2) + (y-12) ^(2) = (14)^(2), then the minimum vlaue ofsqrt (x ^(2) + y ^(2)) is "______" |
|
Answer» |
|
| 14520. |
Prove that C_(0)^(2)+C_(1)^(2)+C_(2)^(2)+….+C_(n)^(2)=(2n!)/((n!)^(2)). |
|
Answer» |
|
| 14521. |
If theta=pi/(2^n+1)then cos theta cos 2 theta cos 2^(2) theta...... Cos2^(n-1) theta is equal to |
|
Answer» `(1)/(2^(N))` |
|
| 14522. |
Prove that (1+cos""pi/10)(1+cos""(3pi)/10)(1+cos""(7pi)/10)(1+cos""(9pi)/10)=1/16 |
|
Answer» `1/8` |
|
| 14523. |
Find the middle term in the expansion of((x)/(3)+9y)^(10) |
|
Answer» |
|
| 14524. |
Find perpendicular distance from the origin to the line joining the points ( cos theta, sin theta) " and " ( cos phi , sin phi). |
|
Answer» |
|
| 14525. |
Find the equation of locus of point which lies on bisectors of angles between the co-ordinate axes. |
|
Answer» |
|
| 14526. |
If lim_(xto 1)(x^(2019)-1)/(x^(n)-1)=-(2019)/(2018) then n=…….. |
|
Answer» -2017 |
|
| 14527. |
x + y ge 4, 2x - y lt 0 |
|
Answer» CORRESPONDING equation : `x + y =4` It cuts the X-axis at A(4, 0) and Y-axis at B (0, 4). Join AB. At point (0, 0) from the inequation, 0`ge`4 (False) `:.`The solution of this inequation is that REGION of XY-plane divided by line AB in which (0, 0) does not lie. Second inequation : `2X - y lt 0 ` Corresponding equation : `2x - y = 0` This line passes through the pointsO(0, 0) and C(2, 4). Join OC by dotted line. At point (1, 0) , from the inequation, 2 lt 0 (False) `:.` The solution of this inequation is that region of XY-plane divided by line OC in which (1, 0) does not lie. 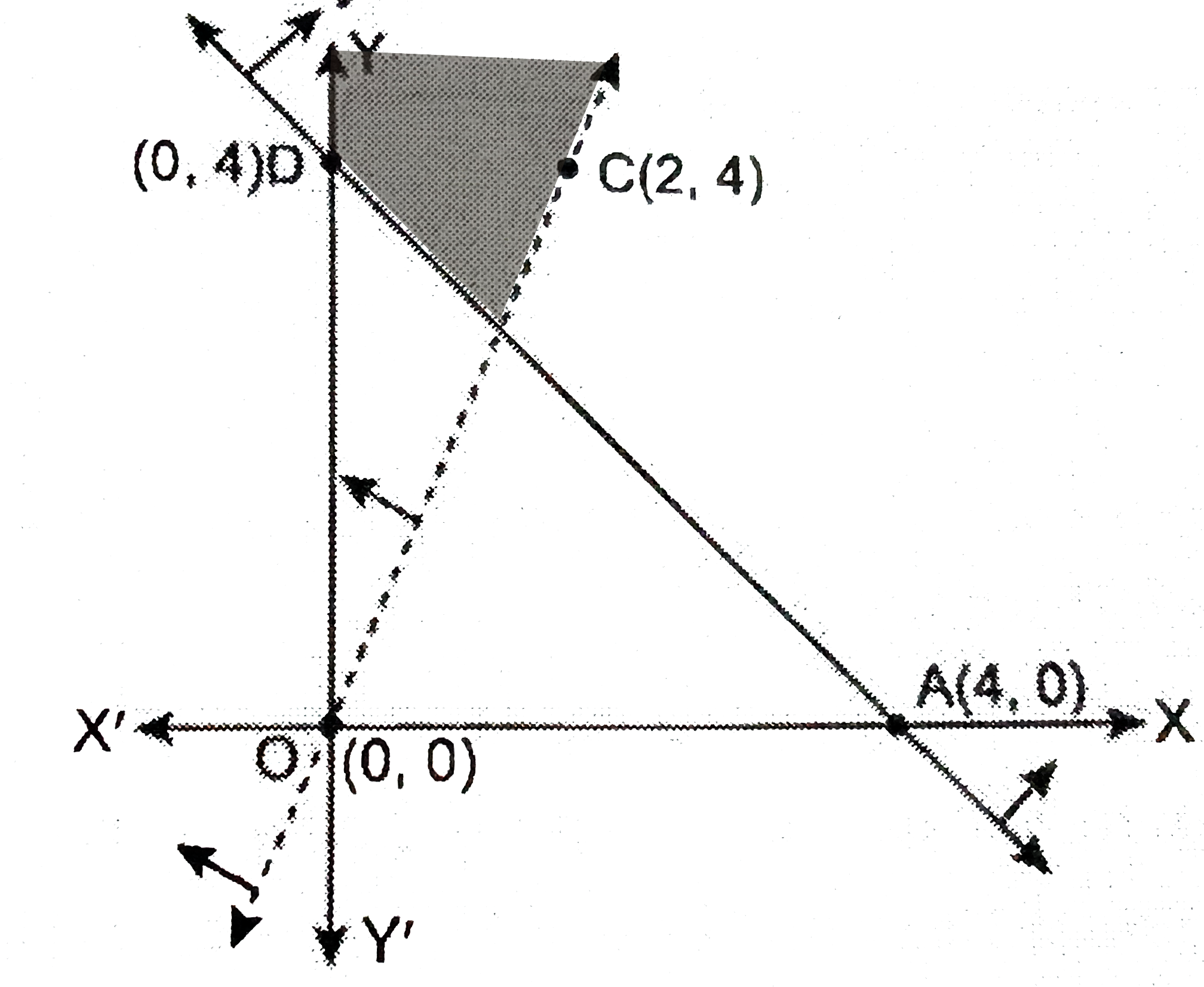 The common solution of two inequation is shown by the shaded part. |
|
| 14528. |
Length of latus rectum of ellipse 2x^(2)+81y^(2)=162 |
|
Answer» `(##KPK_AIO_MAT_XI_C11_E01_037_S02##)` |
|
| 14529. |
A line perpendicular to the line5x-y=0 form a triangle with the coordinate axes if the area of the triangle is 5 sq.units,then its equation is: |
|
Answer» `x+5ypm5sqrt(2)=0` |
|
| 14530. |
Find equation of the line which is equidistant from parallel lines 9x + 6y - 7 = 0 " and " 3x + 2y + 6 = 0 . |
|
Answer» |
|
| 14531. |
If the sides of trinangles arex^(2) + x+ 1,2 x + 1 , x^(-2) -1where,x>1,then the gratest angle is |
|
Answer» `pi//3` |
|
| 14532. |
If the vectors bara =bari - barj + 2bark, barb =2bari+4barj+bark and barc = gammabari - barj +mubark are mutually orthogonal, then (gamma,mu)= |
| Answer» ANSWER :D | |
| 14533. |
Which of the following is the nth term of an AP? |
|
Answer» `3-2n` |
|
| 14534. |
If 'theta' is an acute angle and the vector (sin theta)bari +(cos theta)bari " is perpendicular to the vector " bari -sqrt3barj, " then " theta = |
|
Answer» `pi/6` |
|
| 14535. |
Let f:(-1,1) rarr R be such that f(cos 4 theta) = (2)/(2-sec^(2) theta) for theta in (0, pi/4) uu (pi/4, pi/2). Then the value of f(1/3) is (are) |
|
Answer» `1- SQRT(3/2)` |
|
| 14536. |
Numbers of improper subsets of the given set A = {1,5,9} are 8 . |
|
Answer» |
|
| 14537. |
A =(1, 2, 3, 5) and B= {4, 6, 9). Define a relation R from A to B by R= {(x, y): the difference between x and y is odd, x in A, y in B}. Write R in roster form. |
|
Answer» |
|
| 14538. |
Find the equation of an ellipse whose latus rectum is 8 and eccentricity is 1/3 |
|
Answer» |
|
| 14539. |
If theta in (-(pi)/(4), (pi)/(4)) and x=log_(e ) [cot((pi)/(4)+theta)] Find Tanhx when theta=(pi)/(6) |
|
Answer» |
|
| 14540. |
Let U = { 1, 2, 3, 4, 5, 6, 7, 8, 9 }, A= { 1, 2, 3, 4}, B = { 2,4, 6, 8 } and C = { 3, 4, 5, 6 }. Find (A′)′ |
|
Answer» |
|
| 14541. |
Let U = { 1, 2, 3, 4, 5, 6, 7, 8, 9 }, A= { 1, 2, 3, 4}, B = { 2,4, 6, 8 } and C = { 3, 4, 5, 6 }. Find A' |
|
Answer» |
|
| 14542. |
Range of f(x)= (1)/(1- 2 cos x) is |
|
Answer» `[(1)/(3), 1]` |
|
| 14543. |
A line points (a,2a) and (-2,3) is perpendicular to the line 4x + 3y + 5 = 0 , find the value of a . |
|
Answer» |
|
| 14544. |
What is the coefficient of the (r+1)^(th) term in the expansion of (1+x)^n? |
| Answer» SOLUTION :`"^nC_r` | |
| 14545. |
Consider the line given by L_1=X+3Y-5=0, L_2=3x-ky-1=0 , match thestatements/expressions " in Column-I with the " statements /expression in Column-II. |
|
Answer» |
|
| 14546. |
If two tangents are drawn from a point to the circle x^(2)+y^(2)=32 to the circle x^(2)+y^(2)=16, then the angle between the tangents is : |
|
Answer» `(PI)/(4)` `S_(2):x^(2)+y^(2)=16` `rArr""S_(1)=0" is the director circle of "S_(2)=0` `rArr"Director circle is the LOCUS of two PERPENDICULAR tangents"` `"Angle is "(pi)/(2)` |
|
| 14548. |
Find the value of n such that (""^(n)P_(4))/(""^(n-1)P_(4))=(5)/(3), n gt 4 |
|
Answer» |
|
| 14550. |
Find the sixth term of the expansion of (y^(1//2) + x^(1//3) )^(n), if the binomial coefficient of the third term from the end is 45. |
|
Answer» |
|