InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 6301. |
If A = [{:(-qr , p(q + r) , pr + pq),(pq + qr, -pr, pq + qr ),(qr + pr, qr + pr, - pq):}] , then |A| equals |
|
Answer» <P>`(SUM pq)^(2)` |
|
| 6302. |
Proceedingfrom geometric reasoning, prove that : (a)if the function f(x)increases and has a concave graph in theinterval [a,b], then (b,a) f (a) lt int_(a)^(b) f(x) dx lt (b-a)""(f(a) + f(b))/(2) (b) if thefunction f(x) increases andhas a convexgraph in theinterval [a,b], then (b-a) ""(f(a) + f(b))/(2) lt int_(a)^(b) f(x) dx lt (b - a) f(b) |
|
Answer» `(B-a) f(a) LT int_(a)^(b) f(x) DX ` is OBVIOUS. |
|
| 6303. |
The zeros of the polynomial function g are 4 and -2. If the range of g is the set real numbers greater than or equal to -3, which of the following could be the graph of y=g(x) in the xy-plane? |
|
Answer»
|
|
| 6305. |
If |{:(alpha,x,x,x),(x,beta,x,x),(x,x,gamma,x),(x,x,x,delta):}| =f(x)-xf'(x) then f(x) is equal to |
|
Answer» `(x-alpha)(x-beta)(x-gamma)(x-delta)` |
|
| 6306. |
A trihedral prism with refracting angle 60^(@) deviates a light ray by 30^(@). The refractive index of the material of prism |
|
Answer» may be EQUAL to `sqrt(2)` `mu=("sin"((60+delta_(min))/(2)))/("sin"(60)/(2))le("sin"((60+30^(@))/(2)))/("sin"((60)/(2)))=sqrt(2)` `{:(,,mulesqrt(2),),(delta_(max)le30^(@),,,),(i+90-60ge30^(@),,rArrge0^(@),),(muge(2)/(sqrt(3)),,mu" sin "60^(@)GE1" sin "90^(@),):}` 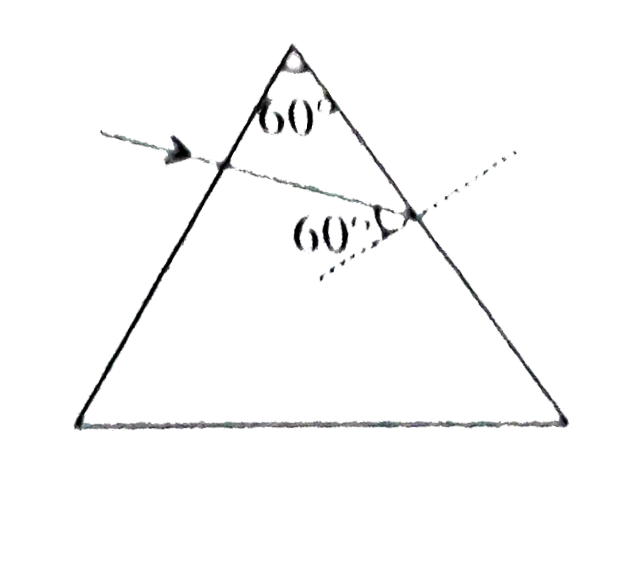
|
|
| 6307. |
Let f(x)=ax^(17)+bsinx.sin2x.sin3x+cx^(2) sgn(sin x)+d log (x+sqrt(1+x^(2)))+x(|x+1|-|x-1|)((e^(x)-e^(-x))/(e^(x)+e^(-x))) be defined on te set of real numbers, (agt0, b, c, d in R) if f(-7),f(-5)=-5, f(-2)=3, then the minimum number of zeroes of the equation f(x)=0 is equal to ________. |
|
Answer» So, `f(7)=-7, f(5)=f(2)=3` `XTO-oo,f(X)to oo` `xto oo, f(x) to oo` 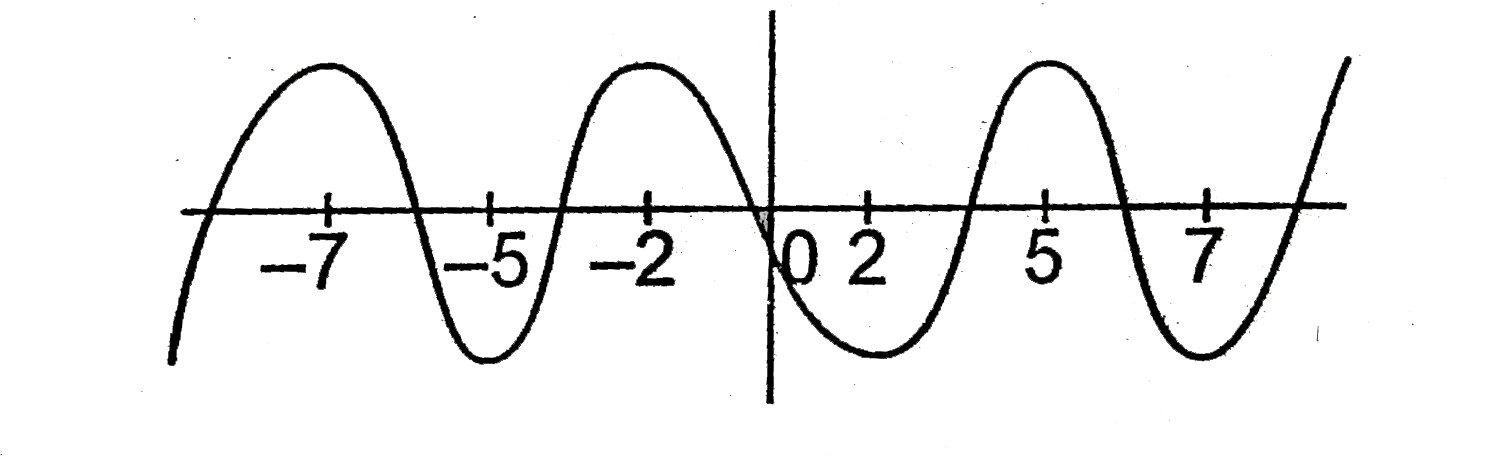
|
|
| 6308. |
If f : RR to R is an even function which is twice differentiable on RR and f ''(pi) =1., then f ''(-pi) = |
|
Answer» `-1` |
|
| 6309. |
Let p,q, r denote respectively the statements :" you are honest ", "you are laborious "," You will receive a promotion" Translate |r vv (~~p)| rarr ~~qstatements into English language. |
| Answer» SOLUTION :If you will RECEIVE a PROMOTION or you are not HONEST then you are not LABORIOUS. | |
| 6310. |
If lim_(x to 2) ((-ax+sin(x-2)+2a)/(x+sin (x-2)-2))^((2-x)/(sqrt2-sqrtx))=1/4^(sqrt2) then least 1+a^2 is |
|
Answer» |
|
| 6311. |
Determine whether a**b = "LCM" {a,b} "on" {0,1,2,3,4…..,10}operations as defined by * are binary operations on the sets specified in each case. Give reasons if it is not a binary operation. |
|
Answer» SOLUTION :LET A `={0,1,2,…….10}` `4,5 INA" but" 4**5 ="LCM"{4,5}` `=20 !in A` `:. **` is not a binary operation on A. |
|
| 6312. |
If P(bar(p))= 3i + j + 2k and Q(bar(q))=i-2j-4k the equation of plane passing through Q and perpendicular to line PQ is |
|
Answer» 2x+3y + 6z+16=0 |
|
| 6313. |
If thesumoftwoof therootsofx^4 -2x^3 -3x^2 +10 x-10=0is zerothentherootsare |
|
Answer» `+- SQRT(5) ,1 +-i` |
|
| 6314. |
The upper the portion of a vertical pole subcends an angle ta a point in the horizontal plane through its foot and advance 40 m from the foot. A possible height of the vertical pole is: |
| Answer» ANSWER :A | |
| 6315. |
Ifx = a( sin theta - theta cos theta)and y= a ( cos theta + theta sin theta) " find "(dy)/(dx) at theta = pi/4 |
|
Answer» |
|
| 6316. |
If 2x^(3) + 3x^(2) + 5x +6=0 has roots alpha, beta, gamma then find alpha + beta + gamma, alphabeta + betagamma + gammaalpha and alpha beta gamma |
|
Answer» |
|
| 6317. |
Prove theA uu B =B uu A results of the sections 1.13 and 1.14 that are stated with our proof. |
|
Answer» SOLUTION :LET `X in A UU B |
|
| 6318. |
A point ‘P ’ moves in xy plane in such a way that[|x|]+[|y|]=1, where [.] denotes the greatest function. Area of the region representing all possible positions of the point ‘P ’ is equal to : |
|
Answer» 4. sq. units |
|
| 6319. |
Iff(x)={{:(x^(2) " for " 0 le x le 1),(sqrt(x) " for "1 le x le 2):} then int_(0)^(2) f(x)dx= |
| Answer» Answer :B | |
| 6320. |
Integrate the function is. (1)/(sqrt(sin^(3)x sin(x+alpha))) |
|
Answer» |
|
| 6321. |
For a math homework assignment, Kerla found teh area and perimeter of a room of her house. She reported that the area of her rectangular living room is 180 square feet and that the perimeter is 54 feet. When drawing a sketch of her living room the next day, she realized that she had forgotten to write down the dimensions of the room. What are the dimensions of Karla's living room, in feet? |
|
Answer» 9 by 20 |
|
| 6322. |
sinx+siny=3/4 andsinx-siny=2/5 then (tan((x-y)/2))/(tan((x+y)/2))= |
|
Answer» `15/8` |
|
| 6323. |
Evaluate the following integrals. int(1)/(4sin^(2)x+3sinxcosx+2cos^(2)x)dx |
|
Answer» |
|
| 6324. |
How many six digited numbers that can be formed with 1, 2, 3, 4 if all the digits are to appear in the same number atleast once. |
|
Answer» |
|
| 6325. |
If bar(a)+bar(b)+bar(c)=bar(ab),bar(b)+bar(c)+bar(d)=betabar(a) and bar(a),bar(b),bar(c)are non-coplanar vectors then show that bar(a)+bar(b)+bar(c)+bar(d)=bar(0). |
|
Answer» |
|
| 6326. |
The value of (1+Delta)(1-Delta) is |
|
Answer» 0 `=(1+Delta){(1-grad)f(x)}` `=(1+Delta)[f(x)-{f(x)-f(x-h))]` `=(1+Delta)f(x-h)=Ef(x-h)` `[because (E=1+Delta)]` `=f(x)=1*f(x)` THUS, `(1+Delta ) (1-grad)f(x)=1*f(x),`for any function `f (x). `therefore (1+Delta)(1+grad)=1` |
|
| 6327. |
Let A=[{:(2, -1, 3), (4, 0, 2), (-3, 2, 6):}], find det (adj A). |
|
Answer» 2161 |
|
| 6328. |
{x in R: (14x)/(x+1)- (9x-30)/(x-4) lt 0} = |
| Answer» Answer :D | |
| 6329. |
Find the middle terms are are there in the expansion of (3a-5b)^6 ? |
|
Answer» |
|
| 6330. |
Consider the determinant Delta=|[0,2,6],[1,5,0],[3,7,1]|Write the co-factors of the elements in the first column. Hence, evaluate Delta |
|
Answer» SOLUTION :The co-factors are GIVEN below: `A_11=(-1)^(1+1)M_11=1xx5=5,` `A_21=(-1)^(2+1)M_21` `=-1xx-40=40` `A_31=(-1)^(3+1)M_31` `=1xx-30=30` `thereforeDelta=0xx5+1xx40+3xx-30` `=0+40-90=-50` |
|
| 6331. |
Find the other end of the diameter of the circle x^(2) +y^(2) -8x + 27 =0if one end of it is (2,3) |
|
Answer» |
|
| 6332. |
If the coefficient of rth termand (r+1)th term in the expansion of (1+x)^20 are in the ration 1:2, then r= |
|
Answer» 6 |
|
| 6333. |
Integrate the following functions (3x^2)/(x^6+1) |
|
Answer» Solution :LET t = `x^3`. Then `dt = `3x^2 DX` THEREFORE` int (3x^2)/(x^6+1) dx` =`int dt/(t^2+1) = tan^-1 t+C` =`tan^-1(x^3)+c` |
|
| 6334. |
A chord of negative slope from P(sqrt(264),0) is drawn to ellipse x^(2)+4y^(2)=16.This chord intersects the ellipse at A andB (O is the origin) |
|
Answer» the maximum AREA of `DeltaAOB` is 4 |
|
| 6335. |
Number of pointswhere f(X) = sqrt(x^(2)) +[x] ^(2) , x in [-2,2]isdiscontinuous is( where[.]re[presents thegreatestinterger function )______. |
|
Answer» |
|
| 6336. |
If a pair of dice is rolled until sum more than 10 appears first time. Find the probability of getting different numbers in last throw. |
|
Answer» |
|
| 6337. |
If a, b, c in Q and p + sqrt2 q ( p, q in Q) is an irrational root of ax^2 + bx + c = 0 then the other root is |
|
Answer» |
|
| 6338. |
Let omega be a imaginary root of x^(n)=1. Then (5- omega)(5- omega^2)"………"(5-omega^(n-1)) is |
|
Answer» `1` |
|
| 6339. |
If (2x^(2) - x - 1)^(5) = a_(0) + a_(1)x + a_(2)x^(2) + ....... + a_(10)x^(10) then, a_(2) + a_(4) + a_(6) + a_(8) + a_(10) = |
|
Answer» 15 |
|
| 6340. |
The transformed equation of x^(3) - 4x^(2) + (1)/(4)x - (1)/(9) = 0 , by eliminating fractional coefficients is |
|
Answer» `y^(3) + 15Y^(2)+ 52y - 36 = 0 ` |
|
| 6341. |
To each element of the set S = {1, 2, 3.....1000}, a colour is assigned. Suppose that for any two elements a, b of S, if 15 divides a + b they are both assigned the same colour. What is the maximum possible number of distinct colours used |
|
Answer» |
|
| 6342. |
When viewing an object near to your eyes the following are required for proper image formation of the retina ? (A) Contraction of the ciliary muscles (B) Increase in thickness of lens (C) Contriction of the pupil (D) Increased focal length of the lens |
|
Answer» A and C |
|
| 6344. |
Evalute the following integrals int (1)/(1 + (2x + 1)^(2)) dx |
|
Answer» |
|
| 6345. |
A regular polygon of n sides is constructed. No. of ways 3 vertices be selected so that no two vertices are consecutive is |
|
Answer» `""^(n)C_(3)-n.(n-4)` |
|
| 6347. |
If the coefficients of r^(th) , (r+ 1)^(th) and (r + 2)^(th) terms in the binomial expansion of (1 + y)^m are in A.P. then m and r satisfy the equation |
|
Answer» `m^2 - m (4R - 1) + 4r^2 + 2 = 0` |
|
| 6348. |
Find the position vector of a point R which divides the line joining the points P and Qwhose vectors i+2j-k and -i+j+k in the ratio 2:1 externally. |
|
Answer» SOLUTION :p.v.of R =`VEC(OR)` ` =(2(-overset^^i+overset^^j+overset^^k)-1(overset^^i+2overset^^j-overset^^k))/(2-1)` `-3overset^^i+3overset^^k` |
|
| 6349. |
(1)/(1+cotx) |
|
Answer» |
|
| 6350. |
The set of all values of the parameter 'a' for which the points of minimum of the function y=1+a^(2)x-x^(3)satisfy the inequality (x^(2)+x+2)/(x^(2)+5x+6)le0is |
|
Answer» An EMPTY SET ALSO `(x^(2)+x+2)/(x^(2)+5x+6)le0impliesx^(2)+5x+6lt0impliesx in (-3,-2)` If `a gt 0` than `x=-(a)/(sqrt(3))` is point of minima `implies - (a)/(sqrt(3)) in (-3,-2)implies a in (2sqrt(3),3sqrt(3))` If `a LT 0` then `x=(a)/(sqrt(3))` is point of minima `implies(a)/(sqrt(3))in (-3,-2)implies a in (-3sqrt(3),-2sqrt(3))` |
|