InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 6951. |
Let f(x) = 4x^(3) + 1. If the area of the region bounded by f(x) and x-axis from x = 0 to x = a is same as the area of region bounded by f(x) and x-axis from x = a to x = 3 then a lies in (a > 0) |
|
Answer» (0,1)  `int_(O)^(a) f(x) DX = int_(a)^(3) f(x) dx` `implies a^(4) + a = 84 - (a^(4) + a)` `a^(4) + a - 42 = 0` Let `g(a) = a^(4) + a - 42` `g(0) < 0, g(1) < 0, g(3) > 0` By IVT 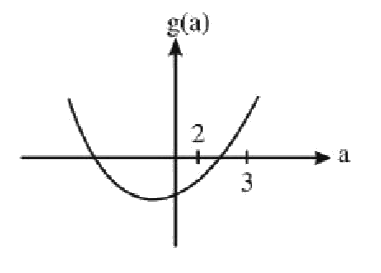 `a in (2, 3)`. |
|
| 6953. |
Number of ................ |
|
Answer» `t+16/t=10 implies t=2, 8` |
|
| 6954. |
If f:{x|xge1,"x" inR}rarr{x|xge2,x inR} f(x) =x+1/(x)then f^(-1)(x) = ......... |
|
Answer» `(X+SQRT(x^2-4))/2` |
|
| 6956. |
Construct a 2xx3 matrix having element:a_(ji)=i/j |
|
Answer» SOLUTION :`a_ji=i+ij` THEMATRIX is `[[1/1,1/2,1/3],[2/1,2/2,2/3]]=[[1,1/2,1/3],[2,1,2/3]]` |
|
| 6957. |
If 2veca, 3vecb,2(veca xx vecb) are position vectors of the vectors A,B,C, of triangleABC and |veca|=|vecb|=1,vec(OA).vec(OB)=-3 (where O is the origin), then |
|
Answer» TRIANGLE ABC is right-angled triangle `RARR 2.3costheta=-3` `rArr costheta=-1/2 rArr costheta=(2pi)/(3)` `=4|veca||vecb|^(2)sin^(2)theta+6veca.vecb=4.3/4-61/2=0` Angle C is `90^(@)`. |
|
| 6958. |
If a tangent to the curve y = 6x -''x^(2) is parallel to the line 4x - 2y - 1 =0, then the point of tangency on the curve is |
|
Answer» (2,8) |
|
| 6959. |
Fill int the blanks choosing correct answer from the bracket. If a cosB = b cosA, then cosB = _____. |
| Answer» ANSWER :C | |
| 6960. |
If truth-values of statements p andq are F and T respectively. Then the truth-value of |
|
Answer» `~PTO~q` is T |
|
| 6961. |
Evaluate the following integrals intsqrt(x)logxdx |
|
Answer» |
|
| 6962. |
sin 12^(@)sin 48^(@)sin 54^(@)= |
|
Answer» `1//2` |
|
| 6963. |
Find the domains of definaton of the following functions: (a) f(x)=sqrt(x-1)+sqrt(6-x) (b) f(x)=sqrt(x^2-x-2)+(1)/sqrt(3+2x-x^(2)) (c) f(x)=(x)/sqrt((x^(2)-x-2)) (d) f(x)=sqrt(sin x-1) (e) f(x)=sqrt(log""(5x-x^(2))/(4)), (f) f(x)=log_(x) 5, (g) f(x)=log ""(x^(2)-5x+6)/(x^2+4x+6) (h) f(x)=arc sin ""(x-3)/2-log(4-x) (i) f(x)=(1)/(log(1-x))+sqrt(x+2), (j) f(x)=log cos x, (k)f(x)=arc cos ""(3)/(4+2 sin x) (l) y=(1)/sqrt(|x|-x) |
|
Answer» |
|
| 6964. |
Using principle of mathematical induction, prove that 7^(4^(n)) -1 is divisible by 2^(2n+3) for any naturalnumber n. |
|
Answer» <P> Solution :Let `P(n) = 7^(4^(th)) - 1` be divisible by `2^(2n+3)``P(1) = 7^(4) - 1= (7^(2) - 1) (7^(2) + 1)` ` = 48 xx 50= 32 xx 75` `= 2^(5) xx 75`. whichis divisibleby `2^(2xx1+3)` Let usassume that the result is truefor n` = k`. i.e, `7^(4^(k)) - I` is divisible by `2^(2k+3)`but not by `2^(2k+4)`. `rArr 7^(4^(k)) - 1 = 2^(2k+3)`m , wherem issome oddnatural number Now, `7^(4^(k+1)) - 1 = (7^(4^(k)))^(4-1)` `= ((2^(2k+3)m+1)^(2) +1)((2^(2k+3)m+1)^(2)-1)` `= ((2^(2k+3)m+1)^(2) +1)(2^(2k+3)+2)(2^(2k+3)m)` `= (2^(4k+6)m^(2) + 2^(2k+4) m + 2)(2^(2k+3)m + 2) (2^(2k+3)m)` ltbr `= 2^(2k-5)(2^(4k+5)m^(2) + 2^(2k+3) m + 1)(2^(2^(2k+2)m +1) (m),` Which is divisivble by `2^(2k+5)` Thus, `P(k + 1)` is true whenever `P(k)`is true. So, by the PRINCIPLE of MATHEMATICAL induction, `P(n)` is true for any natural number n. |
|
| 6965. |
Differentiate sin x^(2) + sin^(2)x + sin^(2) (x^(2)) |
|
Answer» |
|
| 6966. |
If Rgergt0 and dgt0, then 0lt(d^(2)+R^(2)-r^(2))/(2dR)le1 |
|
Answer» is SATISFIED if `|d-R|ler` |
|
| 6967. |
The shortest distance between the lines 2x+y+z-1=0=3x+y+2z-2 and x=y=z, is |
|
Answer» `1/sqrt(2)` UNITS Line x=y=z is passing through the point O(0,0,). Required shortest distance = distance of O from the member plane of above family which is parallel to the line x=y=z If plane is parallel to the line, `(2x+3lambda)1+(1+lambda)1+(1+2lambda)1=0` `RARR lambda=-2/3` Equation of plane is `3(2x+y+z-1)-2(3x+y+2z-2)=0` or `y-z+1=0` Its distance from (0,0,0) is `1/sqrt(2)`. |
|
| 6968. |
y= sin x- cos x and f(x)= (d^(17)y)/(dx^(17)) " then " f((pi)/(4))= ……..[a]√2[b]1/√2[c](√2)^17[d]0 |
| Answer» Answer :A | |
| 6969. |
Using properties evaluate the following definite integrals, evaluate the following: int_0^1 x(1-x)^n dx |
|
Answer» SOLUTION :`int_0^1 X(1-x)^N DX` =`int_0^1 (1-x)(1-(1-x))^n dx` =`int_0^1 (1-x) x^n dx = int_0^1(x^n-x^(n+1))dx` =[x^(n+1)/(n+1) - x^(n+2)/(n+2)]_0^1` = 1/(n+1) -1/(n+2) = `((n+2)-(n+1))/((n+1)(n+2))` `1/((n+1)(n+2))` |
|
| 6970. |
Find the area of the circle4x^(2) + 4y^(2) = 9 which is interior of the parabola x^(2) = 4y. |
|
Answer» |
|
| 6971. |
Find the number of ways in which an examiner can assign 30 marks to 10 questions in a question paper. (fractional marks are not allowed) |
|
Answer» |
|
| 6972. |
Find the values of the following correct to five decimals.sqrt(3.96) |
|
Answer» |
|
| 6973. |
If the line ax +by+c = 0 where a, b, cinR and a, b,c notin 0 is a normal to the curve y=x^(2), then x^(3)+2a^(2)x+4a^(2)c = 0has |
|
Answer» three distinct real roots one of which is b |
|
| 6974. |
If a, b, c are distinct real numbers and P, Q, R are three points whose position vectors are respectively ahati + b hatj+ c hatk , b hati + c hatJ + a hatk and c hai + a hatj + b hatk, then angle QPR = |
|
Answer» `COS^(-1) (a +B+ c)` |
|
| 6975. |
Find the correct pair from the following(i)In a system of equations if Delta ne 0, Delta_(x)ne 0, Delta_(y)ne 0, Delta_(z)ne 0 then it has unique solution.(ii) Interchange of rows and columns is an elementary operation.(iii) (AB)^(-1)=B^(-1)A^(-1)(iv)(B)^(T)=A^(T)B^(T) |
|
Answer» (i) and (II) |
|
| 6976. |
Three persons A, B and C shot to hit a target. If A hits target 4 times in 5 trials B hits target 3 times in 4 trials C hits target 2 times in 3 trials Then find probabilities of following events. (i) All the person A, B and C hits the target. (ii) None of A, B and C can hits the target. (iii) At least 2 persons from A, B and C hits the target. |
|
Answer» |
|
| 6977. |
Two dice are thrown simultaneously. If X denotes the number of sixes, find the expectation of X. |
|
Answer» |
|
| 6978. |
Find the direction cosines of the line (x-2)/(2)=(2y-5)/(-3),z=-1. Also find the vector equation of the line. |
|
Answer» |
|
| 6979. |
By using the properties of definite integrals, evaluate the integrals int_(0)^(pi/2)2cos^(2)xdx |
| Answer» | |
| 6980. |
Kohl'soffersa special discountof 10 % onthe sellingpriceon all productsif paidin cash. However, at thesame time, the storecharges 20% extra( on thesellingprice)on all productsif paidusinga credit card . How muchdoes a customersaveon a SamsungTV listed at $3000 havinga discountof 20% as a promotionalofferformSamsungif hepaysin cashif he pays withacredit card ? |
|
Answer» 180 |
|
| 6981. |
Which of the following sentences are propositions and which are not ? Write with reason : x^2-x+1=0 |
| Answer» SOLUTION :`X^2-x+1=0` is not a STATEMENT as .x. is not DEFINED . | |
| 6982. |
If x_(n) + iy_(n) = (1 + i)^(n) then x_(n - 1) y_(n) - x_(n) y_(n- 1) = |
|
Answer» `2^(N-2)` |
|
| 6983. |
A certain sample of cuprous sulphide is found to have composition Cu_(1.8) S, because of presence of some Cu_(2+) ions in the lattice. What is the mole % of Cu_(2+) in crystal ? |
Answer» 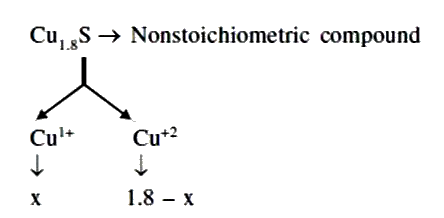 by law of conservation of charge `2 XX X + (1.8 -x) xx 1 = 2` `2x + 1.8 -x 2` `x = 2-1.8` `x = 0.2` `% Cu^(2+) = (0.2)/(1.8) xx 100= 11.11%`. |
|
| 6984. |
Which of the following curve is not symmetrical about both the axis? |
|
Answer»
|
|
| 6985. |
There are 10 points in a plane no three of which are collinear except 4 of them which lie on a line. The number of straight lines determined by them is |
|
Answer» 45 |
|
| 6986. |
Examine the continuity of the following functions at indicated points.f(x)={(sinfrac{1}{x}if xnea),(0 if x=0 atx=0):} |
|
Answer» Solution :f(0)=0 `lim_(xto0)sinfrac{1}{X}`does not exist.It oscillates between -1 and +1 As `lim_(xto0)f(x)=lim_(xto0)sinfrac{1}{x}` does not exist so the FUNCTION f(x) is DISCONTINUOUS at x=0 |
|
| 6987. |
A telegraphic wire suspended between two poles of height 15 mts is in the shape of a parabola. The distance between the poles is 20 mts and maximum sag of the cable wire is 4mt , then the height of the cable at a distance of 5 mt from one end is |
|
Answer» 12 |
|
| 6988. |
Assertion (A), The equation x^(2)+ 2|x|+3=0 has no real root.Reason (R): In a quadratic equation ax^(2)+bx+c=0, a,b,c in R discriminant is less than zero then the equation has no real root. |
|
Answer» Both A, R are true and R explain A |
|
| 6989. |
Find the eccentricity, length of a latus rectum, equations ofthe latus rectum of the hyperbola(x^(2))/(16)-(y^(2))/(9) =1. |
|
Answer» |
|
| 6990. |
The value of lim_(xto0^(+))(-1+sqrt((tanx-sinx)+sqrt((tanx-sinx)+sqrt((tanx-sinx)+…oo))))/(-1+sqrt(x^(3)+sqrt(x^(3)+sqrt(x^(3)+…oo)))) is |
|
Answer» `1/2` |
|
| 6991. |
A person goes 2 km east, then 3 km north, then 4km west and then 1 km north, starting from the origin. This point is taken as vector vec(A). The vector vec(B) such that 3vec(A)+5vec(B)=(9,32), is |
| Answer» ANSWER :D | |
| 6992. |
Find the number of distinct terms in the expansion of (x+(2)/(x)+1)^(20) |
|
Answer» |
|
| 6993. |
Correct statement about I and II |
|
Answer» I is REDUCING SUGAR |
|
| 6994. |
I : The number of solutions of the equation z^(2) + |z|^(2) = 0 is 2 II : The number of solutions of z^(2) + |z| = 0 is 3 Which of the statements are true |
|
Answer» only I |
|
| 6995. |
Ifxisnumericallysosmall sothatx ^ 2andhigherpowersofxcanbeneglected,then(1 +(2x )/(3)) ^(3//2). (32 +5x) ^(-1//5)isapproximatelyequalto |
|
Answer» ` (32 +31 x)/(64)` `=(1 + (2x ) /(3)) ^(3/2)(32 ) ^(-1/5) [ 1+(5x ) /( 32 ) ]^( -1//5 ) ` `=[ 1+(3 ) /(2)((2x ) /(3)) + …. ] ((1 )/(2)) [1- (5x ) /(32) ((1)/(5))+… ]` byneglecting `x^ 2`TERMS `= [1 + x ][ (1)/(2) ][ 1- (x )/(32)] ` `= (1)/(2)[ 1 -(x)/(32)+ x - (x ^ 2 )/(32) ] ` Byneglecting `x ^ 2`terms, we get, ` = (1)/(2) [ 1 +(31x)/(32)] ` `= (32 + 31 x ) /(64) ` |
|
| 6996. |
1 mole of a real gas changes it state from state-A(2bar, 3L, 100 K) to state -B (2bar, 5L, 200 K) at constant pressure and finally to state-C (3bar, 10 L, 300 K). If DeltaU_(BC) = 110 J and C_(Pm) ofgas =3R = 3 xx 8.3 JK^(-1)mol^(-1) then thoose the correct option(s) : |
|
Answer» `W_(AB) = 830 J` |
|
| 6998. |
Two intersecting circles have their radii 1 metre and sqrt(3) metre. The distance between their centres is 2 metre Then the overlapping area (in square metre ) is- |
|
Answer» `(19 PI + 6 sqrt(3))/(6)` |
|
| 6999. |
For f(x)=4x^(3)+3x^(2)-x-1, the range of vaues of (f(x_(1))-f(x_(2)))/(x_(1)-x_(2))is |
|
Answer» `(-oo,-(5)/(4))` |
|
| 7000. |
Two lines of regressions are represented by 4x + 10y = 9 and 6x + 3y = 4. Find the line of regression y on x. |
|
Answer» |
|