InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 7051. |
f(x) = underset(1)overse(sinxcosy)/(y^(2)+y+1)dy, then |
|
Answer» `f'(X) = 0 AA x = (NPI)/(2), N in Z` |
|
| 7052. |
Integration of some particular functions : int(tanx)/(4+9 tan^(2)x)dx=....x+c |
|
Answer» `(2)/(3)tan^(-1)((2)/(3)tanx)` |
|
| 7054. |
Refers to question 12.i.eZ represents cost , if Z=400x+200y, x+2y ≥ 30, x-y=0 and 5x+2y ≥ 30,What will be the minimum cost? |
|
Answer» On solving y ≥ x and 5x+2y=30, we GET `y(30)/(7),x=(30)/(7)` 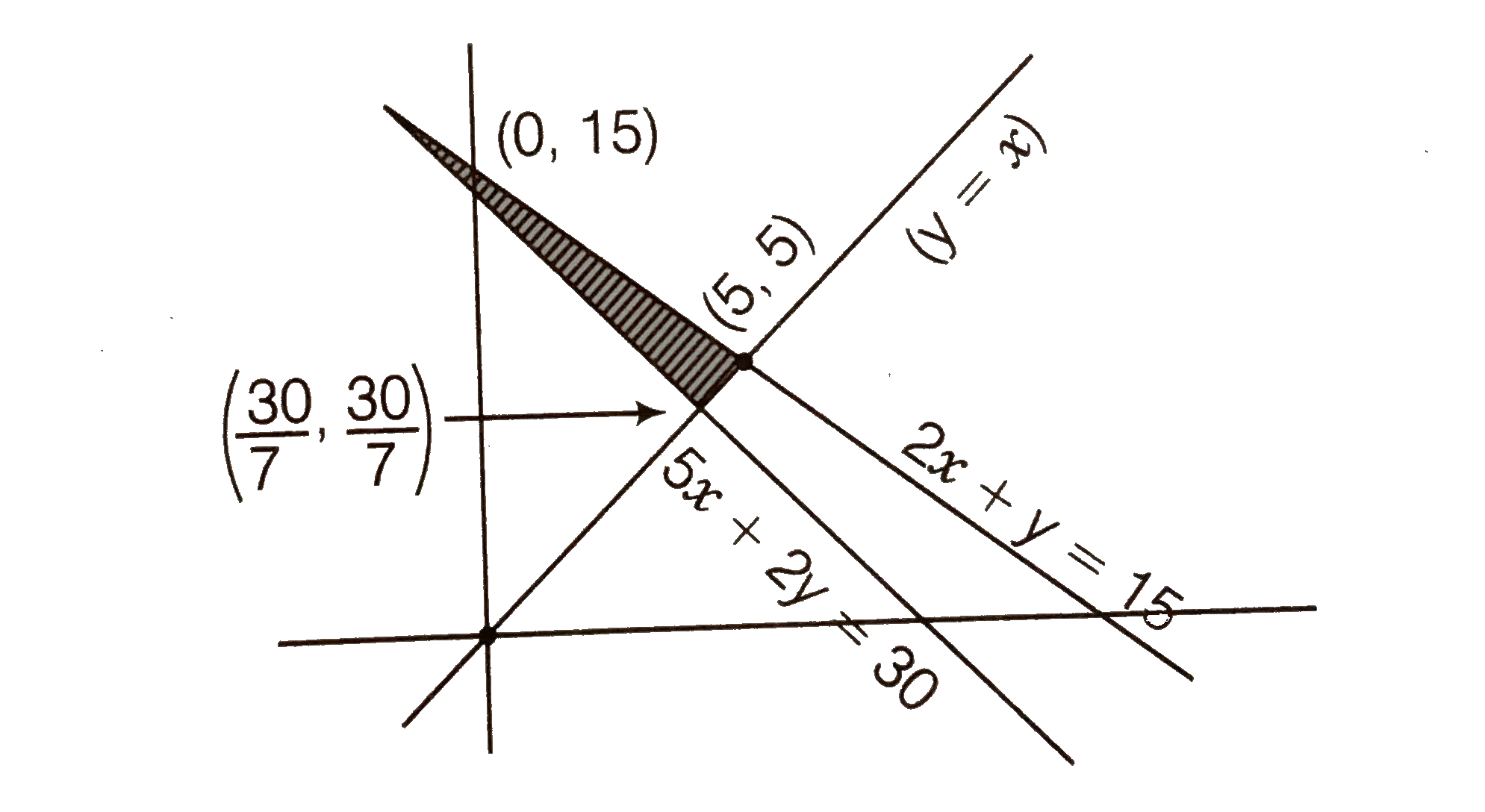 On solving x-y=0 and 2x+y=15, we get x=5, y=5 So, from the shaded FEASIBLE region it is clear that CORRDINATES of corner points are (0,15), (5,5) and `((30)/(7),(30)/(7))`  HENCE the minimum cost is 2571.43 |
|
| 7055. |
Discuss the continuity of the function f defined by f(x)= (1)/(x), x ne 0 |
|
Answer» |
|
| 7056. |
If x: y : = tan ((pi)/15 + alpha): tan ((pi)/15 + beta): tan ((pi)/15+ gamma)," then "(z+x)/(z-x) sin^(2) (gamma - alpha ) + (x+y)/(x-y) sin^(2) (alpha - beta ) + (y + x) / (y-z) sin^(2) (beta-gamma)= |
|
Answer» `SIN^(2)THETA` |
|
| 7057. |
Draw the graph of the following function. f((x)/(2)) |
|
Answer» `(##ARH_AMA_DIF_CAL_C04_E02_009_A01##)` |
|
| 7058. |
A 12 metre tall tree was broken into Two it was found that the height of the part which was left standing was the cube root of the length of the part that was cut away. Formulate this into a mathematical problem to find the height of the part which was cut away. |
|
Answer» |
|
| 7059. |
Find derivatives of the following functions.sqrt(tan(3z)) |
|
Answer» SOLUTION :`y = sqrt(tan3z) dy/dz = 1/(2sqrt tan3z). d/dx(TAN 3z) [because d/dz(sqrt U) = 1/(2sqrt u) (du)/dx =1/(2sqrttan 3z).sec^2(3z).d/dz(3z) = (3sec^23z)/(2sqrt tan 3z)` |
|
| 7060. |
If a term independent of x is to exist in the expansion of (x + (1)/(x^2))^n then n must be |
|
Answer» a MULTIPLE of 2 |
|
| 7061. |
Determine the differentials in each of the following cases. y = x^3 - 1 |
|
Answer» SOLUTION :`y = x^3 - 1` Then DY = `3x^2` DX |
|
| 7062. |
Show that i) baraxx(baraxx(baraxxbarb))=(bara.bara)(barbxxbara) ii) {(baraxxbarb)xx(baraxxbarc)}.bard=(bara.bard)[bara barb barc] |
|
Answer» |
|
| 7064. |
A fruit grower can use two typesof fertilizer in his garden, brand P and brand Q. The amounts (in kg) of nitrogen, phosphoric acid, potash, and chlorine in a bag of each brand are given inthe table. Tests indicate that the garden needs at least 240 kg ofphosphoric acid, at least 270 kg of potash and at most 310 kg of chlorine. If the grower wants to minimise the amount of nitrogen added to the garden, how many bags of each brand be used ? What is the minimum amount of nitrogen added in the garden ? |
|
Answer» |
|
| 7065. |
If 4 out of 12 scooter driver persons do not carry driving licence what is the probability that a traffic inspector who randomly selected 4 scooter driver person will catch at least 2 for not carrying driving licence. |
|
Answer» |
|
| 7066. |
What fruit or vegetable generated the third highest sales in April for Produce Stand P? |
|
Answer» tomatoes |
|
| 7067. |
Theregionshaded vertically is represented by the inequation |
|
Answer» `XGE0,x+2yle8,3x+2yge12` |
|
| 7068. |
Lori deposists $100 in a savings account at 2% interest, compounded annually. After three years, what is the balance on the account? (Assume Lori makes no withdrawals or deposits.) |
|
Answer» |
|
| 7069. |
If the projection of the vector a on b is |axxb| and if 3b=hati+hatj+hatk, then the angle between a and b is |
|
Answer» `(pi)/(3)` `rArr (a.b)/(|b|)=|axxb|` `rArr (|a||b|costheta)/(|b|)=|a||b|sintheta` `rArr tan theta=(1)/(|b|)` `rArr tan theta= (1)/((1)/(3)sqrt(1^2+1^2+1^2))` `rArr tan theta = sqrt(3)` `rArr theta=(pi)/(3)` . |
|
| 7070. |
Find the shortest distance between the lines l_1 and l_2 whose vector equations arevecr=hati+hatj+lambda(2hati-hatj+hatk) and vecr=2hati+hatj-hatk+mu(3hati-5hatj+2hatk). |
|
Answer» |
|
| 7071. |
{{:((|x|)/(x)","if x ne 0 ),(0"," if x = 0 ):} |
|
Answer» Solution :`{{:((|x|)/(x)","if x NE 0 ),(0"," if x = 0 ):}` at x = 0 f(0) =0 R.H.L = ` underset (x to 0^(+))(LIM)f(x)` LET 0 + h = x `rArr0 + h to x ` `rArrh to 0 ` ` underset (h to 0)(lim)(0+h)= underset (h to 0)(lim)(|h|)/(h) ` ` underset (h to 0)(lim)(h)/(h) underset (h to 0)(lim)(1)= 1 ` `:'` f(0) `ne` R.H.L. `:.` f(x) is discontinuous at x = 0 |
|
| 7072. |
Evaluate the following inegrals int(secxcosecx)/(log(tanx))dx |
|
Answer» |
|
| 7073. |
If theline y=x touches the circle x^(2)+y^(2)+2gx+2fy+c=0 at P where OP=6sqrt2 then c= |
|
Answer» 36 |
|
| 7074. |
Prove that if the figure S is bounded by a simple convex contour and is situated between the ordinates y_(1) and y_(2), then the volume of the solid generated by revolving this figure about the x-axis can be expressed by the formula V= 2pi int_(y_(1))^(y_(2)) yh dy, where h= x_(2) (y) - x_(1) (y), x= x_(1) (y) being the equation of the left portion of the contour and x= x_(2) (y) that of the right portion. |
|
Answer» |
|
| 7075. |
Let ** be a binary operation on the set Q of rational numbers as follows : a "*" b = a+ab Find which of the binary operations are commutative and which are associative. |
|
Answer» |
|
| 7077. |
If f(x)=xtan^(-1)x, then lim_(xto1)(f(x)-f(1))/(x-1)= |
|
Answer» `(pi+3)/(4)` |
|
| 7078. |
IF""^(n) C_(r-1):""^(n )C_(r) := 2: 4 :then(n,r)= |
|
Answer» `(10,4)` |
|
| 7079. |
At present, a firm is manufacturing 2000 items. It is estimated that the rate of change of production P w.r.t additional number of workers x is given by (dp)/(dx)=100-12sqrt(x). If the firm employss 25 more workers. Then the new level of production of items is |
|
Answer» 2500 |
|
| 7080. |
If f (x)= {{:(sin ^(-1) (sin x) , x gt 0),( (pi)/(2), x = 0), (cos ^(-1) (cos x) , x lt 0):}, then |
|
Answer» `X =0` is a point of maxima |
|
| 7081. |
Evaluate the following integralsint_0^1x^(1/3)dx |
| Answer» SOLUTION :`int_0^1x^(1/3)DX=[X^(4/3)/(4/3)]_0^1=3/4` | |
| 7082. |
Mr. B has two fair 6-sided dice, one whose faces are numbered1 to 6 and the second whose faces are numbered3 to 8. Twice, he randomly picks one of dice (each dice equally likely) and rolls it. Given the sum of the resulting two tolls is 9. The probabilityhe rolled same dice twice is (m)/(n)where m and n are relatively prime positiveintegers. Find (m+n). |
|
Answer» |
|
| 7083. |
Compute the area enclosed by the cardioid: x= a cos t(1 + cos t), y= a sin t(1 + cos t) |
|
Answer» |
|
| 7084. |
Find the unit vector parallel to the sum of the vectors veca = 2hati+4hatj-5hatk and vecb = hati+2hatj+3hatk. Also find its direction cosines. |
|
Answer» Solution :`veca+vecb = 2hati+4hatj-5hatk+hati+2hatj+3hatk` = `3hati+6hatj-2hatk` `|veca+vecb| = SQRT(9+36+4) = 7` UNIT VECTORS PARALLEL to `veca+vecb = (3hati+6hatj-2hatk)/7` D cs. are 3/7, 6/7, -2/7. |
|
| 7085. |
If int(1)/(x^(2)-2 sin alpha+1)dx=sec alpha.tan^(-1)(mx+c), then |
|
Answer» `m=sec ALPHA, C in R` |
|
| 7086. |
A relation R on the set of non-zero complex number is defined by Z_(1) R Z_(2) ltimplies (Z_(1)-Z_(2))/(Z_(1) + Z_(2)) is real then |
|
Answer» R is symmetric but not transitive `(Z-Z)/(Z+Z) =0 =` a real number `rArr` R is symmetric If `(Z_(1)-Z_(2))/(Z_(1) + Z_(2))` and `(Z_(2)-Z_(3))/(Z_(2) + Z_(3))` are real, then `(Z_(1)-Z_(3))/(Z_(1) + Z_(3))` is ALSO a real number. `rArr R` is transitive. |
|
| 7087. |
If a circle is concentric with the ellipse, find the inclination of their common tangent to the major axis of the ellipse. |
|
Answer» |
|
| 7088. |
A bridge is in the shape of a semi ellipse . If it is 400 m long and has a maximum height of 10 m at midpoint . The height of the bridge distanced 80m fromone end is |
| Answer» ANSWER :B | |
| 7089. |
I. Sin^(-1)x=x has only one solution II. Cos^(-1)x=x has only one solution |
|
Answer» only I is true |
|
| 7090. |
Show that the angle between the lines given by (a+2hm+bm^2)x^2+2 {(b-a)m-(m^2-1)h} xy+(am^2-2hm+b)y^2=0 is the same whatever be thevalue of m ,. |
|
Answer» |
|
| 7091. |
If the point z=(1+i)(1+2i)(1+3i)…..(1+10 i) lies on a circle |
|
Answer» `10!` |
|
| 7092. |
inte^x/x(1+xInx)dx |
|
Answer» Solution :`inte^x/x(1+xInx)DX` =`inte^xdx+inte^xInxdx` [INTEGRATING by parts TAKING `e^x` as FIRST and 1/x as second function.] =`e^x.Inx-inte^x.Inxdx+inte^xInxdx+C` =`e^x.Inx+C` |
|
| 7093. |
int(cosx)/(sqrt(3sin^(2)x-4sinx+5))dx |
|
Answer» |
|
| 7094. |
Which of the following is the best approximation to ((2^(3)-1) (3^(3)-1)……..(1000^(3)-1))/((2^(3)+1)(3^(3)+1)…..(1000^(3) +1)) |
|
Answer» |
|
| 7095. |
[1" "x" "1][{:(1,3,2),(0,5,1),(0,3,2):}][{:(1),(1),(x):}]=0then x=………… |
|
Answer» 1 |
|
| 7096. |
If I_(1)= int_(0)^(3pi) f( sin^(2) x)dx and I_(2)= int_(0)^(pi) f(sin^(2)x)dx then |
|
Answer» `I_(1)=I_(2)` |
|
| 7097. |
Log (log i) = |
|
Answer» `LOG [ ((PI)/(2)) + i((pi)/(2))]` |
|
| 7099. |
Differentiate sin sqrtx + cos^(2) sqrtx |
|
Answer» |
|
| 7100. |
Select incorrect statement for plasma :- |
|
Answer» Straw COLOUR viscous fluid |
|