InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 7951. |
Coefficient of constant term in the expansion of (x^(3)+5(3)^(-logsqrt3sqrt(x^(3))))^(4) is |
| Answer» Answer :D | |
| 7952. |
A problem of mathematics is given to three students and probability of solving the problem is(1)/(3), (1)/(3), (1)/(3) respectively. The probability that at least one of them solves the problem is ………… |
|
Answer» `(1)/(27)` |
|
| 7953. |
{:("Column A" , "Jack, Karl,Marc. and Kate are","ColumnB"),(, "friends . They collected just",),(, "enough money to buy a car.Jack",),(,"contributed 1/3 of what his three",),(,"friends contributed together.Karl",),(,"friends contributed together.Marc",),(,"contributed 2/5 of what his three ",),(,"friend contributed together",),("The amount paid by Jack", ,"The amount paid by Marc"):} |
|
Answer» If column A is LARGER |
|
| 7954. |
Show that the line passing through the points (4, 7, 8) and (2, 3, 4) is parallel to the line passing through the points (-1, -2, 1) and (1, 2, 5). |
|
Answer» |
|
| 7955. |
Find derivatives of the following functions.sec (tantheta) |
|
Answer» SOLUTION :`y = SEC (TAN THETA) DY/(d theta){sec(tan theta)} sec(tan theta). tan(tan theta).d/(d theta)(tan theta) = sec(tan theta). tan(tan theta). sec^2theta` |
|
| 7956. |
Two medians drawn from acute angles of a right angled triangles intersect at an angle pi//6. If the length of the hypotenuse of the triangle is 3 units, then area of the traingle (in sq. units) is |
|
Answer» Solution :`because ""AC=3impliesa^(2)+b^(2)=9` SLOPE of `AD=(-2b)/(a)` Slope of `CF=(-b)/(2a)` `therefore""tan.(pi)/(6)=|(-(2b)/(a)+(b)/(2a))/(1+(b^(2))/(a^(2)))|=|(-3ab)/(2(a^(2)+b^(2)))|=(3ab)/(9xx2)=(1)/sqrt(3)=(ab)/(6)impliesab=2sqrt(3)` `DeltaABC = (1)/(2)ab=sqrt(3)` 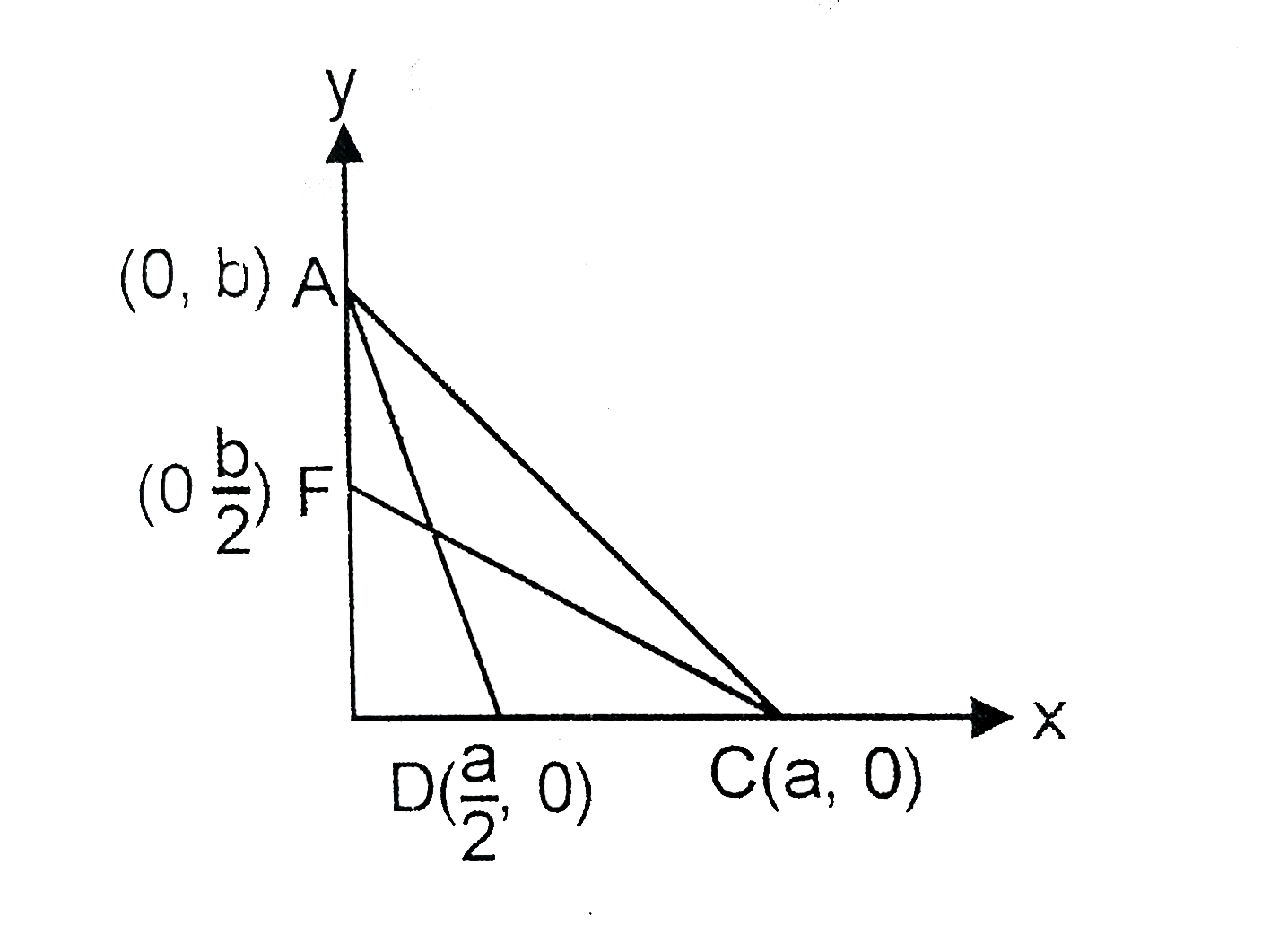
|
|
| 7957. |
If (3pi)/(2) lexle2pi " then :"sin^(-1) (sinx)= ... |
| Answer» Answer :A | |
| 7958. |
Let K = 1 ^(@), then 2 sin 2K + 6 sin 6K + ….+ 180 sin 180 k isequal to |
|
Answer» 90 cos K |
|
| 7959. |
A unit vectorvec amakes angles pi/4\ a n d\ pi/3withhat i\ a n d\hat jrespectively and an acute angle thetawithhat kdotFind the angle thetaand components ofvec adot |
|
Answer» |
|
| 7960. |
If mean deviation through median is 15 and median is 450, then coefficient of mean deviation is |
|
Answer» `1//30` |
|
| 7961. |
Areaboundedby thecurvey=x^3the x-axisand theordinatesx=-2andx=1is |
|
Answer» `-9` |
|
| 7962. |
Using integration, find the area of the region bounded by the lines y=1+abs(x+1), x=-2, x=3 and y=0. |
|
Answer» |
|
| 7963. |
If vecA=3hati+4hatj, vecB=6hati+8hatj and vecC=15/sqrt2(hati-hatk) then a vector (vecP) having magnitude equal to the magnitude of vecA+vecB in the direction of sqrt2 vecC is : |
|
Answer» `vecP=vecA+vecB` |
|
| 7964. |
If |z + barz| + |z - barz| = 2 then z lies on |
|
Answer» a straight line |
|
| 7965. |
{:("Column A","", "Column B"),("The perimeter of the triangle",,"The The circumference of the circle"):} |
|
Answer» If COLUMN A is larger |
|
| 7966. |
If there is an error of pm0.04 cm in the measurement of the diameter of a sphere, then the approximate percentage error in its volume, when the radius is 10 cm, is |
|
Answer» `pm1.2` |
|
| 7967. |
cos(x-y)=3cos(x+y) then cotxcoty= |
|
Answer» 1 |
|
| 7968. |
A square is inscribed in the circle x^(2)+y^(2)+2x+4y3=0. Its sides are parallel to the coordinates axes, then find the vertices of a square. |
|
Answer» |
|
| 7969. |
If vec(a)=3hati-hatj+2hatk,vec(b)=hati-3hatk and vec( c )=hati+2hatj then find (i) vec(a).vec(b)(ii) (vec(a)+vec(b)).vec( c ) (iii) (vec(a)-vec(b)).(vec(b)-vec( c )) (iv) (vec(a)+2vec(b)).vec(b) (v) (vec(a)-3vec( c )).(2vec(a)+vec(b)) |
|
Answer» |
|
| 7970. |
The p.m.f. of a r.v. X is as follows : P(X=0)=3k^(3),P(X=1)=4k-10k^(2),P(X=2)=5k-1, P(X=x)=0" for any other values of x, then c.d.f. F (X)" is |
|
Answer»
|
|
| 7971. |
Find the maximum area of an isosceles triangle inscribed in the ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2))=1 with its vertex at one end of the major axis. |
|
Answer» |
|
| 7972. |
In triangleABC the mid points of the sides AB,BC and CA are respectively (l,0,0),(0,m,0) and (0,0,n) . Then (AB^(2)+BC^(2)+CA^(2))/(l^(2) +m^(2)+n^(2))is equal to |
|
Answer» 2 |
|
| 7973. |
By giving a counter example, show that the following statement 'if n is an odd integer, then n is prime' is false. |
|
Answer» |
|
| 7974. |
If Arg ((z+1)/(z-1))=pi/6then the locus of z = x + iy is |
|
Answer» `x^(2) + y^(2) + 3x - 2 = 0 , y = 0` |
|
| 7975. |
An investigator interviewed 100 students to determine their preferences for the three drinks : milk (M) , coffee (C ) and tea (T) . He reported the following : 10 students had all the three drinks M, C, T , 20 had M and C only , 30 had C and T , 25 had M and T , 12 had M only , 5 had C only , 8 had T only . Find how many did not take any of the three drinks |
|
Answer» 10 |
|
| 7976. |
The mean and standard deviation of a distribution of weights of a group of 20 boys are 40 kg and 5 kg respectively. If two boys of weights 43 kg and 37 kg are excluded from this group, then the variance of the distribution of weights of the remaining group of boys is |
|
Answer» 26.18 |
|
| 7977. |
Show that the lines y=0, sqrt(3y)-xy=sqrt(3) and sqrt(3y)+x-10=0 form a cyclic trapezium. Determine the centre and the radius of the circle and also the area of the trapezium. |
|
Answer» |
|
| 7978. |
Consider a parabola P touches coordinate axes at (4,0) and (0,3). if focus of parabola P is (a,b) then the value of b-a is |
|
Answer» `1/25` |
|
| 7979. |
Evaluate the definite integrals int_(0)^((pi)/(4))(sinx+cosx)/(9+16sin2x)dx |
|
Answer» |
|
| 7980. |
For all integers, n ge 1 which of the following is divisible by 9. |
|
Answer» `8^(n)+1` |
|
| 7981. |
Length of chord of parabola y^(2) =4axwhose equation is y-sqrt2 x + 4 sqrt2 a =0 |
|
Answer» ` 2sqrt(11A) ` |
|
| 7982. |
Evalute the following integrals int sqrt(x)log xdx |
|
Answer» |
|
| 7983. |
If 0lt0ltpi/2" and "|{:(1+sin^(2)theta,cos^(2)theta,4sin4theta),(sin^(2)theta,1+cos^(2)theta,4sintheta),(sin^(2)theta,cos^(2)theta,1+4sintheta):}|=,"then "theta= |
|
Answer» `pi/24,(5PI)/(24)` |
|
| 7984. |
A matrix A has x rowsand x+5 column . A matrix B has y rows and 11 -y column . A matrix B has y rows and 11 - y column . If AB and BA are exist then the value of x and y are respectively ……….. |
|
Answer» 3,9 |
|
| 7985. |
Compute the area of the a surface generated by revolving about the x-axis an are of the curve x= t^(2) , y= (t)/(3) (t^(2)-3) between the points of intersection of the curve and the x-axis |
|
Answer» |
|
| 7986. |
show that the function is always differentiable . |
| Answer» | |
| 7987. |
Write bond-line structural formulas for (a) two primary (b) CH_(3)CHCH_(2)CH_(3)alcohols,a secondary alcohol, and (e) a tertiary alcohol - all having the molecular formula C_(4)H_(10)O |
|
Answer» Solution :`CH_(3)CH_(2)CH_(2)CH_(2)OH` and `CH_(3)underset(CH_(3))underset(|)(CHCH_(2)OH)` (B) `CH_(3)underset(OH)underset(|)(CH)CH_(2)CH_(3)` (c ) `CH_(3) - underset(CH_(3))underset(|)overset(CH_(3))overset(|)C-OH` |
|
| 7988. |
Iiv) If (2x^(3)+1)/((x-1)(x+1)(x+2))=A+(B)/(x-1)+(C)/(x+1)+(D)/(x+2), then find the value of A+B+C+D. |
|
Answer» |
|
| 7989. |
Problem of mathematics is given to three students and their respective probability of solving the problem is (1)/(3),(1)/(3) and (1)/(3). Find probability of an event that exactly one student can solve problem. |
|
Answer» |
|
| 7990. |
Draw the graph of y=cos^(-1)((1+x^(2))/(1+x^(2))) |
|
Answer» Solution :We have `y=F(x)=cos^(2)((1+x^(2))/(1+x^(2)))` LET `x=tantheta, theta in (-pi//2, pi//2)` `rArr""theta=tan^(-1)x` Now `cos^(-1)((1-x^(2))/(1+x^(2)))=cos^(-1)((1-tan^(2)theta)/(1+tan^(2)theta))` `=cos^(-1)(cos2theta)` `=cos^(-1)(cos2theta)," where "alpha in (-pi, pi)` Now consider the graph of `y=cos^(-1)(cos alpha)," where "alpha in (-pi, pi)`  From the graph. `cos^(-1)((1-x^(2))/(1+x^(2)))=cos^(-1)(cosalpha)` `={{:(-alpha,-piltalphalt0),(alpha,0lealphaltpi):}` `={{:(-2tan^(-1)x,-pilt2tan^(-1)xlt0),(2tan^(-1)x, 0le2tan^(-1)xltpi):}` `={{:(-2tan^(-1)x,-pilt2tan^(-1)xlt0),(2tan^(-1)x, 0le2tan^(-1)xltpi//2):}` `={{:(-2tan^(-1)x,xlt0),(2tan^(-1)x,xge0):}` `f'(x)={{:(-2/(1+x^(2)),xlt0),(2/(1+x^(2)),XGT0):}` So f(x) is non-differentiable at x = 0 `UNDERSET(xtooo)(lim)(-2tan^(-1)x)=pi,f(0)=2tan^(-1)(0)=0` Thus, `cos^(-1)((1-x^(2))/(1+x^(2)))" decreases form "pi" to "0" as increases from"-oo" to 0".` `underset(xtooo)(lim)(2tan^(-1)x)=pi` Thus, `cos^(-1)((1-x^(2))/(1+x^(2)))" increases form 0 to "pi" as x increses from 0 to"oo`. From this INFORMATION, we can draw the graph of `y=cos^(-1)((1-x^(2))/(1+x^(2)))` as shown in the following figure. 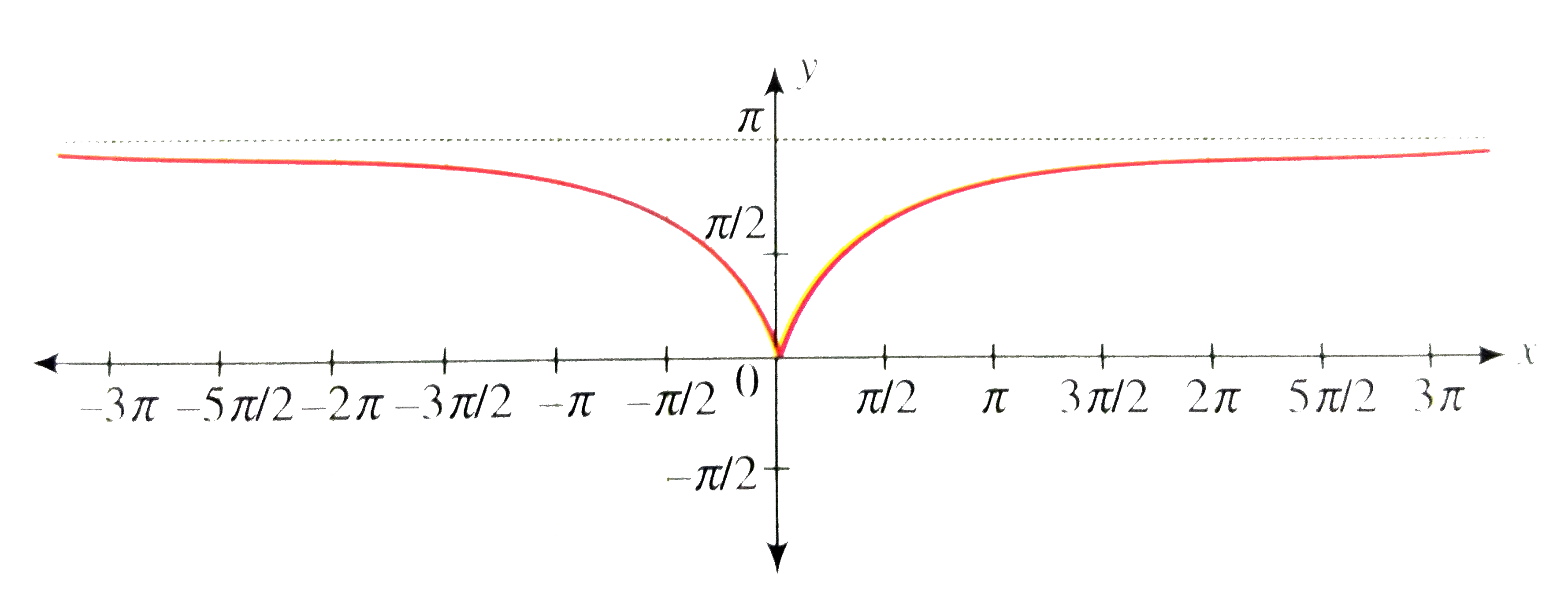
|
|
| 7991. |
Differentiate the functions with respect to x in Exerecises 1 to 8. 2sqrt(cot(x^2)) |
|
Answer» |
|
| 7992. |
Four tickets marked 00, 01, 10 , 11 respectively are placed in a bag. A ticket is drawn at random five times being replaced each time. The probability that the sum of the numbers on the tickets is 22 is |
|
Answer» `(2)/(7)` |
|
| 7993. |
Identify the planes containing the points ! (7,0,4),(2,-5,0),(0,sqrt2, -3) |
| Answer» SOLUTION :xz-plane, xy-plane, yz-plane. | |
| 7994. |
Choose the correct answer int(dx)/(sin^(2)xcos^(2)x) equals |
|
Answer» TAN X + COT x + C |
|
| 7995. |
Where I denotes set of integers, then n(A cap B)= |
|
Answer» 45 |
|
| 7996. |
If alpha, beta & gamma real numbers, then value of |(1,cos(beta-alpha),cos(gamma-alpha)),(cos(alpha-beta),1,cos(gamma-beta)),(cos(alpha-gamma),cos(beta-gamma),1)| is equal to |
|
Answer» `|(sin^2alphacos^2alpha,cosbetacos alpha,cosgammacos alpha+singammasin alpha),(cos alpha cos BETA+sinalphasin beta,cos^2beta+sin^2beta,cosgammacosbeta+singammasinbeta),(cosalphacosgamma+sinalphasingamma,cosbetacosgamma+sinbetasingamma,sin^2gamma+cos^2gamma)|` can be FACTORIZED into 2 determinant `|(cosalpha,sinalpha,x),(cosbeta,sinbeta,x),(cosgamma,singamma,x)||(cosalpha,cos beta,cos gamma),(sin alpha,sinbeta,sin gamma),(x,x,x)|=0`. |
|
| 7997. |
Find the moment of inertia about the x-axis of the figure bounded by two parabolas with dimensions indicated in. |
|
Answer» |
|
| 7998. |
Find the region on the Argand plane on which z satisfies1lt|z-2i|lt3 |
|
Answer» SOLUTION :Let`z=x+iy"The GIVEN inequality is "1lt|x+i(y-2)|LT 3` `implies1lt sqrt(x^2+(y-2)^2 lt 3` |
|
| 7999. |
Let X denote the sum of the numbers obtained when two fair dice are rolled. Find the variance and standard deviation of X. |
|
Answer» |
|
| 8000. |
Using the definition of definite integral as the limit of a sum evaluate int_(0)^(2)axdx where a is a constant. |
|
Answer» |
|