Explore topic-wise InterviewSolutions in .

This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.

7851.

If the common tangets of x^(2)+y^(2)=r^(2) and (x^(2))/(16)+(y^(2))/(9)=1 form a square, then the area (in sq. units) of the square is

Answer»

50
100
25
40

Answer :A
Discussion
7852.

Integrate the following functions : int(1+tanx)/(x+logsecx)dx

Answer»

`LOG(x+log SECX)+C`
`-log(x+log secx)+c`
`log(x-log secx)+c`
NONE of these

Answer :A
Discussion
7853.

Find the number of ways of selecting cricket team of eleven from 20 players such that at least one of Sachin and Dravid must be excluded

Answer»


ANSWER :`""^(20)C_(11)-"^(18)C_9`
Discussion
7854.

Let f(x)=3^(alphax)+3^(betax), where alpha ne beta and 3f'(x)log_(3)e=2f(x)+f''(x)(log_(3)e)^(2) for all x. Then the value of alpha+beta is :

Answer»


Solution :`f(X)=3^(alphax)+3^(betax)`
`f'(x)=alpha3^(alphax)ln3+3^(BETA x)beta ln 3`
`f''(x)=alpha^(2)3^(alphax)(ln3)^(2)+3^(betax)beta^(2)(ln3)^(2)`
PUT it in given CONDITION and solve.
Discussion
7855.

P(x) be połynomial of degree at most 5 which leaves remainders -1 and 1 upon division by (x-1)^(3) and (x+ 1)^(3) respectively. The sum of pairwise product of all roots (real and complex) of P(x) = 0 is

Answer»

`-5/3`
`-10/3`
2
`-5`

ANSWER :B
Discussion
7856.

Let ABC be an acute scalene triangle, and O and H be its circumcentreand orthocentre respectively. Further let N be the midpoint of OH. The value of the vector sum vec(NA)+vec(NB)+vec(NC is

Answer»

`vec(O)`(zero VECTOR)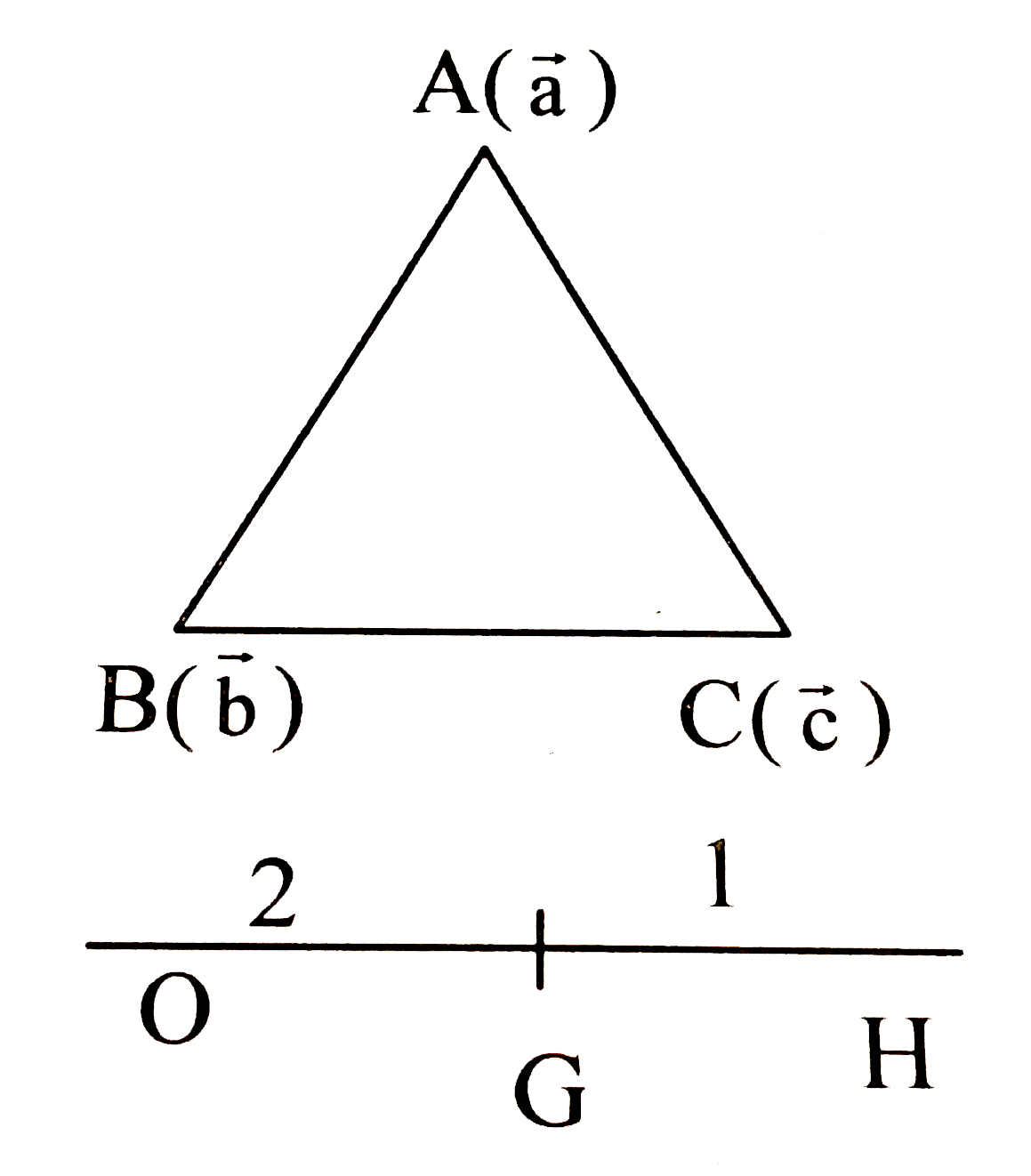
`vec(HO)`
`(1)/(2)vec(HO)`
`(1)/(2)vec(OH)`

Solution :CIRCUMCENTER (origin O )

`(vec(O))=((vec(a)+vec(b)+vec(C))/(3)),H=((vec(a)+vec(b)+vec(c))/(2))`
`vec(N)=(1)/(4)(veca+vec(b)+vec(c))`
Discussion
7857.

Obtain the inverse of the following matrix using elementary operations A=[{:(0,1,2),(1,2,3),(3,1,1):}]

Answer»


ANSWER :`=[{:((1)/(2),(-1)/(2),(1)/(2)),(-4,3,-1),((5)/(2),(-3)/(2),(1)/(2)):}]`
Discussion
7858.

Find all the values of the following (sqrt3+i)^(1//4)

Answer»


ANSWER :`2^(1/4)CIS(PI)/(24),2^(1/4)cis(13pi)/(24),2^(1/4)cis(25pi)/(24),2^(1/4)cis(37pi)/24)`
Discussion
7859.

If alpha,betaare the roots of quadratic equation x^2 + px + q = 0 and gamm deltaare the roots of x^2 + px — r = 0, then (a-gamma),(alpha - beta) is equal to :

Answer»


ANSWER :`-(q+r)`
Discussion
7860.

Integrate the functions (sin^(-1)sqrt(x)-cos^(-1)sqrt(x))/(sin^(-1)sqrt(x)+cos^(-1)sqrt(x)),x in[0,1]

Answer»


Answer :`(2(2x-1))/(pi)SIN^(-1)sqrtx+(2sqrt(x-x^(2)))/(pi)-x+C`
Discussion
7861.

The maximum number of normals that can be drawn to an ellipse/hyperbola passing through a given point is :

Answer»


ANSWER :4
Discussion
7862.

Let f(x)=a_(0)+a_(1)x+a_(2)x^(2)+……+a_(2n)x^(2n) and g(x)=b_(0)+b_(1)x+b_(2)x^(2)+….+b_(n-1)x^(n-1)+x^(n)+x^(n-1)+….x^(2n). If f(x)=g(x+1), then a_(n) in terms of n is equal to :

Answer»

`""^(2n+1)C_(n+1)`
`""^(2n-1)C_(n-1)`
`""^(2n-1)C_(n+1)`
`""^(n+1)C_(n+1)`

ANSWER :A
Discussion
7863.

A mango is dropped from rest from a height near the surface of earth.Wind is blowing horizontally and due to this wind an acceleration of 4 m//s^2 is generated in horizontal direction as well as gravitational acceleration. Path of the mango is :

Answer»




Discussion
7864.

Prove that 2 le (1+ (1)/(n))^(n) lt 3 for all n in N.

Answer»

Solution :LET `a_(n) = l(1+(1)/(n))^(n)`
For `n = 1, (1+1/n)^(n) = 2`
Now, `(1+1/n)^(n) = .^(n)C_(0) + .^(n)C_(1) (1/n) + .^(n)C_(2)(1/n)^(n) + "……." + .^(n)C_(r)(1/n)^(r ) + "……" + .^(n)C_(n)(1/n)^(n)`
` = 1+1+(n(n-1))/(2!) (1)/(n^(2)) + (n(n-1)(n-2))/(3!) = 1/(n^(3)) + "......"`
` + (n(n-1)xx"......"xx2xx1)/(n!) (1)/(n^(n)) "" (1)`
` = 2+(1)/(2!)(1-(1)/(n)) + (1)/(3!)(1+(1)/(n))(1-(2)/(n)) +"....."`
`+ (1)/(n!)(1-(1)/(n))(1-(2)/(n))"......"(1-(n-1)/(n))""(2)`
Hence, `a_(n) ge 2 ` for all `n in N`.
ALSO, `a_(n) LE 1 +1 + (1)/(2!) + (1)/(3!) + "....." + (1)/(r!) + "......" + (1)/(n!)`
Fo` 2 le r le n`, we have `r! = 1 xx 2 xx 3 xx "......" xx r ge 2^(r-1)`.
`:. a_(n) le 1 + 1 + 1/2 + 1/(2^(2))+ "......" + (1)/(2^(r-1))+"....."+(1)/(2^(n-1))`.
` = 1+(1-(1//2)^(n))/(1-(1//2))`
` = 1+2(1-1/(2^(n))) = 3 - (1)/(2^(n-1))`
`:. a_(n) le 3 - 1/(2^(n-1)) lt 3 AAn ge 1`
Discussion
7865.

Two concentric ellipse be such that the foci of one be on the other and if 3/5 and 4/5 be their eccentricities. If theta be the angle between their axes, then the values of 2(1+sin^(2)theta+sin^(4)theta) must be

Answer»


ANSWER :6
Discussion
7866.

Identify the quantifier in the statement and write the negation of the statement. For every real number x,x+4 is greater than x.

Answer»

SOLUTION :There EXISTS a REAL X,x+4 is not GREATER than x.
Discussion
7867.

If the circle x^(2) + y^(2) -4x + 6y + a =0 has radius 4, find a.

Answer»


ANSWER :a=-3
Discussion
7868.

the value of1/8 (3-4 cos2 theta+ cos4 theta) is

Answer»

`COS4 THETA `
` SIN4 theta `
` sin^4 theta `
`cos^4theta`

ANSWER :C
Discussion
7869.

Nerve impulse for hearing originates in :

Answer»

EAR drum
Auditory NERVE
Reissner's membrane
Organ of corti

Answer :A
Discussion
7870.

Two ships leave a port from a point at the same time. One goes with a velocity of 3kh/h along North-East making an angle of 45^(@) with East direction and the other travels wth a velocity of 4km/h along South-East making an angle of 15^(@) with East direction. Then, the distance between the ships at the end of two hours is

Answer»

`2sqrt13`
`SQRT13`
5
10

Answer :A
Discussion
7871.

The plane passing through (5,1,2) and perpendicular to the line 2(x-2) y - 4 = z-5 meets the line in the ............. Point.

Answer»

(1,2,3)
(2,3,1)
(1,3,2)
(3,2,1)

ANSWER :A
Discussion
7872.

The term independent of x in (1+x+x^(-2)+x^(-3))^(10)is n then the last digit of (n+2)^(n)is

Answer»

1
3
7
9

Solution :`(1+x(1)/(x^(2))+(1)/(x^(3)))^(10)=((x+x+x^(3)+x^(4))^(10))/(x^(30))`
Coefficient of `x^(30)` in `(1+x+x^(3)+x^(4))^(10)=(1+x)^(10)(1+x^(3))^(10)`
`=.^(10)C_(10).^(10)C_(0).^(10)C_(3)+.^(10)C_(6)+.^(10)C_(7).^(10)C_(9)`
`=1+1200+9450+1200`
`=11851`
LAST digit of `(11853)^(11851)=7`
Discussion
7873.

Consider the shown arrangement where the blocks A and B connected by means of a uniform string is being moved vertically up[ by the force F. Each block weighs 2 kg while the mass of sting is 500 gm. The tension at midpoint of the string (in N) equals_______.

Answer»


ANSWER :27.00`
Discussion
7874.

Equation of a line through the points (0, 0, 0) and (1, 2, 3) is

Answer»

`(x-1)/(1)=(y-1)/(2)=(z-1)/(3)`
`(x-1)/(1)=(y-2)/(2)=(z-3)/(3)`
`(x-2)/(1)=(y-2)/(2)=(z-2)/(3)`
`(x-3)/(1)=(y-3)/(2)=(z-3)/(3)`

ANSWER :B
Discussion
7875.

Evaluate underset(0)overset(pi//2)int sin^(5)x cos^(4)x dx

Answer»


ANSWER :`(8)/(315)`
Discussion
7876.

An unbounded feasible region

Answer»

admits BOUNDED feasible solution
admits UNBOUNDED solution
may admit bounded as well as unboundedfeasible solutoin
none of these

ANSWER :C
Discussion
7877.

Let A and B be two matrices (neither null nor singular ) with real entries . Match the statement given in list-I with a condition given inList-ii (HereI represents a suitable identity matrix)

Answer»

<P>`{:(P,Q,R,S),(4,2,3,1):}`
`{:(P,Q,R,S),(2,1,4,3):}`
`{:(P,Q,R,S),(1,3,2,4):}`
`{:(P,Q,R,S),(2,4,1,3):}`

ANSWER :D
Discussion
7878.

Prove the following : [[x+4,2x,2x],[2x,x+4,2x],[2x,2x,x+4]]-(5x+4)(4-x)^2

Answer»

SOLUTION :`[[x+4,2X,2x],[2x,x+4,2x],[2x,2x,x+4]]`
`[R_1rarrR_1+R_2+R_3]`
`[[5x+4,5x+4,5x+4],[2x,x+4,2x],[2x,2x,x+4]]`
=`(5x+4)[[1,1,1],[2x,x+4,2x],[2x,2x,x+4]]`
`[C_2rarrC_2-C_1,C_3rarrC_3-C_1]`
=`(5x+4)[[1,0,0],[2x,4-x,0],[2x,0,4-x]]`
=`(5x+4)(4-x)^2`
Discussion
7879.

If p:2 plus 3 is five and q: Delhi is the capital of India are two statements, then the statement "Delhi is the capital of India and it is not that 2 plus 3 is five" is

Answer»

`~PVVQ`
`~p^^q`
`p^^~q`
`pvv~q`

ANSWER :B
Discussion
7880.

Prove that |{:(1+a^(2)-b^(2),2ab,-2b),(2ab,1-a^(2)+b^(2),2a),(2b,-2a,1-a^(2)-b^(2)):}|=(1+a^(2)+b^(2))^(3)

Answer»

`(1+a^(2)+B^(2))^(3)`
`(1-a^(2)-b^(2))`
`1+a+b`
`(1+a+b)^(2)`

ANSWER :A
Discussion
7881.

Find area of the triangle withh vertices at the point given in each of the following : (5,4),(2,5),(2,3)

Answer»


ANSWER :3
Discussion
7882.

Evaluate the following definite integrals as limit of sums. int_(1)^(4)(x^(2)-x)dx

Answer»


ANSWER :`(27)/(2)`
Discussion
7883.

Solve x^(5)-3x^(3)+2x^(2)-3 gt0.

Answer»

`(-OO,-0.87)`
`(-1.90,-0.87)`
`(-1.90,-0.87)cup(1.58,oo)`
`(-0.87,1.58)`

Solution :GRAPH the function, and determine that the three ZEROS are -1.90,-0.87, and 1.58. the PARTS of the graph that are above the x-axis have x-coordinates between -1.90 and -0.87 and are larger than 1.58.
Discussion
7884.

Find the maximum profit that a company can make, if the profit function is given byp(x)=41-72x-18x^(2)

Answer»


ANSWER :113 UNITS
Discussion
7885.

Find the equation of common chord of the following pair of circlers (x-a)^(2)+(y-b)^(2)=c^(2),(x-b)^(2)+(y-a)^(2)=c^(2)(a!=b)

Answer»


ANSWER :`x-y=0`
Discussion
7886.

Let A = [(2,-1),(3,4)], B = [(5,2),(7,4)] , C = [(2,5),(3,8)] . Let D be a matrix such that CD = AB then D equals

Answer»

I
O
`-A`
NONE of these

Answer :D
Discussion
7887.

show that the matrix A= [[1,-1,5],[-1,2,1],[5,1,3]] is a symmetric matrix

Answer»

SOLUTION :`A^T = [(1,-1,5),(-1,2,1),(5,1,3)] = A THEREFORE A` is SYMMETRIC
Discussion
7888.

If overline(a)=hat(i)+hat(j), overline(b)=hat(j)+hat(k), overline(c)=alphaoverline(a)+betaoverline(b) and the vectors hat(i)-2hat(j)+hat(k), 3hat(i)+2hat(j)-hat(k), overline(c) are coplanar, then (alpha)/(beta)=

Answer»

`0`
`-2`
`-3`
`-1`

ANSWER :C
Discussion
7889.

By examining the chest X-ray, probability that T.B is detected when aperson is actually suffering is 0.99. theprobability that the doctor diagnoses incorrectly that a person has T.B. onthe basis of X-ray is 0.001. in a certain city 1 in 100 personssuffers from T.B. A person is selected at random is diagnosed to have T.B.What is the chance that he actually has T.B.?

Answer»

SOLUTION :LET `E_(1)`=Event that PERSON has TB
`E_(2)`=Event that peron does not have TB
E=Event that the person is DIAGNOSED to have TB
`thereforeP(E_(1))=1/1000=0.001,P(E_(2))=999/1000=0.999`
and `P(E//E_(1))=0.99and P(E//E_(2))=0.001`
`therefore P(E_(1)//E)=(P(E_(1)cdotP(E//E_(1))))/(P(E_(1))cdotP(E//E_(1))+P(E_(2))cdotP(E//E_(2)))`
`=(0.001xx0.99)/(0.001xx0.99+0.999xx0.001)`
`=(0.000990)/(0.000990+0.000999)` ltbr gt`=990/1989=110/221`
Discussion
7890.

Evaluate Lt_(x to oo)(11 x^3 - 3x + 4)/(13x^3 - 5x^2 - 7)

Answer»


ANSWER :A::C
Discussion
7891.

If A(3, -2, 2) and B(2, 9, 5) are end points of a diameter of a circle, then points C(5, 6, -1)

Answer»

is CENTRE of the CIRCLE
lies on the CIRCUMFERENCE of the circle
lies outside the circle
lies inside the circle

Answer :B
Discussion
7892.

int_(3)^(5)(t^(2))/(t^(2)-4)dx=.............

Answer»

`2-log((14)/(15))`
`2+log((15)/(7))`
`2+log((14)/(15))`
0

Answer :B
Discussion
7893.

If degree of polynomal obtained in previous question is p and (p-5) + sin x_(5) cos x tan x are G.P then cos^(9) x+ cos^(6) x + 3 cos^(5) x-1=

Answer»

`-1`
0
1
none of these

Answer :B
Discussion
7894.

Theremainderobtainedwhen1!+ 2!+3!+….. + 11 !isdivided by 12is

Answer»

9
8
7
6

Answer :A
Discussion
7895.

If int_(0)^(1)(dx)/( (1+ x) (2+x) sqrt(x (1-x)) )= pi A then A is equal to ( sqrt(2) = 1.41, sqrt(3) = 1.73)

Answer»


ANSWER :`0.30`
Discussion
7896.

The numerically greatest term in the expansion of (3+2x)^(49) when x=1//5 is…..

Answer»

4TH term
5th term
6th term
7th term

Answer :C
Discussion
7897.

Vapour density of a gas is 22. What is its molecular mass ?

Answer»

33
22
44
11

Answer :A
Discussion
7898.

Choose the correct answer int x^2e^(x^3) dx =

Answer»

`1/3 E^(x^3)+C`
`1/3 e^(x^2)+c`
`1/2 e^(x^3)+c`
`1/2 e^(x^2)+c`

ANSWER :A
Discussion
7899.

If R is a relation on Z defined by xRy iff x divides y then R is

Answer»

REFLEXIVE and symmetric
reflexive and TRANSITIVE
symmetric, transitive
EQUIVALENCE

ANSWER :B
Discussion
7900.

Which of the following functions is increasing in (0 , oo) ?

Answer»

`E^(X)`
`(1)/(x)`
`-x^(2)`
`x^(-2)`

ANSWER :A
Discussion