InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 7801. |
If y = mx + 6 is a tangent to the hyperbola he parabola y^(2) = 4ax, then the length ofthe latus rectum of the parabola is |
|
Answer» `6sqrt(17/20)` |
|
| 7802. |
The slopes of the lines which make an angle 45^(@) with the line 3x - y = -5 are |
|
Answer» 1, -1 |
|
| 7804. |
Find the sum upto n termsofthe series 1*4*7*10*13*16+"....". |
|
Answer» SOLUTION :Let `T_(n)` be the nth term of the given series. ` therefore T_(n)=(" nth term of " 1,4,7, "..."(" nth term of " 4,7,10,"......")` `(" nth term of " 7,10,13, "...")(" nth term of " 10,13,16,"......")` `T_(n)=(3n-2)(3n+1)(3n+4)(3n+7)""".........(i)"` ` therefore V_(n)=(3n-2)(3n+1)(3n+4)(3n+7)(3n+10)` `V_(n-1)=(3n-5)(3n-2)(3n+1)(3n+4)(3n+7)` `impliesV_(n)=(3n+10)T_(n) "" [" from Eq. (i) "]` and ` V_(n-1)=(3n-5)T_(n)` `therefore V_(n)-V_(n-1)=15T_(n)` `therefore T_(n)=(1)/(15)(V_(n)-V_(n-1))` `therefore S_(n)=sumT_(n)=sum_(n=1)^(n)(1)/(15)(V_(n)-V_(n-1))` `=(1)/(15)(V_(n)-V_(0)) "" [" from important Theorem 1 of " SUM]` `=(1)/(15){(3n-2)(3n+1)(3n+4)(3n+7)(3n+10)-(-2)(1)(4)(7)(10)}` `=(1)/(15){(3n-2)(3n+1)(3n+4)(3n+7)(3n+10)+560}` Shortcut Method `S_(n)=(1)/(" last factor of III term - first factor of I term ")` ( Taking ONE extra factor in `T_(n)` in last - Taking one exra factor in I term in start ) `=(1)/((16-1)){(3n-2)(3n+1)(3n+4)(3n+7)(3n+10)-(-2)*1*4*7*10}` `=(1)/(15){(3n-2)(3n+1)(3n+4)(3n+7)(3n+10)+560}` |
|
| 7805. |
A beg contains 4 red and 4 black , another bag contains 2 red and 6 black balls. One of the two bags is selected at random and a ball is drawn from the bag which is found to be red. Find the probability that the ball is drawn from the first bag. |
|
Answer» |
|
| 7806. |
Solution of differential equation f^(')(x)f^(''')(x)=3(f^('')(x))^(2),(y=f(x)) is: |
|
Answer» `x=k_(1)y^(2)+k_(2)y+k_(3)` `(3f^('')(x))/(F^(')(x))=(f^(''')(x))/(f^('')(x))` `implies3hInf^(')(x)=f^('')(x)+k` `implies(d^(2)x)/(dy^(2))=C` |
|
| 7807. |
If b be the p^(th)term of G.P. where (p+q)^(th)and (p - )^(th)terms are a and c respectively and if f(x)=ax^(2)+2bx+c,then for all x in R |
|
Answer» `af(X)=0` |
|
| 7808. |
Check the injective and surjective of the following functions : f : Z rarr Z given by f(x) = x^2 |
|
Answer» Solution :We have `f(-1) = (-1)^2 = 1` and `f(1) = 1^2 =1 ` `THEREFORE` f maps both -1 and 1 to 1 `therefore ` f is not injective Since SQUARE of an integers can.t EXIST an integer X satisfying `x^3 = -1 ` `therefore,` f is not a subjective |
|
| 7809. |
Find the parametric form of vector equation, and Cartesian equations of the plane containing the line vecr=(hati-hatj+3hatk)+t(2hati-hatj+4hatk) and perpendicular to plane vecr*(hati+2hatj+hatk)=8. |
|
Answer» |
|
| 7810. |
Let S={(x,y):abs(abs(absx-2)-1)+abs(abs(absy-2)-1)=1). If S is made out of wire, then the length of wire required is |
|
Answer» `16sqrt2` |
|
| 7811. |
Translate "Chinu and Minu went to Calcutta, but Minu came back earlier since she lost all her money" propositions into symbolic form, stating the prime components |
|
Answer» Solution :Let p:The Government can solve the unemployment PROBLEM. Q :Public opinion will rise against it. `:.` ANSWER is `(p rarrq ) rarrr`. |
|
| 7812. |
The vector equation of the line, whose cartesian equation is (x-3)/(2)=(y+4)/(5)=(z-6)/(3) is |
|
Answer» `BARR=(3hati-4hatj-6hatk)+LAMBDA(2hati-5hatj+3hatk)` |
|
| 7813. |
(0,-1) and (0, 3) are two opposite vertices of a square. The other two vertices are... |
|
Answer» (0, 1), (0, -3) |
|
| 7814. |
Find the value of k, so that the length of the subnormal at any point on the curve xy^(k)=a^(k+1) is a constant. |
|
Answer» |
|
| 7815. |
Integrate the function in Exercise. e^(x)((1)/(x)-(1)/(x^(2))) |
|
Answer» |
|
| 7816. |
Let V_(r) denotes the sum of the first r terms of A.P. whose first term is r and the common difference is (2r-1). Let T_(r)=V_(r+1)-V_(r)-2 and Q_(r)=T_(r+1)-T_(r) for r = 1, 2 ………… Which one of the following is a correct statement |
|
Answer» `Q_(1),Q_(2),Q_(3)`…………are in AP with common DIFFERENCE 5 |
|
| 7818. |
Differentiate tan^2x+a^x |
|
Answer» SOLUTION :`y=tan^2x+a^x` `dy/dx=2tanxcdot sec^2x+a^xcdotlna` |
|
| 7819. |
Evaluate the determinants below in examples number 1 and 2 |{:(costheta,-sintheta),(sintheta,costheta):}| |
|
Answer» |
|
| 7820. |
Let f(x)=[x] where [x] be the greatest integer less than or equal to x. g(x)={{:(0,","x inZ),(x^2,"," x in R-Z):} z is the set of integers , phi(x)=fog(x) and Psi(x)=gof(x). Then on the set R-Z . |
|
Answer» both `PHI` and `Phi` are CONTINUOUS |
|
| 7821. |
Find the area of the triangular region boundedby the sides y = 2x + 1, y = 3x + 1 andx = 4 |
|
Answer» |
|
| 7822. |
A bag contains 5 balls of unknown colours. A ball is drawn at random from it and is found to be red. Then the probability that all tha balls in the bag are red, is |
| Answer» Answer :D | |
| 7823. |
The normals at three points P,Q,R of the parabola y^(2)=4axmeet in (h.k) . The centroid of triangle PQR lies on |
|
Answer» x=0 |
|
| 7824. |
Let **' be the binary operation on N given by a**'b= L.c.m. of a and b. Find 5**7, 20**16 |
|
Answer» Solution :`5**7`= L.c.m of 5 and 7=35 `20**16`=L.c.m of 20 and 16 =80` |
|
| 7825. |
If f(x)={:(,(sin (1+[x]))/(x),"for "[x] ne 0),(,0,"for [x]=0"):} where [x] denotes the greatest integer not exceeding x then underset(x to0-)"Lt" f(x)= |
|
Answer» `-1` |
|
| 7826. |
Bag I contains 3 red and 4 black balls. While Bag II contains 5 red and 6 black balls. One ball is drawn at random from one of the bags and it is found to be red. Find the probability that it was drawn from Bag II. |
|
Answer» |
|
| 7827. |
If sinA+sinB=a and cosA+cosB=b, show that sin(A+B) = (2ab)/(b^2+a^2) |
|
Answer» SOLUTION :`sin(A+B)=(2TAN((A+B)/2))/(1+tan^2((A+B)/2)` = `((2a)/b)/(1+a^2/b^2) = ((2a)/b)/((b^2+a^2)/b^2) = (2ab)/(b^2+a^2)` |
|
| 7828. |
Find the mean deviation from the mean for the set of obervations 1,2,3. |
|
Answer» |
|
| 7829. |
Express tan^(-1)((cosx)/(1-sinx)),-(3pi)/2ltxltpi/2 in the simplest form. |
|
Answer» |
|
| 7830. |
Let X and Y be the sets of all positive divisors of 400 and 1000 respectively ( including 1 and the number). Then n(XcapY)= |
|
Answer» 4 |
|
| 7831. |
The values of a for which the function f(x)=sin x - ax + b increases on R are ………….. |
|
Answer» |
|
| 7832. |
Amy drove the 200 miles to New Orleans at at average speed 10 miles per hour faster than her usual average speed. If the complwrws the trip in 1 hour less than usual, what is her usual driving speed, in miles per hour? |
|
Answer» 20 |
|
| 7833. |
If a.hati=4 then (axx hatj).(2hatj-3hatk) is equal to |
|
Answer» 12 `=a.{-3(hat(j)xxhat(k))}=-3(a.hat(i))` `=-12""[ :' a.hat(i)=4," given"]` |
|
| 7834. |
Find the number of ways to arrange 8 persons around circular table if never sit together |
|
Answer» |
|
| 7835. |
If (d)/(dx)((1+x^2+x^4)/(1+x+x^2)) = a+bx, find the values of a and b . |
|
Answer» |
|
| 7836. |
One atom of an element x weigh 6.643 xx 10^(-23) g. Number of moles of atom in 20 kg is :- |
|
Answer» 4 |
|
| 7837. |
Find int(xsin^(-1)x)/(sqrt(1-x^(2)))dx |
|
Answer» `X + SQRT(1 -x^(2)) SIN^(-1) x + C ` |
|
| 7838. |
The smallest natural number 'n' for which n!lt((n+1)/2)^(n) holds is |
|
Answer» 1 |
|
| 7841. |
Five cities A,B,C,D,E are connected to each other by straight roads. What is the total number of such roads? |
|
Answer» Solution :FIVE cities A, B, C, D, E are connected to each other by straight roads. `:.` The number of such ROSES is `(""^5P_2)/(2!)=10.` |
|
| 7842. |
If Integration using trigonometric identities : int(cos 8x+1)/(tan2x-cot 2x)dx=acos 8 x+c then a=.......... |
|
Answer» `-(1)/(16)` |
|
| 7843. |
Equation of the tangent at a point P on the parabola y^(2)=4ax, the normal at which is at a distance a sqrt5//4 from the focus of the parabola is |
|
Answer» `4x-2y+a=0` |
|
| 7844. |
The members of a consulting firm rent cars from three agencies: 50% from agency X, 30% from agency Y and rest from agency Z. From past experience it is known that 9% of the cars from agency X need a service and tuning before renting, 12% of the cars from agency Y need a service and tuning before renting and 10% of the cars from agency Z need a service and tuning before renting. If the rental car delivered to the firm needs service and tuning, find the probability that agency Z is not to be blamed. |
|
Answer» |
|
| 7845. |
Let f(X)=In (2x -x^2)+ sin (pix)/(2). Then which one of the following options is not correct? |
|
Answer» Also `f(1+alpha)=f(1-alpha)for all alpha in (0,1)` So ,y =f (x) is symmetircal about the line x=1 Clearly `2 x-x^2` and SIN `(pix)/(2)` attain the maximum value 1 at x=1 Therefore `f(x)=In(2x-x^2)+sin (pix)/(2)` attains its maximum value at x=1 .Also We OBSERVE that `f(x) rArr - oo as x rArr 0^(+) or x rArr2^(-)` minmum values of the function f(x) does not EXIST HENCE ,option (b) is not correct |
|
| 7846. |
Find the second order derivatives of the functions given in Exercises 1 to 10. x^(2)+3x+2 |
|
Answer» |
|
| 7847. |
A fruit grower canuse two types of fertilizer in his garden brand P and brand Q. The amounts (in kg) of nitrogen phosphoric acid, potash, and chlorine a bag of each brand are given in the stable. Tests indicate that the garden needs at least 240kg of phosphoric acid, at least 270 kg ofpotash and at most 310 kg of chlorine. If the grower wants to minimise the amount of nitrogen added to the garden, how many bags of each brand should be used? What is the minimum amount of nitrogen added in the garden? |
Answer» Solution :Let `x` bags of brand `P` and `y` of brand `Q` are used by fruit grower. 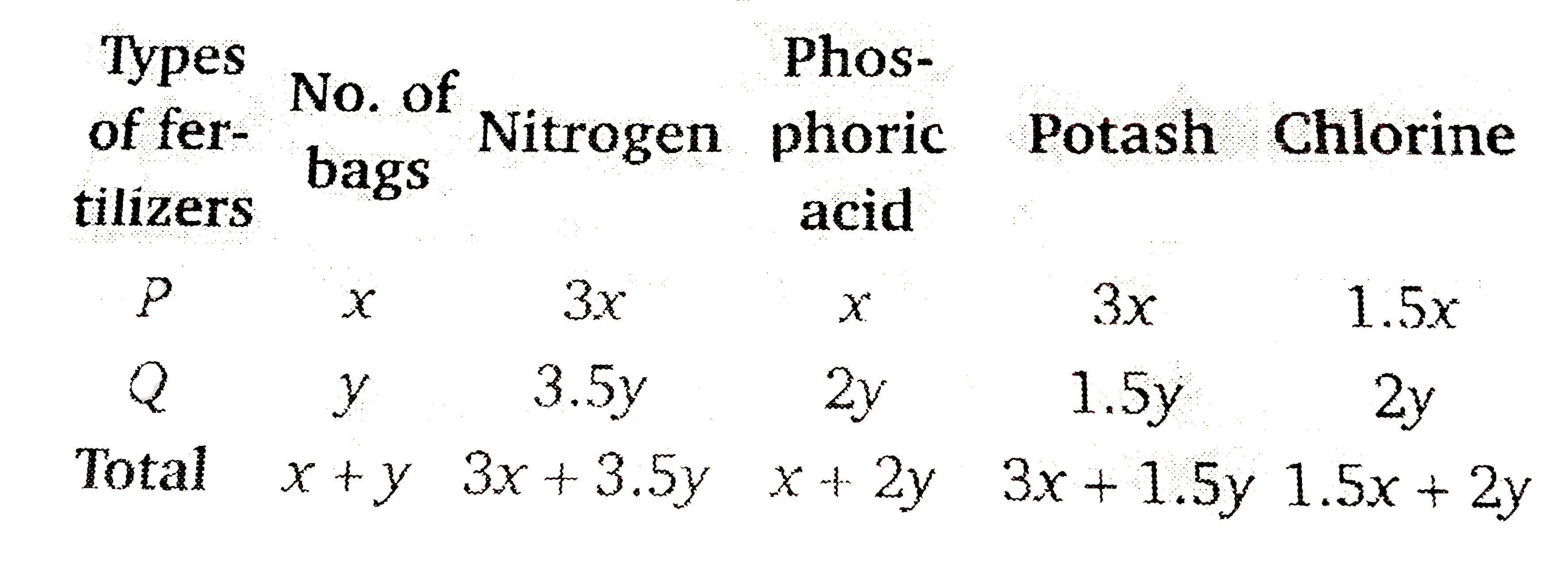 Minimise `Z=3x+3.5y`……………1 and constraints `x+2yge240`………………2 `3x+1.5yge270`………………….3 `1.5x+27le310`……………..4 `xge0,yge0`.......................5 FIRST DRAW the graph of the line `x+2y=240`  Put `(0,0)` in the inequation `x+2yge240` `0+2xx0ge240implies0ge240` (False) Thus, the half plane does not contain origin. Now, draw the graph of the line `3x+1.5y=270` 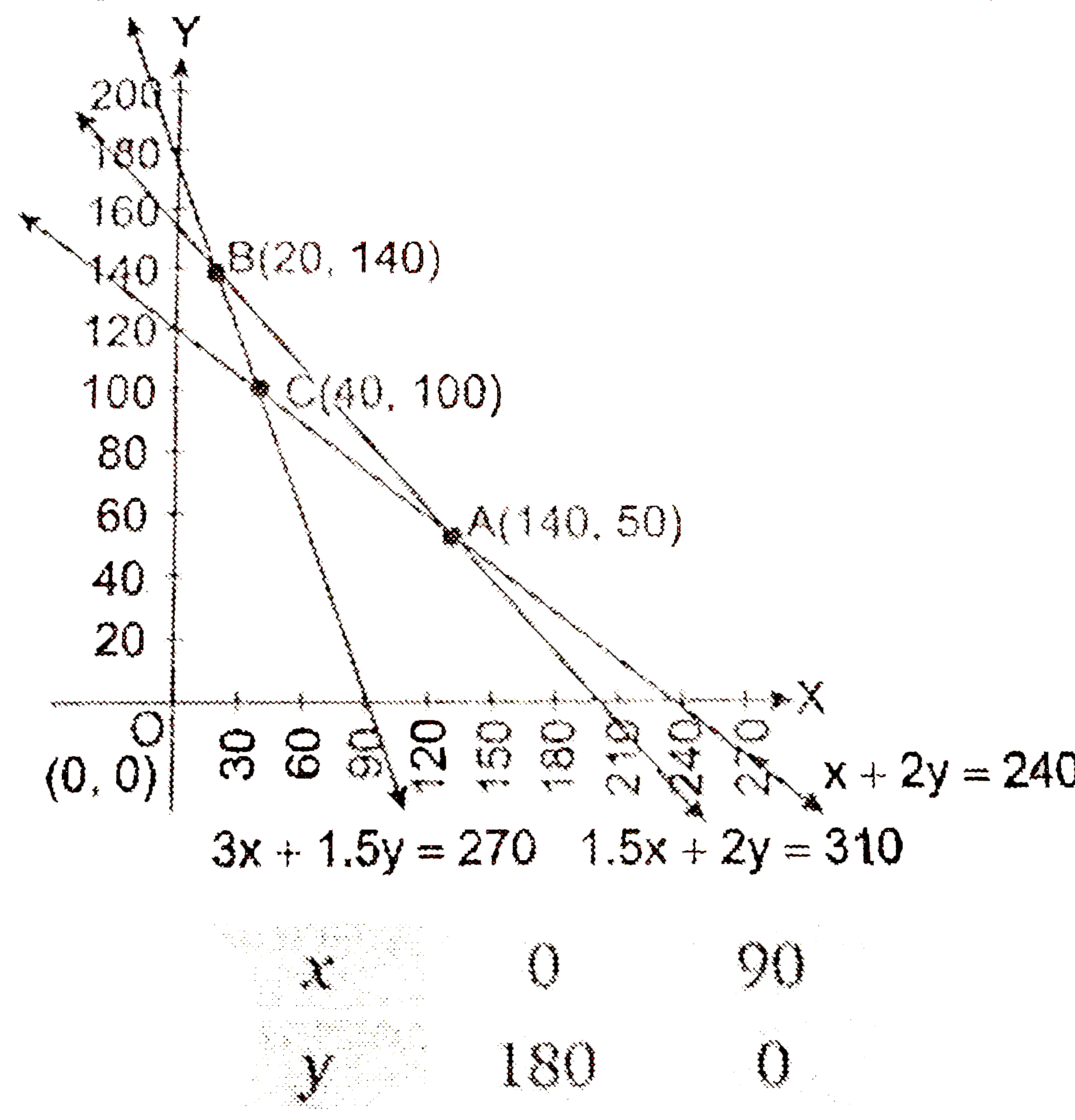 Put `(0,0)` in the inequations `3x+1.5yge270` `3xx0+1.5xx0ge270implies0ge270` (False) Thus, the half plane does not contain origin. Now, draw the graph of the line `1.5x+2y=310` 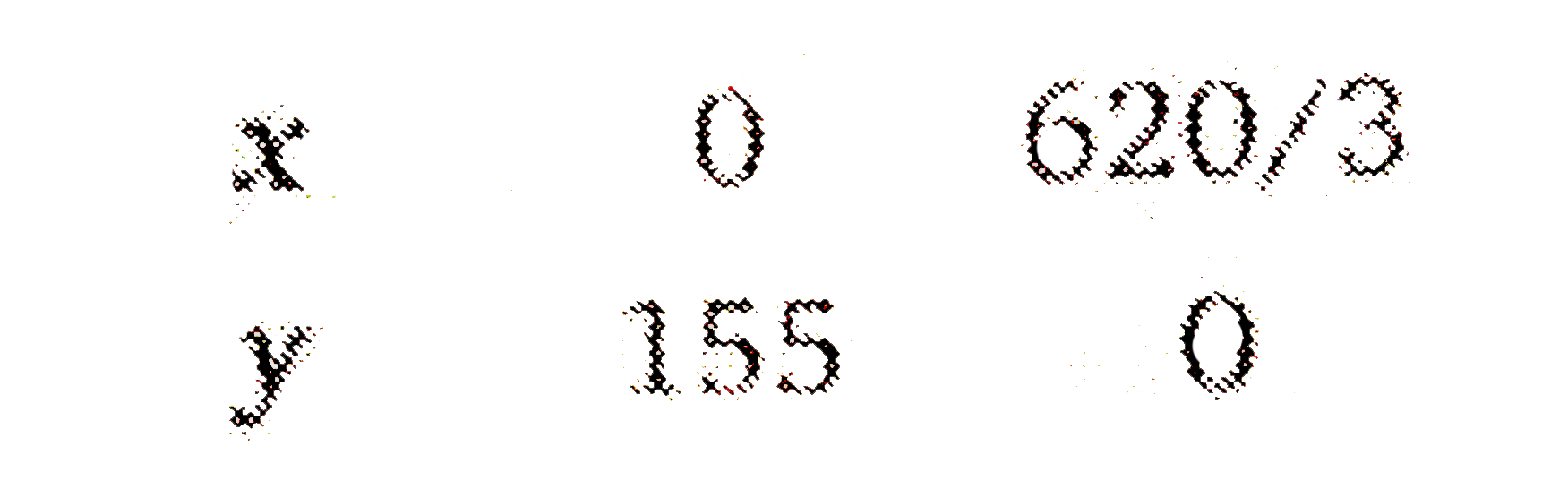 PUt `(0,0)` in theinequation `1.5x+2yle310` `1.5xx0+2xx0le310implies0le310` (True) Thus, the half plane does not contain origin. Since `x,yge0` So the feasible region will be in first quadrant. The point of intersection of equations `1.5x+2y=310` and `x+2y=240` is `A(140,50)`. Similarly the point of intersection of the equation `3x+1.5y=270` and `1.5x+2y=310` is `B(20,140)`. `:.` Feasible region is ABCA. It vertices are `A(140,50),B(20,140)` and `C(40,100)` at which we find the value of `Z`.  Therefore, the minimum value of `Z` is 470 at point `C(40,100)`. Minimum nitrogen to be MIXED in GARDEN is 470 kg for which 40 bags of brand `P` and 100 bats of brand `Q` should be used. |
|
| 7848. |
Prove that if to each element of any row or column of a determinant, the equimultiples of corresponding elements of other row (or column) are added, then value of determinant remains the same. |
|
Answer» |
|
| 7849. |
Find the Quantifiers There exists an even prime number other than 2. |
| Answer» SOLUTION :There EXISTS | |
| 7850. |
Which of the following is true Statement-I : int_(0)^(2pi) sqrt((1-cos2x)/(2)) dx=4 Statement-II : int_(-1)^(1) log((1+x)/(1-x))dx= 2 int_(0)^(1) log (1+ x)/(1-x)dx |
|
Answer» Only I |
|