InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 8451. |
Solve -12x gt 30, when i.x is a natural number. ii.x is an integer. |
|
Answer» II. The i.solution set of INEQUALITY is {………..-6, -5, -4, -3} |
|
| 8452. |
Find the number of different seven digit numbers that can be written using only the three digits, 1,2,3 with the condition that the digit 2 occurs atleast 2 times in each number. |
|
Answer» |
|
| 8453. |
A variable line 'L' Passing through the origin cuts two parallel lines x-y+10=0 and x-y+20=0 at two points A and B respectively . If P is a point on line 'L' such that OA , OP, OB are in harmonic progression then the locus of P is |
|
Answer» 3x+3y+40=0 |
|
| 8454. |
Integrate the following functions. int(x^(3))/(2x+1)dx |
|
Answer» |
|
| 8455. |
A: If the transformed equation of a curve is 9X^(2) + 16Y^(2) = 144 when the axes are rotated through an angle 45^(@), then the original equation is 25x^(2) - 14xy+ 25y^(2) = 288. R: If f(x,y)=0 is the transformed equation of a curve when the axes are rotate through an angle theta then the original equation of the curve is f(x cos theta + y sin theta, -x sin theta + y cos theta)=0 |
|
Answer» Both A and R are true and R is the correct EXPLANATION of A. |
|
| 8456. |
int cos sqrt(x)dx= |
|
Answer» `2 [ SQRT(X) SIN sqrt(x) + cossqrt(x) ] + c ` |
|
| 8457. |
If y = (a^(cos x))/( sqrt(1+ x^(2) )),then (dy)/(dx) = |
|
Answer» ` (a^(cos x ) (( 1+x^(2) )(LOG a)(sin a )(sin x) ))/( (SQRT( 1+ x^(2)))^(3)) ` |
|
| 8458. |
IfA_n= [ad ]A_2 =[{:( a_2, a_s),( a_4 .a_5):}], A_5 =[{:( a_6,a_7,a_8),( a_9,a_10 ,a_11),( a_12,a_13,a_14):}]= A_n =[…]and so on , where a_r= [log _2 r] where [.] denotes greatest integer function ) .Then T_r (A_10 )is equal to ,(T_r stands for trace of teh matrix ) |
|
Answer» 800 |
|
| 8459. |
Evaluate int_(0)^(1) x e^(x^(2))dx. |
|
Answer» |
|
| 8460. |
The solution of linear programming problem, maximize Z=3x_(1)+5x_(2) subject to 3x_(1)+2x_(2) le 18, x_(1) le 4, x_(2) le 6, x_(1) ge 0, x_(2) ge 0 is ……….. |
|
Answer» `x_(1)=2, x_(2)=0, z=6` |
|
| 8461. |
Two distinct numbers are chosen from 1,3,5,7 ……. 151,153,155 and multiplied . The probability that the product is a multiple of 5 is |
|
Answer» `1020/3003` |
|
| 8462. |
How many different numbers each of the six digit can be formed using the digit 1,2,1,2,3,3, ? |
|
Answer» 90 |
|
| 8463. |
The perpendicular distance of the point (3, -4, -5) from the line (x-2)/(4)=(y+6)/(5)=(z-5)/(-3) is …..... |
|
Answer» `1/5sqrt(1657)` |
|
| 8464. |
A curve is defined by the condition that the sum of the x and y intercepts of its tangents is always equal to 2. Express the condition by means of a differential equation. |
|
Answer» |
|
| 8466. |
If the transversal y = m_(r)x: r = 1,2,3 cut off equal intercepts on the transversal x +y = 1 then 1 +m_(1),1 +m_(2),1+m_(3) are in |
|
Answer» A.P. Thus the POINTS of intersection of the three lines on the TRANSVERSAL are `P ((1)/(1+m_(1)),(m_(1))/(1+m_(1))), Q ((1)/(1+m_(2)),(m_(2))/(1+m_(2)))` and `R((1)/(1+m_(3)),(m_(3))/(1+m_(3)))` According to QUESTION `PQ = QR` `((1)/(1+m_(1))-(1)/(1+m_(2)))^(2)+((m_(1))/(1+m_(1))-(m_(2))/(1+m_(2)))^(2)` `= ((1)/(1+m_(2))-(1)/(1+m_(3)))^(2) +((m_(2))/(1+m_(2))-(m_(3))/(1+m_(3)))^(2)` `rArr (m_(2)-m_(1))/(1+m_(1)) = (m_(3)-m_(2))/(1+m_(3))` `rArr (1+m_(2))/(1+m_(1)) - 1 = 1 -(1+m_(2))/(1+m_(3))` `rArr (1+m_(2))/(1+m_(1)) +(1+m_(2))/(1+m_(3)) =2` `rArr 1+m_(2) =(2(1+m_(1))(1+m_(3)))/((1+m_(1))+(1+m_(3)))` `rArr 1+m_(1), 1 +m_(2), 1 +m_(3)` are in H.P. |
|
| 8467. |
Ifu = sqrt( a^2cos^2 theta+b^2 sin ^2theta ) + sqrt( a^2 sin^2 theta+b^2 cos^2theta ) then thedifferencebetweenthe maximumand manimumvaluesofu^2is givenby |
|
Answer» `(a+b)^2` |
|
| 8468. |
If the letters of the word SACHIN are arranged in all possible ways and these words are written out as in dictionary, then the word SACHIN appears at serial number |
|
Answer» 602 |
|
| 8469. |
State whether the following statements are true or false, Justify. If ** is a commutative binary opertion on N, then a ** (b **c) = (c**b) **a |
| Answer» | |
| 8470. |
Integrate the following functions. int(x^(2)+a^(2))/(x^(4)+a^(4))dx |
|
Answer» |
|
| 8471. |
A and B are among 30 persons who sit at random along a round table. Find the probability that there are any six persons between A and B . |
|
Answer» |
|
| 8472. |
Which of the following is CORRECT combination ? |
|
Answer» `(II) (ii) (S) ` |
|
| 8473. |
Which of the following is CORRECT combination ? |
|
Answer» `(II) (ii) (R )` |
|
| 8474. |
Which of the following is CORRECT combination ? |
|
Answer» `(IV) (II) (S)` |
|
| 8475. |
Axes are co-ordinate axes, S and S^(1)are Foci, B and B^(1)are the ends of minor axis|SBS^(1) = sin ^(-1) ((4)/(5) ) .if area of SB S^(1) B^(1)is 20sq. Units then eq. of the ellipse is |
|
Answer» A) ` (X^(2) )/( 20 ) + ( y^(2))/( 16) =1` |
|
| 8476. |
Solve the following differential equation:xy(dy)/(dx)-y^2=(x+y)^2e^(-y//x) |
|
Answer» |
|
| 8477. |
If the the angle between the circles x^2+y^2-12x-6y+41=0 andx^2+y^2+kx+6y-59=0 is 45^@ find k. |
|
Answer» |
|
| 8478. |
Evaluate the following integrals (iv) int_(-1)^(1)(x^(4)+sin^(3)x)dx |
|
Answer» |
|
| 8479. |
Draw the graph of y=sin^(-1)(sin x) |
|
Answer» SOLUTION :`y = SIN^(-1) (sin X)` `rArr""sin y = sin x` `rArr""y=npi+(-1)^(n)x, n in Z` Now `y in [-pi//2, pi//2] ` so we have the following table for values for values of x and y.  From the above informations, we can PLOT the graph of `y=sin^(-1)(sin x)` as shown in the following figure. 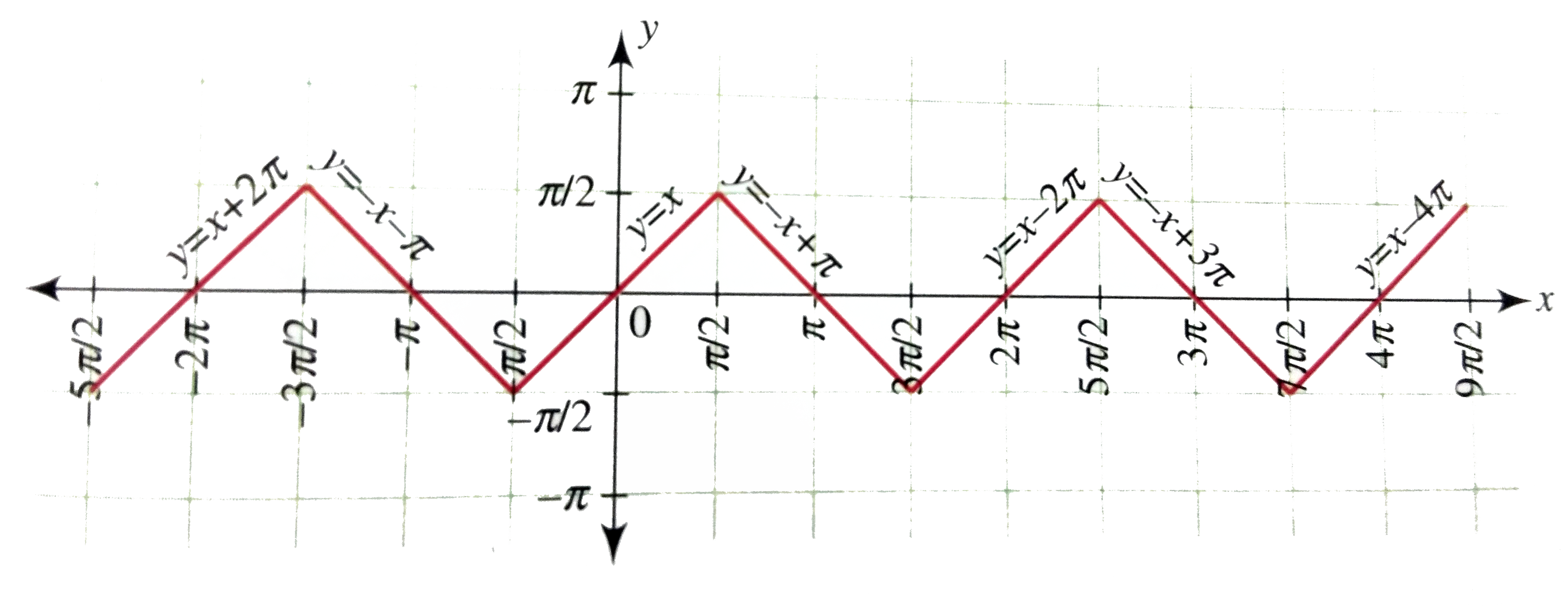
|
|
| 8480. |
Let C be incircle of DeltaABC. If the tangenst of lengths t_(1), t_(2) and t_(3) are drawn inside the given triangle parallel to sides a,b and c, respectively, then (t_(1))/(a )+ (t _(2))/(b)+ (t_(3))/©is equal to |
|
Answer» 0 |
|
| 8481. |
Evalute the following integrals int (sin 2x)/((a + b cos x )^(2))dx |
|
Answer» |
|
| 8482. |
If n_(p_(r)) = 840 , n_(c_(r)) = 35, then n is equal to |
|
Answer» 1 |
|
| 8483. |
A monopolist's demand function is p= 300 - 5x. Find the average revenue function andmarginal revenue function. |
|
Answer» |
|
| 8484. |
Prove that any function f(x) defined in a symmetrical interval (-l, l) can be presented as a sum of an even and an odd function. Rewrite the following functions in the form of a sum of an even and an odd function : (a) f(x)=(x+2)/(1+x^(2))""(b) y=a^x. |
|
Answer» (B) `a^(x)=(a^(x)+a^(-x))/(2)+(a^(x)-a^(-x))/(2)` |
|
| 8485. |
Which of the following forms of haemoglobin is not present in erythrocytes ? |
|
Answer» Methemoglobin |
|
| 8486. |
Evaluate : int (dx)/( (1 - x^(2)) sqrt( 1 + x^(2))) |
|
Answer» |
|
| 8487. |
Let A = ((1,2,3),(0,0,0),(3,2,1)) and A^(n)=((a_(n),b_(n),c_(n)),(0,0,0),(c_(n),b_(n),a_(n))) AA n in N, If a= lim_(nrarroo)(1)/(2^(n-2))(a_(n)+b_(n)+c_(n)) then |a+3i|= ________ |
|
Answer» |
|
| 8488. |
If veca=2hati+3hatj-hatk, vecb= hati+2hatj-5hatk, vec c=3hati+5hatj-hatk, then a vector perpendicular to veca and lies in the plane containing vecb and vec c is : |
|
Answer» `-17hati+21hatj-97hatk` |
|
| 8489. |
Find the eccentricity foci, equation of the directrices and length of the latusrectum of the hyperbola x^(3) - 4y^(2) = 4 |
|
Answer» |
|
| 8490. |
Differentiate the following with respect to x: (1- log x)/(1+ log x) |
|
Answer» |
|
| 8491. |
Find all the values of following . (1 - I sqrt3)^(1//3) |
|
Answer» |
|
| 8492. |
The volume generated by the region bounded by the curve y=sqrt(x) and the line x=0 and x=pi about x axis is : |
|
Answer» `(pi^3)/(3)` |
|
| 8493. |
Compute the integral I _(n) = int_(0)^(1) x^(m) (I n x)^(n) dx , m gt 0,nis a natural number |
|
Answer» |
|
| 8494. |
Verify the Rolle's theorem for each of the function in following questions: f(x)= sin^(4)x + cos^(4)x, "in " x in [0, (pi)/(2)] |
|
Answer» |
|
| 8495. |
Vertices of an isosceles triangle of area a ^(2)are (-a,0) and (a,0). Equation of the circumcircle of the triangle is |
|
Answer» `X ^(2) + y ^(2) + 2ax - 2ay +a ^(2)=0` |
|
| 8496. |
If|x|lt1thenthecoefficientofx ^ 5intheexpansion of(3x ) /((x- 2 ) ( x + 1 ))is |
|
Answer» ` (33 )/(32)` ` = (- 3 ) /(2) x ( 1 +x ) ^(-1 )(1-(x)/(2) ) ^(-1 ) ` `=(-3 ) /(2)x (1- x+x ^ 2-x ^(3 )+x ^ 4.. )(1 +(x ) /(2)+(x ^ 2 ) /(4)+(x ^ 3) /(8)+(x ^ 4 ) /(16 )+... ` `therefore ` COEFFICIENTOF`x ^5` `=( - 3 ) /(2 ) [ (1)/(16) - (1)/(8)+(1 ) /(4) - (1)/(2)+1 ] ` `= (-3)/(2) [(1 - 2+ 4 - 8 +16 )/(16)] ` `= (-3 )/(2) ((11)/(16)) ` `=(-33)/(32)` |
|
| 8497. |
If R is the set of all real numbers and f : R - {2}to R is defined by f(x)=(2+x)/(2-x) for x in R - {2} |
| Answer» ANSWER :D | |
| 8499. |
The value of the expansion (sumsum)_(0 le i lt j le n) (-1)^(i+j-1)"^(n)C_(i)*^(n)C_(j)= |
|
Answer» `"^(2n-1)C_(N)` `sum_(j=0)^(n)sum_(i=0)^(n)(-1)^(i+j-1)'^(n)C_(i)*^(n)C_(j)=sum_(i=0)^(n)(-1)^(2i-1)('^(n)C_(i))^(2)+2S` `:.0=-sum_(i=0)^(n)('^(n)C_(i))^(2)+2S` `:.2S=^(2n)C_(n)` `:.S=^(2n-1)C_(n-1)=^(2n-1)C_(n)` |
|
| 8500. |
The plane 2x-y+3z+5=0 is rotated through 90^(@) about its line of intersection with the plane 5x-4y-2z+1=0. The equation of the plane in the new position is |
|
Answer» `6x-9y-29z-31=0` |
|