Explore topic-wise InterviewSolutions in .

This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.

8401.

The minimum possible distnace between the points A(a, a-1) and B(b, b^(2)+b+1)AA a, b in R is D units, then the value of D^(2) is

Answer»


ANSWER :2
Discussion
8402.

If A=[(3,-2),(4,-2)] and I=[(1,0),(0,1)], find k so that A^(2)=kA-2I

Answer»


ANSWER :k=1
Discussion
8403.

int sin(logx)+cos(logx)dx=

Answer»


ANSWER :`XSIN(LOGX)+C`
Discussion
8404.

ABCDEF is a regular hexagon with centre at the origin such that AD + EB + FC = lambda ED. Then, lambda is equal to

Answer»

2
4
6
3

Solution :Given, AD + EB + FC = `LAMBDA` ED

`implies (AE+ED)+(ED+DB)+2ED=lambdaED`
`implies 4ED+(AE+DB)=lambdaED`
`implies 4ED = lambda ED""[because AE=-DB]`
`implies lambda = 4`
Alternate Method
Now, `AD+EB+FC=2(OD+EO+ED)`
`=2(ED+ED)=4ED`
`therefore lambda = 4`
Discussion
8405.

The solution of the differential equation xy^(2)dy-(x^(3)+y^(3))dx=0 is

Answer»

`y^(3)=3x^(3)+C`
`y^(3)=3x^(3)LOG(cx)`
`y^(3)=3x^(3)+log(cx)`
`y^(3)+3x^(2)=log(cx)`

Answer :B
Discussion
8406.

The value of C(n, 0) - C(n, 1) + C(n, 2) - C(n, 3) +.......+(-1)^(n)C(n, n) =

Answer»

`2^(N)`
0
`1/n`
`2^(n - 1)`

ANSWER :B
Discussion
8407.

If tan.(B-C)/(2)=xcot.(A)/(2), then x =

Answer»

`(C-a)/(c+a)`
`(a-b)/(a+b)`
`(b-c)/(b+c)`
`(b-c)/(a)`

ANSWER :C
Discussion
8408.

Every conditional statement is equivalent to

Answer»

its contrapositive
its inverse
its converse
only itself

Answer :A
Discussion
8409.

int(cosx+sinx)/(sqrt(1+sin2x))dx,x in[-(pi)/(4),(3pi)/(4)]

Answer»


ANSWER :x+c
Discussion
8410.

The pole of the straight line x+4y=4 with respect to the ellipse x^(2)+4y^(2)=4 is

Answer»

(1,1)
(1,4)
(4,1)
(4,4)

ANSWER :A
Discussion
8411.

A is thesetof allprimenumber lessthan10.thennumberof relations in A is

Answer»

14464
28928
65536
115712

Answer :C
Discussion
8412.

Assertion (A) : If 3 + iy is a root of x^(2) + ax + b = 0 then a = -6 Reason (R) : If a, b , c are real and Delta lt 0 the roots of ax^(2) + bx + c = 0 are conjugate complex numbers

Answer»

Both A and R are TRUE R is CORRECT explanation to A
Both A and R are true but R is not correct explanation of A
A is true R is FALSE
A is false R is true

Answer :A
Discussion
8413.

overset((pi)/(2))underset((pi)/(3))int (sqrt(1+cosx))/((1-cos x)^((5)/(2)))dx

Answer»


ANSWER :`(3)/(2)`
Discussion
8414.

Differentiate the following w.r.t. x: (cos x)/(logx), x gt 0, x ne 1

Answer»


ANSWER :`X GT 0`
Discussion
8415.

Find the direction cosine of a line which makes equal angles with the co-ordinate axes.

Answer»


Answer :LET `ALPHA` be the common INCLINATION of the line with the three axes then the d.c.'s of the line are `cosalpha, cosalpha, cosalpha`
If l, m, n are the d.c.'s of a line then `l^2+m^2+n^2=1`
`therefore cos^2alpha+cos^2alpha+cos^2alpha = 1`
`3cos^2alpha = 1`
`cos^2alpha=(1)/3 => cosalpha=pm(1)/sqrt5
Thusm the d.c.'s of line are `pm(1)/SQRT3, pm(1)/sqrt3, pm(1)/sqrt3,`
Discussion
8416.

An aeroplane can carry a maximum of two passengers. A profit of Rs. 1000 is made on each executive clas ticket and a profit of Rs. 600 is made on each economy class ticket. The airline reserves at least 20 seats for executive class. However at least 4 times as many passengers prefer to travel by economy clas than by the executive class. Determine how many tickets of each type must be sold in order to maximise the profit for the airline. What is the maximum profit?

Answer»

Solution :Let `x` passengers are of executive CLASS and `y` passengers are of economy class.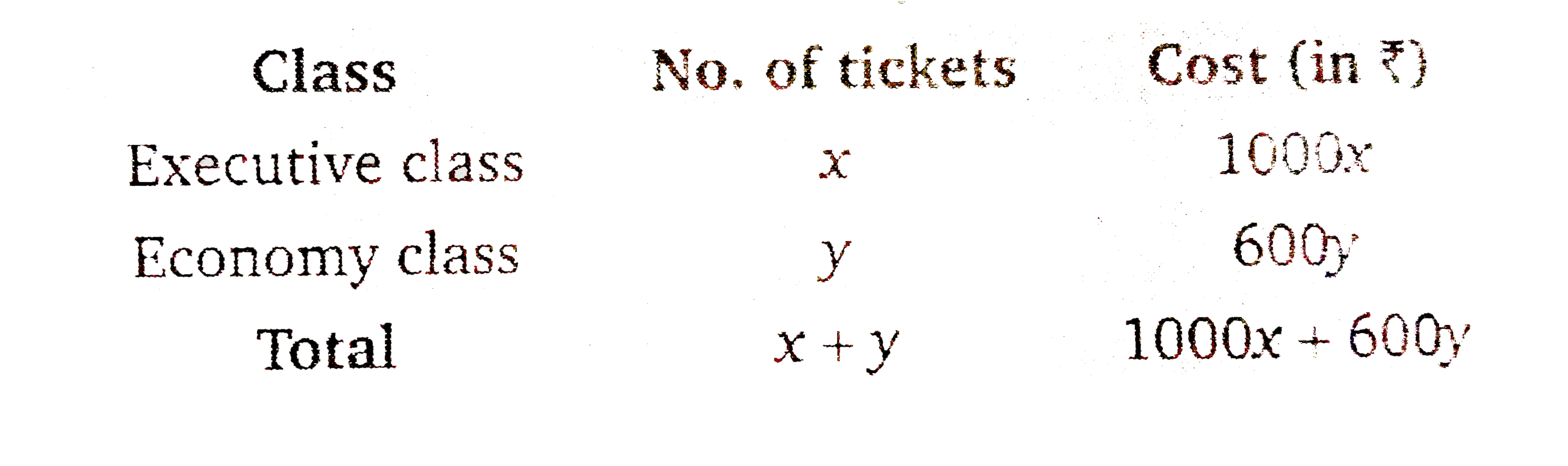

Maximise `Z=1000x+600y`……………1
and constraints `x+yle200`………………2
`xge20`…………….3
`y-4xge0impliesyge4x`…………..4
`xge0,yge0`............5
First draw the graph of the line `x+y=200`.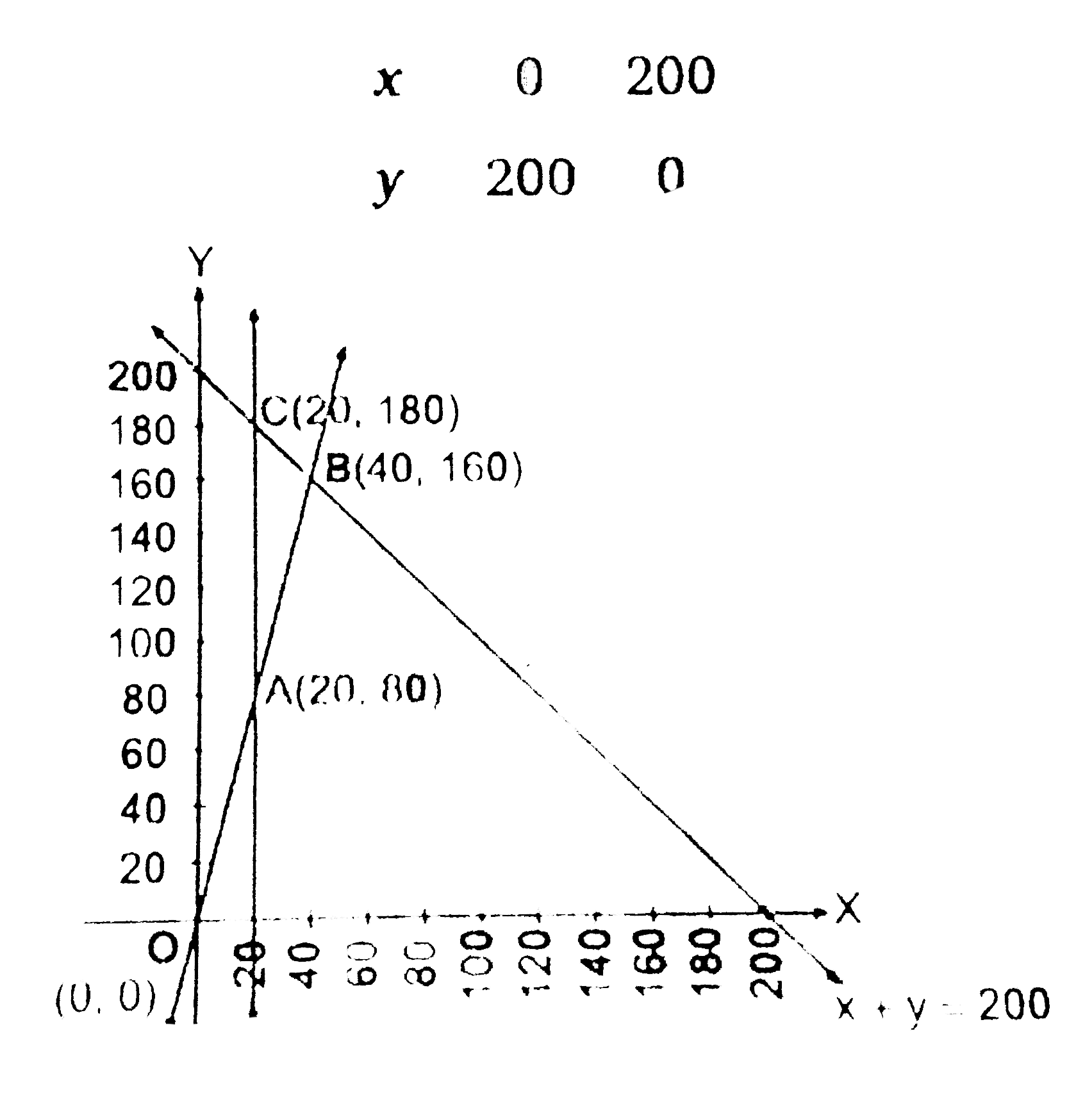

Put `(0,0)` in the INEQUATION `x+yle200`,
`0+0le200implies0le200`. (True)
Thus, half plane contains the origin.
Now, draw the graph of line `y=4x`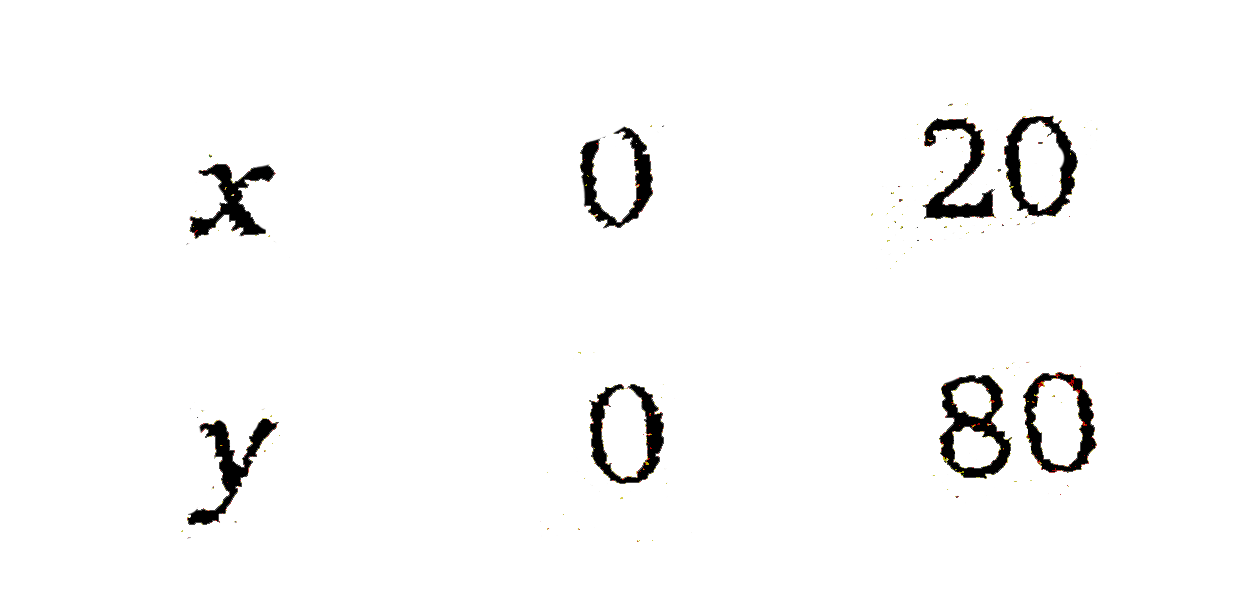

Put `(10,0)` in the inequation `yge4x`,
`0ge4xx10implies0ge40` (FALSE)
Thus, half plane will be opposite to `(10,0)`.
Now draw the graph of line `x=20`
Put `(0,0)` in the inequation `xge0,0ge20` (False)
Thus, the half plane does not contain origin.
Since `x,yge0`, So the feasible region will be in first quadrant.
From the equations the POINTS of intersection are `A(20,80),B(40,160)` and `C(20,180)`.
`:.` Feasible region is ABCA
The vertices of the feasible region are `A(20,80),B(40,160)` and `C(20,180)` at which we find the value of`Z`.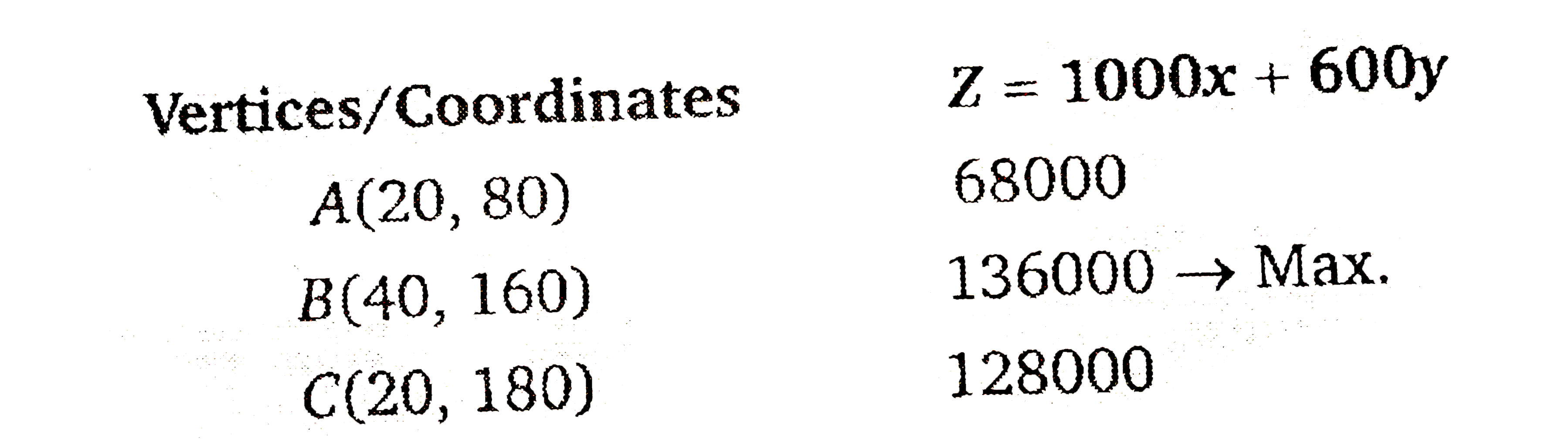

Thus, the maximum value of `Z` is 136000 at point `B(40,160)`. Therefore, maximum cost is Rs. 136000 for which 40 tickets of executive class and 160 tickets of economy class are REQUIRED.
Discussion
8417.

Consider two planes P_(1):2x-3y++z=-5 and P_(2):x-4y-14z=5 if a line L whose points A-=(-7,y_(1),z_(1)) lie on plate P_(1) and points B-=(X_(2),y_(2),z_(2)) and C-=(x_(3),y_(3),z_(3)) lies on plate P_(2) has equation (x+7)/(a)=(y-y_(1))/(-b)=(z-z_(1))/(c) where a,b,c epsilonN and a+b+c is minimum. Q. The minimum value of a+b+c is

Answer»

3
4
5
6

Solution :Line `L:(x+7)/(a)=(y-y_(1))/(-b)=(z-z_(1))/(c)`
`(-7,y,z_(1))` lie on plane `P_(1)`
`implies-3y_(1)+z_(1)=9` ,…(1)
Line L LIES on plate `P_(2)`
`impliesa+4b+14c=0`..(2)
Also `(-7,y_(1),z_(1))` lies on `P_(2)`
`implies-4y_(1)-14z_(1)=12` .. (3)
Form (1) and (3)
Line passes through `(-7,-3,0)`
Least value of a,b,c is `a=2,b=3,c=1`
(from (2))
Discussion
8418.

Consider two planes P_(1):2x-3y++z=-5 and P_(2):x-4y-14z=5 if a line L whose points A-=(-7,y_(1),z_(1)) lie on plate P_(1) and points B-=(X_(2),y_(2),z_(2)) and C-=(x_(3),y_(3),z_(3)) lies on plate P_(2) has equation (x+7)/(a)=(y-y_(1))/(-b)=(z-z_(1))/(c) where a,b,c epsilonN and a+b+c is minimum. Q. The point A is (p,q,r) then p-q+r is

Answer»

<P>3
`-3`
`4`
`-4`

Solution :Line `L:(x+7)/(a)=(y-y_(1))/(-b)=(z-z_(1))/(c)`
`(-7,y,z_(1))` LIE on plane `P_(1)`
`implies-3y_(1)+z_(1)=9` ,…(1)
Line L lies on plate `P_(2)`
`impliesa+4b+14c=0`..(2)
Also `(-7,y_(1),z_(1))` lies on `P_(2)`
`implies-4y_(1)-14z_(1)=12` .. (3)
Form (1) and (3)
Line passes through `(-7,-3,0)`
LEAST value of a,b,c is `a=2,b=3,c=1`
(from (2))
Discussion
8419.

Find the probability of guessing at least 6 out of 10 answers in i) True false type examination ii) Multiple choice with 4 possible answers

Answer»


Answer :i) `UNDERSET(r=6)OVERSET(10)SUM""^(10)C_(r)((1)/(2))^(10)`ii) `underset(r=6)overset(10)sum""^(10)C_(r)((1)/(4))^( r )((3)/(4))^(10-r)`
Discussion
8420.

The slope of a curve at any point on it is the reciprocal of twice the ordinate at that point. If the curve passes through (4,3) then its equation is

Answer»

`y^(2) = x`
`4y^(2) + 9x`
`y^(2) = 2x + 1`
`y^(2) = x + 5`

ANSWER :D
Discussion
8421.

If (veca xx vecb)xx vecc= veca xx (vecb xx vecc) and vecb perpendicular to vecc then which is true ?

Answer»

a)`VECA and vecb` are parallel or `vecc=0`
b)`veca and vecb` are PERPENDICULAR or `vecc=0`
C)`vecc=0`
d)`veca=0`

SOLUTION :N/A
Discussion
8422.

On an average 1 in 100 razor blades manufactured by a firm are defective.If blades are supplied in packets of 5 each, find the probability that a packet has atleast one defective blade. If 1000 packets are tested, in how many packets would you expect defective blades.

Answer»


ANSWER :`1-(0.99)^(5),1000[1-(0.99)^(5)]`
Discussion
8423.

If (1)/(x(x^(2)+a^(2)))=(A)/(x)+(Bx+C)/(x^(2)+a^(2)) then tan^(-1)(A/B)=

Answer»

`(3PI)/(4)`
`pi/4`
`- pi/4`
`pi/3`

ANSWER :C
Discussion
8424.

Consider the sequence in the form of group (1),(2,2)(3,3,3),(4,4,4,4),(5,5,5,5,5…..)

Answer»

1088
1008
1040
none of these

Solution :1,2,2,3,3,3,4,4,4,4,..
LET US write the terms in the groups as follows: 1,(2,2),(3,3,3),(4,4,4,4),… consisting of 1,2,3,4,.. Terms. Let 2000th term fall in nth group. Then,
`((n-1)n)/2lt2000le(n(n+1))/2`
or n(n-1)`lt4000len(n+1)`
Let us consider,
`n(n-1)lt4000`
or `n^(2)-n-4000lt0`
or `nlt(1+sqrt(16001))/2` r `nlt64`
We have
`n(n+1)ge4000` or `n^(2)+n-4000ge0` or `nge63`
That means 2000th term falls in 63RD group, which means that the 2000th term is 63. Now, the TOTAL number of terms up to 62nd group is `(62xx63)//2=1953`. Hence, the sum of first 2000 terms is
`1^(2)+2^(2)+..+62^(2)+63(2000-1953)`
`=(62(63)125)/6+63xx47=84336`
Sum of the remaining terms=`63xx16=1008`.
Discussion
8425.

If x=9 is a chord of contact of the hyperbola x^(2)-y^(2)=9, then the equation of the tangent at one of the points of contact is

Answer»

`x+sqrt3y+2=0`
`3x-2sqrt2y-3=0`
`3x-sqrt2y+6=0`
`x-sqrt3y+2=0`

ANSWER :B
Discussion
8426.

A general insurance company insuring vehicles for a period of one year classifies its policy holders into three mutually exclusive group. Group T_(1) : Policy holders with very high risk factor Group T_(2): Policy holders with high risk factor Group T_(3) : Policy holders with less risk factor From the past experience of the company, 30% of its policy holders belong to group T_(1), 50% belong to group T_(2), & the rest belong to group T_(3). If the probabilities that policy holders belonging to groups T_(1),T_(2) and T_(3) meet with an accident are 0.30, 0.15 and 0.05 respectively, find the proportion of policy holders having a policy for one year will meet with an accident. If a randomly selected policy holder does not meet with an accident, what is the probability that he belongs to group T_(2) ?

Answer»


ANSWER :`(17)/(33)`
Discussion
8427.

If (1/3)^x=(81)^(x-1), find the value of x .

Answer»


ANSWER :D
Discussion
8428.

If sum _( r -1) ^(n) T_(r) = (n (n +1)(n+2))/(3), then lim _(x to oo) sum _(r =1) ^(n) (3012)/(T_(r))=

Answer»

2008
3012
4016
8032

Answer :A
Discussion
8429.

{ x in R:(14x)/(x+1)-(9x-30)/(x-4)lt0} is equal to

Answer»

`(-1,4)`
`(1,4)CUP (5,7)`
`(1,7)`
`(-1,1) cup(4,6)`

ANSWER :D
Discussion
8430.

If the light source in front of an eye becomes bright suddenly :-

Answer»

FOCUS of LENS will change
Retina is BLEACHED
Vitreous HUMOR is decondensed
Pupil will constrict

Answer :A
Discussion
8431.

How many enzymes are active in given enzymes ? Trypsin, Chymotrypsinogen, Pro carboxypeptidase, Pepsinogen, Rennin

Answer»

1
2
3
4

Answer :A
Discussion
8432.

Find the coordinates of the vertex and focus, the equation of the directrix and axis of the following parabolas. (ii) x^(2) - 2x + 4y -3=0

Answer»


ANSWER :VERTEX `(1,1)`, Focus `(1,)`, DIRECTRIX `y=2`, AXIS `x=1`
Discussion
8433.

Find the coordinates of the vertex and focus, the equation of the directrix and axis of the following parabolas. (i) y^(2) + 4x + 4y-3

Answer»


Answer :Vertex `( (7)/(2) ,-2)`, Focus `((3)/(4) , -2)`, DIRECTRIX `4x-11=0`, AXIS `y+2=0`
Discussion
8434.

If A,B and C are mutually exclusive and exhaustive events such that P(B)=(3)/(2)P(A) and P(C )=(1)/(3)P(B). Find odds in favour of (AuuB)

Answer»


ANSWER :`5 : 1`
Discussion
8435.

Which of the followintg is true if A+B+C = pi

Answer»

`sin 2A + SIN2B + sin 2C = 4 sinA sinB SINC`
`sinA + sinB + sinC = 4 cos'A/2 cos 'B/2 cos'C/2`
`cos 2A + cos 2B + cos 2C = - 1- 4 cos A cos B cos C`
`cos A + cos B + cos C = 1 + 4 sin 'A/2 sin 'B/2 sin 'C/2`

Answer :A
Discussion
8436.

Find the value of(627)^(1//4)correct to 4 decimals places

Answer»


ANSWER :`5.004 `
Discussion
8437.

Annual Budgets for Different Programs in Kansas, 2007 to 2010 The table above lists the annual budget, in thousands of dollars, for each of six different state programs in Kansas from 2007 to 2010. Which of the following best approximates the average rate of change in the annual budget for agriculture/natural resources in Kansas from 2008 to 2010 ?

Answer»

`$50,000,000` PER YEAR
`$65,000,000` per year
`$75,000,000` per year
`$130,000,000` per year

Answer :B
Discussion
8438.

Which of the following functions have the same period ?

Answer»

`f(x)=SIN^(2)(x) +COS^(4)x+2`
`g(x)=(1)/(f(sin x))+(1)/(f(cos x))` where `f(x)=(1)/(sqrt(1-x^(2)))`
`h(x)=(|sin x|+|cos x|)/(|sinx-cosx|)`
`k(x)=cos(cos x)+cos(sin x)`

SOLUTION :ABD
A,B,D each have a period `pi//2`, and C has a period `pi`
Discussion
8439.

If f(x) =[ sin ^(-1)(sin 2x )] (where, [] denotes the greatest integer function ), then

Answer»

`int_(0)^(pi//2) F(x) dx=(pi)/(2) - sin ^(-1)(sin 1)`
`f(x)` is periodic with period `pi`
`underset(x rarr(pi)/(2))(lim) f(x)=-1`
NONE of thses

Answer :A::B::C
Discussion
8440.

If A is a 2xx2 non singular matrix, then adj(adj A) is equal to :

Answer»

`A^(2)`
A
`A^(-1)`
`(A^(-1))^(2)`

ANSWER :B
Discussion
8441.

Parameters of binomial distribution of variable X are 2n +1and p =(1)/(2). Then …….. Is the probability that random variable X takes odd numbers.

Answer»

`(1)/(2)`
`(1)/(2^(N))`
`(1)/(2^(n+1))`
`(3)/(2)`

ANSWER :A
Discussion
8442.

Form the differential equation of the family of parabolas having vertex at origin and axis along positive y-axis.

Answer»


ANSWER :`2XYY' + X^(2) = y^(2)`
Discussion
8443.

The value ofcot16^(@) cot44^(@) + cot44^(@) cot76^(@)- cot76^(@) cot16^(@) is…………….

Answer»


ANSWER :3
Discussion
8444.

Evaluate int((e^(x) )/(e^(2x) + 4e^(x) + 10))dx

Answer»
Discussion
8445.

Using the properties of determinants in Exercise 1 to 6, evaluate |{:(a-b-c,2a,2a),(2b,b-c-a,2b),(2c,2c,c-a-b):}|

Answer»


ANSWER :`thereforeD=(a+b+c)^3`
Discussion
8446.

The proposition (p rarr ~p) ^^ (~p rarr p) is

Answer»

a TAUTOLOGY
a contradiction
neither a tautology nor a contradiction
a tautology and a contradiction

Answer :B
Discussion
8447.

Determine lambda such that a vector vec(r) is at right angles to each of the vectors vec(a) = lambda hat(i) + hat(j) + 3hat(k), vec(b) = 2hat(i) + hat(j) - lambda hat(k), vec(c) = -2hat(i) + lambda hat(j) + 3hat(k).

Answer»


ANSWER :`LAMBDA = 0`
Discussion
8448.

Prove theat the Drichlet function lambda(x) is a periodic one but has not period.

Answer»


ANSWER :`lambda(X+r)=lambda(x)={{:(,"1 for RATIONAL x"),(,"0 for irrational x"):}`.
Discussion
8449.

Transform the equation 4x + 3y - 12 = 0 into intercept form.

Answer»


ANSWER :`(X)/(-3)+(y)/(4)=1`
Discussion
8450.

Let A = { a,b,c }, absB = {1,2} Determine all the relations from A to B and determine the domain range and inverse of each relation.

Answer»

Solution :A = {a,B,c} , B = {1,2]
`THEREFORE A xx B` = {(a,1), (a,2), (b,1),(b,2),(c,1),(c,2)}
`therefore ABS(A xx B)` = 6
`therefore ABSP(A xx B ) = 2^6 = 64
Discussion