Explore topic-wise InterviewSolutions in .

This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.

8501.

If c is a parameter, then the differential equation whose solution is y=c^(2)+(c )/(x), is

Answer»

`y=((DY)/(DX))^(2)-(d^(2)y)/(dx^(2))`
`y^(4)((dy)/(dx))^(2)-x(dy)/(dx)`
`y=((dy)/(dx))^(2)-x(dy)/(dx)`
`y=x(dy)/(dx)-2x^(2)(d^(2)y)/(dx^(2))`

ANSWER :B
Discussion
8502.

Match List I with List II and select the correct answer using the codes given below the lists :

Answer»

`{:(a,b,c,d),(s,r,p,q):}`
`{:(a,b,c,d),(q,s,r,p):}`
`{:(a,b,c,d),(s,r,p,q):}`
`{:(a,b,c,d),(q,s,p,r):}`

Solution :`tan^(-1) ((1)/(2x + 1)) + tan^(-1) ((1)/(4X + 1)) = tan^(-1).(2)/(x^(2))`
`rArr tan^(-1) ((3X + 1)/(4x^(2) + 3x)) = tan^(-1).(2)/(x^(2))`
`rArr 3x^(2) - 7x -6 = 0`
`rArr x = -(2)/(3) , 3`
But for `x -(2)/(3)`, L.H.S is negative and R.H.S. is positive
Hence, the only solution is `x = 3`
NOTE : Solution of the remaining parts are given in their respective chapters
Discussion
8503.

Two fair dice are rolled. Find the probability that the difference between the numbers is atleast 2.

Answer»


ANSWER :`(5)/(9)`
Discussion
8504.

A Die marked 1, 2, 3 in red and4. 5, 6 in green is tossed. Let A be the event, 'number is even's and B be the event, 'number is red'. Are A and B independent ?

Answer»


ANSWER :A and B are not INDEPENDENT
Discussion
8505.

Match the following for the system of linear equations If A is non-singular matrix of order nxxn then(##FIITJEE_MAT_MB_07_C02_E04_002_Q01.png" width="80%">

Answer»


ANSWER :A::B::C::D
Discussion
8506.

There are two ums. Um A has 3 distinct red balls and um B has 9 distinct blue balls. From each um two balls are taken out at random and them transferred to the other . The number of ways in which this can be done is

Answer»

36
66
108
3

Answer :C
Discussion
8507.

A company manufacturers two types of products P and Q. The product P requires 5 minutes each for cutting and 10 minutes each for assembling. The product Q requires 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours 20 minutes availabe for cutting and 4 hours for assembling. The profit is 50 paise each for type P and 60 paise each for type Q. How many products of each type should the company manufacture inorder to maximize the profit?

Answer»


SOLUTION :NA
Discussion
8508.

C(15,12)=

Answer»
Discussion
8509.

If |{:(1,2,5),(1,x,5),(3,-1,2):}|=0 then x = ………

Answer»

2
-2
5
-5

Answer :A
Discussion
8510.

Let f(x)={(-2,-3 lex le0),(x-2,0 lt x le3):}, where g(x) = min {f(|x|)+|f(x)|, f(|x|)-|f(x)|}. Find the area bounded by the curve g(x) and the X-axis between the ordinates at x=3 and x=-3.

Answer»


ANSWER :`23/2` SQ UNITS
Discussion
8511.

If therootsof24x^3 - 26 x^2+ 9x -1=0 areinH.Pthentherootsare

Answer»

`1/2,1/3,1/4`
`1,1/3,1/8`
`1/8,1/3,1/3`
`2,3,4`

ANSWER :A
Discussion
8512.

For any two statements p and q, ~(pvvq)vv(~p^^q) is logically equivalents to

Answer»

<P>p
`~p`
Q
`~q`

ANSWER :B
Discussion
8513.

A rectangular metal ................

Answer»


Solution :The COEFFICIENT of VISCOSITY is the ratio of tangential stress on top surface of film (exerted by block) to that of velocity gradient (vertically downwards) of film. Since mass m moves with constant velocity, the string exerts a force EQUAL to mg on plate towards right. Hence oil shall exert tangential force mg on plate towards left.
`:. eta=(F//A)/((v-0)//Delta x)=(125xx1000//10xx20)/((5-0)//.02)=2.5` DYNE - `s//cm^(2)`
Discussion
8514.

Find the derivative of x=log(1+sqrty) w.r. to x.

Answer»


ANSWER :B
Discussion
8515.

int((2x-1)^(2)(x+3))/(sqrt(x))dx

Answer»


ANSWER :`(8)/(7)X^(7//2)+(16)/(5)x^(5//2)-(22)/(3)x^(3//2)+6x^(1//2)+C`
Discussion
8516.

Construct truth tables for the following and indicate which of these are tautologies (p rarr q) rarr[(q rarrr)rarr(p rarr r)]

Answer»

SOLUTION :
Discussion
8517.

Show that the points (1,2,3), (2,3,1) and (3,1,2) from an equilateral triangle.

Answer»
Discussion
8518.

Calculate whenever possible,[[2],[3]][[1,2],[4,3]]

Answer»

Solution :`[[2],[3]][[1,2],[4,3]]` is impossibel because number of COLUMNS of 1st `!=` number of rows of SECOND.
Discussion
8519.

What can you say about the set, A,B,ifA nn B =U.(where U is the universal set)

Answer»

SOLUTION :`ANN B =U IMPLIES A=B=U`
Discussion
8520.

If (x^(2)+1)/((x^(2)+2)(x^(2)+3))=(A)/(x^(2)+3)+(B)/(x^(2)+2) then (A, B)=

Answer»

(1, 2)
(2, -1)
(1, -2)
(-2, -1)

ANSWER :B
Discussion
8521.

Let the equation of a straight line L in complex form be abarz+baraz+b=0, where is a complex number and b is a real number then

Answer»

the straight line `(z-c)/a +(i(barz-barc))/a=0` makes a angle of `45^(@)` with `L` and passed through a point `c` (where `c` is a complex number)
the straight line `(z-c)/a=(i(barz-barc))/(bara)` makes an angle of `45^(@)` with `L` and passes through `a` and `c` (where `c` is a complex number)
the complex slope of the line `L` is `-a/a`
the complex slope of the line `L` is `a/a`

Solution :Let `P(z)` be any pointon the required line.
Then, `(vec(CP))/(|vecCP|)` i.e. `(z-c)/(|z-c|)` is a unit vector parallel to it
Let `A(z_(1))` and `B(z_(2))` be TWO points on
`baraz+abarz+b=0` then `(z_(2)-z_(1))/(|z_(2)-z_(1)|)` is a unit vector parallel to the line
`abarz+baraz+b=0`
`(z-c)/(|z-c|)=(z_(2)-z_(1))/(|z_(2)-z_(1)|)e^(+-i((pi)/4))`
`((z-c)^(2))/((z-c)(barz-barc))=((z_(2)-z_(1))^(2))/((z_(2)-z_(1))(barz_(2)-barz_(1)))e^(+-i(pi)/2)`
`((z-c)/(barz-barc))= +- i ((z_(2)-z_(1))/(barz_(2)-barz_(1)))`.......(1)
`:' A(z_(1)` and `B(z_(2))` are on the line `abarz+baraz+b=0`therefore `abarz_(1)+baraz_(1)+b=0`
`abarz_(2)+baraz+b=0`
`implies-a/a=(z_(2))/(barz_(2))=((z_(2)-z_(1))/(barz_(2)-barz_(1)))`......(2)
From EQUATION (1) and (2) we get `(z-c)/a+-(i(barz-barc))/(bara)=0`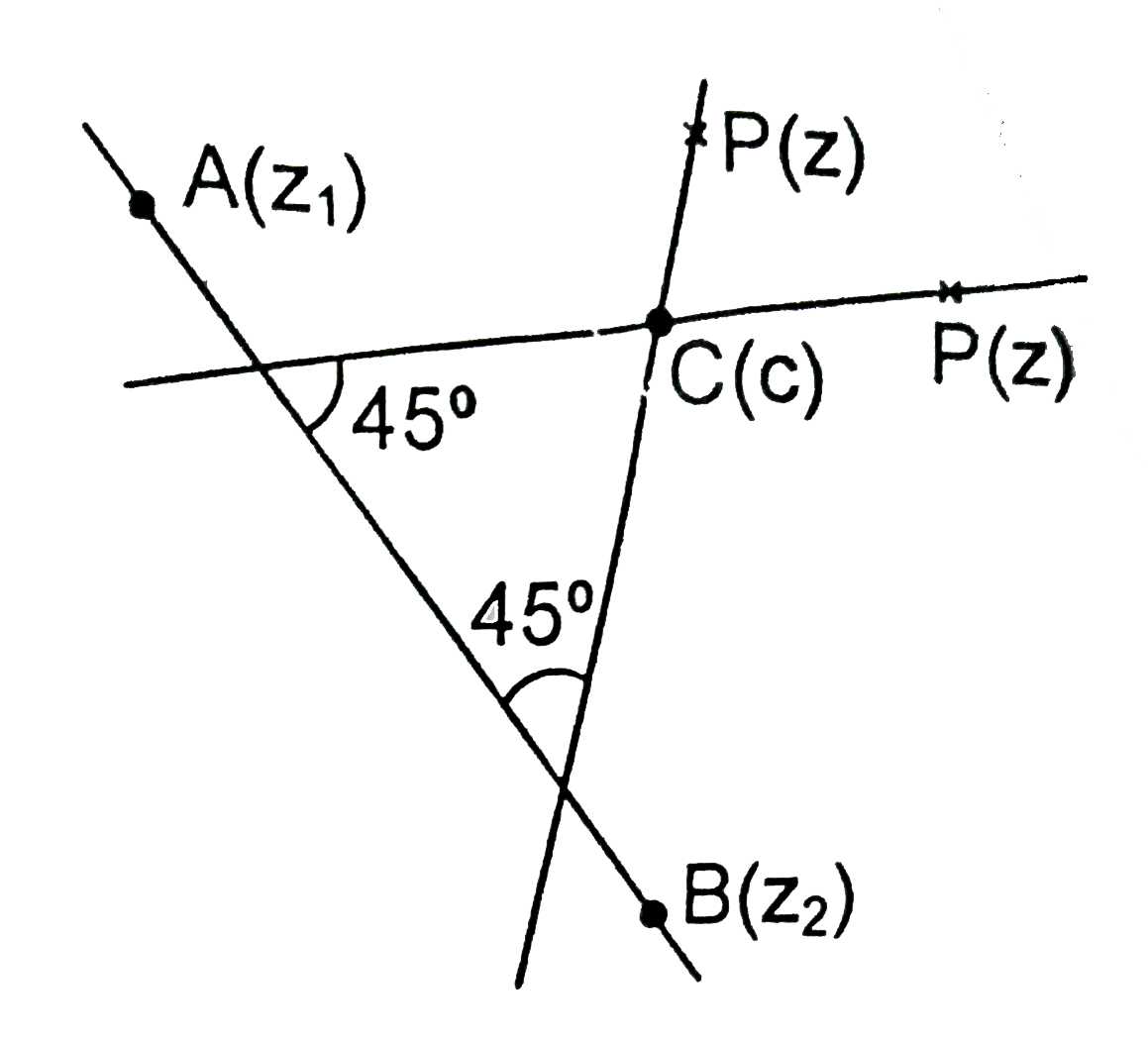
Discussion
8522.

Solve x^4-4x^2+8x+35=0 Given (2+isqrt3) is a root.

Answer»


ANSWER :`-2pmi`
Discussion
8523.

Read the following writeup carefully: A, B, C are the points representing the complex numbers z_1, z_2 and z_3 respectively (such that no-two are equal)on the complex place and |z_1| =|z_2|=|z_3| Now answer the following question If the altitude at the vertex A of Delta ABC meets the circumcircle again at P, then complex number representing point P is

Answer»

`-(z_2 z_3)/(z_1)`
`-(z_1 z_2)/(z_3)`
`-(z_1 z_3)/(z_2)`
`-((z_2 + z_3))/(z_1)`

ANSWER :A
Discussion
8524.

Which of the given values of x and y make the following pair of matrices equal : [(3x+7,5),(y+1,2-3x)],[(0,y-2),(8,4)]

Answer»

`x=-1/3,y=7`
Not POSSIBLE to FIND
`y=7,x=-2/3`
`x=-1/3,y=-2/3`.

ANSWER :B
Discussion
8525.

Read the following writeup carefully: A, B, C are the points representing the complex numbers z_1, z_2 and z_3 respectively (such that no-two are equal)on the complex place and |z_1| =|z_2|=|z_3| Now answer the following question The focus of a point Q (z) which touches the circumcircle of Delta ABC and the line z+ bar(z) -2 =0 (given that |z_1| = |z_2| = |z_3|=1 ) is

Answer»

`(z - bar(z))= 4(z + bar(z) )^2`
`(z - bar(z))^2 + 4 (z + bar(z))=0`
ARG `(z) = 2n pi , n in I`
Arg `(z-1)= 2 n pi, n in I`

ANSWER :D
Discussion
8526.

Statement -1 : sin 3 le sin 1 le sin2 Statement-2 : sinxis positive in the first and second quadrants .

Answer»

Statement-1 is TRUE, Statement-2 is True and Statement-2 is a CORRECT EXPLANATION for Statement-1.
Statement-1 is True, Statement-2 is True and Statement-2 is NOT a correct explanation forStatement-1.
Statement-1 is True, Statement-2 is FALSE
Statement-1 is False, Statement-2 is True

Answer :B
Discussion
8527.

Show that S_(n)=(n(2n^(2)+9n+13))/(24).

Answer»

Solution :Let `T_(N)` and `T_(n)'` be the nth terms of the series in numerator and denominaror of LHS. Then,
`THEREFORE T_(n)=n(n+1)^(2)" and " T_(n)'=n^(2)(n+1)`
`therefore LHS=(sumT_(n))/(sumT_(n))=(sumn(n+1)^(2))/(sumn^(2)(n+1))=(sum(n^(3)+2N^(2)+n))/(sum(n^(3)+n^(2)))`
`=(sumn^(3)+2sumn^(2)+sumn)/(sumn^(3)+sumn^(2))`
`=({n(n+1)/(2)}^(2)+2{n(n+1)(2n+1)/(6)}+{n(n+1)/(2)})/({n(n+1)/(2)}^(2)+{(n(+1)(2n+1))/(6)})`
`=((n(n+1))/(2){(n(n+1))/(2)+(2(2n+1))/(3)+1})/((n(n+1))/(2){(n(n+1))/(2)+(2n+1)/(3)})`
`=((1)/(6)(3n^(2)+3n+8n+4+6))/((1)/(6)(3n^(2)+3n+4n+2))`
`=((3n^(2)+11n+10))/((3n^(2)+7n+2))=((3n+5)(n+2))/((3n+1)(n+2))=((3n+5))/((3n+1))=RHS`.
Discussion
8528.

If m and n are positive integers and f(m,n)=int_(0)^(1)x^(n-1)(logx)^(m)dx, then f(m,n) is equal to

Answer»

`m/nf(m-1,N)`
`-m/nf(m-1,n)`
`n/mf(m-1,n)`
NONE of these

Answer :B
Discussion
8529.

If A is 3 xx 3 square matrix whose characteristics polynomical equations is lambda^(2)-2lambda^(2)+4=0 then trace of adj A is

Answer»

0
3
4
`-3`

ANSWER :A
Discussion
8530.

Consider the line 3x – 4y + 2 = 0 and the point (2, -3) Find the distance of the point from the line.

Answer»


ANSWER :i. 4, ii. `((-14)/(5), (17)/(5))`
Discussion
8531.

Number of values of 'x' satisfying |x+1|-|x|+|x-3|=4 is :-

Answer»

1
2
3
4
Discussion
8532.

Find the area of the region bounded between the parabola x^(2)=y and the curve y=|x|.

Answer»


ANSWER :`1/3`
Discussion
8533.

If uis a constant and v is a variable then(du)u^v In v/(dv)=__________.

Answer»

`u^v` In v
`VU^(v-1)`
`u^v` In u
`UV^(v-1)`

ANSWER :C
Discussion
8534.

Evaluate the integrals. int [ (2x - 1)/(3 sqrt(x)) ]^(2) " dx , " (x gt 0 )

Answer»


ANSWER :`(4)/(18) x^(2) - (4)/(9)x +(1)/(9) log |x|` + c
Discussion
8535.

Form the differential equation by eliminating the arbitrary constant from the equation y = e^(3x) (a cos x + b sin x)

Answer»

`(d^(2)y)/(DX^(2)) - 6 (DY)/(dx) - 10Y = 0`
`(d^(2)y)/(dx^(2)) -6 (dy)/(dx) + 10y = 0`
`(d^(2)y)/(dx^(2)) + 6 (dy)/(dx) + 10y = 0`
`(d^(2)y)/(dx^(2)) -6 (dy)/(dx) + 6y = 0`

Answer :B
Discussion
8536.

The shortest distance between the lines x+a=2y=-12z and x=y+2a=6z-6a is

Answer»

a
2a
4a
6a

Answer :B
Discussion
8537.

Find the value of [a] if the lines (x-2)/(3)=(y+4)/(2)=(z-1)/(5) & (x+1)/(-2)=(y-1)/(3)=(z-a)/(4)are coplanar (where [] denotes greatest integer function)

Answer»


SOLUTION :`|(3,-5,1-a),(3,2,5),(-2,3,4)|=0 rArr a=(102)/(13)`
Discussion
8538.

Find the number of ways of arranging the letters of the word SPECIFIC. In how many of them the two I's do not come together

Answer»


ANSWER :2520
Discussion
8539.

Find the approximate value of (1.999)^(5).

Answer»


ANSWER :`31.920`
Discussion
8540.

A box contains 2 gold and 3 silver coins. Another box contains 3 gold and 3 silver coins. A box is chosen at random, and a coin is drawn from it. If the selected coin is a gold coin, find the probability that it was drawn from the second box.

Answer»


ANSWER :`5/9`
Discussion
8541.

int_(0)^(a)sqrt((a+x)/(a-x))dx=

Answer»


ANSWER :`a((PI + 2)/(2))`
Discussion
8542.

A pair of dice is thrown. Find the probability that the sum is 10 or greater if 5 appears on atleast one of the dice.

Answer»


ANSWER :`(3)/(11)`
Discussion
8543.

Consider the two circles C_(1):x^(2)+y^(2)=a^(2)andC_(2):x^(2)+y^(2)=b^(2)(agtb) Let A be a fixed point on the circle C_(1), say A(a,0) and B be a variable point on the circle C_(2). The line BA meets the circle C_(2) again at C. 'O' being the origin. The locus of the mid-point of AB is

Answer»

`(X-(a)/(2))^(2)+y^(2)=(B^(2))/(4)`
`(x-(a)/(2))^(2)+y^(2)=(a^(2))/(4)`
`(x-(b)/(2))^(2)+y^(2)=(a^(2))/(4)`
`(x-(b)/(2))^(2)+y^(2)=(b^(2))/(4)`

ANSWER :A
Discussion
8544.

If |{:(cos (A+B), -sin (A+B), cos 2B),(sin A, cos A, sin B), ( -cos A, sin A, cos B):}|=0, then B is equal to

Answer»

`(2N +1) PI/2`
`(2n +1)pi`
`NPI`
`2n pi`

ANSWER :A
Discussion
8545.

Find the area of the region enclosed by the curves y=x^(2)-4x+3 and the x-axis

Answer»


ANSWER :`(4)/(3)`
Discussion
8546.

Prove that the equation of the chord joining the points alpha and beta on the ellipse x^2/a^2+y^2/b^2=1 is

Answer»


ANSWER :`COS "(ALPHA BETA)/2`
Discussion
8547.

Complex numbers z_1,z_2,z_3 are the vertices A,B,C respectively of an isosceles right angled triagle with (z_1-z_2)^2=(z_1-z_3)(z_3-z_2)

Answer»

Solution :SINCE , triangle is a RIGHT angled ISOSCELES triangle
`therefore` Rotating `z_(2)` about `z_(3)` in anti-clockwise direction through an angle of `pi//2` , we get
`(z_(2) - z_(3))/(z_(1) - z_(3)) = (|z_(2) - z_(3)|)/(|z_(1) - z_(3)|)e^((pi//2))`
where , `|z_(2) = z_(3)| = |z_(1) - z_(3)|`
`implies (z_(2) - z_(3))^(2) = -(z_(1) - z_(3))^(2)`
`implies z_(2)^(2) + z_(3)^(2) - 2z_(2)z_(3) = - z_(1)^(2) - z_(3)^(2) + 2z_(1)z_(3)`
`implies z_(1)^(2) + z_(2)^(2) - 2z_(1)z_(2) = 2z_(1)z_(3) + 2z_(2) z_(3) - 2 z_(3)^(2) - 2z_(1) z_(2)`
`implies (z_(1) - z_(2))^(2) = 2{(2z_(1) z_(3)^(2)) + (z_(2)z_(3) - z_(1)z_(2))}`
`implies (z_(1) - z_(2))^(2) = 2(z_(1) - z_(3)) (z_(3) - z_(2))`
Discussion
8548.

Find the value of sum_(k=1)^(10){sin((2kpi)/(11))-i cos ((2kpi)/(11))}

Answer»


ANSWER :i
Discussion
8549.

Arrange the following according to their values in ascending order A) int_(0)^(pi) |sin x| dx B) int_(0)^(2pi) |sin x | dx C) int_(0)^(3pi) |sin x| dx

Answer»

A, B, C
C, B, A
C, A, B
A, C, B

Answer :A
Discussion
8550.

Let f(x) be a twice differentiable function in (-oo, oo) such that f''(x)lt 0 AA x in R, g(x)=f(x)+f(1-x) and g'((1)/(4))=0 then

Answer»

g(x) is increasing in `(-oo, (1)/(4))`
g(x) attains local minima at `x=(1)/(2)`
minimum number of zeroes F `g''(x)` is 2 in [0, 1]
`g'(x) lt 0 " in "((1)/(2), oo)`

Answer :A,C,D
Discussion