Explore topic-wise InterviewSolutions in .

This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.

8651.

Evaluate: int_(0)^((pi)/(2))(xsinxcosxdx)/(cos^(4)x+sin^(4)x)

Answer»


ANSWER :`(PI^(2))/(16)`
Discussion
8652.

If the 2^(nd) and 5^(th) terms of G.P. are 24 and 3 respectively then the sum of 1^(st) six terms is :

Answer»

`(2)/(189)`
`(179)/(2)`
`(189)/(5)`
`(189)/(2)`

ANSWER :D
Discussion
8653.

From centre O, of the ellipse (x^2)/(16)+(y^2)/(9)=1, two perpendicular rays are drawn meeting the ellipse at P and Q, N is the foot of perpendicular from O to PQ, then:

Answer»

`(1)/(OP^2)+(1)/(OQ^2)=(25)/(144)`
`(1)/(OP^2)-(1)/(OQ^2)=(25)/(144)`
`ON=(12)/(5)`
`ON=(6)/(5)`

ANSWER :A::C
Discussion
8654.

What is differential of y?

Answer»


ANSWER :dy=f'(X)DX
Discussion
8655.

Find the remainder when (sum_(r=1)^(5)""^(20)C_(2r-1))^(6) is divided by 11.

Answer»


Solution :We have `E = (underset(r=1)overset(5)sum.^(20)C_(2r-1))^(6)`
We know that `.^(20)C_(1)+.^(20)C_(3)+.^(20)C_(5)+.^(20)C_(7)+"......"+.^(20)C_(19)=2^(19)`
Now, `.^(20)C_(1)=.^(20)C_(19),.^(20)C_(3)=.^(20)C_(17)"....."`ETC.
`:. 2(.^(20)C_(1)+.^(20)C_(3)+"...."+.^(20)C_(9))=2^(19)`
`rArr .^(20)C_(1)+.^(20)C_(3)+"....."+.^(20)C_(9)=2^(18)`
`rArr E = (2^(18))^(6) = 2^(108)`
`= 8(2^(5))^(21)`
`= 8(33-1)^(21)`
`= 8(33k-1)`
`= 8 xx 33k - 8`
`= 11(8xx3k-1)+3`
Therefore, the REMAINDER when `(underset(r=1)overset(5)sum.^(20)C_(2r-1))^(6)` is divided by 11 is 3.
Discussion
8656.

int (sin x - cos x )/(sqrt(sin 2x))dx =

Answer»

`- "COSH"^(-1) ` (SIN x + COS x)+ c
`"cosh"^(-1) ` (sin x + cos x ) + c
`-"sinh"^(-1) ` (sin x + cos x ) + c
`"sinh"^(-1)` (sin x + cos x ) + c

ANSWER :A
Discussion
8657.

Examine the consistency of the following system of equation 2x-y =5 x+y=4

Answer»

SOLUTION :`|A| =3 !=0`
`rArr`A is non-singular.
`therefore`The GIVEN SYSTEM is consistent.
Discussion
8658.

Determine the area bounded by the rectangular hyperbola xy=c^(2) ,the x -axis and the two ordinates x =c,x=2c

Answer»


ANSWER :`C^(2) LOG2` square UNITS
Discussion
8659.

Consider f(x){{:(|[x]|",",0le{x}lt(1)/(2),,),(,,,","AAx in[(-7)/(2),(7)/(2)]),(|x|",",(1)/(2)le{x}lt1,,):} Number of solution of the equation f(x)=(5)/(2) is equal to

Answer»

2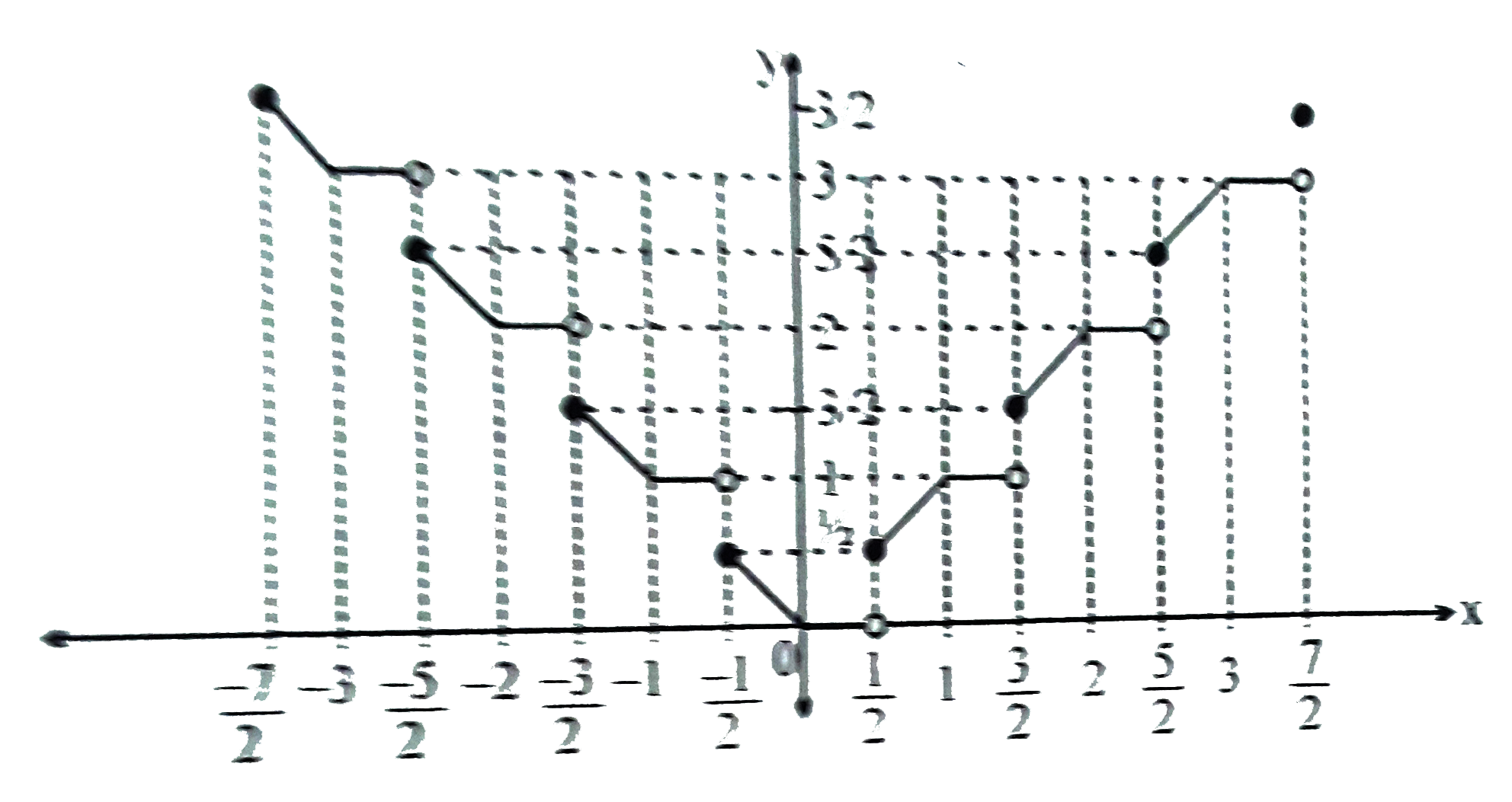
3
4
infinite

Solution :
L = Number of POINT of DISCONTINUOUS = 7
M = Number of point non-differentiability = 14
HENCE (L+M)=21.
Discussion
8660.

Find the angle between the planes whose vector equations are vecr.(2hati+2hatj-3hatk)=5 andvecr.(3hati-3hatj+5hatk)=3.

Answer»


Answer :`THEREFORE theta=cos^(-1)((15)/(SQRT(731))`
Discussion
8661.

Evaluate: intsqrt(("cosec"x-cotx)/("cosec"x+cotx).(secx)/sqrt(1+2secx)dx

Answer»

SOLUTION :`SIN^(-1)(1/2sec^(2)x/2)+C`
Discussion
8662.

The sum of (n+1) terms of the series (C_0)/(2)-(C_1)/(3)+(C_2)/(4)-(C_3)/(5)+…. is

Answer»

`(1)/(N+1)`
`(1)/(n+2)`
`(1)/(n(n+1))`
`(1)/((n+1)(n+2))`

ANSWER :D
Discussion
8663.

Let f(x) ={{:(x(x-1)(x-2),(0lexltn),sin(pix),(nlexle2n):} least value of n for which f(x) has more points of minima than maxima in [0,2n] is _____.

Answer»


SOLUTION :(1) for n =1graph of F(X)

(2) for n=2 graph of f(x)

for n=3 graph of f(X)
Discussion
8664.

The probability of India winning a test match against West-Indies is 1//2 assuming independence from match to match. The probability that in a match series India's second win occurs at the third test is

Answer»

`(1)/(8)`
`(1)/(4)`
`(1)/(2)`
`(2)/(3)`

ANSWER :B
Discussion
8665.

A = {8^(n) - 7n - 1 : n in N}, B = {49(n-1) : n in N } then

Answer»

`X SUB Y`
`Y sub X`
X = Y
information not SUFFICIENT

ANSWER :A
Discussion
8666.

Assertion (A) : If one root of x^(2)- (3+2i)x+ (1 + 3i) = 0is 2+ i then the other root is 2-i Reason (R) : Imaginary roots (if occur) of a quadratic equation occurs in conjugate pairs only if the coefficients Q.E. are all real.

Answer»

Both A, R are TRUE and R explain Assertion
Both A, R are true but R does't explain A
A is true R is false
A is false R is true.

Answer :D
Discussion
8667.

Find the domain and range of the function f(x) = (sqrt(x + 4) - 3)/(x - 5)

Answer»


ANSWER :`[-4, OO)- {5}, (0, 1/6 UU (1/6, 1/3]`
Discussion
8668.

If the foot of perpendicular drawn from the point (2, 5, 1) on a line passing through (alpha, 2alpha, 5)" is "((1)/(5),(2)/(5),(3)/(5)), then alpha is equal to

Answer»

`(19)/(9)`
`(11)/(570)`
`(57)/(54)`
`(1)/(25)`

Answer :D
Discussion
8669.

A solution is to be kept between 77^@ F and 86^@ F . The range of temperature in degree celsius (C), if the Celsius /Fahrenheit (F) conversion formula is F = 9/5 C + 32is

Answer»

`20 LT C lt 25`
`20 lt C lt 30`
`20 lt C lt 24`
`30 lt C lt 33`

Answer :B
Discussion
8670.

If two lines are perpendicular to a third line, then the direction ratios of the two lines are proportional.

Answer»


ANSWER :F
Discussion
8671.

The locus represented by xy+yz=0 is

Answer»

1.a PAIR of perpendicular LINES
2.a pair of PARALLEL lines
3.a pair of parallel planes
4.a pair of perpendicular planes

ANSWER :D
Discussion
8672.

Pedal Triangle of a Triangle: Let Delta ABC be any triangle and let D, E, F be the feet of perpendiculars from the vertices A, B, C on the opposite sides BC, CA, AB respectively, then the triangle DEF is known as Pedal triangle of ABC. H is the orthocentre of the Delta ABC. We note that angle HDC= angle HEC=90^(@)' therefore angle HDE= angle HCE =90^(@) -A. Simillarly angle HDF =angle HBF=90^(@)-A. Hence, angle FDE=180^(@)-2A. Identically we can find angle DEF = 180^(@)-2B and angle EFD=180^(@) -2C. Thus, the angles of Pedal triangle are 180^(@)-2A, 180^(@) -2B, 180^(@)-2C. Further in Delta BFD, angle FDB=90^(@)-(90^(@)-A) =A, thus (FB)/(sin B)=(FB)/(sin A) therefore FD=(sin B)/(sin A) (BC cos B) = (a sin B cos B)/(sin A) = 2R sin B cos B=b cos B. Similarly, EF=a cos A and DE =c cos C. Thus, the sides of pedal triangle are a cos A, b cos B and c cos C (or R sin 2A, R sin 2B, R sin 2C), where R is the circumradius of Delta ABC. In the above derivation, the triangle ABC is assumed an acute angled triangle. In case the triangle ABC be obtuse angled with A as obtuse angle, then, the angles of pedal triangle will be represented by 2A - 180^(@), 2B,2C andthe sides will be represented by -a cos A, b cos B, c cos C. The inradius of the pedal triangle of a tringle ABC is

Answer»

`R//2`
`R SIN "" A/2 sin ""B/2sin ""C/2`
`2R cos A cos B cos C`
`4R sin ""A/2 sin ""B/2 sin ""C/2 `

Answer :C
Discussion
8673.

If x_(1) = 3y_(1) + 2y_(2) -y_(3), "" y_(1)=z_(1) - z_(2) + z_(3) x_(2) = -y_(1) + 4y_(2) + 5y_(3),y_(2)= z_(2) + 3z_(3) x_( 3)= y_(1) -y_(2) + 3y_(3),""y_(3) = 2z_(1) + z_(2) espress x_(1), x_(2), x_(3) in terms of z_(1) ,z_(2),z_(3).

Answer»


Solution :Since, ` X_(1) = 3y_(1) + 2y_(2) - y_(3)`
`rArr [x_(1)] = [(3,2,-1)] [[y_(1)],[y_(2)],[y_(3)]]`
Putting the values of `y_(1), y_(2), y_(3), ` we GET
`[x_(1)] = [(3,2,-1)] [[z_(1)-z_(2)+z_(3)],[0+z_(2)+3z_(3)],[2z_(1)+z_(2)+0]]`
`= [(3,2,-1)] [[1,-1,1],[0,1,3],[2,1,0]][[z_(1)],[z_(2)],[z_(3)]]`
`=[(3+0-2,-3+2-1,3+6+0)][[z_(1)],[z_(2)],[z_(3)]]`
`=[(1,-2,9)][[z_(1)],[z_(2)],[z_(3)]]`
`[x_(1)]= [z_(1)-2z_(2)+9z_(3)]`
`therefore x_(1) = z_(1) - 2x_(2) + 9z_(3) ""...(i)`
Further, `x_(2) = -y_(1) + 4y_(2) + 5y_(3) `
`rArr [x_(2)] = [(-1, 4,5)][[y_(1)],[y_(2)],[y_(3)]]`
Putting the values of `y_(1),y_(2),y_(3)`, we get
`[x_(2)] = [(-1, 4,5)][[z_(1)-z_(2)+z_(3)],[0+z_(2)+3z_(3)],[2z_(1)+z_(2)+0]]`
` = [(-1, 4,5)][[1,-1,1],[0,1,3],[2,1,0]][[z_(1)],[z_(2)],[z_(3)]]`
` = [(-1+0+10, 1+4+5,-1+12+0)][[z_(1)],[z_(2)],[z_(3)]]`
` = [(9,10,11)][[z_(1)],[z_(2)],[z_(3)]]=[9z_(1)+10z_(2)+11z_(3)]`
Hence, `x_(2)=9z_(1)=10z_(2)+11z_(3)`...(ii)
Further, `X_(3) = y_(1)-y_(2)+2y_(3)`
therefore[x_(3)] = [(1,-1 ,3)][[y_(1)],[y_(2)],[y_(3)]]
Putting the values of`y_(1), y_(2), y_(3)` we get
`rArr [x_(3)] = [(1, -1,3)][[z_(1)-z_(2)+z_(3)],[0+z_(2)+3z_(3)],[2z_(1)+z_(2)+0]]`
`= [(1,-1,3)][[1,-1,1],[0,1,3],[2,1,0]][[z_(1)],[z_(2)],[z_(3)]]`
`= [(1-0+6,-1-1+3,1-3+0)][[z_(1)],[z_(2)],[z_(3)]]`
`= [(7,1,-2)][[z_(1)],[z_(2)],[z_(3)]]=[7z_(1)+z_(2)-2z_(3)]`
`therefore x_(3) = 7z_(1)+z_(2)-2z_(3)`...(iii)
Hence , from Eqs. (i), (ii) and (iii) we get
`x_(1) =z_(1) - 2z_(2) + 9 z_(3) , x_(2) = 9z_(1)+10z_(2) + 11z_(3), x_(3)=7z_(1)+z_(2)-2z_(3)`
Discussion
8674.

Consider a three dimensional Cartesian system with origin at O and three rectangular coordinate axes x,y and z-axis. Suppose that the distance between two points P and Q in the space having their coordinates (x _(1), y_(1), z _(1)) and (x _(2), y _(2), z _(2)) respectively be defined by the following formula d (P,Q) =|x_(2)-x_(1)|+ |y_(2)-y_(1)|+ |z _(2) -z_(1)| Although the rormula of distance between two points has been defined in a new way, yet the other definition remain same (like section formula, direction consines ets). So, in general equations of straight line in space, plane in spece remain unchanged. If l, m, n represent direction consines (if we can call it) of a vactor bar(OP), then which of the following relations holds?

Answer»

`L ^(2) + m ^(2) + N ^(2) =1`
`l+m+n =1`
`| l + m+ n|=1`
`|l| + |m| + |n| =1`

ANSWER :D
Discussion
8675.

The magnitudes of the gravitational field at distance r_(1)andr_(2) from the centre of a uniform sphere of radius R and mass M are F_(1)andF_(2) respectively. Then :

Answer»

`(F_(1))/(F_(2))=(r_(1))/(r_(2))ifr_(1)ltR andr_(2)ltR`
`(F_(1))/(F_(2))=(r_(2)^(2))/(r_(1)^(2))ifr_(1)gtR andr_(2)gtR`
`(F_(1))/(F_(2))=(r_(1))/(r_(2))ifr_(1)gtR andr_(2)gtR`
`(F_(1))/(F_(2))=(r_(1)^(2))/(r_(2)^(2))ifr_(1)ltR andr_(2)ltR`

Solution :`G={{:((GMR)/R_(3)rltR)/((GM)/(R^(2))rgeR):}`
`(A)r,r_(2)ltR" ":." "(F_(1))/(F_(2))=(r_(1))/(r_(2))`
`(B)r,r_(2)gtR" ":." "(F_(1))/(F_(2))=(r_(2)^(2))/(r_(1)^(2))""]`
Discussion
8676.

Resolve (x^(3))/((x-a)(x-b)(x-c)) into partial fractions.

Answer»


Answer :`:. (x^(3))/((x-a)(x-B)(x-C))= 1 + (a^(3))/((a-b)(a-c)(x-a))+(b^(3))/((b-a)(b-c)(x-b))+(c^(3))/((c-a)(c-b)(x-c))`
Discussion
8677.

Three groups A, B, C are contesting for positions on the board of directors of a company. The probabilities of their winning are 0.5, 0.3 and 0.2 respectively. If the group A wins the probability of introducing a new product is 0.7 and the corresponding probabilities for group B and C are 0.6 and 0.5 respectively. Find the probability that the new product will be introduced.

Answer»


ANSWER :`0.63`
Discussion
8678.

The numberof waysinwhich5 boy and 4girlssitarounda circulartableso thatnotwogirlssittogetheris

Answer»

`5!4!`
`5!3!`
`5!`
`4!`

ANSWER :A
Discussion
8679.

The volume occupied by 4.4 gram of CO_(2) at STP is :-

Answer»

22.4 L
2.24 L
0.224 L
0.1 L

Answer :A
Discussion
8680.

If 10. ""^(n)C_(2)=3. ""^(n+1)C_(3) find n.

Answer»


ANSWER :9
Discussion
8681.

Realising he needs money, Tintin reaches inside the bank situated on the island, and sees a row of lockers which start with 0 and go on till infinity. A locker can contain any number of coins. A coin is placed in the locker with index 7 (i.e. the 8th square). The aim is to move this coin to the locker with index 1. (i.e. the 2nd square) and all other squares empty. There are two rules to this: 1) Fission Rule: A coin may be replaced by a pair of coins by placing one in each of the immediately adjacent squares. Eg.Coin #3 can be replaced by Coin#2 and Coin#4 where Coin#(number) rep- resents coin in position with index number. 2) Fusion Rule: A pair of coins separated by exactly one intervening square can be replaced by a single coin in that middle square. Eg.Coin#2 and Coin#4 can be replaced by Coin#3. Minimum number of moves required to achieve our aim ?

Answer»

18
19
17
16

Solution : This puzzle seems rather difficult to solve by TRYING random moves that appear to GETONE CLOSER to the solution. However, consider the board a sequence of integers, each beingthe number of pennies at that location, and the moves as adding or SUBTRACTING (+1, ­1, +1)to three consecutive values.Then by inspection we can come up with a solution, not worrying about whether the number ofpennies is always positive, by adding the columns:
000000+1 (start)
0000­1 +1­1
000­1 +1 ­10
0 +1­1 +1000
+1­1 +10000
­­­­­­­­­­­­­­­­­­­­­­­­­­­
+1000000 (end) 
This gives you the four critical moves that must be in any solution. However, applying themdirectly is illegal. [But you can] just [keep] SPLITTING the left penny (7 times), then [do the] “critical4 moves” and you come up with the mirror image position, so you now combine to the finalposition. Ergo,
0 0 0 0 0 0 0 1 0
0 0 0 0 0 0 1 0 1
0 0 0 0 0 1 0 1 1
0 0 0 0 1 0 1 1 1
0 0 0 1 0 1 1 1 1 
0 0 1 0 1 1 1 1 1 
0 1 0 1 1 1 1 1 1
1 0 1 1 1 1 1 1 1
1 1 0 2 1 1 1 1 1lt­­+1 ­1 +1
1 1 1 1 2 1 1 1 1lt­­+1 ­1 +1
1 1 1 1 1 2 0 1 1 
1 1 1 1 1 1 1 0 1lt­­­1 +1 ­1
1 1 1 1 1 1 0 1 0lt­­­1 +1 ­1
1 1 1 1 1 0 1 0 0
1 1 1 1 0 1 0 0 0
1 1 1 0 1 0 0 0 0
1 1 0 1 0 0 0 0 0
1 0 1 0 0 0 0 0 0
0 1 0 0 0 0 0 0 0
Discussion
8682.

Ifthecoefficientsofr^(th)and( r +1 ) ^(th)termsintheexpansionof(3 + 7x ) ^(29)areequal , then r isequalto

Answer»

14
15
18
21

Solution : ` (3 +7x ) ^(29) `
Theco- efficientof`r^(th ) `term=Co - efficient` (r + 1 ) ^(th) `term
`rArr29 _(c_(r-1)) ( 3) ^(29-r + 1 )( 7) ^( r - 1 )= 29_(c _r ) (3) ^(29 - r )= (7) ^(r ) `
` rArr(29 _(c_r )) /(29 _ (c _ (r - 1 )) )= (3 ^( 29 - r + 1 ) )/(3 ^(29 - r ))XX ( 7 ^(r - 1 )) /( 7 ^ (r )) `
` rArr(29 -r+ 1 ) /(r ) = (3 ) /(7)""[ because(n _ c _ r ) /(n _(c_(r - 1 ))) = ( n - r+ 1 ) /( r ) ] `
`= (30- r)/( r )=(3 ) /(7) `
` 210-7r=3r `
`210=10 r`
`thereforer= 21 `
Discussion
8683.

Consider a function f whose domain is [-3, 4] and range is [-2, 2] with following graph. If h(x)=|f(x)-(3)/(2)| has range [e, f] and n be number of real solutions of h(x)=(1)/(4), " then " (n+e+2f) is

Answer»

8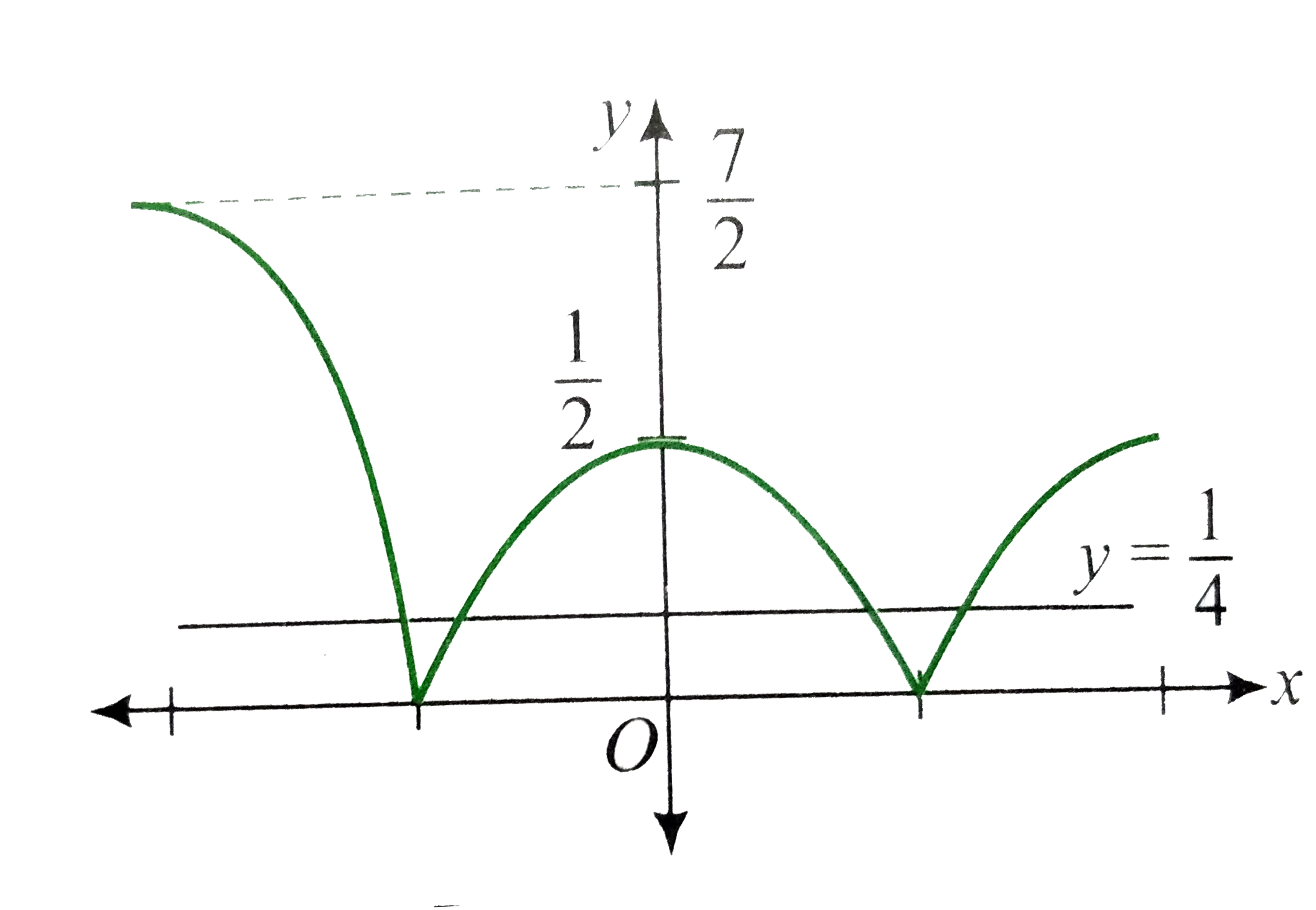
9
10
11

Solution :
Range of `h(X)=[0, (7)/(2)]`
Number of solutions of `h(x)=(1)/(4) " is " n=4.`
` :. (n+e+2f)=4+0+7=11.`
Discussion
8684.

If the length of the subtangent at any point of a curve is constant , then the curve is

Answer»

`y^(2) = 2KX + C`
`y = be^(X//a)`
`x^(2) = 2ky + c`
none

Answer :B
Discussion
8685.

For L.P.P, maximize z=4x_(1)+2x_(2) subject to

Answer»

`3x_(1)+2x_(2)ge9,x_(1)-x_(2)le3,x_(1)ge0,x_(2)ge0` has. . .
infinite number of optimal solutions
unbounded solution
no solution

Solution :We have, maximise `z=4x_(1)+2x_(2)`
SUBJECT to constracts, `3x_(1)+2x_(2)ge9,x_(1)-x_(2)le3,x_(1)ge0,x_(2)ge0`
On taking GIVEN constraints as EQUATION, we GET the following graphs
Discussion
8686.

Check the points where the constant function f(x)= k is continuous

Answer»


ANSWER :F is continious for REAL NUMBER
Discussion
8687.

IF the sum of the roots of ax^2+bx+c=0 is equal to the sum of the squares of the roots, then……..

Answer»

A.P
G.P
H.P
none

Answer :A
Discussion
8688.

If [1" "x" "1][{:(1,3,2),(0,5,1),(0,3,2):}][{:(1),(1),(x):}]=O, then x=.....

Answer»

`(-9+-sqrt(35))/(2)`
`(-7+-sqrt(53))/(2)`
`(-9+-sqrt(53))/(2)`
`(-7+-sqrt(35))/(2)`

ANSWER :C
Discussion
8689.

For all real values of k, the point which lies on the polar of (k,k+1) with respect to the circle x^(2)+y^(2)+4x-8y-5=0 " is "

Answer»

`(3,-1)`
`(3,1)`
`(2,-2)`
`(2,3)`

ANSWER :A
Discussion
8690.

IF k^(3) is divisible by 240, what is the least possible value of integer k?

Answer»

12
30
60
120

Answer :C
Discussion
8691.

The locus of the midpoints of the focal chords of the parabola y^(2)=6x which pass through a fixed point (9,5) is

Answer»

`y^(2)+5y+3x+27=0`
`y^(2)+5y-3x+27=0`
`y^(2)+5y-3x+27=0`
`y^(2)-5y-3x-27=0`

ANSWER :C
Discussion
8692.

1 + 1/3 + (1.3)/(1.2) .(1)/(3^2) + (1.3.5.)/(1.2.3).(1)/(3^3) + ……oo =

Answer»

`SQRT2`
`sqrt3`
`sqrt5`
`(1)/(2sqrt3)`

ANSWER :B
Discussion
8693.

If tan(B-C/2)=xcotA/2,then x =

Answer»

`a-B/(a+b)`
`b-c/(b+c)`
`c-a/(c+a)`
None

Answer :B
Discussion
8694.

Let f(x) = sin^(-1)|sin x| + cos^(-1)( cos x) . Which of the following statement(s) is / are TRUE ?

Answer»

`f(f(3)) = pi`
f (X) isperiodic with fundamental period `2 pi`
f (x) is neither even nor ODD
RANGE of f(x) is `[0,2pi]`

Answer :A::B
Discussion
8695.

Differentiate sin(cos x^(2)) with respect to x

Answer»


ANSWER :`-2x SIN X^(2) cos (cos^(2))`
Discussion
8696.

Consider a three dimensional Cartesian system with origin at O and three rectangular coordinate axes x,y and z-axis. Suppose that the distance between two points P and Q in the space having their coordinates (x _(1), y_(1), z _(1)) and (x _(2), y _(2), z _(2)) respectively be defined by the following formula d (P,Q) =|x_(2)-x_(1)|+ |y_(2)-y_(1)|+ |z _(2) -z_(1)| Although the rormula of distance between two points has been defined in a new way, yet the other definition remain same (like section formula, direction consines ets). So, in general equations of straight line in space, plane in spece remain unchanged. Locus of point P if d (O,P) = k, where ,k is a positive constnat number, represents

Answer»

a sphere of radius K
a set of eight planes FORMING an octhedron
a set of eight planes forming HEXAGONAL PRISM
an infinite cylinder of radius k

Answer :B
Discussion
8697.

Consider a three dimensional Cartesian system with origin at O and three rectangular coordinate axes x,y and z-axis. Suppose that the distance between two points P and Q in the space having their coordinates (x _(1), y_(1), z _(1)) and (x _(2), y _(2), z _(2)) respectively be defined by the following formula d (P,Q) =|x_(2)-x_(1)|+ |y_(2)-y_(1)|+ |z _(2) -z_(1)| Although the rormula of distance between two points has been defined in a new way, yet the other definition remain same (like section formula, direction consines ets). So, in general equations of straight line in space, plane in spece remain unchanged. Let A be a point (5,2,3) in the given reference system. Then locus of the point P in the fiest octant satisfying the equation d (O,P) =d (A, P) does not contain

Answer»

any of the COORDINATES AXES
any of the coordinates planes
any PLANE parallel to coordinates axes planes
any plane parallel to coordinates

ANSWER :D
Discussion
8698.

Find the values of each of the following : "tan"1/2["sin"^(-1)(2x)/(1+x^(2))+"cos"^(-1)(1-y^(2))/(1+y^(2))],|x|lt1,ygt0 and xylt1

Answer»


ANSWER :`(x+y)/(1-xy)`
Discussion
8699.

If (x+1/x+1)^(6)=a_(0)+(a_(1)x+(b_(i))/(x))+(a_(2)x^(2)+(b_(2))/(x^(2)))+"...."+(a_(6)x^(6)+(b_(6))/(x^(6))), then

Answer»

`a_() = 141`
`a_(5) = 6`
`underset(i=1)OVERSET(6)sum a_(i) + b_(i) = 588`
`underset(i=1)overset(6)suma_(i) + b_(i) = 3^(6)`

Solution :`(x+1/x+1)^(6)=underset(r=0)overset(n)sum.^(6)C_(r)(x+1/x)^(r)`
(1) `a_(0) = 1 +.^(6)C_(2)..^(2)C_(1) + .^(6)C_(4)+.^(4)C_(2)+.^(6)C_(6).^(6)C_(3)`
`= 1+30+90+20 = 141`
(2) `a_(5) = .^(6)C_(5) xx` Coefficient of `x^(5)` in `(x+1/x)^(5)`
`= .^(6)C_(5).^(5)C_(0) = 6`
(3) Putting , `x = 1`
`a_(0) + (a_(1) + b_(1)) + (a_(2)+b_(2))= 3^(6)`
`:. underset(i=1)overset(6)sum(a_(i)+b_(i)) = 3^(6) - 141 = 588`
Discussion
8700.

ABCD isa rhombus with AC=2BD. Diagonals AC and BD intersect at P.E_(1),E_(2),E_(3) and E_(4) are four ellipes passing through P and their foci are A andB, B and C, C and D and D and A, respectively . If for i=1,2,3,4,e_(i)are the eccentricities fo E_(i), then

Answer»

`e_(i)=e_(3)`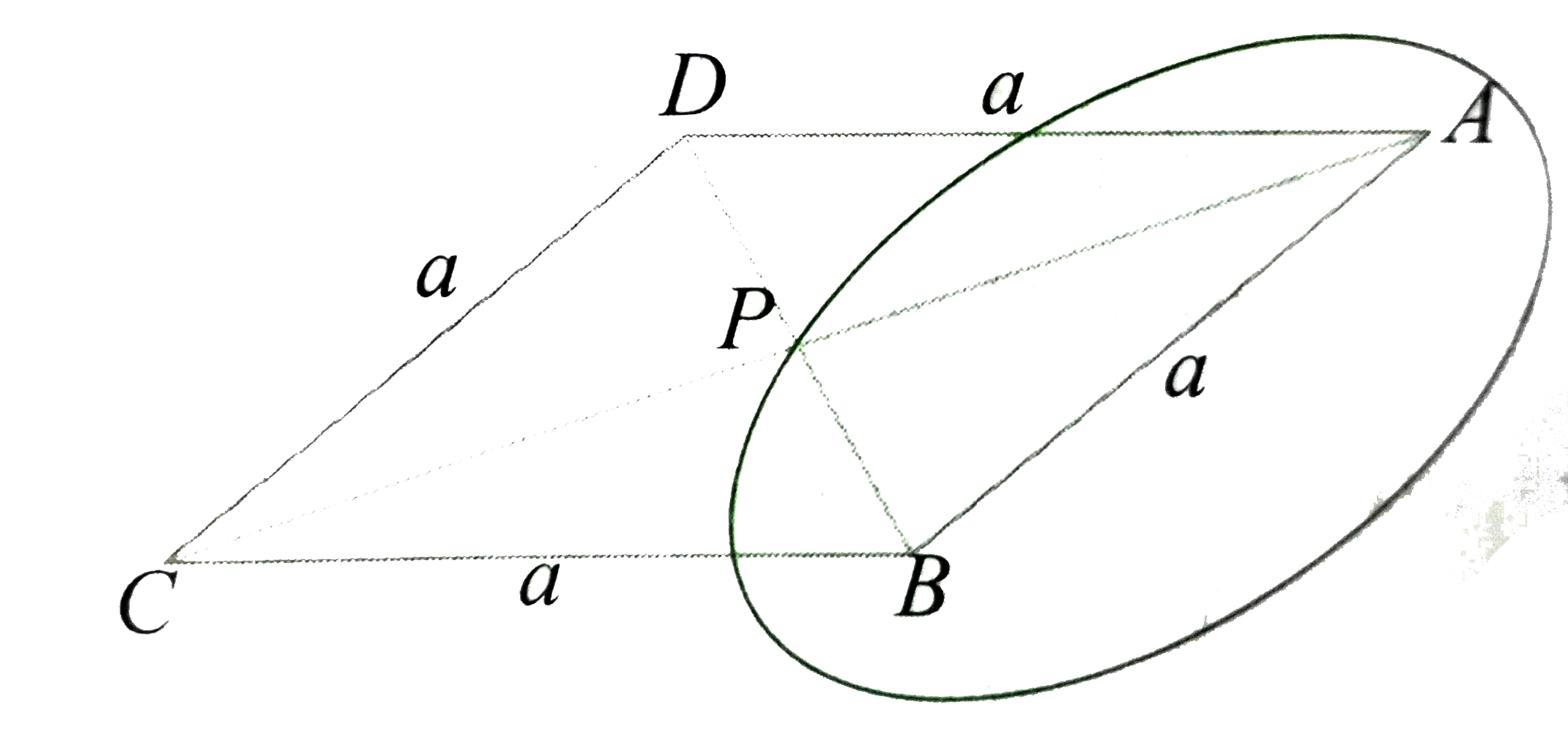
`e_(2)=e_(4)`
`e_(1)=2e_(2)`
`e_(1)=e_(2)`

SOLUTION :
AB=BC=CD=DA=
Since `DeltaPAB, DeltaPBC, DeltaPCD, DeltaPDA` are congruent,
`e_(1)=e_(2)=e_(3)=3_(4)=(a)/(PA+PB)`
Discussion