InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 8702. |
A reversible reaction is which :- |
|
Answer» PROCEEDS in ONE direction |
|
| 8703. |
Consider tetrahedron with faces F_(1),F_(2),F_(3),F_(4). Let vec(V_(1)),vec(V_(2)),vec(V_(3)),vec(V_(4)), be vectors, whose magnitudes are respectively equal to areas ofF_(1),F_(2),F_(3),F_(4) & whose directions are perpendicular to their faces in outward directon, then |vec(V_(1))+vec(V_(2))+vec(V_(3))+vec(V_(4))| |
|
Answer» 1 DR's of DC `(2lambda-1,4lambda-2,5lambda-5)` `DC_|_"line"` `THEREFORE LAMBDA=(7)/(9)impliesDR's"of"DC ((5)/(9),(10)/(9),(-10)/(9))` EQUATION of plane : `(5)/(9)(x-3)+(10)/(9)(y-1)-(10)/(9)(z-2)=0` `therefore` Equation of plane `x+2y-2z=1` 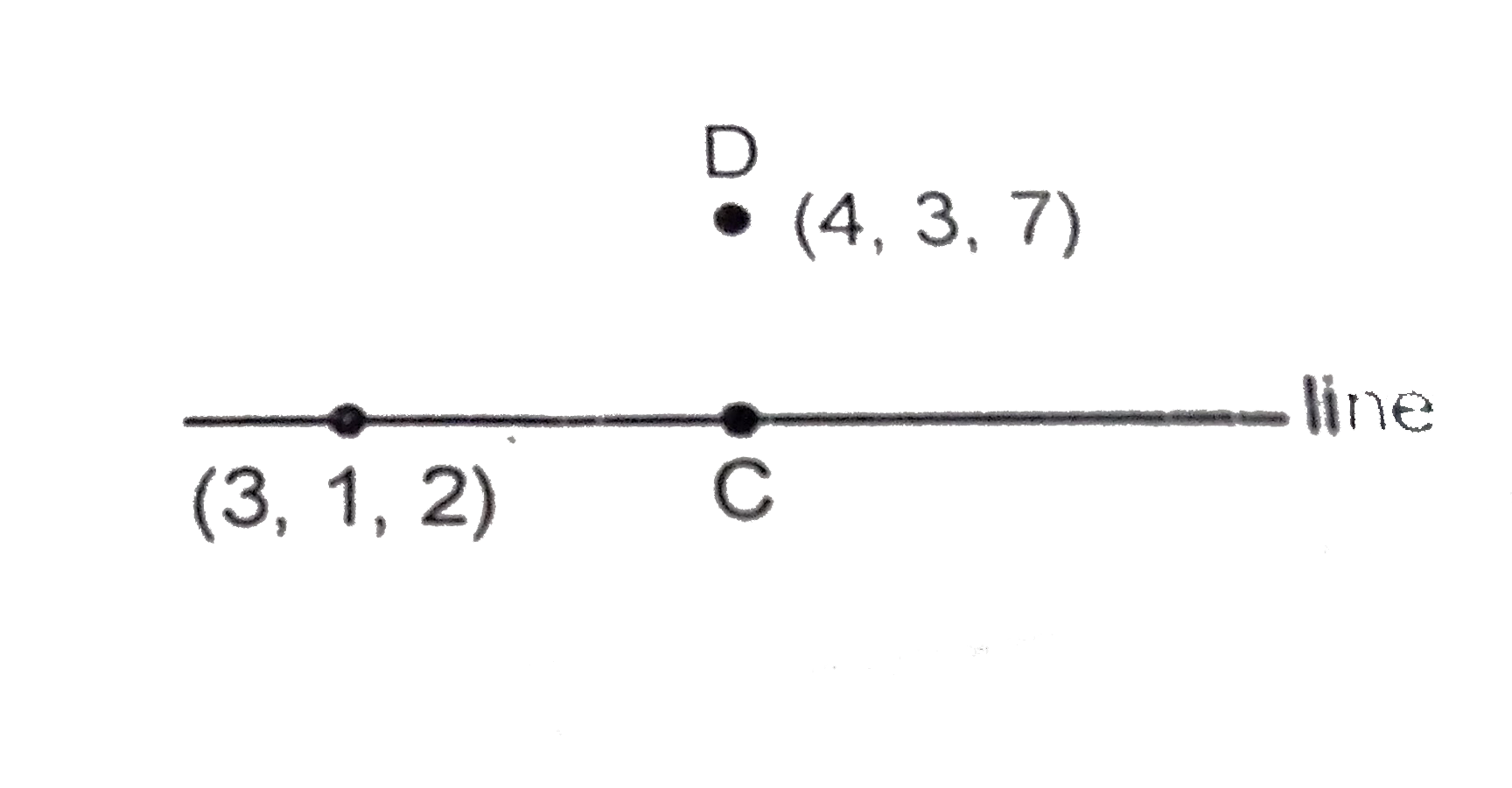
|
|
| 8704. |
If C_(r)= ""^(n)C_(r), then C_(0)+C_(4)+C_(8)+C_(12)+cdots= |
|
Answer» `(2^((n)/(2))[SIN""(NPI)/(4)+2^(n/(2)-1)]]/(2)` |
|
| 8705. |
A:In Delta ABC, if r_1,r_2,r_3 are in H.P. then r_2//r=1//3 R: In DeltaABC,1/r_1+1/r_2+1/r_3=2/r |
|
Answer» A is true, R is true and R is CORRECT EXPLANATION of A |
|
| 8706. |
If m = ( 2013) ! then the value of (1)/(log_(2)m) + ( 1)/( log_(3)m ) + "........"+ ( 1)/( log_(2013)m) is equal to |
| Answer» Answer :A | |
| 8707. |
Evaluate the integral underset(0)overset(1)int (log(1+x))/(1+x^(2))dx |
|
Answer» `PI/4 LN 2` |
|
| 8708. |
If ina triangle ABC , a=15, b= 36, c = 39 thensin"" (C )/(2)= |
|
Answer» `( SQRT(3))/(2)` |
|
| 8709. |
On all chords (parallel to one and the same direction) a circle of radius R symmetrical parabolic segments of the same altitude h are constructed. The planes of the segments are perpendicular to the plane of the circle. Find the volume of the solid thus obtained |
|
Answer» |
|
| 8710. |
Defineeach of thefollowing: "(i)injective function """"(ii) surjectivefunction " "(iii) bijective function """"(iv) many -onefunction" "(v) intofunction """ Give anexampleof each typeof functions. |
|
Answer» SOLUTION : (i) `f : N to N : f (x) =2x` isinjectivefunctionas ` f(x_(1))=f(x_(2))rArr 2x_(1)=2x_(2)rArr x_(1) = x_(2)` (ii)`A ={1, -1, 2,3}" and"= { 1, 4,9}` Then`f : A toB : f(x) = x^(2)` is surjectivesince eachelementof Bhas atleastonepre -imagein A. (III) Let E be theset of all evennaturalnumbers Then`f N to E : f(x) =2x` is one-oneand ONTO . f is one-onesince `f (x_(1)) = f(x_(2))rArr2x_(1) = 2x_(2) rArr x_(1) =x_(2)` f is ontosince foreach`y in E` thereexists` (1)/(2) y in N ` such that ` f ((1)/(2)y) =y` (iv)Examplegiven in (ii)is many -one . (v)Let `A = {1,2,3} " and" B = {1,4,9,16}` Then `f : A toB : f (x) = x^(2)` is anintofunction sincerange(f) = `{1,4,9 } sub B` |
|
| 8711. |
int (1)/(2x^(2)-3)dx= |
|
Answer» `(1)/(SQRT(6)) "LOG " |(sqrt(2)X - sqrt(3))/(sqrt(2) x + sqrt(3)) | + C ` |
|
| 8712. |
int ((x+3)/((x+4)^(2)))e^(x)dx=.....+C |
|
Answer» `E^(X)((1)/(x+4))` |
|
| 8713. |
Given three non-coplanar vectors OA=a, OB=b,OC=c. Let S be the centre of the spheres passing through the points, O,A,B,C if OS=x, then: |
|
Answer» X must be LINEAR combinationof a,B and c |
|
| 8714. |
Draw the graph of y= [x]+ sqrt(x-[x]), where[*] denotes the greatest ineger function. |
|
Answer» Solution :`y= f(X) = [x] + sqrt(x-[x])` For `0 le x LT 1, y = sqrtx`,the graph of which is PART of parabola `y^(2)=x` lying above the x-axis. For `1 le x lt 2, y=1 + sqrt(x-1)`, the graph of which is part of the parabola `(y-1)^(2)=x-1` lying above the axis of the parabola `y=1`. THUS, all the branches of `y=f (x) ` are part of different parabolas. Also we can see that in each interval `y= f(x)` is an increasing function. Hence the graph of`y= f(x)` is as SHOWN in the following figure. 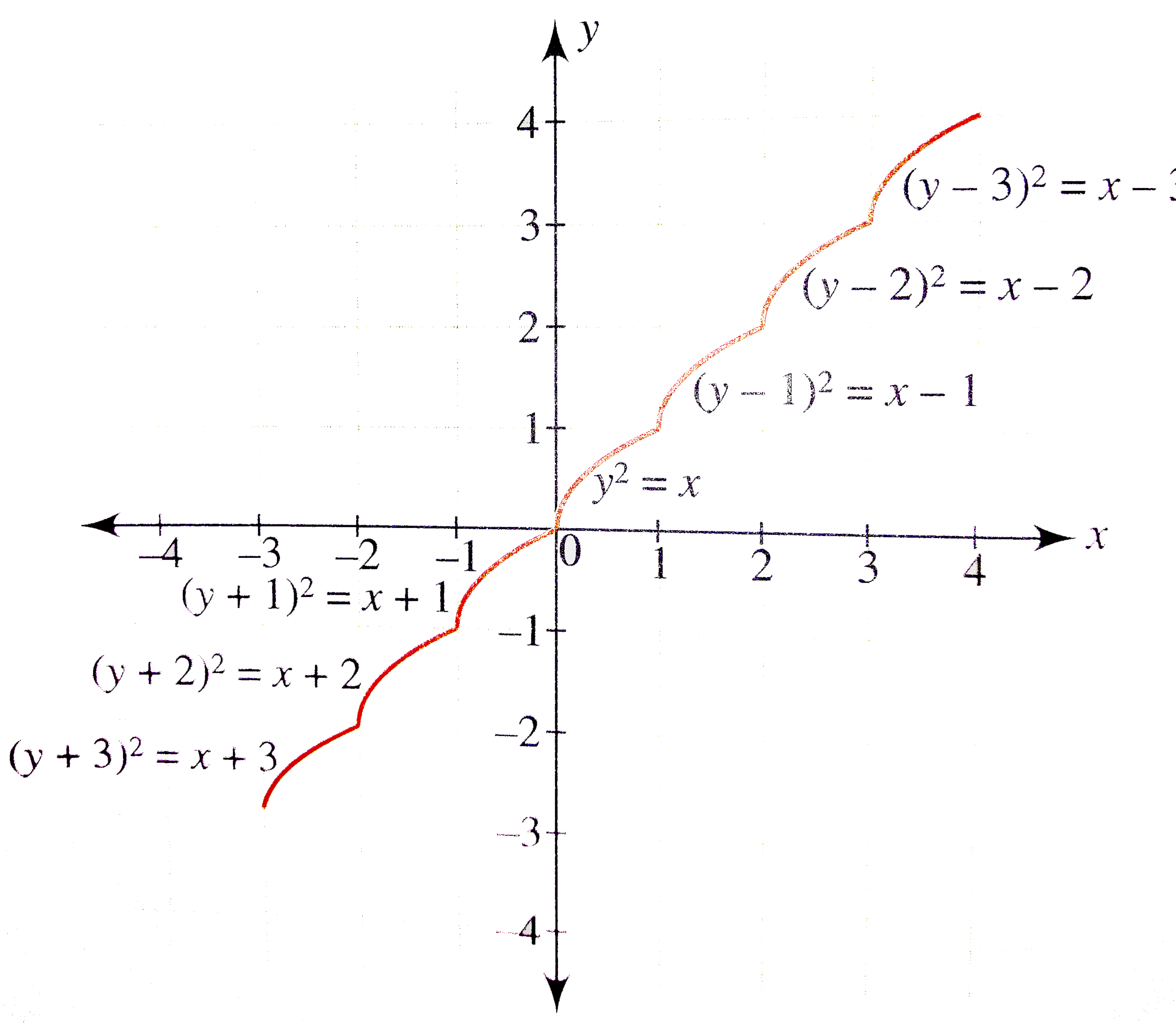
|
|
| 8715. |
IFS=overset ( m) sum"" ^(n+r ) C_(k),then |
|
Answer» `S+""^(N)C_(K+1) =-""^(n)C_(K+1)` |
|
| 8716. |
If the equation ................ |
|
Answer» `:. h^(2)=ab` i.e. `(6/2)^(2)=3 m` i.e. `m=3` |
|
| 8717. |
int_(1//3)^(1) ((x-x^(3))^(1//3))/(x^(4))dx= |
|
Answer» 4 |
|
| 8718. |
If (x^(4))/((x-1)(x+2))=(1)/(3(x-1))-(16)/(3(x+2))+x^(2)-x+k then k= |
|
Answer» 0 |
|
| 8719. |
If a parabola passess through the points (-2, 1), (1, 2) and (-1, 3) having horizontal axis, then the length of the latus rectum of that parabola is |
|
Answer» 5 |
|
| 8720. |
If in A.P., 3rd term is 18 and 7 term is 30, then find sum of its first 17 terms |
|
Answer» |
|
| 8722. |
Expand the expression (2x - 3)^(6). |
|
Answer» |
|
| 8723. |
Solution of the differential equation (dy)/(dx)=(1+y^(2))/(1+x^(2)) is |
|
Answer» 1+xy+C (y-x)=0 |
|
| 8724. |
By using the properties of definite integrals, evaluate the integrals int_(0)^(pi/2)cos^(2)xdx |
|
Answer» |
|
| 8725. |
If a, b, c arein AP amd b, c, a are in GP , thenshow that c, a, b are in H.P. Finda : b : c . |
|
Answer» |
|
| 8726. |
If Z is a complex number such that Z=-overlineZ,then |
|
Answer» Z is any complex number |
|
| 8727. |
There are 4 mangoes, 3 apples 2 oranges in bag, fruits of the same variety being identical. In how many different ways can a selection of fruits be made if atleast one mango is to be selected. |
|
Answer» |
|
| 8729. |
Evaluate the following lim_(xto0)((3+x)^3-27)/x |
|
Answer» SOLUTION :`lim_(xto0)((3+X)^3-27)/x` `=lim_(xto0)(27+x^3+27x+9x^2-27)/x` `=lim_(xto0)(x^3+27x+9x^2)/x` `=lim_(xto0)(x(x^2+27+9x))/x` `=lim_(xto0)(x^2+9x+27)=27` |
|
| 8730. |
If the system of equation (b+c)x+ay+a^(2)z=0,(c+a)x+by+b^(2)z=0,(a+b)x+cy+c^(2)z=0 has a non trivial solution and a ne b ne c prove that a+b+c=0 |
|
Answer» |
|
| 8731. |
Consider the sequence in the form of group (1),(2,2)(3,3,3),(4,4,4,4),(5,5,5,5,5…..) The 2000^(th) term of the sequence is not divisible by |
|
Answer» 3 Let us write the terms in the groups as follows: 1,(2,2),(3,3,3),(4,4,4,4),… CONSISTING of 1,2,3,4,.. Terms. Let 2000th term fall in nth group. Then, `((n-1)n)/2lt2000le(n(n+1))/2` or n(n-1)`lt4000len(n+1)` Let us consider, `n(n-1)lt4000` or `n^(2)-n-4000lt0` or `nlt(1+sqrt(16001))/2` r `nlt64` We have `n(n+1)ge4000` or `n^(2)+n-4000ge0` or `nge63` That means 2000th term falls in 63rd group, which means that the 2000th term is 63. Now, the total NUMBER of terms up to 62ND group is `(62xx63)//2=1953`. Hence, the sum of first 2000 terms is `1^(2)+2^(2)+..+62^(2)+63(2000-1953)` `=(62(63)125)/6+63xx47=84336` Sum of the remaining terms=`63xx16=1008`. |
|
| 8732. |
If 36, 84, 126 are three successive binomial coefficients in the expansion of (1+x)^(n), find n. |
|
Answer» |
|
| 8733. |
If bar(a) and bar(b) are adjacent sides of a rhombus, then bar(a).bar(b)=0. |
|
Answer» |
|
| 8734. |
Consider the determinant Delta=|[0,2,6],[1,5,0],[3,7,1]|Write the minors of the element in the first column ? |
|
Answer» SOLUTION :The MINORS are GIVEN below: `M_11=|[5,0],[7,1]|=5-0=5,` `M_21=|[2,6],[7,1]|=2-42=-40` `M_31=|[2,6],[5,0]|=0-30=-30` |
|
| 8735. |
Choose the correct answer. If theta is the angle between two vectors veca"and"vecb, then veca.vecb ge 0 only whena)0 lt theta lt pi/2b)0 le theta le pi/2c)0 lt theta lt pid) 0 le theta le pi |
|
Answer» `0 LT THETA lt pi/2` |
|
| 8736. |
What is the interval in which log_5xis increasing ? |
| Answer» Solution :LET `y=log_5x=(In5)/(In5)RARR(DY)/dx=1/(xIn5)` y is decreasing for `(dy)/dxlt0rArrxlt0 | |
| 8737. |
A bag contains 4 white balls and 3 black balls. If two balls are drawn at random, then mean of number of white balls is |
| Answer» Answer :A | |
| 8738. |
If two cards are drawn from pack 52 cards at random, then find the probability of getting both red or both kings. |
|
Answer» |
|
| 8739. |
int_(0)^(2a) f(x) dx = 2 int_(0)^(a) f (x) dx if |
|
Answer» `F(2a-X) =f(x)` |
|
| 8740. |
If f :Rto R is definedby f (x)f(x)= [ x -3]+ | x -4| forx inR thenlim_(x to 3)f(x)is equal to |
| Answer» Answer :C | |
| 8741. |
Solvexsec((y)/(x))*(y dx+x dy)=y" cosec"((y)/(x))*(x dy-y dx) |
|
Answer» |
|
| 8742. |
If alpha, beta are the roots of the equation x^(2)+7x+12=0, then the equation whose roots are (alpha+beta)^(2) and (alpha-beta)^(2) is |
|
Answer» `X^(2)+50x+49=0` |
|
| 8743. |
I : If a,b,c,d are four vectors then [b c d] a + [c a d] b + [a b c] c = [a b c]d II : The points with position vectors a,b,c,d are coplanar then [a b d] + [b c d] + [c a d] = [a b c] |
|
Answer» only I is ture |
|
| 8744. |
If alpha, beta ,gamma are roots of a cubic equationx^(3) + 2x^(2) - 3x - 1 = 0, then sum alpha^(-5) = |
|
Answer» -365 |
|
| 8745. |
Evaluate: int(x^2)/(x^4+x^2-2)\ dx |
|
Answer» |
|
| 8746. |
Derivative of tan^(-1)2xsqrt(1-x^(2))/(1-2x^(2))w.r.t.sec^(-1)" "(1)/(2x^(2)-1)" at "x=(1)/(2) |
| Answer» Answer :C | |
| 8747. |
IF A={:[(1,2,5),(1,-1,-1),(2,3,-1):}] find A^-1 Hence solve the following system of equations: x+2y+5z=10,x-y-z=-2,2x+3y-z=-11 |
|
Answer» |
|
| 8748. |
Area bounded by the curve y=x^3, the x-axis and the ordinates x = -2 and x = 1 is |
|
Answer» -9 |
|
| 8749. |
Write relations in tabular form and determine their type for R={(x,y):x "divides" y} on A ={1,2,3,4,5,6} |
|
Answer» SOLUTION :R`={(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,2),(2,4),(2,6),(3,3),(3,6),(4,4),(5,5),(6,6)}` R is REFLEXIVE TRANSITIVE but not SYMMETRIC. |
|
| 8750. |
Find for what values of a and b the system of linear equation.x+2y+2z=5 , 2x+5y+3z=10 and 3x+y+lambda z=mu has (i) no solution,(ii)a uniquesolution, (iii)an infinite no of solution. |
|
Answer» |
|