Explore topic-wise InterviewSolutions in .

This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.

8801.

If |x| lt 1 then coefficient of x^(2) in (log(1+x))/((1-x)^(2)) is

Answer»

`(3)/(2)`
2
`-(1)/(2)`
4

Answer :A
Discussion
8802.

If (1, 0, 3), (2, 1, 5), (-2, 3, 6) are the mid-points of the sides of a tringle, then the centroid of the triangle is

Answer»

`(1/3, 4/3, -14/3)`
`(1/3, 4/3, 14/3)`
`(1/3, -4/3, 14/3)`
`(-1/3, 4/3, 14/3)`

ANSWER :B
Discussion
8803.

This section contains 1 paragraph. Based on paragraph, there are 3 questions. Each question has 4 choices (1), (2), (3), (4) out of which only one is correct Q. If F(x) is continuous at x=-1, then

Answer»

`a+B=-2`
`a-b=3`
`a^(2)=b^(2)+5`
`a+b=5`

ANSWER :D
Discussion
8804.

This section contains 1 paragraph. Based on paragraph, there are 3 questions. Each question has 4 choices (1), (2), (3), (4) out of which only one is correct Q. if F(x) is continuous at x=+-1, then f(x)=g(x) has

Answer»

IMAGINARY roots
both the roots positive
roots of opposite sign
both the roots negative.

Solution :`F(x)={{:(f(x),-1ltxlt1),(g(x),xge1orxlt-1),((f(-1)+g(-1))/(2),x=-1),((f(1)+g(1))/(2),x=1):}`
for continuity at `x=1`
`f(1)=g(1)=(f(1)+g(1))/(2)`
`implies1+a+3=1+bimpliesb=a+3`
Similarly we can check for other questions.
Discussion
8805.

Ifa = cos "" (4pi)/(3) + isin "" (4pi)/(3) then ((1 + a)/(2))^(3n) =

Answer»

`((1)/(2))^(3n)`
`(- (1)/(2))^(3n)`
`(- (1)/(2))^(N)`
`((1)/(2))^(n)`

ANSWER :B
Discussion
8806.

Letf (x)= [x] , where[x]denotesthegreaterinteger lessthanorequalto x. ifa = sqrt(2011 ^2 +2012 ) then thevalueof f(a) isequalto

Answer»

175
152
176
151

Answer :D
Discussion
8807.

Find the number of terms in the expansion of ((3a)/(4)+(b)/(2))^(9)

Answer»


SOLUTION :N/A
Discussion
8808.

A line L is passing through the point A whose position vector is hati+2hatj-3hatk and parallel to the vector 2hati+hatj+2hatk. A plane pi is passingthrough the points hati+hatj+hatk, hati-hatj-hatk and parallel to the vector hati-2hatj. Then, the point where this plane pi meets the line L is

Answer»

`(1)/(7)(15hati+18hatj-9hatk)`
`7hati+hatj-19hatk`
`3hati+3hatj-hatk`
`2hati-hatj+hatk`

ANSWER :A
Discussion
8809.

If x = sqrt(a^(sin^(-1)t)), y= sqrt(a^(cos^(-1)t)), show that (dy)/(dx)= -(y)/(x)

Answer»


ANSWER :`-(y)/(X)`
Discussion
8810.

Which number is larger (1,1)^(100000) or 10,000 ?

Answer»


ANSWER :`(1.1)^(100000) GT 10,000`
Discussion
8811.

A tower BCD surmounted by a spire DE stands on a horizontal plane. At the extremity A of a horizontal line BA it is found that BC and DE subtend equal angles. If BC = 3 m, CD = 28 m and DE = 5 m, then BA is equal to

Answer»

`SQRT(18 XX 93)`
`sqrt(36 xx 93)`
`sqrt(34 xx 93)`
`sqrt(34 xx 36)`

ANSWER :A
Discussion
8812.

If A=(1)/(9)[[-8,1,a],[4,4,7],[b,-8,4]] is orthogonal find a, b hence find A^(-1).

Answer»


ANSWER :`A^(-1)=(1)/(9)[[-8,4,1],[1,4,-8],[4,7,4]]`
Discussion
8813.

Three copy machines- A,B and C- copy at the same rate and will all be used to make copies of a report. At 8:00 a.m., all 3 machines begin copying Machine A breaks down at 10:00 a.m. And is back in service at 1:00 p.m. Machine B breaks down at 12:00 p.m. (noon) and begins copying again at 3:00 p.m. All 3 machines finish copying at 5:00 p.m. when the copying of the report is complete. One of the following graphs showns n, the numbers of copies made, as a function of t, the time at any given point during the copying. Which graph is it?

Answer»




ANSWER :A
Discussion
8814.

Let P(a sec theta,b tan theta) and Q(a sec phi, b tan phi) where is the point of intersection of normals at P and Q then k is equal to

Answer»

`(a^(2)+B^(2))/(a)`
`-[(a^(2)+b^(2))/(a)]`
`(a^(2)+b^(2))/(b)`
`-[(a^(2)+b^(2))/(b)]`

ANSWER :D
Discussion
8815.

A spherical ball of salt is dissolving in water in such a manner that the rate of decrease of the volume at any instant is propotional to the surface. Prove that the radius is decreasing at a constant rate. Hint for solution : Take volume V and curve surface are S of spherical ball. Calculate by taking (dV)/(dt)alpha S.

Answer»


ANSWER :`(DR)/(DT)=K`
Discussion
8816.

For the matrix A=[{:(1,1,1),(1,2,-3),(2,-1,3):}] Show that A^3-6A^2+5A+11I=O. Hence find A^(-1)

Answer»


ANSWER :`thereforeA^(-1)=1/(11)[{:(-3,4,5),(9,-1,-4),(5,-3,-1):}]`
Discussion
8817.

Find the locus of PIf the distance of P from (3,0) is twice the distance of P from (-3,0)

Answer»


ANSWER :`X^(2)+y^(2)+10x+9=0`
Discussion
8818.

A special die is so constructed that the probabilities of throwing 1, 2, 3, 4, 5 and 6 are (1-k)/(6), (1+2k)/(6), (1-k)/(6), (1+k)/(6), (1-2k)/(6) and (1+k)/(6), respectively. If two such thrown and the probability of getting a sum equal to lies between (1)/(9) and (2)/(9), then the integral value of k is

Answer»


ANSWER :`(0)`
Discussion
8819.

Al Capone and his (n-1) friends are sitting in a circular fashion when Tintin meets him(To- tal of n people). Each of them owns a coin. First person passes 1 coin to the person sitting on his left side. The second person in turn passes 2 coins to the person sitting on the left. Third person passes 1 coin to the left, 4th passes 2 coin to his left and so on. So each person receiving 1 coin from the right has to pass 2 coins to the left. Similarly, a person receiving 2 coins from the right has to pass 1 coin to the left. If at any point of time, a person runs out of coin he is thrown out of the game. The game will terminate if at the end only 1 person is left with all the coins in his posses- sion. There might be values of n where the game may not terminate e.g. 3 persons left with 4 4 4 coins respectively. For how many different values of n from 4 to 100 does the game terminate?

Answer»

16
7
10
46

Solution :If you START observing behaviour of games starting from N=1, you can observe patternswhich you can generalize. It is easy to see that in the first round each person sitting at aneven numbered position will be thrown out of the game as he/she has 1 COIN initially,receives 1 coin from right but has to now pass both the coins to the left. ALSO observe thatthe 1st person will be always thrown out of the game. If n = 2k, after the first round k­1 willremain. If n = 2k+1, then k will remain.Case 1 :​ n is evenfor n=2k , after the first round configuration would look like3(4) 5(2) 7(2) … 2k­1(2)where a(b) denotes position a with b coins. at this point of time. Number of remainingpeople are k, if k is odd the game will not terminate because a person who looses one coinin a round will gain one coin in the next round.Case 2 :​ n is odd
for n=2k+1, after the first round configuration would look like3(3) 5(2) … `2k+1(2)`
If k is odd, the game will not terminate. If both the cases if k is even, at the end of tworounds exactly half will remain. Because a person who looses a coin will keep loosing insubsequent round.
After this elimination you again have to DEAL with cases where remaining people are odd oreven. Thus you can observe that if after the first roundpeople remain then the game willalways terminate. This can happen if initially there areorperson are there. 
Hence, the Answer is option: C)10
Discussion
8820.

If y=(sinx)^(cosx)+x^(sinx) find dy/dx.

Answer»


ANSWER :`dy/dx=(LOGX)^(cosx)[(cosx)/(x logx)-sinx LOG(logx)]+x^(sinx)[(sinx)/x+logx.cosx]`
Discussion
8821.

If int (1)/(sin x + sqrt(3) cos x)dx = A log | tan f (x) | + C then A , f(x) =

Answer»

`(1)/(2), (x)/(2) + (PI)/(6)`
`(1)/(3) , (x)/(2) + (pi)/(2)`
`(1)/(4),(pi)/(2)+ (pi)/(6)`
`(1)/(2), x + (pi)/(6)`

Answer :A
Discussion
8822.

In the figure, the area of reactangle ABCD is 100. what is the area of the square EFGH?

Answer»

256
275
309
401

Answer :D
Discussion
8823.

int(2x^3+3x^2-3)/(2x^2-x-1)dx=

Answer»

`(x^2)/(2)+2x+(5)/(6)log|2x+1|+(1)/(3)log|x-1|+c`
`(x^2)/(2)+2x+(5)/(6)log|2x+1|+(2)/(3)log|x-1|+c`
`(x^2)/(2)+2x+(1)/(6)log|2x+1|+(2)/(3)log|x-1|+c`
`(x^2)/(2)+2x+(1)/(6)log|2x+1|+(1)/(3)log|x-1|+c`

ANSWER :B
Discussion
8824.

If high voltage current is applied on the field given by the grapjh y+|y|-x-|x|=0. on which of the following curve a person can move so that the ramains safe ?

Answer»

`y=X ^(2)`
`y=sgn(-E ^(2))`
`y= log _(1//3) x`
`y=m +|x| ,mgt 3`

ANSWER :D
Discussion
8825.

find the roots x^(11)-x^7+x^4-1=0

Answer»
Discussion
8826.

Find (dy)/(dx) of the functionsy^(x)= x^(y)

Answer»


ANSWER :`(y)/(X) [(y-x LOG y)/(x-ylog x)]`
Discussion
8827.

Integration using rigonometric identities : int sin(101x)*sin^(99)x dx=...+c

Answer»

`(sin(100x)*(SINX)^(100))/(100)`
`(cos(100x)*(cosx)^(100))/(100)`
`(cos(100x)*(cosx)^(100))/(100)`
`(sin(100x)*(sinx)^(100))/(101)`

Answer :A
Discussion
8828.

What is the angle substended by an edge of regular tetrahedron at its centre?

Answer»

`cos^(-1)((-1)/(2))`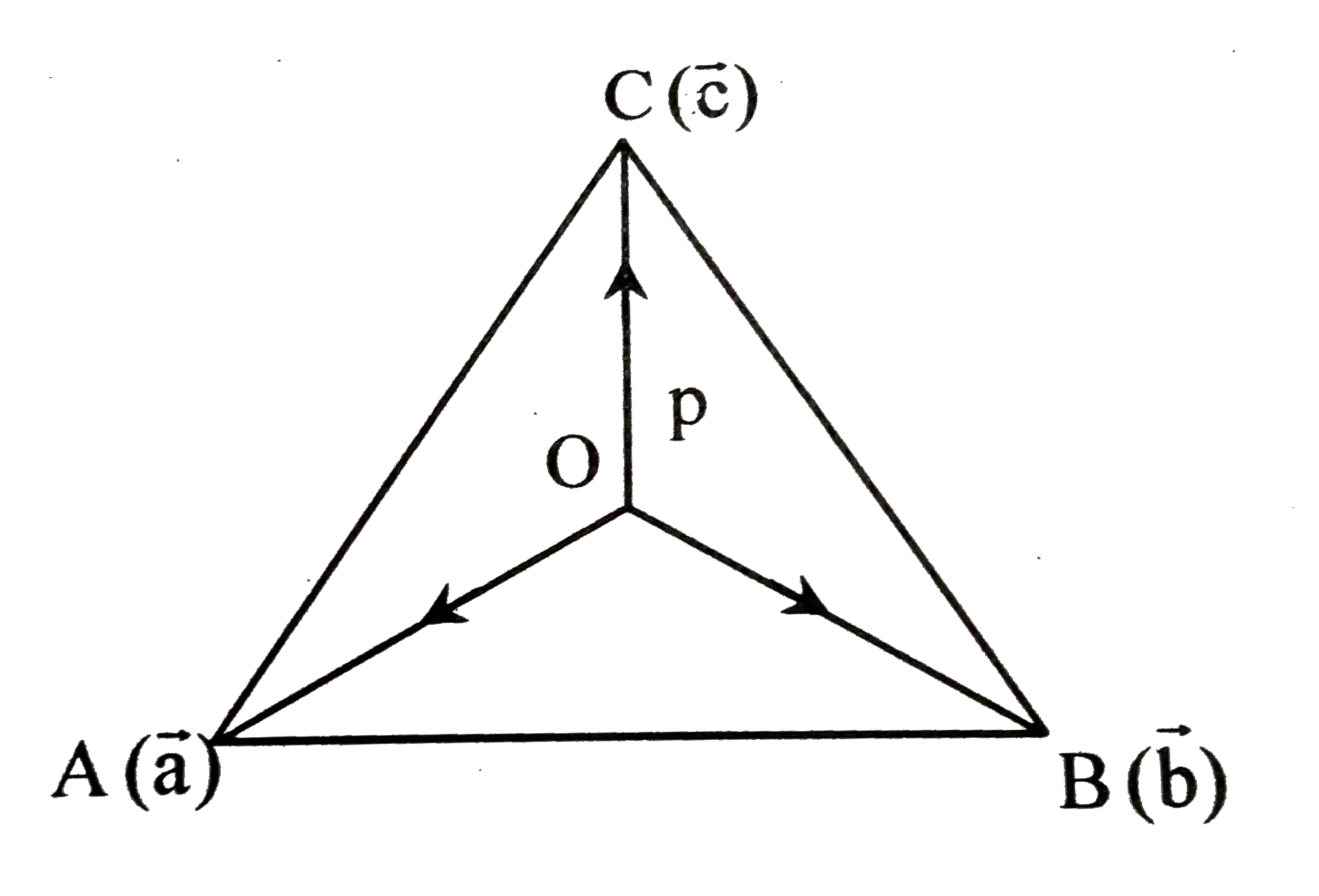
`cos^(-1)((-1)/(sqrt(2)))`
`cos^(-1)((-1)/(3))`
`cos^(-1)((-1)/(sqrt(3)))`

Solution :
`veca,vecb,vecc`
are unit vector
`veca^^vecb=vecb^^vecc=vecc^^veca=(pi)/(3)`
centre p `((veco +veca+vecb+vecc)/(4))`
Now anglebetween `VEC(AP)&vec(BP)`
`costheta=(vec(AP)*vec(BP))/(|vec(AP)||vec(BP))=(((veca+vecb+vecc)/(4)-veca)*((veca+vecb+vecc)/(4)-vecb))/(|(veca+vecb+vecc)/(4)-veca||(veca+vecb+vecc)/(4)-vecb|)`
`=((vecb+vecc-3veca)*(veca+vecc-3VECB))/(|vecb+vecc-3veca|*|veca+vecc-3vecb|)`
`=(veca*vecb+vecb*vecc-3vec(b^(2))+veca*vecc+vec(c^(2))-3vecb*c-3vec(a^(2))-3veca*vecc+9veca*vecb)/((vec(b^(2))+vec(c^(2))+9vec(a^(2))+2vecb*vecc-6veca*vecc-6veca*vecb))`
`((1)/(2)+(1)/(2)-3+(1)/(2)+1-(3)/(2)-3-(3)/(2)+(9)/(2))/(1+1+9+1-3-3)`
`=(-5+3)/(6)=-(1)/(3)`
`theta=cos^(-1)(-(1)/(3))`
Discussion
8829.

Let P and T be the subsets of X-y planedefined by fP={(x,y):x le 0,y and x^(2)+y^(2)=1} T={(x,y):xgt0,ygt0 and x^(8)+y^(8)lt1}thenP cup T is

Answer»

the voidset `PHI`
P
T
`P-T^(C )`

ANSWER :B::D
Discussion
8830.

In a Binomial distribution mean is 4 and variance is 3 find P(X ge 1).

Answer»


ANSWER :`1-((3)/(4))^(16)`
Discussion
8831.

Find the number of 4 letter words that can be formed using the letters of the word "EQUATION". begin and end with vowe

Answer»


ANSWER :1050
Discussion
8832.

Let f(x) ={{:( x+2, 0 le x lt 2),( 6-x, x ge 2):}, g(x)={{:( 1+ tan x, 0le x lt (pi) /(4)),( 3-cotx,(pi)/(4) le x lt pi ):} the numberof pointof non - differentiability ofh(x) =|f(g(x))|is

Answer»

1
2
3
4

Answer :B
Discussion
8833.

Determine the number of 8-tuples (in_(1), in_(2),…, in_(8)) such that in_(1), in_(2),.., in_(8) in (1, -1) and in_(1) 2 in_(2) + 3 in_(3) + …+ 8 in_(8) is a multiple of 3.

Answer»


ANSWER :88
Discussion
8834.

a**b = (ab)/(1) defined on Q. Inverse of 0.001 is…........

Answer»

1000000
10000
100000
1000

Answer :C
Discussion
8835.

Draw the graph of y=log_(e)(-x),-log_(e)x,y=|log_(e)x|,y=log_(e)|x| and y=|log_(e)|x|| transforming the graph of y=log_(e)x.

Answer»

SOLUTION :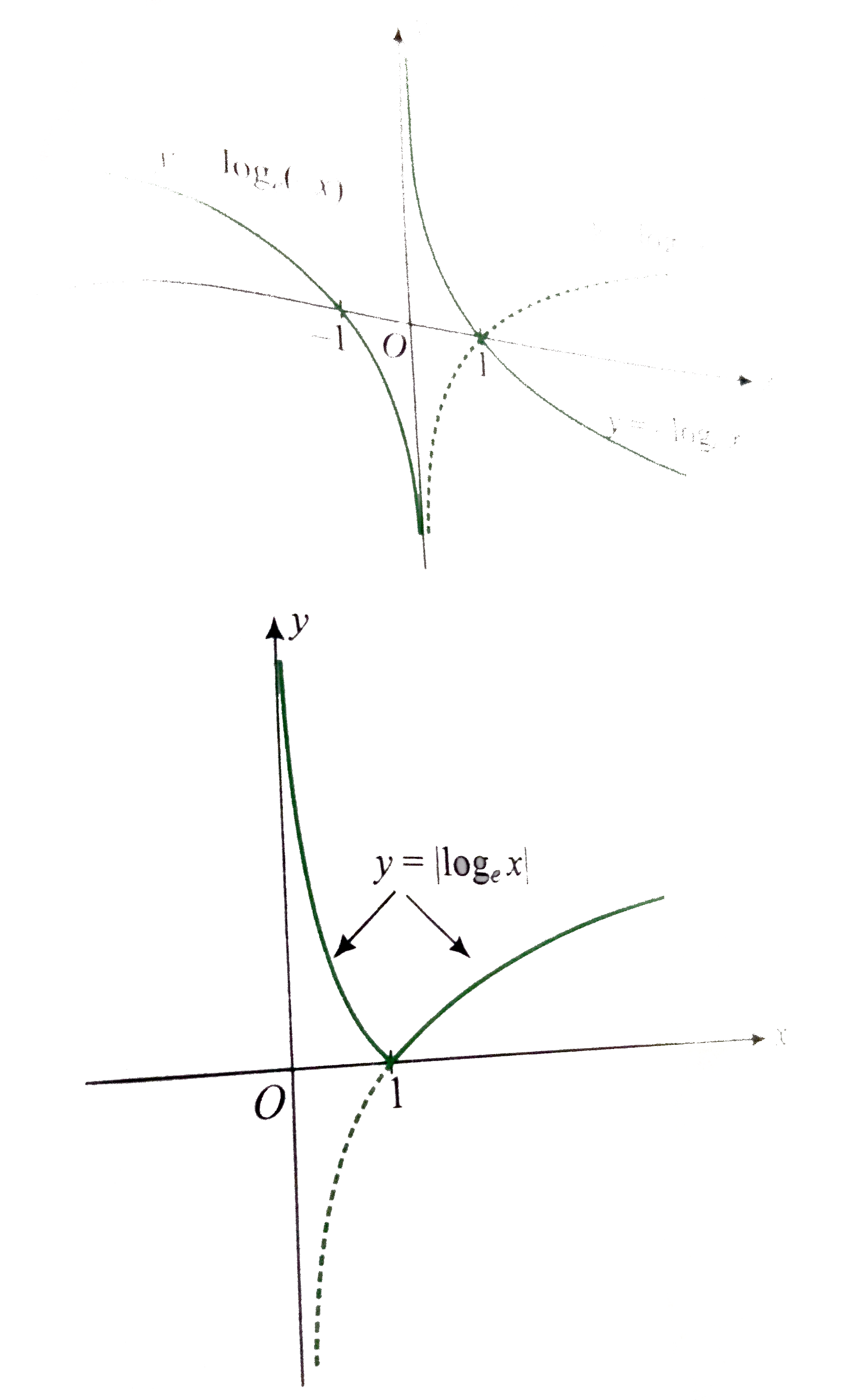
Discussion
8836.

{:(" "Lt),(n rarr oo):}(1)/(n^(6)){(n+1)^(5)+(n+2)^(5)+...+(2n)^(5)}=

Answer»

0
`21/2`
`31/2`
`32/3`

ANSWER :B
Discussion
8837.

Let A = {x in N: x is a multiple of 3 and x le 100} B ={x in N : x is a multiple of 5 and x le 100}, The number of elements of (A xx B) cap (B xx A)

Answer»

6
18
36
72

Answer :C
Discussion
8838.

bar(a) and bar(b) are unit vectors. |bar(a)+bar(b)|=sqrt(3) then the value of (3bar(a)-4bar(b)).(2bar(a)+5bar(b)) = ……………

Answer»

`-21`
21
`(21)/(2)`
`-(21)/(2)`

ANSWER :D
Discussion
8839.

intx cosec x Cotx dx =

Answer»

xcosecx - log `| TAN ""(x)/(2)| + c`
`-`xcosecx + log `| tan ""(x)/(2)| + c`
xcosecx - 2LOG `| tan ""(x)/(2)| + c`
xCotx + log `|tan ""(x)/(2)|+ c`

ANSWER :B
Discussion
8840.

If |(1,a^(2),a^(4)),(1,b^(2),b^(4)),(1,c^(2),c^(4))|=k|(1,1,1),(a,b,c),(a^(2),b^(2),c^(2))| then k is

Answer»

`(a + B) (b + c) (c + a)`
`ab + bc + AC`
` a^(2)b^(2)c^(2)`
`a^(2)+b^(2)+c^(2)`

ANSWER :A
Discussion
8841.

Integration of a binomialdifferential int(dx)/(x^(4)sqrt(1+x^(2))).

Answer»


Answer :`(sqrt(1+x^(2))(2x^(2)-1))/(3x^(3))+C.`
Discussion
8842.

If A={:[(i,i),(-i,i)] and B= [{:( 1,-1),(-1,1) :}]thenA^(8)equals

Answer»

4B
128B
`-128B `
` -64B`

ANSWER :B
Discussion
8843.

Statement-I : log(1+x+x^(2)+…)=x+(x^(2))/(2)+(x^(3))/(3)+(x^(4))/(4)+… Statement-II : 4^(th) term of log(3//2) is (-1)/(64) Statement-III: "Tan"^(2)x-(1)/(2)"Tan"^(4)x+(1)/(3)"Tan"^(6)x ………. =2log(sec x) Which of the above statements are true

Answer»

I, II are TRUE
II, III are true
I, III are true
All are true

ANSWER :B
Discussion
8844.

If P(B)= (3)/(5), P(A//B)= (1)/(2) and P(A cup B)= (4)/(5) then P(A cup B)' + P(A' cup B)=……….

Answer»

`(1)/(5)`
`(4)/(5)`
`(1)/(2)`
1

Answer :D
Discussion
8845.

For nge 2, let a_(n)=sum_(r=0)^(n)1/(C_(r)^(2)), then value of b_(n)=sum_(r=1)^(n)1/(r^(2)C_(r)^(2)) equals

Answer»

`1/(N^(2))a_(n)`
`1/(n^(2))a_(n-1)`
`a_(n)`
`a_(n)^(2)`

ANSWER :B
Discussion
8846.

Shortest distance between z-axis and the line (x-2)/(3)=(y-5)/(2)=(z+1)/(-5) is

Answer»

`1//SQRT(13)`
`11//13`
`sqrt(11)//13`
`11//sqrt(13)`

ANSWER :D
Discussion
8847.

Drawthe graph of y=sin^(-1)(2xsqrt(1-x^(2)))

Answer»

Solution :We have `y=f(X)=sin^(-1)(2xsqrt(1-x^(2)))`
Clearly, the domain of the function is [-1, 1].
LET `x=sintheta, theta in[-pi//2,pi//2]`
`rArr""theta=sin^(-1)x`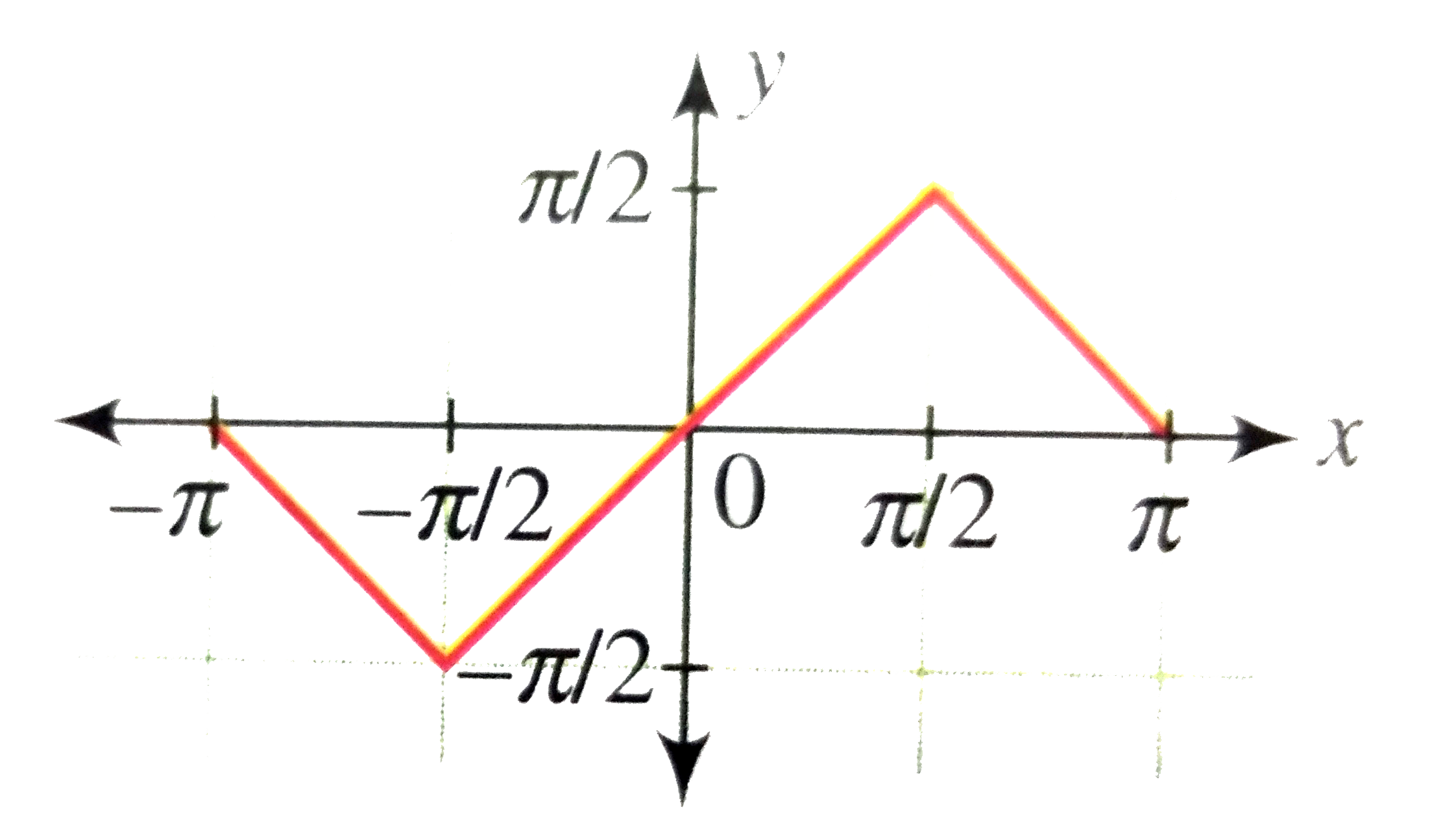

Now `sin(2xsqrt(1-x^(2)))=sin^(-1)(2 sinthetacostheta)`
`=sin^(-1)(sin2theta)`
`=sin^(-1)(sinalpha)," where "alpha in [-pi,pi]`
Now consider the GRAPH of `y=sin^(-1)(sin alpha)," where "alpha in [-pi, pi]`
From the grph,
`y=f(x)=sin^(-1)(2xsqrt(1-x^(2)))=sin^(-1)(sin alpha)`
`={{:(-alpha-pi,-pilealphalt-pi//2),(alpha, -pi//2alphalepi//2),(-alpha+pi,pi//2ltalphalepi):}`
`={{:(-2sin^(-1)x-pi,-pile2sin^(-1)xlt-pi//2),(2sin^(-1)x,-pi//2le2sin^(-1)xlepi//2),(-2sin^(-1)x+pi,pi//2lt2sin^(-1)xltpi):}`
`={{:(-2sin^(-1)x-pi,-pile2sin^(-1)xlt-pi//4),(2sin^(-1)x,-pi//pile4sin^(-1)xlepi//4),(-2sin^(-1)x+pi,pi//4ltsin^(-1)xltpi//2):}`
`={{:(-2sin^(-1)x-pi,-1lexlt-1/sqrt2),(2sin^(-1)x,-1/sqrt2lexle1/sqrt2),(-2sin^(-1)x+pi,-1/sqrt2lexle1):}`
`={{:(-2/sqrt(1-x^(2)),-1ltxlt-1/sqrt(2)),(2/sqrt(1-x^(2)),-1ltxlt-1/sqrt(2)),(-2/sqrt(1-x^(2)),-1ltxlt1):}`
Clearly, y = f(x) is non-differentiable at `x=+-1/sqrt2`
y=f(x) inreases for `x in (-1/sqrt2,-1/sqrt2)` and decreases for `x in (-1,-1/sqrt2)cup(1/sqrt2,1)`
For f(x) `= -2 sin^(-1)x-pi`
`f(-1)=-2sin^(-1)(-1)-pi=0,f(-1/sqrt2)=-2(-pi/4)-pi=-pi/2`
Thus, `sin^(-1)(2xsqrt(1-x^(2)))` decreases from 0 to `-pi/2` when x increases from -1 to `-1/sqrt2`.
For `f(x)=2sin^(-2)x`
`f(-1/sqrt2)=2(-pi/4)=-pi/2`
`f(1/sqrt2)=2(pi/4)=pi/2`
Thus, `sin^(-1)(2xsqrt(1-x^(2)))" increases from "=pi/2"to"pi/2" when x in creases from "-1/sqrt2"to"1/sqrt2`
For `f(x)=-2sin^(-1)x+pi`
`f(1/sqrt2)=-2(pi/4)+pi=pi/2,f(1)=-2sin^(-1)(1)+pi=0`
Thus, `sin^(-1)(2xsqrt(1-x^(2)))" decreases from "pi/2"to"0`
When x increases from `1/sqrt2"to1`.
From this INFORMATION, we can DRAW the graph of `sin^(-1)(2xsqrt(1-x^(2)))` as shown in the adjecnt figure.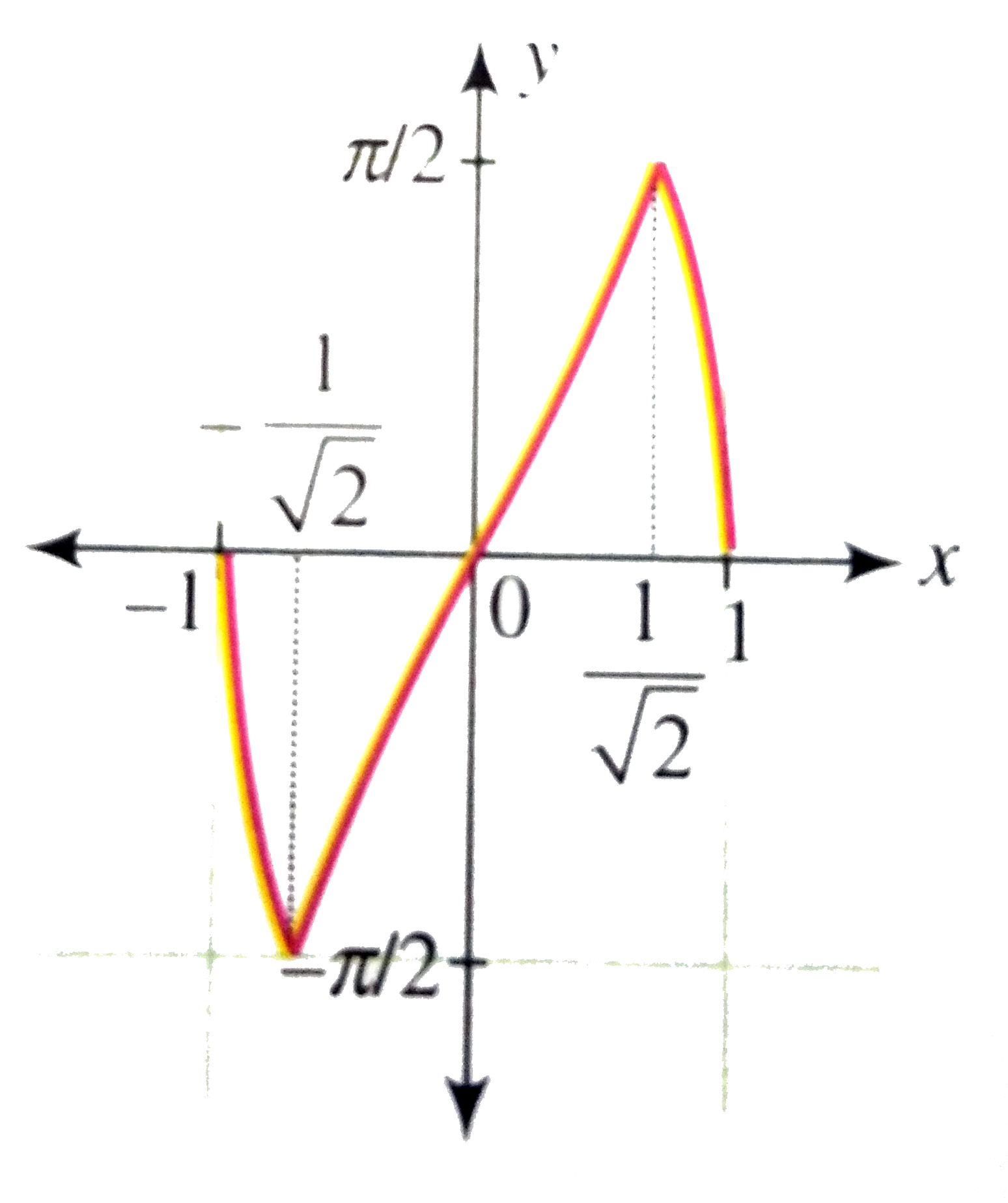
Discussion
8848.

If a line makes angles 90^@, 135^@, 45^@ with the x, y and z- axes respectively, find its direction cosines.

Answer»


ANSWER :0,`-(1)/(SQRT2),(1)/(sqrt2)`
Discussion
8849.

A function f:RtoR is such that f(x+y)=f(x).f(y) for all x.y inR and f(x)ne0 for all x inR. If f'(0)=2 then f'(x) is equal to

Answer»

`f(X)`
`-f(x)`
`2f(x)`
`4F(x)`

ANSWER :C
Discussion
8850.

If alpha, beta and gamma are the roots of the equation x^(3)+px^(2)+qx+r=0 , then the coefficient of x in the cubic equation whose roots are alpha(beta+gamma), beta(gamma+alpha) and gamma(alpha+beta) is

Answer»

2q
`Q^(2)+PR`
`p^(2)-qr`
`r(pq-r)`

ANSWER :B
Discussion