InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 8901. |
Number of solutions of the equation sin^4x-cos^2xsinx+2sin^2x+sinx=0in0lt=xlt=3piis_____ |
| Answer» Answer :D | |
| 8902. |
Consider the circle x^(2)+(y-1)^(2)=9, (x-1)^(2)+y^(2)=25. They are such that |
|
Answer» these CIRCLES TOUCH each other |
|
| 8903. |
A problem in mathematics is given to three students A, B, C and their respective probability of solving the problem is (1)/(2), (1)/(3) and (1)/(4). Probability that the problem is solved is ……… |
|
Answer» `(3)/(4)` |
|
| 8904. |
A problem in mathematics is given to three students A, B, C and their respective probability of solving the problem is (1)/(2),(1)/(3) and (1)/(4) . Probability that the problem is solved is ........ |
|
Answer» `(1)/(2)` |
|
| 8905. |
Let U (x) and V(x)be two differentiablefunction. Given(U(x))/(V(x))=7,if(U'(x))/(V'(x))=pand[(U(x))/(V(x))]=q then the value of(p+q)/(p-q)is_ |
|
Answer» |
|
| 8906. |
Evaluate the following integrals intlog(1+x^(2))dx |
|
Answer» |
|
| 8907. |
Evaluate the following integrals int cos (log x) dx |
|
Answer» |
|
| 8908. |
If I_(n)= int (log x)^(n)dx then I_(n)+nI_(n-1)= |
|
Answer» `x("l N x")^(n- 1)` |
|
| 8909. |
Express with rational denominator(x+sqrt(-1))^2/(x-sqrt(-1))-((x-sqrt(-1^2)))/(x+sqrt(-1)) |
|
Answer» SOLUTION :`(x+sqrt(-1))^2/(x-sqrt(-1))-((x-sqrt(-1^2)))/(x+sqrt(-1))` `((x+i)^2)/(x-i)-(x-i)^2/(x=i)=((x+i)^3-(x-i)^3)/((x-i)(x+i))` `=(2(3x^2I+i^3))/(x^2-i^2)=(2(3x^2i-i))/(x^2+1)` `=(2i(3x^2-1))/(x^2+1)` |
|
| 8910. |
For the function f(x)=int_(0)^(x^(2))(-t^(2)/4)(4-t)dt |
|
Answer» LOCAL maximum OCCURS at x = 2 |
|
| 8911. |
Find the second order derivatives of the following functions: 3 sin 4x-4sin^(3) 4x |
|
Answer» |
|
| 8912. |
In Z the set of all integers, the inverse of -7 w.r.t. '**' defined by a**b=a+b+7 for all a, bin Z is |
| Answer» ANSWER :D | |
| 8913. |
If tan^(-1) x + tan^(-1) y + tan ^(-1) z = (pi)/(2) , then value of xy + yz + zxa) -1 b) 1 c) 0 d) None of these |
|
Answer» `-1` |
|
| 8914. |
Integrate the rational functions 1/((e^(x)-1)) [Hint : Put e^(x) = t] |
|
Answer» |
|
| 8915. |
Let A={x_(1),x_(2),x_(3)....,x_(7)},B={y_(1)y_(2)y_(3)}. The total number of functions f:AtoB that are onto and ther are exactly three elements x in A such that f(x)=y_(2), is equal to |
| Answer» | |
| 8916. |
Find the approximate change in the volume V of a cube of side x metres caused by increasing the side by 1%. |
|
Answer» |
|
| 8917. |
If the lines (x-1)/(-3)=(y-2)/(2k)=(z-3)/(2) and (x-1)/(3k)=(y-1)/(1)=(z-6)/(-5) are perpendicular, find the value of k. |
|
Answer» |
|
| 8918. |
The tagents at any point P of the circle x^(2)+y^(2)=16 meets the tangents at a fixed point A at T. Point is joined to B,the other end of the diameter, through, A. The sum of focal distance of any point on the curce is |
|
Answer» 12 The EQUATION of AP is `y=(sin theta)/(cos theta-1)(x-4)""(2)` 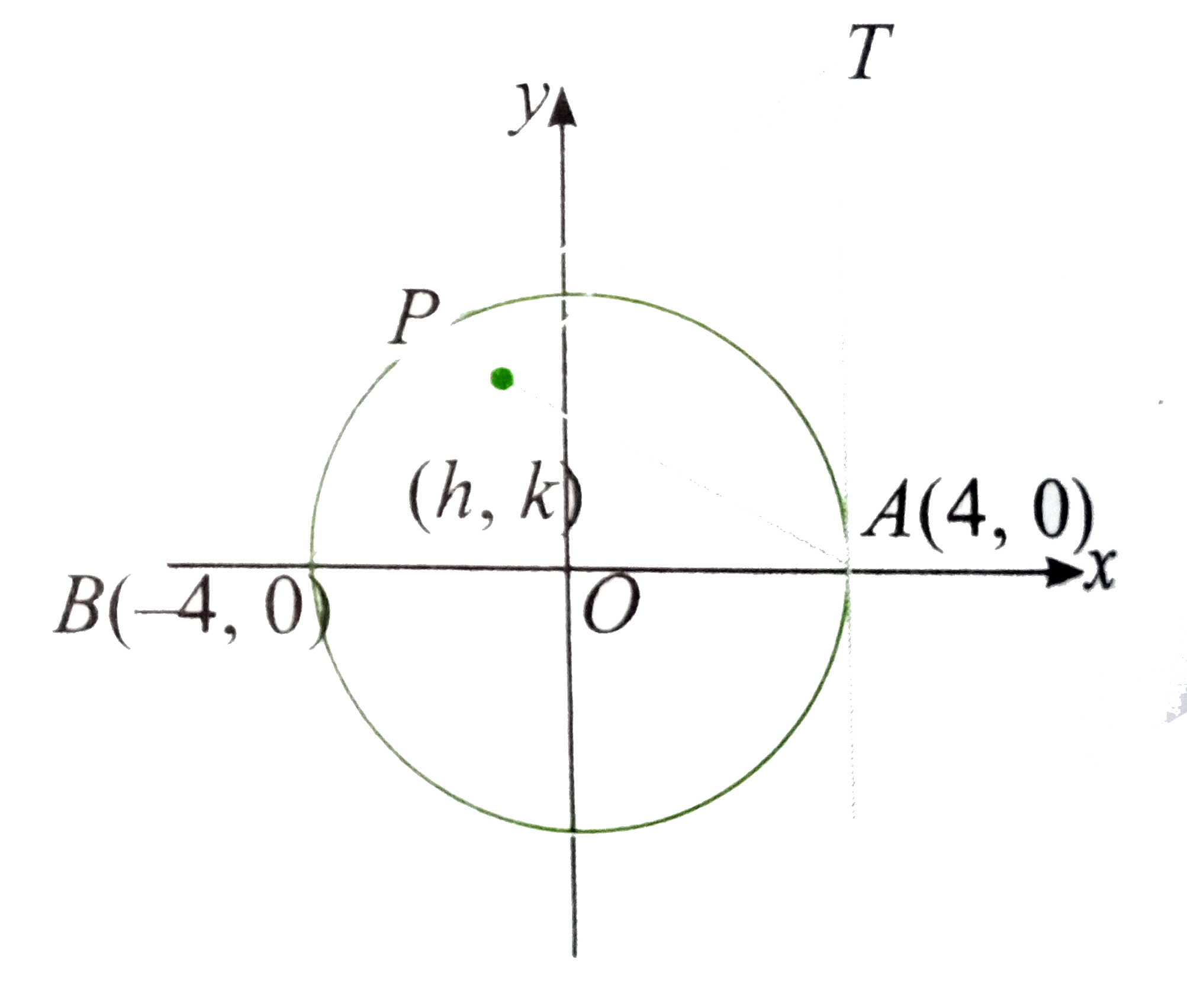 From (1), the COORDINATES of the point T are given by `(4,(4(1-costheta))/(sin theta))` The equation of BT is `y=(1-cos theta)/(2 sin theta)(x+4)""(3)` Let (h,K) be the point of intersection of the lines (2), and (3). Then we have `k^(2)=-(1)/(2)(h^(2)-16)` or `(h^(2))/(16)+(y^(2))/(8)=1` Therefore, the locus of (h,k) is `(x^(2))/(16)+(y^(2))/(8)=1` Which is an ellipse with eccehntrically `e=1//sqrt(2)` Sumof focal distance of any points is 2a=8 Considering the circle `x^(2)+y^(2)=a^(2)`, we find the that the eccentricity of the ellipse is `1sqrt(2)` which is contant and does not CHANGE by changing the radius of the circle |
|
| 8919. |
The tagents at any point P of the circle x^(2)+y^(2)=16 meets the tangents at a fixed point A at T. Point is joined to B,the other end of the diameter, through, A. Which of the following does not change by changing the radius of the circle ? |
|
Answer» Coordinartes of foci The equation of AP is `y=(sin theta)/(cos theta-1)(x-4)""(2)` 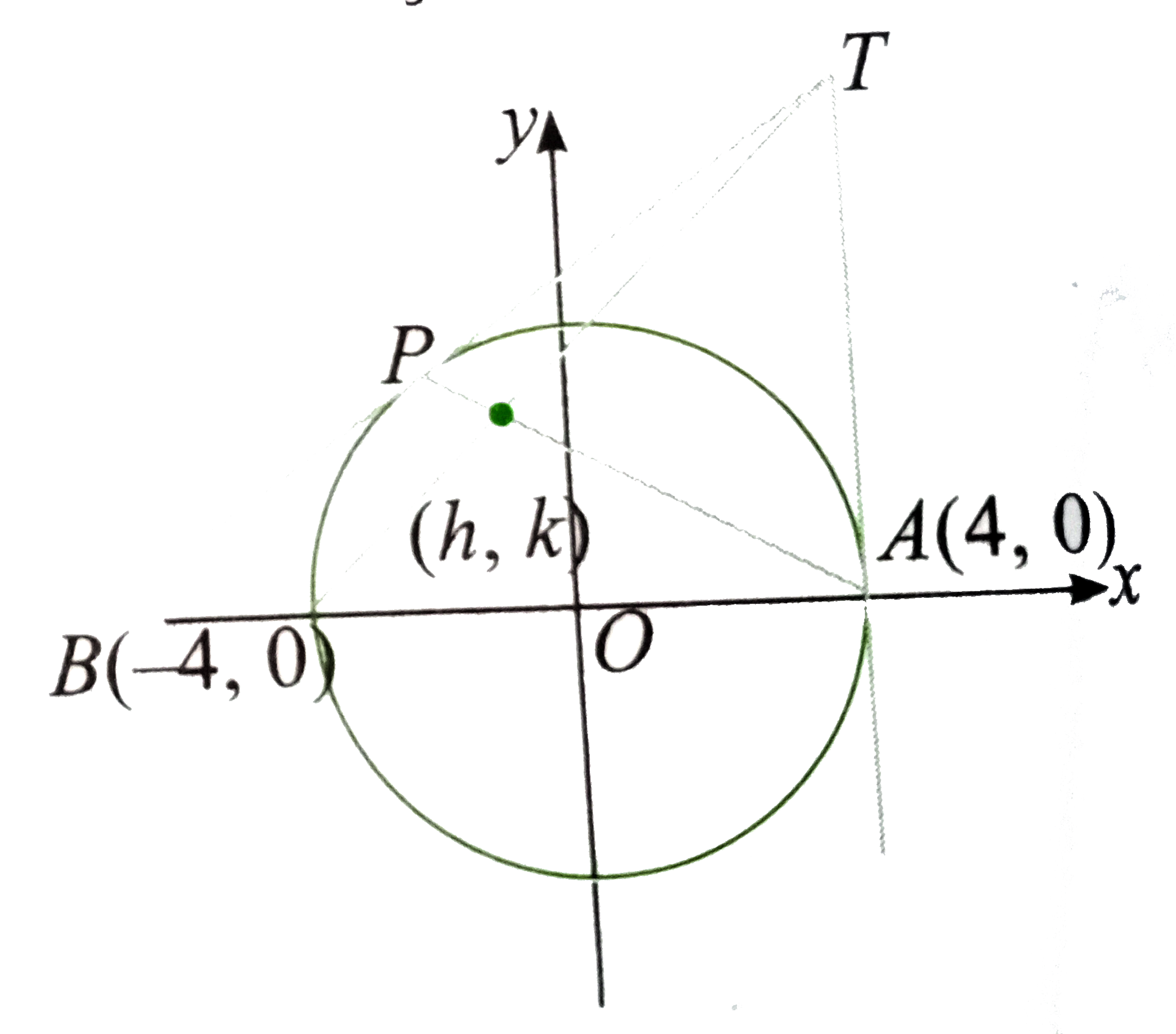 From (1), the coordinates of the point T are given by `(4,(4(1-costheta))/(sin theta))` The equation of BT is `y=(1-cos theta)/(2 sin theta)(x+4)""(3)` LET (h,k) be the point of intersection of the lines (2), and (3). Then we have `k^(2)=-(1)/(2)(h^(2)-16)` or `(h^(2))/(16)+(y^(2))/(8)=1` Therefore, the locus of (h,k) is `(x^(2))/(16)+(y^(2))/(8)=1` Which is an ELLIPSE with eccehntrically `e=1//sqrt(2)` Sumof focal distance of any points is 2a=8 Considering the circle `x^(2)+y^(2)=a^(2)`, we find the that the eccentricity of the ellipse is `1sqrt(2)` which is contant and does not change by changing the radius of the circle |
|
| 8920. |
The tagents at any point P of the circle x^(2)+y^(2)=16 meets the tangents at a fixed point A at T. Point is joined to B,the other end of the diameter, through, A. The locus of the intersection of AO and BT is a conic whosee eccentricity is |
|
Answer» `1//2` The equation of AP is `y=(sin theta)/(cos theta-1)(x-4)""(2)`  From (1), the coordinates of the point T are given by `(4,(4(1-costheta))/(sin theta))` The equation of BT is `y=(1-cos theta)/(2 sin theta)(x+4)""(3)` Let (h,k) be the point of intersection of the lines (2), and (3). Then we have `k^(2)=-(1)/(2)(h^(2)-16)` or `(h^(2))/(16)+(y^(2))/(8)=1` Therefore, the locus of (h,k) is `(x^(2))/(16)+(y^(2))/(8)=1` Which is an ellipse with eccehntrically `e=1//sqrt(2)` Sumof FOCAL distance of any points is 2a=8 Considering the circle `x^(2)+y^(2)=a^(2)`, we find the that the ECCENTRICITY of the ellipse is `1sqrt(2)` which is contant and does not CHANGE by CHANGING the radius of the circle |
|
| 8921. |
Find the values of x and y from the following equation , 2[{:(x,5),(7,y-3):}]+[{:(3,-4),(1,2):}]=[{:(7,6),(15,14):}]. |
|
Answer» |
|
| 8922. |
Let f(x) = |(cosx,sinx,cosx),(cos2x,sin2x,2cos2x),(cos3x,sin3x,3cos3x)| then the value of f'(pi/2) is : |
|
Answer» 0 `Delta_(1) = -4: Delta_(2) = 0` and `Delta_(3) = 8]` |
|
| 8923. |
The mean of 20 observations is 15. On Checking it was found that two observations were wrongly copied as 3 3 and 6. If wrong observations are replaced by correct values 8 and 4, then the correct means is |
|
Answer» 15 |
|
| 8924. |
If sum of n terms of a sequence is given by S _(n) = 2n ^(2) - 4n, find its 50^(th) term. |
|
Answer» |
|
| 8925. |
If bar(x)=(-1,4,-2),bar(y)=(-4,16,-8) then |bar(x)+bar(y)|…………|bar(x)|+|bar(y)| |
| Answer» ANSWER :A | |
| 8926. |
Differentiate the functions with respect to x in Exerecises 1 to 8. sin (ax+b) |
|
Answer» |
|
| 8927. |
There is an error of pm0.04 cm in the measurement of the diameter of a sphere. When the radius is 10 cm, the percentage error in the volume of the sphere is |
|
Answer» `pm1.2` |
|
| 8928. |
If p, q and r are three logical statements then the truth value of the statement (p^^~q)vv(qrarr r), where p is true,is |
|
Answer» TRUE if q is true |
|
| 8929. |
find the following definite trigonometric integral as limit of sums. overset(pi)underset(0) int sinx dx |
|
Answer» |
|
| 8930. |
Value of the Delta=|{:(,a^(3)-x,a^(4)-x,a^(5)-x),(,a^(5)-x,a^(6)-x,a^(7)-x),(,a^(7)-a,a^(8)-x,a^(9)-x):}| then the value of Delta_(1)-Delta_(2) is |
|
Answer» 0 |
|
| 8931. |
A firm can produce three types of cloth say 'A', 'B' and 'C'.Three kinds of wool are required for it, say red wool, green wool and blue wool.One unit length of type 'A' cloth needs 2 yards of red wool and 3 yards of blue wool, one unit length of type 'B' cloth needs 3 yards of red wool, 2 yards of gren wool and 2 yards of blue wool, one unit length of type 'C' cloth needs 5 yards of green wool and 4 yards of blue wool.The firm has only a stock of 8 yards of red wool, 10 yards of green wool and 15 yards of blue wool.It is assumed that the income obtained from one unit of type 'A' cloth is ₹ 3, for type 'B' cloth is ₹ 5 and for type 'C' cloth is ₹ 4.Formulate the problem as a LPP so as to maximize the profit of the firm by using the available materials. |
|
Answer» <P> `2x + 3y le 8, 2y+ 5zle 10, 2y + 4z le 15, x GE 0, y ge 0, z ge 0`. |
|
| 8932. |
If 1 , omega , omega^(2) are the cube roots of unity, then prove that 1/(2 + omega) - 1/(1+2 omega) = 1/(1 + omega) . |
| Answer» | |
| 8933. |
If the coefficient of x^(5) in the expansion of (ax^(2)+(1)/(bx))^(13) is equal to the coefficient of x^(-5) in the expansion of (ax-(1)/(bx^(2)))^(13), then ab = |
| Answer» Answer :A | |
| 8934. |
Find the equation of the circle with centre C and redius r where. C= (1,7) , r =5/2 |
|
Answer» |
|
| 8935. |
If f(x )=0hasarepreatedrootalphathenanotherequationhavingalphaas rootis |
|
Answer» `f(2X )=0` |
|
| 8936. |
If P(A) = 1/2, P(B) = 7/12 and P(not A or not B) = 1/4, then A and B are independent events. |
|
Answer» |
|
| 8937. |
If a, b and c are unit vectors then abs(a-b)^(2)+abs(b-c)^(2)+abs(c-a)^(2) does not exceed. |
|
Answer» 4 |
|
| 8938. |
p : If end digit of an integer is 5 then end digit of its square is also 5. Statement p is same as the |
|
Answer» If end DIGIT of SQUARE of an integer is not 5, then. end of digit of integer is not 5 |
|
| 8939. |
Find the number of natural numbers less than 10^7 which have exactly 77 divisors. |
|
Answer» |
|
| 8940. |
Evaluate the following integrals (vi) int_(0)^(1) (1)/(sqrt(x+1)+sqrt(x))dx |
|
Answer» |
|
| 8941. |
If the system of homogeneous equations (a-1)x+(a+2)y+az=0, (a+1)x+ay+(a+2)z=0and ax+(a+1)y +(a-1)z=0has a non -tivial solution, then find the value of a . |
|
Answer» |
|
| 8942. |
If int (1)/((x + 100) sqrt(x + 99)) dx = f (x) + c then f(x) = |
|
Answer» `2(x + 100)^(1//2)` |
|
| 8943. |
if has set of all valuesof theparameter 'a' for which the function f(x) = sin 2x -8 (a+1) sin x + (4a^(2) +8a -14) x increases for allx in R and hasno critical points for all x in R" is " (-oo , -m -sqrt(n))uu (sqrt(n) ,oo) then (m^(2) +n^(2)) is (where m,n are prime numbers): |
|
Answer» |
|
| 8944. |
Prove that f(x)=5x-3 is continuous at x=0 |
| Answer» | |
| 8945. |
Statement I The circle x^(2) + y^(2) - 6x - 4y - 7 = 0 touches y-axis Statement II The circle x^(2) + y^(2) + 6x + 4y - 7 = 0 touches x-axis Which of the following is a correct statement ? |
|
Answer» Both I and II are TRUE |
|
| 8946. |
ABCDEF is a regular hexagone. AB+AC+AD+AE+AF=lambda AD then lambda = …………. |
|
Answer» 0 |
|
| 8947. |
If |z,|=1,|z_(2)|=2,|z_3|=3 and |9z_1z_2+4z_1z_3+z_2z_3|=12, then the value of |z_1+z_2+z_3| is |
|
Answer» 3 |
|
| 8948. |
int sqrt((cos x - cos^(3) x)/(1 -cos^(3) x))dx = |
|
Answer» `(-2)/(3) sin^(-1) [ (cos X)^(3//2)] `+ C |
|
| 8949. |
Find the locus of the point whose polars with respect to the circles x^(2)+y^(2)-4x-4y-8=0 and x^(2)+y^(2)-2x+6y-2=0 are mutually perpendicular. |
|
Answer» |
|
| 8950. |
Find the equation of parabola whose Vertex is (2,3) latus rectum is 8 and axis is parallel to x-axis |
|
Answer» |
|