Explore topic-wise InterviewSolutions in .

This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.

9451.

Let P_1=I=[{:(1,,0,,0),(0,,1,,0),(0,,0,,1):}],P_2=[{:(1,,0,,0),(0,,0,,1),(0,,1,,0):}] P_3=[{:(0,,1,,0),(1,,0,,0),(0,,0,,1):}],P_4=[{:(0,,1,,0),(0,,0,,1),(1,,0,,0):}] P_5=[{:(0,,0,,1),(1,,0,,0),(0,,1,,0):}],P_6=[{:(0,,0,,1),(0,,1,,0),(1,,0,,0):}] and X=sum_(k=1)^(6)P_(K)[{:(2,,1,,3),(1,,0,,2),(3,,2,,1):}]P_(K)^(T) Where , P_(K)^(T)denotes the transpose of the matrix P_(X). then which of the following option is/are correct ?

Answer»

X is a symmertic matrix
The SUM of diagonal entries of X is 18
`X-30 I` is an invertible matrix
If`X[{:(1),(1),(1):}]=alpha[{:(1),(1),(1):}],then" "alpha=30`

Solution :Given matrices,
`P_(1) = I = [{:(,1,0,0),(,0,1,0),(,0,0,1):}],P_(2)[{:(,1,0,0),(,0,0,1),(,0,1,0):}], P_(3)[{:(,0,1,0),(,1,0,0),(,0,0,1):}]`
`P_(4)=[{:(,0,1,0),(,0,0,1),(,1,0,0):}],P_(5)=[{:(,0,0,1),(,0,0,1),(,0,1,0):}], P_(6)=[{:(,0,0,1),(,0,1,0),(,0,1,0):}]`
and `X = underset(k-1)overset(6)sumP_(k) [{:(,2,1,3),(,1,0,2),(,3,2,1):}] P_(K)^(T)`
`because P_(1)^(T) = P_(1),P_(2)^(T)= P_(2),P_(3)^(T) = P_(3), P_(4)^(T) = P_(5), P_(5)^(T) = P_(4)` and
`P_(6)^(T) = P_(6)` and Let Q`= [{:(,2,1,3),(,1,0,2),(,3,2,1):}] ANDBECAUSE Q^(T) = Q`
Now,`X= (P_(1)QP_(1)^(T)) + (P_(2)QP_(2)^(T))^(T) + (P_(3)QP_(3)^(T)) + (P_(4)QP_(4)^(T))+(P_(5)QP_(5)^(T))+(P_(6)QP_(6)^(T))`
So, `X^(T) = (P_(1)QP_(1)^(T))^(T) + (P_(2)QP_(2)^(T))^(T)+(P_(3)QP_(3)^(T))^(T) + (P_(4)QP_(4)^(T))^(T) + (P_(5)QP_(5)^(T))^(T)+(P_(6)QP_(6)^(T))^(T)`
`P_(1)QP_(1)^(T) + P_(2)QP_(2)^(T)+P_(3)QP_(3)^(T) + P_(4)QP_(4)^(T) + P_(5)QP_(5)^(T)+P_(6)QP_(6)^(T)`
`[because(ABC)^(T) = C^(T)B^(T)A^(T) and (A^(T))^(T) = A and Q^(T) = Q]`
`rArr X^(T) = X`
`rArr` X is a symmetric matrix.
The sum ofdiagonal entries of `X = Tr(x)`
`=sum_(i=1)^(6) T_(R)(P_(i)QP_(i)^(T))`
`= sum_(i-1)^(6) T_(r)(QP_(i)^(T)P_(i))""[becauseT_(r)(ABC) = T_(r)(BCA)]`
`= sum_(i=l)^(6) T_(r)(Ql) ""[because P_(i)`'s "are othogonal matrices"]`
`=sum_(i=1)^(6) T_(r)(Q)= 6T_(r)(Q)= 6xx3 = 18`
`Now Let `R= [{:(,1),(,1),(,1):}]`, then
`XR = sum_(k=1)^(6) (P_(k)QP_(k)^(T)) R = sum_(k=1)^(6) (P_(k) QP_(k)^(T)R)`
`= sum_(k=1)^(6)(P_(k) QR)""[becauseP_(k)^(T)R = R]`
`= sum_(k=1)^(6) P_(k)[{:(6),(3),(6):}] = sum_(k=1)^(6) P_(k) [{:(6),(3),(6):}] = [{:(2,2,2),(2,2,2),(2,2,2):}][{:(6),(3),(6):}]`
`rArr XR = [{:(30),(30),(30):}]rArr XR = 30 R rArr X [{:(1),(1),(1):}]= 30[{:(1),(1),(1):}]`
`rArr (X-30I0 R = 0 rArr |X-30I|=0`
So, `(X - 30I)` is notinvertible and value of `alpha = 30`.
Hence, options (a),(b) and (c) are correct.
Discussion
9452.

If a _(n+1)=sqrt((1)/(2)(1+a_(n)))then cos((sqrt(1-a_(0)^(2)))/(a_(1)a_(2)a_(3)..."to"oo))=

Answer»

1
`-1`
`a_(0)`
`1//a_(0)`

ANSWER :C
Discussion
9453.

omega is the cube root of 1 and omega ne 1. Now r_(1), r_(2) and r_(3) are the number obtained whiletossing dice thrice. Then ………… is the probability for omega^(r^(1)) +omega^(r^(2))+omega^(r^(3))=0

Answer»

`(1)/(18)`
`(1)/(9)`
`(2)/(9)`
`(3)/(36)`

Answer :C
Discussion
9454.

If a vector vec( r ) has magnitude 14 and direction ratios 2, 3, -6. Then find the direction cosines and components of vec( r ), given that bar( r ) makes an acute angle with X - axis.

Answer»


ANSWER :`=4hati+6hatj-12hatk`
Discussion
9455.

Find adjoint of each of the matrices[{:(0,1,2),(1,2,3),(3,1,1):}]

Answer»


ANSWER :`[{:((1)/(2),-(1)/(2),(1)/(2)),(-4,3,1),((5)/(2),-(3)/(2),(1)/(2)):}]`
Discussion
9456.

For the synthesis of ammonia by the reaction N_(2) + 3NH_(2) hArr 2NH_(3) in the haber's process, the attainment of equilibrium is correctly predicted by the curve :-

Answer»




ANSWER :A
Discussion
9457.

Thepolynomialequationof thelowestdegreehavingroots1 , sqrt(3)iis

Answer»

`x^3 +x^2 +3X +3=0`
`x^3 -x^2 +3x-3=0`
`x^3+x^2 -3x -3=0`
`x^2 -(1+sqrt(3)i)x+sqrt(3)i =0`

ANSWER :B
Discussion
9458.

There are 3 works. One is of 3 volumes and one is of 4 volumes and one is of exactly one volume. If the books are placed in a random order on a shelf, the probability that all the volumes of the same work are together is

Answer»

`1/70`
`3/140`
`1/65`
`3/130`

ANSWER :B
Discussion
9459.

Show that addition, subtraction and multiplication are binary operations on R, but division is not a binary opertion on R. Further, show that division is binary opertion on the set R, of nonzero real numbers.

Answer»


ANSWER :On R
Discussion
9460.

Let A={1,2,3,4,5} and a relation on it is R={(x,y)//x,y in A" and "x+y=5} then R is

Answer»

not REFLEXIVE, not SYMMETRIC but transitive
not reflexive, not transitive but symmetric
not reflexive, not symmetric, not transitive
EQUIVALENCE

ANSWER :B
Discussion
9461.

If x = cis theta , then find the value of [x^(6) + 1/x^(6)].

Answer»


ANSWER :2cos6 `THETA`
Discussion
9462.

A and B are events such that P(A')= 0.3, P(B) = 0.4and P(A cap B') = 0.5then P[B | (A cup B')] =…………

Answer»

`(1)/(2)`
`(1)/(3)`
`(1)/(4)`
1

Answer :C
Discussion
9463.

A variable tangent to the ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2))=1 makes intercepts on both the axes. The locus of the middle point of the portion of the tangent between the coordinate axes is

Answer»

`(X^(2))/(b^(2))+(y^(2))/(a^(2))=1`
`(a^(2))/(x^(2))+(b^(2))/(y^(2))=1`
`b^(2)x^(2)+a^(2)y^(2)=4`
`(a^(2))/(x^(2))+(b^(2))/(y^(2))=4`

ANSWER :D
Discussion
9464.

Lt_(ntooo)[(1)/(sqrt(n^(2)-1^(2)))+(1)/(sqrt(n^(2)-2^(2)))+(1)/(sqrt((2n-1)))]=

Answer»

`PI`
`2PI`
`pi/2`
`pi/4`

ANSWER :C
Discussion
9465.

All the values of m for which both roots of the equation x^(2)-2mx+m^(2)-1=0 are greater than -2 but less than 4, lie in the interval

Answer»

`-2 LT m lt 0`
` m GT 3`
`-1 lt m lt 3`
`1 lt m lt 4`

ANSWER :C
Discussion
9466.

If1 , omega , omega^(2) are the cube roots of unity , then the roots of (x - 1)^(3) + 8 = 0 are

Answer»

`1 , OMEGA , omega^(2)`
`-1 , 1 - 2OMEGA , 1 - 2omega^(2)`
`1 , 2 - omega , 2 - omega^(2)`
`1 , 2 + omega , 2 + omega^(2)`

ANSWER :B
Discussion
9467.

(1)/(2)((1)/(5)+(1)/(7))-(1)/(4)((1)/(5^(2))+(1)/(7^(2)))+(1)/(6)((1)/(5^(3))+(1)/(7^(3)))-….oo=

Answer»

`(1)/(2)log_(E )(5//7)`
`(1)/(2)log_(e )(47//35)`
`log_(e )(47//35)`
`log_(e )(35//47)`

Answer :B
Discussion
9468.

Evaluate the following integrals (ii) int_(0)^(pi) x sin^(5) x cos^(6) x dx

Answer»


ANSWER :`(8pi)/(693)`
Discussion
9469.

Find int sec^(2) xcosec^(2) xdx

Answer»


ANSWER :TAN X - COT x + C
Discussion
9470.

The ordinate of the centroid of the triangle formed by conormal points on the parabola y^(2)=4ax is

Answer»

4
0
2
1

Answer :B
Discussion
9471.

Evaluate the definite integrals int_(2)^(3)(xdx)/(x^(2)+1)

Answer»


ANSWER :`1/2log2`
Discussion
9472.

Find the ratio in which the plane 2x-3y+6z=5 divides the line joining (2, 3, -1), (-1, 4,1).

Answer»

(5,2,0)
(5,4, – 4)
(-3,-1,-6)
(10, – 15, 12)

Answer :B
Discussion
9473.

Solve 1+sin2x=(sin3x-cos3x)^(2)

Answer»


ANSWER :`(NPI)/(4);(npi)/(2)+(pi)/(4),N INZ`
Discussion
9474.

Find the middle term(s) in the expansionof n in N (a^(3)+(2)/(b))^(4n)

Answer»


SOLUTION :N/A
Discussion
9475.

Draw the graph of y = (sin x)/(x).

Answer»

SOLUTION :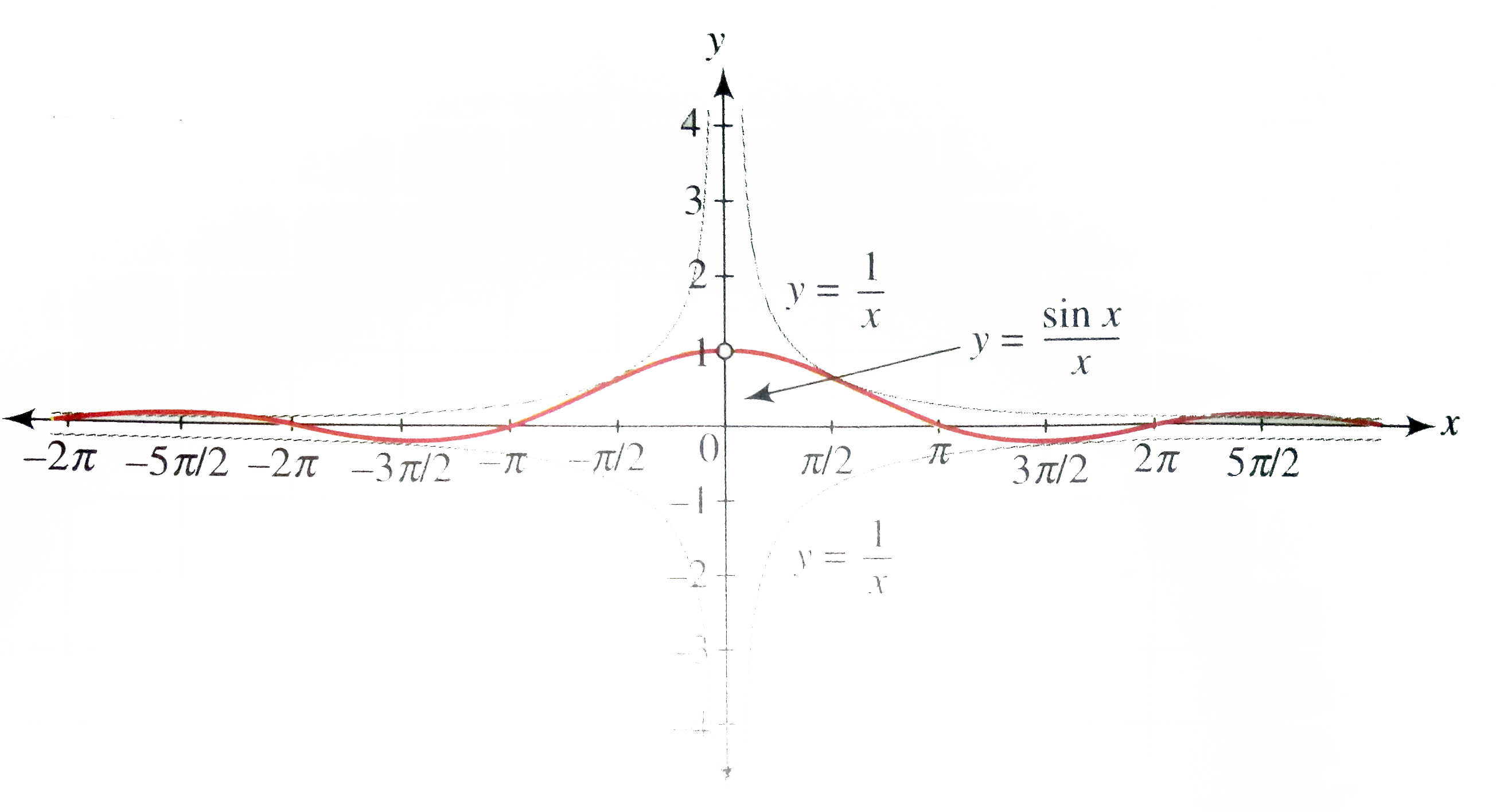
Discussion
9476.

If(1 + I sqrt(3))/(2)isa rootof theequationx^4-x^3 +x-1=0thenitsrealrootsare

Answer»

`1,1`
`-1,-1`
`1,2`
`1,-1`

ANSWER :D
Discussion
9477.

There are 10 stations enroute. A train has to be stopped at 3 of them. Let N be the no of ways is which the train can be stopped if atleast two of the stopping stations are consecutive. Find N.

Answer»


ANSWER :64
Discussion
9478.

If A and B are two matrices of the order 3xxmand3xxn , respectively , and m=n , then the order of matrix (5A-2B) is ……….

Answer»

`mxx3`
`3xx3`
`mxxn`
`3xxn`

ANSWER :D
Discussion
9479.

STATEMENT-1 The points A(2, 9, 12), B(1, 8, 8), C(-2, 11, 8) and D(-1, 12, 12) are the vertices ofrhombus. and STATEMENT-2 : AB = BC = CD = DA and AC ne BD then the quadrilateral ABCD is called a rhombus.

Answer»

STATEMENT-1 is TRUE, Statement-2 is true, Statement- is a CORRECT EXPLANATION for Statement -1
Statement-1 is True, Statement-2 is true, Statement- is NOT a correct explanation for Statement -1
Statement-1 is True, Statement-2 is FALSE
Statement-1 is False, Statement-2 is true

Answer :D
Discussion
9480.

If (z - i)/(z +1) is purely imaginary then the locus of z = x +iy is

Answer»

`X^(2) + y^(2) - x + 6Y = 0`
`x^(2) + y^(2) - x - y= 0`
`x^(2) + y^(2) + x - y = 0`
`x^(2) + y^(2) = 1`

ANSWER :C
Discussion
9481.

Write the value of sin^-1 x + cos^-1 x from the following :

Answer»

`1`
`π`
`0`
`π/2`

ANSWER :D
Discussion
9482.

Evalute the following integrals int (2x + 3)/(sqrt(x^(2) + 3x - 4)) dx

Answer»


Answer :`2 SQRT(X^(2) + 3x - 4 ) `+ C
Discussion
9483.

Evaluate the integrals by using substitution int_(-1)^(1)(dx)/(x^(2)+2x+5)

Answer»


ANSWER :`pi/8`
Discussion
9484.

If a circle cuts x ^(2) + y ^(2) =a ^(2) orthogonally and passes through the point ((a ^(2) p)/( p ^(2) + q^(2)), (a ^(2)q )/( p ^(2) + q ^(2))), then it will also pass through

Answer»

`(p,0)`
`(0,Q)`
`(p,q)`
`(AP,aq)`

Answer :C
Discussion
9485.

If the locus of the image of the point (lambda^(2), 2lambda) in the line mirror x-y+1=0 (where lambda is a parameter) is (x-a)^(2)=b(y-c) where a, b , c in I, then the value of ((a+b)/(c+b)) is equal to

Answer»


ANSWER :0.6
Discussion
9486.

If a ne p, b neq, c ne r and |{:(b,b,c),(p+a, q+b, 2c),(a,b,r):}|=0 then (p)/(p-a) + (q)/(q-b) + (r )/(r-c) is equal to

Answer»

0
1
2
3

Answer :C
Discussion
9487.

Find n"if" P (n,4)=12.P(n,2)

Answer»

SOLUTION :`""^nP_4=12xx""^nP_2`
` or,(N!)/((n-4)!)=12xx(n!)/((n-2)!)`
`or, (n-2)! =12(n-4)!`
`or,(n-2)(n-3)(n-4)! =12(n-4)!`
`or,(n-2)(n-3)=12`
`or,n^2-5n-6=60`
`(n-6)(n+1)=0`
`or, n=6-1`
HENCE `n=6` as n is a natural NUMBER.
Discussion
9488.

A=sin78^(@)-sin18^(@)+cos132^(@) B=cos12^(@)+cos84^(@)+cos132^(@)+cos156^(@) and C=(sin 75^(@)+sin 15^(@))/(cos 75^(@)+cos 15^(@)) then arrange in the ascending order

Answer»

C,A,B
B,A,C
A,C,B
A,B,C

Answer :B
Discussion
9489.

If (1+x)^(n) = c_(0) + C_(1)x+C_(2)x^(2)+"….."+X_(n)x^(n), m ge 2 C_(0) - C_(1)+C_(2) - "……"+(-1).^(m-1)C_(m-1) = (-1)^(m-1).^(n-1)C_(m-1).

Answer»

`(-1)^(m-1).^(N-1)C_(m-1)`
`(-1)^(m-1).^(n)C_(m-1)`
`(-1)^(m-1).^(n-1)C_(n-m)`
`(1)^(m-1).^(n)C_(n-m)`

ANSWER :A
Discussion
9490.

int_(0)^(pi//2) (a cos^(2) x+b sin^(2) x) dx

Answer»


ANSWER :`(PI)/(4)( a+b)`
Discussion
9491.

If the lines (x-1)/(1)=(y-4)/(c)=(z+3)/(-3) and (x+1)/(-c)=(y-3)/(2)=(z-1)/(1) are perpendicular then c= …..........

Answer»

`3/5`
`(-3)/(5)`
`-3`
3

Answer :D
Discussion
9492.

A 10 m long horizontal wire extends from North east ro South East. It is falling with a speed of 5.0 ms^(-1), at right angles to the horizontal component of the earth's magnetic field, of 0.3xx10^(-4)Wb//m^(2). The value of the induced emf in wire is :

Answer»

`1.5xx10^(-3)V`
`1.1xx10^(-3)V`
`2.5xx10^(-3)V`
`0.3xx10^(-3)V`

SOLUTION :NA
Discussion
9493.

If a_1 , a_2 and a_3 are three numbers satisfying a_1^2 + a_2^2 +a_3^2 = 1 , then the maximum value of(4a_1- 3a_2)^2 + (5a_2- 4a_3)^2+ (3a_3 - 5a_1)^2 is k, then [ (k)/(14)]is equal to (where [.] denotes the greatest integer function)

Answer»

1
2
3
4

Answer :C
Discussion
9494.

If I_(1)=int_(x)^(1)(1)/(1+t^(2)) dt and I_(2)=int_(1)^(1//x) dt "for" x gt0 then,

Answer»

`I_(1)=I_(2)`
`I_(1)gtI_(2)`
`I_(2)=I_(1)`
none of these

Solution :PUTTING `t=(1)/(u)"in" I_(1)`, we GET
`I_(1)=UNDERSET(1//x)overset(1)int(1)/(1+(1)/(u^(2)))(-(1)/(u^(2)))du=-underset(1//x)overset(1)int(du)/(u^(2)+1)=underset(1)overset(1//x)int du=I_(2)`
Discussion
9495.

Ifcosx +cos^2x=1 , thenthe valueof sin ^4 x + sin ^6xisequalto

Answer»

` -1 + SQRT(5) `
` (-1-sqrt(5))/( 2)`
`(1-sqrt(5))/(2)`
`(-1sqrt(5))/(2)`

ANSWER :D
Discussion
9496.

P is any point inside or on the boundary of Delta ABC having perimeter p and area Delta R is any point in the plane of Delta ABC such that PR le 5. the area of the region in which the point R lies is

Answer»

`25 pi + 5 p + Delta`
`5 pi + 25 P + Delta`
`5 pi + 5 P + Delta`
`5(pi + p) + 25 Delta`

ANSWER :A-q, B-r, C-p, D-p
Discussion
9497.

Solve as directed: 5x + 7 lt 32 in integers, in non-negative integers.

Answer»

Solution :5x + 7 `lt` 32
`rArr 5x+7-7 lt 32-7`
`rArr 5x lt 25`
`rArr (5x)/5 lt (25)/5`
`rArr x lt 5`
If x `in` Z then the solution set isS = {x:x `in` Z and x `lt` 5}
={……. -3,-2,-1,0,1,2,3,4} If x is a NON negative solution then the solution set is
S = { x: x is a non negative INTEGER `lt` 5} = {0,1,2,3,4}
Discussion
9498.

If the equations x^(2)-ax+bc=0 and x^(2)+bx+ca=0 have a common root, then a + b + c =

Answer»

0
1
-1
3abc

Answer :A
Discussion
9499.

If alpha, beta , gamma are the roots of x^(3) + qx + r = 0then the equation whose roots (beta - gamma)^(2), (gamma - alpha)^(2), (alpha - beta)^(2)is

Answer»

`X^(3) + 6qx^(2) + 9q^(2)x + 4q^(2) + 27r^(2) = 0 ` is
`x^(3) + 2qx^(2) + 9q^(2)x + 4q^(2) + 27 = 0 `
`x^(3) + 3qx^(2) + 6q^(2)x + 2Q^(2) + 27 = 0 `
`x^(3) + qx^(2) + 3q^(2)x + 6q^(2) + 27 = 0 `

Answer :1
Discussion
9500.

Let A be a set containing ten elements. Then the number of subsets of A containing at least four elements is

Answer»

845
848
850
854

Answer :B
Discussion