Explore topic-wise InterviewSolutions in .

This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.

10051.

Statement-I: int_(0)^((pi)/(2))sin^(n)xdx=int_(0)^((pi)/(2))cos^(n)xdx,ninN Statement-II: int_(0)^(a)f(x)dx=int_(0)^(a)f(a-x)dx

Answer»


ANSWER :A
Discussion
10052.

Let A and B be two events with P(A^(c)) = 0.3, P(B) = 0.4 "and" P(A cap B^(c))"is equal to"

Answer»

`1/4`
`1/3`
`1/2`
`2/3`

ANSWER :A::D
Discussion
10053.

The range of f(x)=sqrt(|x|-x) is:

Answer»

`(0,OO)`
`[0,oo)`
`(-oo,0)`
`(-oo,0]`

ANSWER :B
Discussion
10054.

You are given the following results on two variables X and Y:barx=36, bary=85, sigma_(x) =11, Var (Y) = 64 and r (X, Y) = 0.66. Find the regression equations and estimate the value of x when y= 75.

Answer»


SOLUTION :N/A
Discussion
10055.

Show that y = sin ( m sin^(-1)x) is a solution of the differential equation(1 - x^(2)) y '' + xy' + m^(2) y = 0

Answer»


Answer :` :. " " y = (m SIN ^(-1)X) ` is a solution of the GIVEN differential equation
Discussion
10056.

If (1+x)^n=c_0+c_1x+c_2x^2+….+c_nx^n, find the value of c_0-c_2+c_4-….

Answer»


ANSWER :`2^(n/2)COS(NPI)/(4)`
Discussion
10057.

If the triangle with vertices at 2hat(i)+hat(j),2hat(j)+hat(k),mhat(k)+hat(i) has centroid hat(i)+hat(j)+hat(k), then m =

Answer»

1
-1
2
3

Answer :C
Discussion
10058.

Two godowns A and B have grain capacity of 100 quintals and 50 qunitals respectively. They supply to 3 ration shops, D,E and F whose requirements are 60,50 and 40 quintals repectively.The cost of transportation per quintal from the godowns to the shops are given in the following table: How should the supplies be transported in order that the transportation cost is minimum? Whatis the minimum cost?

Answer»

Solution :LET the supply of wheat is `x` QUINTAL from A to D and `y` quital from A to E. Then wheat supply will be `(100-x-y)` quintal from A to F. Similarly, `(60-x),(50-y),(x+y-60)` quintals of wheat will be supplied from B to D,E,F respectively.

Now minimum TRANSPORTATION cost
`Z=6x+3y+2.50(100-x-y)+4(60-x)`
`+2(50-y)+3(x+y-60)`
`=2.50x+1.50y+410`
and constraints `xge0, YGE0`
`100-x-yge0impliesx+yle100`
`60-xge0impliesxle60`
`50-yge0impliesyle50`
`x+y-60ge0impliesx+yge60`
First we draw the graph of the lines `x+y=100, x=60,y=50,x+y=60`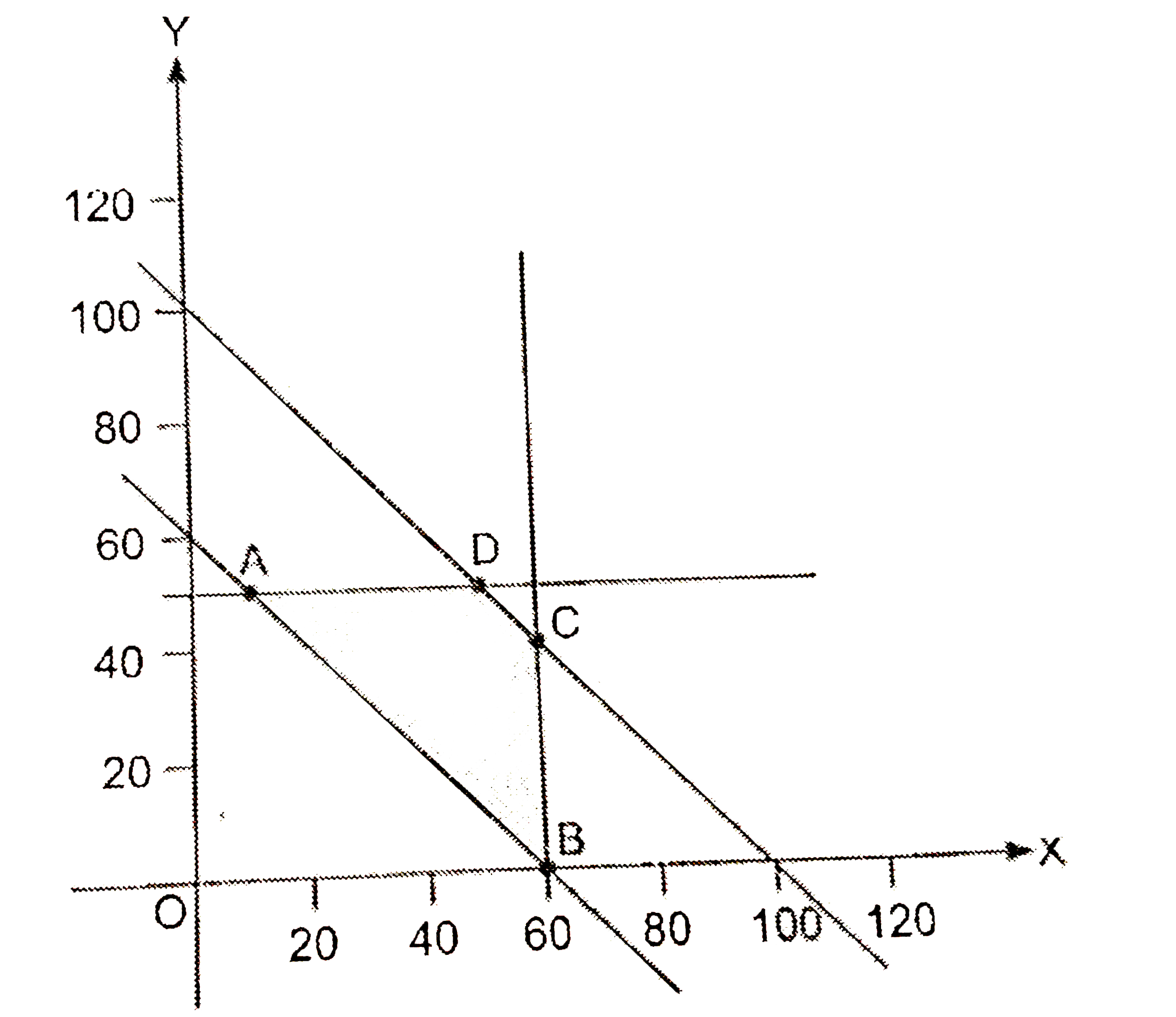

Now, we FIND the feasible region by constraints `x+yle100,xle60,yle50,x+yge60,xge0,yge0` and shade it. Its vertices are `A(10,50),B(60,0),C(60,40),D(50,50)`, at which we find the value of `Z`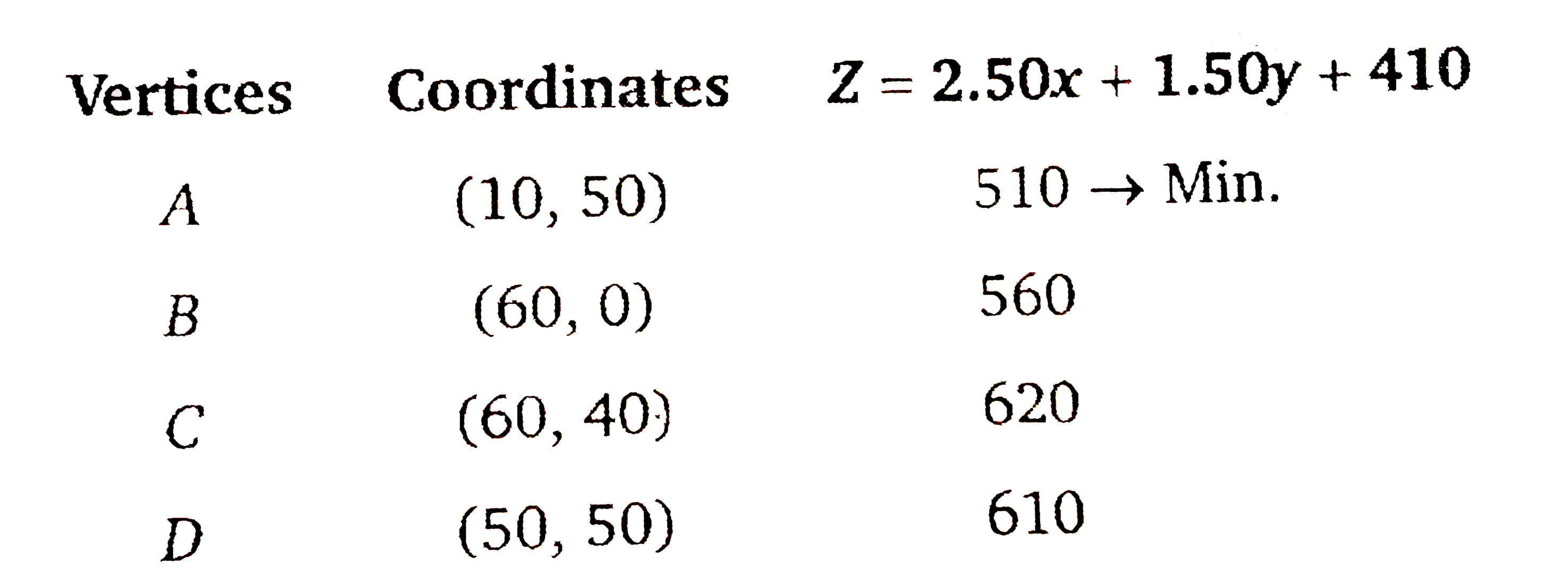

Therefore, minimum transportation cost `Rs. 510`
For this 10,50,40 quintals will supply from A to D E,F respectively and 50,0,0 quintals will supply from B to D,E,F respectively.
Discussion
10059.

One of the most important techniques of counting is the principle of exclusion and inclusion. Let A_(1),A_(2)….A_(m) be m sets and n(A_i) represents the cordinality of the set A, (the number of elements in the set A_i), then according to the principle of exclusion and inclusion.sum_(i=1)^(m)n(A_i)-sum_( i ne j) n (A_i cap A_j)+sum_(i ne j ne k) n(A_(i) cap A_(j) cap A_(k))-.....+(-1)^(n)n(A_(1) cap A_(2) cap ....cap A_(m)). In particular , if A,B,C are three sets, then n ( A cap B cap C ) =n(A)+n(B)+n(C ) -n(A cap B)- n(B cap C)- n(C cap A)+n(A cap B cap C). Principle of exclusion and inclusion must be applied whenever there is a chance of repeated counting of some of the samples. The number of numbers from 1 to 100, which are neither divisible by 3 nor by 5 nor by 7 is .

Answer»

67
55
45
33

Answer :C
Discussion
10060.

One of the most important techniques of counting is the principle of exclusion and inclusion. Let A_(1),A_(2)….A_(m) be m sets and n(A_i) represents the cordinality of the set A, (the number of elements in the set A_i), then according to the principle of exclusion and inclusion.sum_(i=1)^(m)n(A_i)-sum_( i ne j) n (A_i cap A_j)+sum_(i ne j ne k) n(A_(i) cap A_(j) cap A_(k))-.....+(-1)^(n)n(A_(1) cap A_(2) cap ....cap A_(m)). In particular , if A,B,C are three sets, then n ( A cap B cap C ) =n(A)+n(B)+n(C ) -n(A cap B)- n(B cap C)- n(C cap A)+n(A cap B cap C). Principle of exclusion and inclusion must be applied whenever there is a chance of repeated counting of some of the samples. The number of natural numbers less than or equal to 2985984, which are neither perfect squares nor perfect cubes is.

Answer»

2984124
2984244
2959595
none of these

Answer :A
Discussion
10061.

One of the most important techniques of counting is the principle of exclusion and inclusion. Let A_(1),A_(2)….A_(m) be m sets and n(A_i) represents the cordinality of the set A, (the number of elements in the set A_i), then according to the principle of exclusion and inclusion.sum_(i=1)^(m)n(A_i)-sum_( i ne j) n (A_i cap A_j)+sum_(i ne j ne k) n(A_(i) cap A_(j) cap A_(k))-.....+(-1)^(n)n(A_(1) cap A_(2) cap ....cap A_(m)). In particular , if A,B,C are three sets, then n ( A cap B cap C ) =n(A)+n(B)+n(C ) -n(A cap B)- n(B cap C)- n(C cap A)+n(A cap B cap C). Principle of exclusion and inclusion must be applied whenever there is a chance of repeated counting of some of the samples. On a particular day, six persons -pick six-different books, one each, from different counters at a public library. At the closing time , they arbitrarily put their books, to the vacant counters. The probability that exactly two books are at their previous places is .

Answer»

`(1)/(3)`
`(1)/(15)`
`(3)/(4)`
`(3)/(16)`.

Answer :D
Discussion
10062.

Lety^(2) =16x be a given parabola and L be an extremity of its latus rectum in the first quadrant . If a chord is drawn through L with slope -1, then the length of this chord is

Answer»

A) 32
B) `16sqrt2`
C) ` 16sqrt3`
D) ` 32sqrt2`

ANSWER :D
Discussion
10063.

A = {n/n is a digit in the number 33591} and B={n//n in N, n lt 10}, then B-A=

Answer»

{2, 4, 6, 8}
{7, 2, 4, 8, 6}
{1, 3, 5, 7}
{(1, 2), (1, 3), (2, 3)}

Answer :B
Discussion
10064.

Find the equation and length of the common chord of the following circles. x^2 + y^2 - 5x - 6y + 4 = 0, x^2 + y^2 - 2x -2 = 0

Answer»


ANSWER :`x+2y-2=0,2sqrt((14)/5)`
Discussion
10065.

LetS_1 = underset( j=1)overset( 10)sumj (j-1)""^(10)C _(p),S_(2) = underset( j=1)overset( 10 )sum j^(10)andS_(3)= underset(j=1)overset(10)sumj ^(2)""^(10) C_(j) Statement -1S_(3) = 55 xx2 ^(9). Statement -2S_(1)= 90 xx 2^(8) andS_(2)= 10 xx 2 ^(8)

Answer»

STATEMENT -1IS true , statement -2is truestatements-2 isa correctexplanationfor statement -1
Statement -1istrue, statement-2istruestatement-2is nota correctexplanationfor statement -1
Statement -1is truestatement-2is FALSE
Statement -1is false, statement -2istrue

Answer :C
Discussion
10066.

The value of sum_(r=0)^(3) ""^(8)C_(r)(""^(5)C_(r+1)-""^(4)C_(r)) is "_____".

Answer»


SOLUTION :`underset(r=0)overset(3)sum.^(8)(C_(r+1)-.^(4)C_(r))=underset(r=0)overset(3)sum.^(8)C_(r).^(4)C_(r+1)`
`= .^(8)C_(0) XX.^(4)C_(1)+.^(8)C_(1)xx.^(4)C_(2)+.^(8)C_(2)xx.^(4)C_(3)+.^(8)C_(3)xx.^(4)C_(4)`
`=` coefficient of `x^(3)` in `(1+x)^(4)(1+x)^(8)`
`=` coeficient of `x^(3)` in `(1+x)^(12)`
`=.^(12)C_(3) = 220`
Discussion
10067.

Find the solutions set of i) x^(2)+x-12 le 0 ii) x^(2)-2x+1 lt 0 iii) 2-3x-2x^(2) ge 0 over R by both algebric and graphical methods. iv) 15x^(2)+4x-4 le 0

Answer»


Answer :i) `{X in R: -4 le x le 3}` ii) Solution does not exist III) `-2 le x le (1)/(2)` iv) `(-2)/(3) lt x lt (2)/(3)`
Discussion
10068.

Evaluate int_(0)^(pi/2) sin x dx as the limit of a sum.

Answer»


ANSWER :1
Discussion
10069.

Prove that {2,4,6,8,10,…..} set are equivalent.

Answer»

Solution :LET g :A rarr C DEFINED as g(x) =2x -1 CLEARLY F is bijective.
`implies` There is a one-to-one correspondence between A to C
`:.` A and C are equivalent.
Discussion
10070.

If (1+px+x^(2))^(n)=1+a_(1)x+a_(2)x^(2)+…+a_(2n)x^(2n). Which of the following is true for 1 lt r lt 2n

Answer»

`(np+pr)a_(R )=(r+1)a_(r+1)+(r-1)a_(r-1)`
`(np-pr)a_(r )=(r+1)a_(r+1)+(r-1-2n)a_(r-1)`
`(np-pr)a_(r )=(r+1)a_(r+1)+(r-1-n)a_(r-1)`
`(2np+pr)a_(r )=(r+1+n)a_(r+1)+(r+1-n)a_(r-1)`

SOLUTION :`(b)` Differntiating the EXPANSION we have
`n(p+2x)(1+px+x^(2))^(n-1)`
`=a_(1)+2a_(2)x+3a_(3)x^(2)+….+2na_(2n)x^(2n-1)`
Multiplying by `(1+px+x^(2))`
`n(p+2x)(1+a_(1)x+a_(2)x^(2)+….)`
`=(1+px+x^(2))(a_(1)+2a_(2)x+3a_(3)x^(2)+...+2na_(2n)x^(2n-1))`
Comparing coefficient of `x^(r )` both SIDE.
`n[pa_(r )+2a_(r-1)]=(r+1)a_(r+1)+pra_(r )+(r-1)a_(r-1)`
`:.(np-pr)a_(r )=(r+1)a_(r+1)+(r-1-2n)a_(r-1)`
Discussion
10071.

The solution of the differential equation (dy)/(dx) = (xy + y)/(yx + x)is

Answer»

`x+y = LOG ((Cy)/(x))`
`x+y = log(C XY)`
`x-y = log ((CX)/(y))`
`y-x = log ((Cx)/(y))`

Answer :D
Discussion
10072.

If int_(0)^(pi//2) ln (sin x) dx= - pi/2 ln 2 then int_(0)^(pi) ln (1+ cos x) dx=

Answer»

`PI LN 2`
`- pi ln 2`
`pi/2 ln 2`
ln 2

Answer :B
Discussion
10073.

Find the values of a and b that f(x) = {{:(5",","if"x le 2),(ax+b",","If"2 lt x lt 10),(21",",if x ge 10):}is a continuous function

Answer»


ANSWER :`b=1`
Discussion
10074.

Differentiate the following w.r.t.x (cosx)/(logx),xgt0

Answer»

Solution :`d/dx((cosx)/(logx))=(LOG"X"xxsinx-cos"x"xx1/x)/(logx)^2=(-xlogxsinx+cosx)/(XLOGX)^2`
Discussion
10075.

p (2,3,-4) ,vecb =2 hati - hatj + 2 hatk Sum of the length of the intercepts made by the above plane on the coordinate axes is :

Answer»

14
`91//12`
`9//7`
`5//7`

ANSWER :B
Discussion
10076.

Internal bisector of /_A of triangle ABC meets side BC at D.A. line drawn through D perpendicular to AD intersects the side AC at E and the side AB at F. If a, b, c represent the sides of DeltaABC, then :

Answer»

Ae is H.M. Between B and C
`AD=(2bc)/(b+c)cos.(A)/(2)`
`AF=(4bc)/(b+c)sin.(A)/(2)`
the TRIANGLE AEF is isosceles

Answer :A::B::C::D
Discussion
10077.

Evaluate the definite integrals int_(pi/6)^(pi/4)cosecxdx

Answer»


ANSWER :`LOG((sqrt2-1)/(2-sqrt3))`
Discussion
10078.

Find the values of k so that the function f is continuous at the indicated point f(x) = {((k cos x)/(pi-2x)",","if" x ne (pi)/(2)),(3,"if" x= (pi)/(2)):} " at " x= (pi)/(2)

Answer»


ANSWER :k=6
Discussion
10079.

For a positive integer n show that (1+isqrt3)^n+(1-isqrt3)^n=2^(n+1) "cos"(npi)/3

Answer»

Solution :`L.H.S.=(1+isqrt3)^n+(1-isqrt3)^n`
`{2(1/2+isqrt3/2)}^n+{2(1/2-isqrt3/2)}^4`
`=2^n{("COS"pi/3="ISIN"pi/3)^n+("cos"pi/3-"isin"pi/3)}^n`
`=2^n("cos"(npi)/3+"isin"(npi)/3+"cos"(npi)/3-"sin"(npi)/3)`
`=2^n 2"cos"(npi)/3=2^(n+1)"cos"(npi)/3=R.H.S`
Discussion
10080.

Examine the continuity of the function f(x)= {((x^(2))/(2)",","if " 0 le x le 1),(2x^(2)-3x + (3)/(2)",","if " 1 lt x le 2):} at x=1

Answer»


ANSWER :x=1
Discussion
10081.

A : Ifcot A + cot B + cos C = sqrt(3) " then " Delta ABCis an equilateral triangle R: If a^(2) + b^(2) + c^(2) =0 then a=b=c .

Answer»

A is TRUE , R is true and R is correct EXPLANATION of A
A is true , R is TRUEAND R is not correct explanation of A
A is true , R is FALSE
A is false , R is true

Answer :A
Discussion
10082.

The straight line x + 2y = 1 meets the coordinate axes at A and B. A circle is drawn through A,B and the origin. Then, the sum ofperpendicular distances from A and B on the tangent to the circle at the origin is

Answer»

`2sqrt5`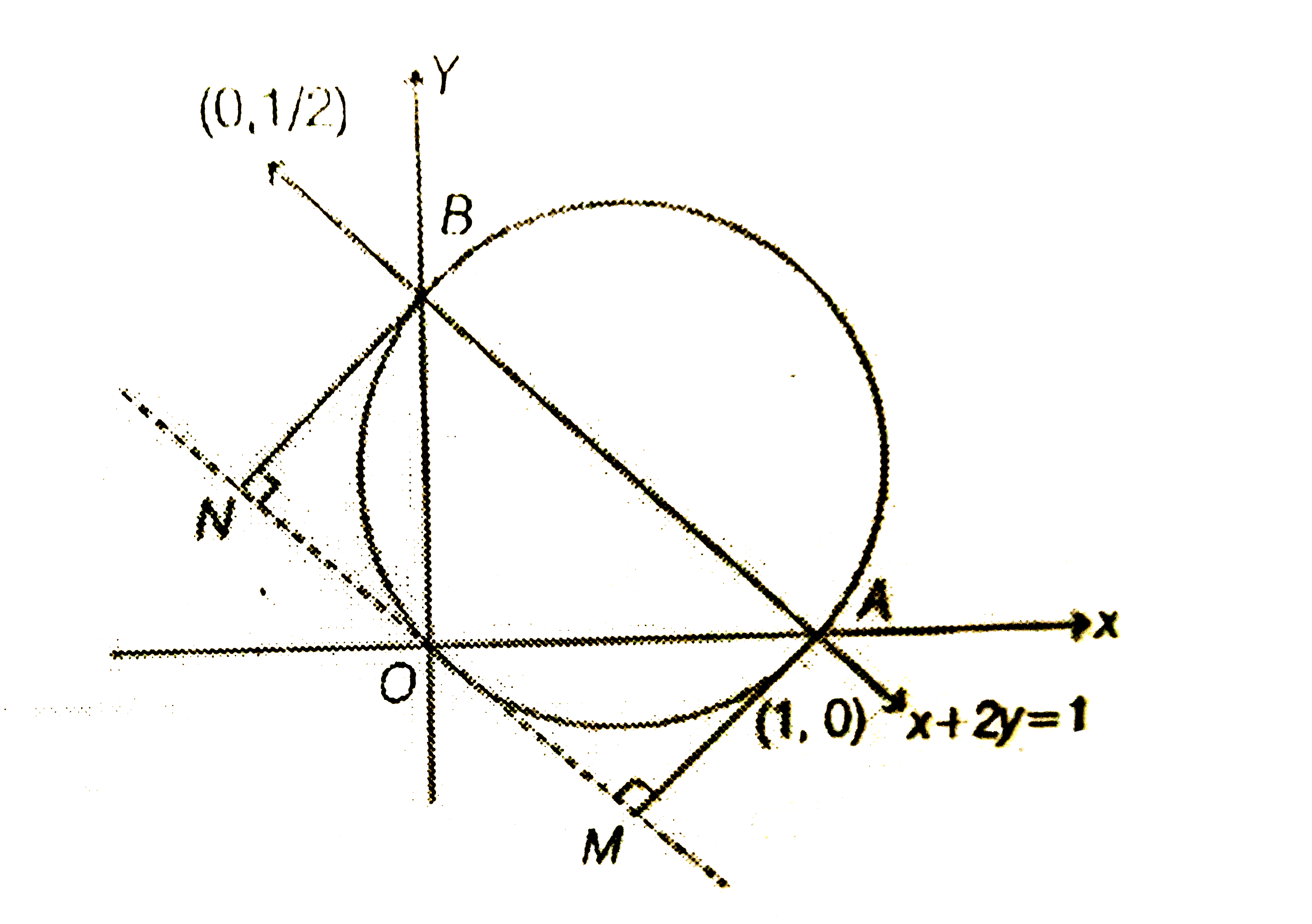
`(sqrt5)/(4)`
`4sqrt5`
`(sqrt5)/(2)`

Solution :According to given information, we have the following figure.

From figure, equation of circle (DIAMETER form) is
`(X-1)(x-0)+(y-0)((y-(1)/(2))=0`
`rArr x^(2) + y^(2) -x -(y)/(2)=0`
Equation of tangent at (0, 0) is `x+(y)+(2) = 0`
`[therefore" equation of tangent at "(x_(1),y_(1)) " is given by " T=0 " Here ", T = 0`
`rArr "xx"_(1)+yy_(1)-(1)/(2)(x+x_(1))-(1)/(4)(y+y_(1))=0]`
`rArr2x + y =0 `
Now, `AM=(|2.1+1.0|)/(sqrt5)=(2)/(sqrt5)`
`[therefore " distance of a point " P(x_(1), y_(1))`from a line
`ax+by + c=0 " is " (|ax_(1)+by_(1)+c|)/(sqrt(a^(2)+b^(2)))]`
and `BN = (|2.0+1((1)/(2))|)/(sqrt5)=(1)/(2sqrt5)`
`therefore AM+BN=(2)/(sqrt5)+(1)/(2sqrt5)=(4+1)/(2sqrt5)=(sqrt5)/(2)`
Discussion
10083.

A gunman has four bullets, he fires till he makes first hit on the target. The probability of a hit for each shot is 0.7, find the probability distribution of the number of bullets used.

Answer»

<P>

ANSWER :`{:(X = x,1,2,3,4),(P(X = x),0.7,0.21,0.063,0.027):}`
Discussion
10084.

If I_(n) = int(logx)^(n) dx then prove that I_(n) = x(logx)^(n) - nI_(n-1) and hence evaluate int(log x)^(4) dx

Answer»


ANSWER :`x[LOGX)^(4)-4(logx)^(3)+12(logx)^(2)-24logx+24]+c`
Discussion
10085.

In 2007, how many industry groups consisted of more than 1 million employees?

Answer»

`0`
`1`
`2`
`3`

ANSWER :C
Discussion
10086.

A bag X contains 2 white and 3 red balls and bag Y contains 4 white and 5 red balls. One ball is drawn at random from one bag and it is found to be red. Find the probability that it was drawn from bag Y.

Answer»


ANSWER :`(25)/(52)`
Discussion
10087.

If y=tan^(-1)((sin x + cos x)/(cos x - sin x)), then (dy)/(dx) is equal to

Answer»

`1//2`
`pi//4`
0
1

Answer :D
Discussion
10088.

Vectors a and b are inclined at an angle theta=120^(@). If |a|=1, |b|=2, then [(a+3b)xx(3a+b)]^(2) is equal to

Answer»

190
275
300
192

Solution :Given ,`|a|=1,|b|=2`
`THEREFORE [(a+3b)xx(3a+b)]^2=[0+axxb+9bxxa+0]^2`
`=[-8axxb]^2=64[|a|^2|b|^2sin^2theta]`
`=64[1xx4xxsin^2 120^@]`
`=64xx4xx(3)/(4)=192`
Discussion
10089.

Find the equation of pair of tangents from (i) (0,0) to the circle x^(2)+y^(2)+10x+10y+40=0 (ii) (4,10) to the circle x^(2)+y^(2)=25 (iii) (3,2) to the circle x^(2)+y^(2)-6x+4y-2=0 (iv) (10,4) to the circle x^(2)+y^(2)=25 (v) (1,3) to the circle x^(2)+y^(2)-2x+4y-11=0

Answer»


ANSWER :(i) 0 (ii) 0 (iii) 0 (iv) 0 (iv) `0, cos^(-1)(7/25)`
Discussion
10090.

Ifintphi(x)dx=Psi(x)," then "int(phi_(@)h)(x)h(x)h'(x)dx=

Answer»

`(phi_(@)h)(x)PHI'(x)-int(phi_(@)h)(x)h'(x)DX+C`
`(Psi_(@)h)(x)h(x)-int(Psi_@h)(x)h'(x)dx+c`
`(Psi_@h)(x)phi(x)-int(Psi_@h)(x)phi'(x)dx+c`
`(Psi_@Phi)(x)h(x)-int(Psi_@phi)(x)h'(x) dx +c`

ANSWER :B
Discussion
10091.

Let f(x)={(|x-1|+|x-2|, ,, 2ge1),(x, ,, xlt1):} and g(x)={("max"{f(t):x-1letlex}, :, 0lt xlt 2),(-x+3, :, 2ltxle3):} then number of points in[0,3] where g(x) is not differentiable is/are____

Answer»


SOLUTION :`G(x)= {(x, :, 0LEXLE1),(1, :, 1lexle2),(-x+3, :, xgt2):}`
Discussion
10092.

Let P and Q be two sets of real numbers defined as follows: P={theta in R : sin theta - sqrt(3) cos theta = 2 cos theta} Q = {theta in R, cos theta + sqrt(3) sin theta = 2 sin theta}, thnen

Answer»

<P>P = Q
`P cap Q = phi`
`P SUBE Q, P NE Q`
`Q sube P, Q ne P`

ANSWER :A
Discussion
10093.

Find the value of 'alpha' so that range of the function y=(x+1)/(x^(2)+x+alpha), for x in R always contains the set of values [-(1)/(3), 1]

Answer»


ANSWER :`ALPHA LE 1` is the VALUE of `'alpha'`.
Discussion
10094.

Write Minors and Cofactors of the elments of following determinants : |{:(2,-4),(0,3):}|

Answer»


ANSWER :`M_(11)=3,M_(12)=0,M_(21)=-4,A_(22)=2`
`A_(11)=3,A_(12)=0,A_(21)=4,A_(22)=2`
Discussion
10095.

Statement-1: tan{cos^(-1)(1)/sqrt(82)-sin^(-1)(5)/sqrt(26)}=29/3 Statement-2: [x cos(cot^(-1))^(2)=51/50rarr x -(1)/5sqrt(2)

Answer»

Statement-1 is is True, Statement-2 is true, Statement-2 is a CORRECT explanation for Statement-1.
Statement-1 is True, Statement-2 is True, Statement-2 is not a correct explanation for Statement-1.
Statement-1 is True, Statement-2 is False.
Statement-1 is False, Statement-2 is True.

Solution :we have tan `{cos^(-1)(1)SQRT(82)-sin^(-1)(5)/sqrt(26)}`
`=tan (tan^(-1)9-tan^(-1)5)=tan{tan^(-1)(9-5)/(1+9xx5)}`
`=tan(tan^(-1)2/23)=2/23`
so statement 1 is not true
`RARR (x^(2))/sqrt(x^(2)+1)+(1)sqrt(x^(2)+1)^(2)=51/50 rarr x^(2)+1=51/50 rarr x=(1)/(5sqrt(2))`
so statement 2 is true
Discussion
10096.

Find the area in Sq. units bounded by the x-axis , part of the curve y=1+(8)/(x^(2)) and the ordinates x=2 and x=4

Answer»


ANSWER :4
Discussion
10097.

If sets A and B are defined as A={(x,y)//y=e^(x),x in R}, B={(x,y)//y=x,x in R}, then

Answer»

`B sub A`
`A sub B`
`A nn B-phi`
`A uu B=A`

ANSWER :C
Discussion
10098.

When (sin9 theta)/(cos27 theta)+(sin3 theta)/(cos9theta)+(sin theta)/(cos 3 theta)=k (tan 27 theta-tan theta) is defined, then k =

Answer»

`(pi)/(2)`
`-(1)/(2)`
`(1)/(2)`
`(pi)/(4)`

ANSWER :C
Discussion
10099.

Find lambda if the vectors overset(to)(a) = hat(i) +3 hat(j) + hat(k) , overset(to)(b) = 2hat(i) - hat(j) - hat(k) and overset(to) (c ) = lambda hat(i) + 7 hat(j) + 3 hat(k) are coplanar

Answer»


ANSWER :`lambda=0`
Discussion
10100.

Assuming that each child is as likely to be a boy as it is to be a girl, what is the conditional probability that in a family of two children both are boys, given that the older child is a boy.

Answer»


ANSWER :`1//2`
Discussion