InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 12201. |
Consider the equaitonof line abarz + abarz+ abarz + b=0, whereb is arealparameterand a isfixed non-zero complex number. Theinterceptof lineon real axis is given by |
|
Answer» `(-2b)/(a+bara)` Let thePQbe thesegement intercept between AXES. Forintercept on real axis `Z_(R)`. `z =BARZ` `rArr Z_(R)(a+ bara) + b =0` ` rArr Z_(R) = (-b)/(a + bara)` For interceptonimaginary `Z_(1)` `z +barz = 0` `rArr Z_(1)(bara - a) + b=0` `rArr Z_(1)= (b)/(a+bara)` For mid-point, `z= (Z_(R) + Z_(I))/(2)` `rArr z =(-b)/(2)[(1)/(bara+a)+(1)/(bara +a)]` `z= (BARAB)/((a + bara)(a-bara))` `rArr z = (barab)/(a^(2) -(a)^(2))` `(z[a^(2)-(a)^(2)])/(bara) = barz((bara)^(2) - (a)^(2))/(a)` `rArr az + BAR(az) =0` |
|
| 12202. |
Consider the equationof line abarz + baraz + b=0, whereb is arealparameterand a isfixed non-zero complex number. The locus of mid-point of thelineintercepted between real and imaginary axis is givenby |
|
Answer» `az- BAR(az) =0` Let thePQbe thesegement intercept between axes. Forintercept on real axis `Z_(R)`. `Z =barz` `rArr Z_(R)(a+ bara) + b =0` ` rArr Z_(R) = (-b)/(a + bara)` For interceptonimaginary `Z_(1)` `z +barz = 0` `rArr Z_(1)(bara - a) + b=0` `rArr Z_(1)= (b)/(a+bara)` For mid-point, `z= (Z_(R) + Z_(I))/(2)` `rArr z =(-b)/(2)[(1)/(bara+a)+(1)/(bara +a)]` `z= (barab)/((a + bara)(a-bara))` `rArr z = (barab)/(a^(2) -(a)^(2))` `(z[a^(2)-(a)^(2)])/(bara) = barz((bara)^(2) - (a)^(2))/(a)` `rArr az + bar(az) =0` |
|
| 12203. |
Consider the following statements: S_(1): The antiderivative of every function is an odd function. S_(2): Primitive of (3x^(4)-1)/(x^(4)-x+1)^(2) w.r.t is x/(x^(4)+x+1) +C S_(3): int1/(sqrt(sinxcosx))dx = -2/sqrt(tanx)+C S_(4): The value of int(sqrt(a+x)/(a-x)-sqrt(a-x)/(a+x)) dx is equal to -2sqrt(a^(2)-x^(2))+C State, in order whether S_(1),S_(2),S_(3),S_(4) are true or false |
|
Answer» FFTT |
|
| 12204. |
If a matrix has 18 elements, what are the possible orders it can have? What, if it has 5 elements? |
|
Answer» |
|
| 12205. |
If a=hat(i)+hat(j)+hat(k), b=hat(i)+3hat(j)+5hat(k) and c=7hat(i)+9hat(j)+11 hat(k), then the area of the parallelogram having diagonals a+b and b+c is |
|
Answer» `4sqrt(6)` `a = hati +HATJ +hatk, b =hati +3hatj +5 hatj ` and`c=7 hati +9 hatj +1 hatk` Let `A =1 +b=(hati + hatj +hatk) +(hati+3hatj +5 hatk)=2 hati +4 hatj+6hatk` and `=+=(hat+hat3+ha5)+(hat7+hat9+hat11)` `=hat8+hat12+hat16` If A and B are adagonals, then area of parallelogram `1/2|AxxB|=1/2||{:(hati, hatj,hatk),(2,4,6),(8,12,16):}||` `=1/2|hati(64-72)-hatj(32-48)+hatk(24-32)|` `1/2|-8hati+16hatj-8hatk|` `=|-4hati+8hatj+4hatk|` `=sqrt((-4)^(2)+(8)^(2)+(-4)^(2))` `=sqrt(16+64+16)` `=sqrt96=4sqrt6` |
|
| 12206. |
If the function f(x) = {(x, if 0 le x le 2),(2, if x ge 2):} derivable at 2? Justify. |
|
Answer» |
|
| 12207. |
I : The equation of the perpendicular bisecting plane of the line segment joining (-3,3, 2), (9, 5, 4) is x – 7y + 2z - 1 = 0 II : The equation of the plane passing through the points (1, 2, 1), (1, 1, 0), (- 2,2, - 1) is 2x – 3y + 2z – 11 = 0 |
|
Answer» only I is TRUE |
|
| 12209. |
Integration by partial fraction : int(x^(2)-1)/(x^(4)+x^(2)+1)dx=... |
|
Answer» `(1)/(2)LOG((x^(2)+x+1)/(x^(2)-x+1))+C` |
|
| 12210. |
If [sinx]+[sqrt(2)cosx]=-3,x in[0,2pi]([.]-GIF), "then" x in |
|
Answer» `((5PI)/(4),2pi)` `A^(n)-B^(n)=(A+B)(A^(n)-B^(n))-AB(A^(n)-B^(n))` `impliesI=A+B-AB""[becauseA^(n)-B^(n)"is INVERTIBLE"]` `IMPLIES (I-A)(I-B)=0` As A, `B ne l`, we get I-A and I-B are singluar MATRICES. |
|
| 12212. |
Thereare n pointsin a planeno threeofwhichare in thesamelineexceptingp pointswhich arecollinear. Thenumberof triangle fomedby joiningthem is |
|
Answer» `""^(N)C_(2)` |
|
| 12213. |
The volume of a parallelopiped whose coterminous edges are 2a, 2b, 2c, is |
|
Answer» `2 [(a,b,C)]` |
|
| 12214. |
The vector equation of the linepassing through the point i+j-k and parallel to the vector 2i+3j-k is |
|
Answer» R=(i+j-k)+t(2i+3j-k) |
|
| 12215. |
Draw the graph of y = x sin x. |
|
Answer» Solution :We have y = f(x) = x sin x. First draw the graph of `y = +-x`. Now CONSIDER the values of f(x) for quadrant angles. f(0) = 0 `f(pi//2) = pi//2` `f(pi) = 0` `f(3pi//2) = -3pi//2` `f(2pi) = 0` `f(5pi//2) = 5pi//2` ETC. POINTS `(pi//2, pi//2), (5pi//2, 5pi//2), ...` lie on the graph of y = x. Points `(3pi//2, 3pi//2), (7pi//2, 7pi//2),...` lie on the graph of y = -x. Further f(x) = f(-x), hence the function is EVEN and the graph is symmetrical about the y-axis. From the above discussion, the graph of the function is as shown in the following figure. 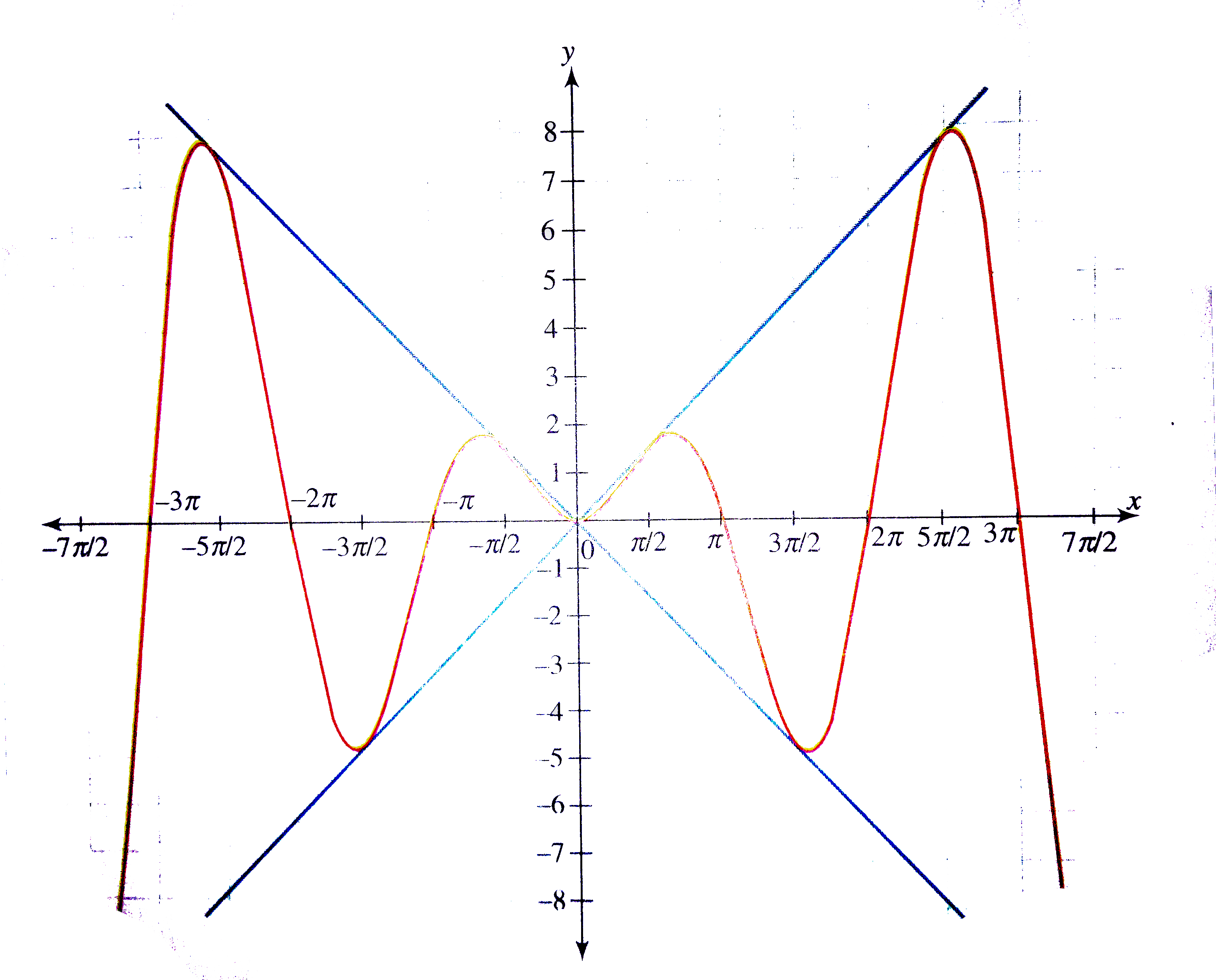
|
|
| 12216. |
If the co-ordinates of the points A, B, C, D be (1,2,3),(4,5,7) (-4,3,-6) and (2,9,2) respectively, then find the angle between the lines AB and CD |
|
Answer» Since 3/6 = 3/6 = 4/8, AB and CD are parallel `rArr` ANGLE between AB and CD = `0^@` |
|
| 12217. |
If P and Q are the Points of intersection of the circles x^2 + y^2 + 3x + 7y -2p - 5 = 0 andx^2 +y^2 +2x +2y- p^2 =0 then there is a circle passing through P, Q and (1, 1) for |
|
Answer» all EXCEPT ONE value of p |
|
| 12218. |
On a multiple choice examination with three possible answers (out of which only one is correct) for each of the five questions, what is the probability that a candidate would get four or more correct answers just by guessing. |
|
Answer» |
|
| 12219. |
The point of extremum of f(x)=int_(0)^(x)(t-2)^(2)(t-1)dt is a |
|
Answer» max at X = 1 |
|
| 12220. |
A tower leans towards west making an angle alpha with the vertical. The angular elevation of B, the top most point of the tower, is 75^(@) as observed from a point C due east of A at a distance of 20 units. If the angular elevation of B from a point due east of C at a distance of 20 units from C is 45^(@), then tan alpha is equal to |
|
Answer» `(sqrt3+1)/(2)` |
|
| 12221. |
The volume of the parallelepiped with edges -12hati+alpha hatk,3hatj-hatk and 2hati+hatj-15hatk is 546 then alpha = …………… |
| Answer» ANSWER :C | |
| 12222. |
If x is a real number then maximum value of (3x^(2)+9x+17)/(3x^(2)+9x+7) is ………… |
| Answer» Answer :B | |
| 12223. |
An experiment succeeds twice as often as it fails. Find the probability that in the next six trials, there will be atleast 4 successes. |
|
Answer» |
|
| 12224. |
Bag I contains 3 red and 4 black balls while another Bag II contains 5 red and 6 black balls. One ball is drawn at random from one of the bags and it is found to be red. Find the probability that it was drawn from Bag II. |
|
Answer» |
|
| 12226. |
Findproducts : [[0,1],[1,0]][[a,b],[c,d]] |
|
Answer» SOLUTION :`[[0,1],[1,0]][[a,B],[C,d]]` `=[[0.a+1.c""0.b+1.d],[1.a+0.c" "1.b+0.d]]=[[c,d],[a,b]]` |
|
| 12227. |
If theta=pi/6, then the 10th term of the series 1+(costheta+isintheta)+(cos theta+i sin theta)^2+…. Is |
|
Answer» i |
|
| 12228. |
Let alpha !=1 be a real root of the equationx^(3)-ax^(2)+ax-1=0, where a != -1 is a real number. Then, a root of this equation, among the following, is |
|
Answer» `ALPHA^(2)` |
|
| 12229. |
1.C_0 + 3.C_1+ 3^2.C_2+….+3^n.C_n = |
|
Answer» `4^n` |
|
| 12230. |
A relation R on a finite set having n elements is reflexive. If R has m pairs then ............ |
| Answer» Solution :N/A | |
| 12231. |
The vector (bar(a)+bar(b)) bisects the angle between the non-collinear vectors bar(a) and bar(b), if …………… |
|
Answer» |
|
| 12232. |
Integrate the functions (x^(3)-1)^(1/3)x^(5) |
|
Answer» |
|
| 12233. |
If A and B are square matrices of order 3 x 3 such that |A|=2,|B|=3, then |2AB| = |
|
Answer» 48 |
|
| 12234. |
Find the number of positive integral solutions of x_(1)x_(2)x_(3)x_(4)=1050. |
|
Answer» |
|
| 12235. |
If A and B are two square matrices of order n , and A and B commute, then for any real number k |
|
Answer» `A-kI,B-kI` COMMUTE |
|
| 12236. |
The equation of the line passing through the point P(1, 2) such that P bisects the part intercepted between the axes is |
|
Answer» a, B, C |
|
| 12237. |
State which of the foolowing statement is true? |
|
Answer» The distance between the line `vecr=(2 HATI-2 hatj+3 HATK)+( hati- hatj+ 4hatk)` and the plane `vecr.( hati+5 hatj+ hatk) =5 is (10)/(3 sqrt3)` units . |
|
| 12238. |
Consider the following sequence :a _(1) = a _(2) =1, a _(1) = 1 + minimum( a _(i-1) , a _(i-2)) for I gt 2. Then a _( 2006)= |
|
Answer» |
|
| 12239. |
If the locus of the mid points of the chords of the ellipse (x^(2))/(a^(2)) +(y^(2))/( b^(2)) =1, drawn parallel to y=m_1x is y=m_2xthen m_1m_2= |
|
Answer» ` ( B^(2))/( a^(2))` |
|
| 12240. |
If sin (sin^(-1)""(1)/5 + cos^(-1)x) = 1, then find the value of x.a) 0 b) 1/5 c) 2/5 d) 3/5 |
| Answer» ANSWER :`X =(1)/5` | |
| 12241. |
If ""^(18)C_(15)+2(""^(18)C_(16))+""^(17)C_(16)+1=""^(n)C_(3), then n = |
|
Answer» 19 |
|
| 12242. |
Evalute the following integrals int ((1 + log x)^(2))/(x )dx |
|
Answer» |
|
| 12243. |
Let A={a,b,c} and Let R={(a,a),(a,b)}. then ,R is |
|
Answer» REFLEXIVE and SYMMETRIC but TRANSITIVE |
|
| 12244. |
Three friends Ram , Shyam and Rahul went to a shop .Ram purchased 12 dozen notebooks ,6 dozen pen and 10 dozen pencil .Shyam purchased 20 dozen notebooks , 10 dozen pen and 15 dozen pencils . If the price of 1 dozen notebooks , pen and pencil is respectively Rs 72, Rs. 48 and Rs. 18 . Using matrix equation find the amount paid by each person to shopkeepar . |
|
Answer» |
|
| 12245. |
Find the number of (i) 6 |
|
Answer» |
|
| 12246. |
Integrate the functions xsinx |
|
Answer» |
|
| 12247. |
Evaluate : (i) int_(0)^(2pi) {sin(sinx)+sin(cosx)}dx, (ii) int_(0)^(pi) (dx)/(5+4cos2x) (iii) int_(0)^(pi//2) (2lnsinx-ln sin2x)dx , (iv) int_(0)^(oo) ln(x+(1)/(x)).(dx)/(1+x^(2)) |
|
Answer» |
|
| 12248. |
If S_(0),S_(1),S_(2),… are areas bounded by the x-axis and half-wave of the curve y=sin pi sqrt(x)," then prove that "S_(0),S_(1),S_(2),… are in A.P… |
|
Answer» SOLUTION :`y= sin pi sqrt(x)` meets x-axis when `pisqrt(x)=npi or x=n^(2), n in N.` Therefore, area of half-wave between `x=n^(2) and x=(n+1)^(2)` is `S_(n)=|overset((n+1)^(2))underset(n^(2))int sin pi sqrt(x)dx |` `"Putting "pisqrt(x)=y and pi^(2) dx =2Y dy,`we get `therefore""S_(n)=|(2)/(pi^(2))overset((n+1)pi)underset(npi)inty sin y dy |` `=|(2)/(pi^(2))[-y cos y + sin y ]_(npi)^((n+1)pi)|` `=|(2)/(pi^(2))[-(n+1)pi cos (n+1) pi +npi cos n pi ]|` `=(2(2n+1))/(pi), n in N` `"Hence, "S_(0),S_(1),S_(2),...` are in A.P.. |
|
| 12249. |
int (tan x+tan^3 x)/(1+tan^3x) dx. |
|
Answer» |
|
| 12250. |
Marks scored by 100 students in a 25 marks unit test ofMathematics is given below. Their median is {:("Marks " ,0-5,5-10,10-15,15-20,20-25),("Students "," "10," "18," "42," "23," "7):} |
|
Answer» 12 |
|