InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 1301. |
Find all common tangents of the pairs of circles x^(2) +y^(2) +4x + 2y -4 =0 and x^(2)+y^(2) -4x -2y +4=0 |
|
Answer» |
|
| 1302. |
Inverse of the matrix [[cos 2 theta,-sin 2 theta],[sin 2 theta , cos 2 theta]] is |
|
Answer» `[[COS2THETA,-SIN2THETA],[sin2theta,cos2theta]]` is |
|
| 1303. |
Let X_(1),X_(2),…….X_(n) be n observations,and let bar(x) be theirarithmeticmeanand sigma^(2) be theirvariance . Statement 1 : Arithmeticmeanof x_(1)+ 2,x_(2) + 2,x_(3) + 2,…..,x_(n) + 2 is bar(x) + 2 Statement2 : Varianceof x_(1) |
|
Answer» Statemnet 1is TURE , STATEMENT 2 is ture, Statement 2 is a correct EXPLANATION for Statement 1 |
|
| 1304. |
Letx_(1),x_(2),………,x_(n)be n observation , and letbar(x)be thrirarithmeticmeanand sigma^(2)be theirvariance. Statement1 : Variance of 2x_(1),2x_(2),…..,2x_(n) is 4sigma^(2). Statement 2 : Arithmetic meanof 2x_(1),2x_(2),......,2x_(n) is 4 bar(x). |
|
Answer» Statemnet 1is ture , Statement 2 is ture, Statement 2 is a correct EXPLANATION for Statement 1 |
|
| 1305. |
The plane (x)/(a)+(y)/(b)+(z)/(c )=3 meets the co-ordinate axes in A,B,C. The centroid of the triangle ABC is |
|
Answer» `((a)/(3),(B)/(3),(C )/(3))` |
|
| 1306. |
Determine the order and degree of the differential equation y' + y = e^(x) |
|
Answer» |
|
| 1307. |
Find the numerically greatest terms in the expansion of(3 + (2x)/(5))^12 whenx = 3/4 |
|
Answer» |
|
| 1308. |
Write minors and cofactors of the elements of following determinant |{:(1,-2),(4,3):}| |
|
Answer» `A_(11)=3,A_(12)-4,A_(21)=2,A_(22)=1` |
|
| 1309. |
Let alpha be a complex p^(th) root of unity with alpha ne 1 . Let p numbers r_(1) , r_(2)…..r_(p) are selected one by one with replacement from a set S where S { 1 , 2 , 3 ..np} , p in N andn in N . Then probability that alpha_(bar r_(1)) , alpha_(barr _(2)) + ... + alpha_(bar r_(p)) = 0 is |
|
Answer» INDEPENDENT of only |
|
| 1310. |
An ellipse E,(x^(2))/(a^(2))+(y^(2))/(b^(2))=1, centred at point O has AB and CD as its major and minor axes, respectively. Let S_(1) be one of thefoci of the ellipse, the radius of the incircle of traingle OCS_(1) be 1 unit, adn OS_(1)=6 units The equation ofthe director circle of E is |
|
Answer» `x^(2)+y^(2)=48.5` 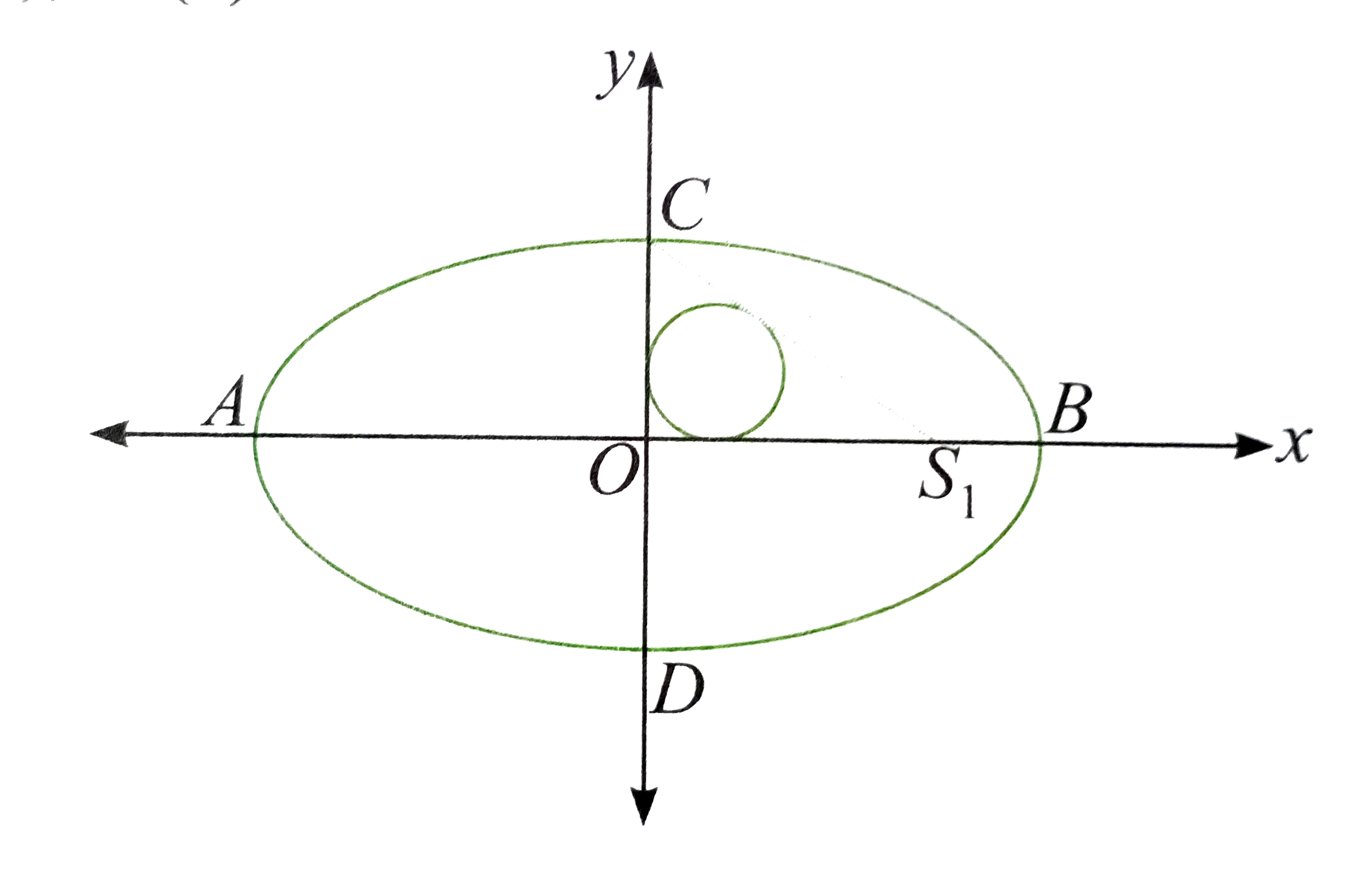 `:.OS_(1)=ae=6,OC=b` Also,` CS_(1)=a` `:. "Area of " DeltaOCS_(1)=(1)/(2)=(OS_(1))xx(OC)=3b` `:.`Semi-perimeter of `DeltaOCS_(1)=(1)/(2)=(OS_(1)+OC+CS_(1))` `=(1)/(2)(6+a+b) ""(1)` `:.` In radius of `DeltaOCS_(1) ","( "Using" r=(Delta)/(S))` =` (3b)/((1)/(2)(6+a+b))=1""("Using"r=(Delta)/(S))` `or 5b=6+a""(2)` Also, `b^(2)=a^(2)-a^(2)e^(2)=a^(2)-36""(3)` From (2), we get `25(a^(2)-36)=36+a^(2)+12a` `or 2a^(2)-a-78=0` `a=(13)/(2),-6` `:. a=(13)/(2) and b=(5)/(2)` Area or ellipse `=piab=(65pi)/(4)` sq. UNIT Perimeter of `DeltaOCS_(1)=6+a+b=6+(13)/(2)+(5)/(2)=15` UNITS The equation of DIRECTOR circle is `x^(2)+y^(2)=a^(2)+b^(2)` or `x^(2)+y^(2)=(97)/(2)` |
|
| 1311. |
An ellipse E,(x^(2))/(a^(2))+(y^(2))/(b^(2))=1, centred at point O has AB and CD as its major and minor axes, respectively. Let S_(1) be one of thefoci of the ellipse, the radius of the incircle of traingle OCS_(1) be 1 unit, adn OS_(1)=6 units The area of ellipe (E) is |
|
Answer» `65pi//4`  `:.OS_(1)=ae=6,OC=b` Also,` CS_(1)=a` `:. "AREA of " DeltaOCS_(1)=(1)/(2)=(OS_(1))xx(OC)=3b` `:.`Semi-perimeter of `DeltaOCS_(1)=(1)/(2)=(OS_(1)+OC+CS_(1))` `=(1)/(2)(6+a+b) ""(1)` `:.` In radius of `DeltaOCS_(1) ","( "Using" r=(Delta)/(S))` =` (3b)/((1)/(2)(6+a+b))=1""("Using"r=(Delta)/(S))` `or 5b=6+a""(2)` Also, `b^(2)=a^(2)-a^(2)e^(2)=a^(2)-36""(3)` From (2), we GET `25(a^(2)-36)=36+a^(2)+12a` `or 2a^(2)-a-78=0` `a=(13)/(2),-6` `:. a=(13)/(2) and b=(5)/(2)` Area or ellipse `=piab=(65pi)/(4)` sq. unit Perimeter of `DeltaOCS_(1)=6+a+b=6+(13)/(2)+(5)/(2)=15` UNITS The equation of director circle is `x^(2)+y^(2)=a^(2)+b^(2)` or `x^(2)+y^(2)=(97)/(2)` |
|
| 1312. |
f(x)= {((1)/(e^(4x) + 1)",",x ne 0),(0",",x = 0):} Examine the continuity of f(x) at x= 0 |
|
Answer» |
|
| 1313. |
Let S be a non-empty subset of R. consider the following statement : P: There is a rational number xinS such that xgt0. which of the following statements is the negation of the statement P? |
|
Answer» `x in S` and `x LE 0 RARR x` is not rational `~p `: Every rational number `x in S` satisfies `xle0` |
|
| 1314. |
If 1/2lt|x|lt1 then which of the following are real ? |
|
Answer» `SQRT(3)`when `x GT1` |
|
| 1315. |
Find the number of 5 letter words that can be formed using the letters of the word “NATURE' that begin and end with vowel when repetitions are allowed. |
|
Answer» |
|
| 1317. |
The perimeter of rectangle ABCD is 96 cm. The ratio of the side lengths AB : BC is 3:5. What is the length, in centimeters of bar(AB)? |
|
Answer» 6 |
|
| 1319. |
Obtain the parametric equation of each of the following circles. 4(x^(2)+y^(2))=9 |
|
Answer» |
|
| 1320. |
A die is rolled twice. Getting a number greater than 4 is called a 'Success'. Let the random variable X is equal to the number of successes then mean of X is |
|
Answer» `(1)/(3)` |
|
| 1321. |
The value of int_(1)^(a)[x] f' (x) dx, a gt 1, where [x] denotes the greatest integer not exceeding x is |
|
Answer» `AF(a)-{F(1)+f(2)+....+ f([a])}` |
|
| 1322. |
Solve as directed : Convert to linear inequality and solve for natural numbers: (x-2) (x-3) lt (x +3) (x-1) |
|
Answer» SOLUTION : (x-2) (x-3) `lt` (x +3) (x-1) `RARR x^2 - 5X + 6 lt x^2 + 2X-3` `rArr -5x + 6 lt 2x - 3` `rArr -5x - 2x lt -3 -6 `rArr -7X lt -9 `rArr x gt 9/7` If x `in` N the solution set is S = { 2,3,4…….} |
|
| 1324. |
Show that the focal chord of the parabola y^(2)=4ax, which makes an angle alpha with the x-axis, is of length 4a cosec^(2) alpha. |
|
Answer» |
|
| 1325. |
Let f:R rarr R be a continuous function such that f(x)-2f(x/2)+f(x/4)=x^(2). f(3) is equal to |
| Answer» ANSWER :d | |
| 1326. |
A random variable X takes four values with probabilities (1+3x)/(4), (1-x), (1+2x)/(4) and (1-4x)/(4). Find the set of values of x for the variable X to have probability distribution. |
|
Answer» |
|
| 1327. |
Two poles standing on a horizontal ground are of heights 5 m and 10 m respectively. The line joining their tops makes an angle of 15^(@) with the ground. Let d be the distance (in m) between their poles, then (2 - sqrt(3))d = ______________ |
|
Answer» |
|
| 1328. |
A questionpapercontains6questioneachhavinganalternative. Thenumberofwaysthatanexaminecananswer oneor morequestion is |
|
Answer» 243 |
|
| 1329. |
A=[aij]_(mxxn) is a square matrix, ifa) m=nb) m>nc) m< n d) none of these |
|
Answer» mltn |
|
| 1330. |
Find the transpose of each of each of the following matrics: [[5],[1/2],[-1]] |
| Answer» SOLUTION :`[[5,1/2,-1]]` | |
| 1331. |
A number x is chosen at random from the set {1,2,3,4,. . . . ,100} . Define the events A =the chosen number x satisfies((x - 10) (x - 50))/((x - 30)) ge 0 . Then P(A) is |
|
Answer» `0 . 71` |
|
| 1332. |
The roots of (z-1)^n=i(z+1)^n are plotted on the argand plane they are |
| Answer» Answer :A | |
| 1333. |
Dot product of a vector vec(a) with hati+hatj-3hatk,hati+3hatj-2hatk and 2hati+hatj+4hatk are 0, 5 and 8 respectively. Find the vector. |
|
Answer» |
|
| 1334. |
The sum to infinite terms of the series (3)/(10)+(3.7)/(10.15)+(3.7.9)/(10.15.20)+..." to " oo is |
|
Answer» `root4(125)-1` |
|
| 1335. |
If [x] represents greatest integer le x then int_(0)^(sqrt(2))[x^(2)]dx= |
|
Answer» `2-SQRT(2)` |
|
| 1336. |
Following is the graph of y = f'(x) and f(0) = 0 . (a) What type of function y = f'(x) is ? Odd or even? (b) What type of function y = f(x) is ? Odd or even? (c) What is the value of int_(-a)^(a) f(x) dx? (d) Has y = f(x) point of inflection? (e) What is the nature of y = f(x)? Monotonic or non-monotonic? |
|
Answer» Solution :(a) The graph ofy = f'(x) is symmetrical about the y-axis, so f(x) is an even FUNCTION. (b) f(0) = 0, so f(x) is an odd function [derivative of an odd function is even]. (c) Asf(x) is odd, so `UNDERSET(-a)overset(a) int f(x) dx = 0` (d) `f''(x) gt 0 as x lt 0 and f''(x) lt 0 "as " x gt 0`. THEREFORE, x = 0 is the point of INFLEXION. (e) ` f'(x) le 0, forallx,` so f(x) is always decreasing. |
|
| 1337. |
If a line is perpendicular to z-axis and makes an angle measuring 60^0 with x-axis, then the angle it makes with y-axis measures_____. |
|
Answer» `30^0` |
|
| 1338. |
If (3,0) is the focus and y axis is the tangent at vertex. Then the equation of the parabola is |
|
Answer» `x^2 = 12X` |
|
| 1339. |
Let 4x^(2)-4(alpha-2)x + alpha-2=0(alpha in R) be a quadratic equation. Find the values of alpha for whichAtleast one root lies in (0, (1)/(2)) |
|
Answer» |
|
| 1341. |
The values of p and q for which the function f(x)={{:(,(sin(p+1)x+sinx)/(x),x lt 0),(,(qroot(x+x^(2))-sqrtx)/(x^(3//2)),x gt 0):} is continuous for all x in R, are |
|
Answer» `p=3/2,q=1/2` |
|
| 1342. |
Let A(4,3),B(-4,3) and C(0,-5) be the vertices of triangle and P(5,0) let L,M and N be the feet of the perpendiculars drawn from P onto the sides BC,CA and AB respectively then |
|
Answer» <P>area of `Delta LMN` is 5 sq. units So `L,M,N` are collinear (i.e. Simson's line) |
|
| 1343. |
Given eight distinguishable rings, the number of possible five ring arrangements on the four fingers (not the thumb) of one hand is (the order of the rings on each finger is significant, but it not required that such that each finger have a ring) is |
|
Answer» `.^(8)C_(5)xx4^(5)` |
|
| 1344. |
Integrate the following functions sqrt(x^2+4x+1) |
|
Answer» SOLUTION :`INT SQRT(x^2+4x+1) DX` =`int sqrt(x^2+4x+4-(sqrt3)^2) dx` =`int sqrt((x+2)^2-(sqrt3)^2) dx` `(x+2)/2 sqrt((x+2)-(sqrt3)^2-(sqrt)^2/2 log|x+2+sqrt(x^2+4x+1)|+c` =`(x+2)/2 sqrt(x^2+4x+1)-3/2 log|x+2+sqrt(x^2+4x=1)|+c` |
|
| 1345. |
The solution of(x^(2) y^(3) + x^(2)) + (y^(2) x^(3) + y^(2)) dy = 0 is |
|
Answer» `(X^(3) + 1) (y^(3) + 1) = C` |
|
| 1346. |
Write the number of solution of the following system of equation. x-2y=0 |
| Answer» SOLUTION :INFINITE | |
| 1347. |
The region M consists of all the points (x, y) satisfying the inequalities y ge 0, y lex and yle 2 - x. The region N which varies with the parameter t consists of all points which satisfy tle xlet + 1 AAt in [0, 1], then min(ar(M cap N)) is |
|
Answer» `1/2` SQ. UNITS |
|
| 1348. |
A (-1,2-3), B(5,0,-6), C(0,4,-1) are three points, Show that direction cosines of the bisectors oflfloorBAC are proportional to (25,8,5)and (-11,20,23). |
|
Answer» |
|
| 1349. |
Let the nine different lettersA, B, C… I in {1, 2, 3, …, 9}. Then find the probability that product (A - 1)(B - 1) … (I - 9) is an even number. |
|
Answer» `THEREFORE` Required probability = 1 |
|
| 1350. |
Find the general value of sin^-1(sqrt3/2) |
| Answer» | |