InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 1901. |
The parabola with drectrix x+2y-1=0 and focus (1,0) is |
|
Answer» `4X^(2)-4xy+y^(2)-8x+4y+4=0` |
|
| 1902. |
Show that if A and B are square matrics such that AB=BA , then (A+B)^(2)=A^(2)+2AB+B^(2). |
|
Answer» |
|
| 1903. |
If A=[{:(8,0),(4,-2),(3,6):}]andB=[{:(2,-2),(4,2),(-5,1):}], then find the matrix X , such that 2A+3X=5B. |
|
Answer» |
|
| 1904. |
If a gt b and e is the eccentricity of the ellipsethen the equation of the normal at the end of the latusrectum in the first quadrant is |
|
Answer» `x-ey+ae^(3)=0` |
|
| 1905. |
If S = 0, S' =0 are two touching circles then angle between their radical axis and the common tangent at the at their points of contanct is |
|
Answer» `30^@` |
|
| 1906. |
Evalute the following integrals int (cos 6x- cos 4x)/(sin 6x - sin 4x) dx |
|
Answer» |
|
| 1907. |
Three vertices of a rectangle are (3,2),(-4,2) and (-4,5). Plot the points and find the coordinates of thefourth vertex. |
|
Answer» `(-1,13,13)` |
|
| 1908. |
Construct truth tables for the following and indicate which of these are tautologies (p rarr ~~p) rarr~~p |
Answer» SOLUTION :
|
|
| 1909. |
Let f: R be a function. We say that f has PROPERTY 2 if lim_(hto0)(f(h)-f(0))/(h^2) exists and is finite. Then which of the following options is/are correct ? |
|
Answer» `f(x)=sinx` has PROPERTY 2 property 2, `underset(hto0)(lim)(f(h)-(f(0)))/(h^(2))` exists and finite. OPTION a, `P2:underset(hto0)(lim)(h^(2//3)-0)/(sqrt(|h|))=underset(hto0)(lim)(1)/(h)((sinh)/(h))=`doesn't exist. option b, `P1:underset(hto0)(lim)(|h|-0)/(sqrt(|h|))=underset(hto0)(lim)(|h|)/(h)={{:(1,"if "hto0^(+)),(-1," if "hto0^(-)):}` so `underset(hto0)(lim)(f(h)-f(0))/(h^(2))` does not exist. |
|
| 1910. |
If the coefficients of variation of two distributions are 40 and 20 and their variances are 144 and 64 respectively, then the mean of their arithmetic means is |
|
Answer» 40 |
|
| 1911. |
If2,3 aretworootsofthereciprocalequation6x^5 - 29 x^4 +2x^3 +2x^2 -29 x+6=0 thenthe otherrootsare |
|
Answer» `1,-2,3` |
|
| 1912. |
If int (f(x)dx)/(log sin x)= log sin x, then f(x)=.... |
| Answer» Answer :D | |
| 1913. |
If two dice are rolled then the probability of getting both even or sum 10 is |
|
Answer» `(4)/(18)` |
|
| 1914. |
If there are 25 railway stations on a railway line, how many types of single second class tickets must be printed, so as to enable a passenger to travel from one station to another. |
|
Answer» |
|
| 1915. |
A particle P moves on the line y=x, xle0 with constant speed u m//sec. Another particle Q revolves along the circke (x-1)^(2)+y^(2)=1/9 with constant speed (omega)/3m//sec. In anticlockwise directio, let at t=0, both P and Q simultaeously started, P from the point (0,0) and Q from he point (2/3,0). Further at any time instant t sec, let the distance of theri separation is r(t)m. Also it was observed that at time t_(0) sec, both P and Q are at their closest distance of approach, denoted by r_("minimum")m, then choose the correct statements from among the following |
|
Answer» <P>`[12r_("minimum")]=4` (where [.] denotes the greatest integer function) `y=-x+1,(x-1)^(2)+y^(2)=1/3` `x+y-1=0,2y^(2)=1/9` `x-1=y,y^(2)=1/(3sqrt(2))` 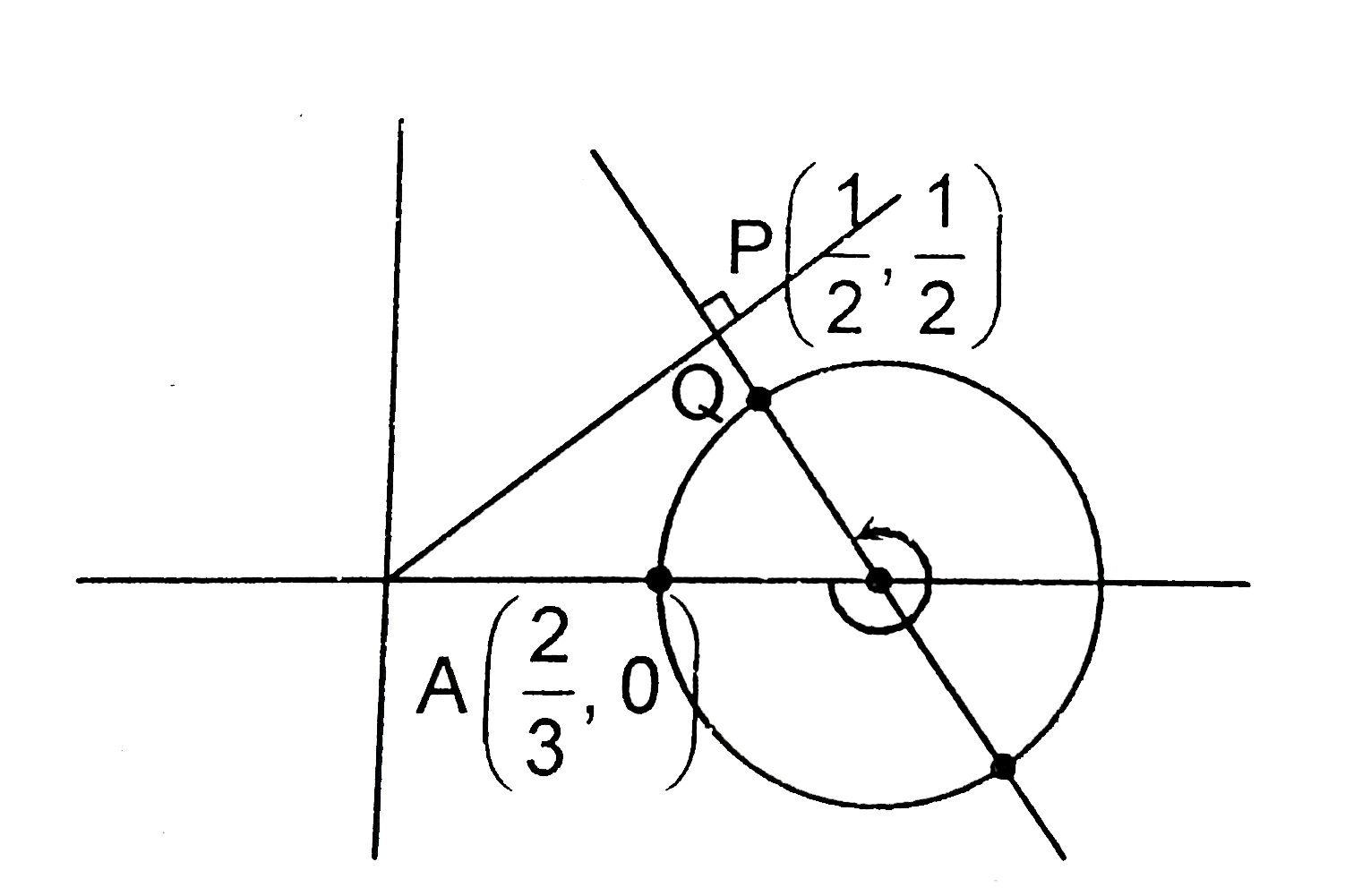 Clearly SHORTEST distance of approach is along common normal whose equation is `x+y=1=0`. So, when they are at their CLOSEST distance `P` must be at `(1/2,1/2)` and `Q` must be at `(1- 1/(3sqrt(2)),1/(3sqrt(2)))` covering angle `(7pi)/4` on the circle . Since `P` and `Q` happened to be at these points at same time so we have `t_(0)=(7pi)/(4w)=1/(sqrt(2u))` also at this instance `t_(0),r_("min")=(3-sqrt(2))/(3sqrt(2))IMPLIES[12r_("min")]=[6sqrt(2)-4]=4` Also at any time instant `t_(1)` co-ordinate of `P,Q` are `((ut)/(sqrt(2)),(ut)/(sqrt(2)))` at `Q(1+(cos(omegat))/3,+sin((omegat)/3))` `:.r^(2)(t)=((ut)/(sqrt(2))-1 - (cos(omegat))/3)^(2)+((ut)/(sqrt(2))-(sin(omegat))/3)^(2)` |
|
| 1916. |
If omegane1 is a cube root ofunity, then the sum of the series S=1+2omega+3omega^(2)+…..+3nomega^(3n-1) is |
|
Answer» `(3N)/(omega-1)` |
|
| 1918. |
Match the items from List-I that of List-II A bag contains 4 red , 3 white and 5 blue balls. Three balls are drawn at a time randomly from the bag. The correct answer is |
|
Answer» `{:(A,B,C,D),(v,II, iii, IV):}` |
|
| 1919. |
If veca=3hati-hatj+2hatk and vecb=hati-3hatk then veca.vecb is |
|
Answer» 3 |
|
| 1920. |
f(x)= {(3x-8,"If " x le 5),(2k,"if" x gt 5):} is continuous, find k |
| Answer» Answer :A | |
| 1921. |
Integrate the following functions : tan^(-1)(sqrtx) |
|
Answer» |
|
| 1922. |
Pulmonary surfactant is :- |
|
Answer» AMINO acid |
|
| 1923. |
If(2x ^ 3+x ^ 2- 5 ) /( x ^4-25 )=(Ax +B)/( x ^ 2- 5 )+(Cx + 1 ) /( x ^ 2+5 ),then(A, B, C)equalsto |
|
Answer» ` (1, 1, 1 ) ` ` rArr(Ax + B )(x ^ 2+5 )+(x + 1 )(x ^ 2- 5 )=2X ^ 3+x ^ 2- 5 ` ` rArr A + C = 2 , 5B - 5 =- 5 ` ` 5A - 5C =0 rArr B =0 ` ` rArrA = C ` `thereforeA = C = 1` `therefore( A, B, C )=(1, 0, 1 ) ` |
|
| 1925. |
Only 3 students A, B, C appear at a competetive examination. The probability of A coming first isthree times that of B and the probaility of B coming first is 3 times that of C. Find the probability of each coming first. |
|
Answer» |
|
| 1926. |
If the lines barr = (2, -3, 7) + k(2, a, 5), k epsilon Rand barr = (1, 2, 3) + k(3, -a, a), k epsilon R are perpendicular to each other then a = ...... |
|
Answer» 2 |
|
| 1927. |
If Arg (3z-2i) = pi//2 then the locus of z = x +iy is |
|
Answer» `x^(2) + y^(2) - 3x - 2 = 0 , y = 0` |
|
| 1928. |
Match theequationgiven in List - I to the curve, it represents on Argand plane, given in List - II (Here z is a complex number and omega is a non real cube root of unity) |
|
Answer» `{:(P, Q, R, S),(4, 1, 2, 3):}` |
|
| 1929. |
If 3 cards are drawn from a pack of 52 cards at random, then the probability of getting cards from one suit and one card from another suit is |
|
Answer» <P>`(.^(4)C_(2)XX.^(13)C_(2)xx.^(13)C_(1))/(.^(52)C_(3))` |
|
| 1930. |
The pH of the water in Lake Michigan was tested at 13 locations along the illions shoreline. The data is presented in the scatterplot above. Which of the following best represents the mode of the pH in the collected data? |
|
Answer» 7.2 |
|
| 1931. |
Evaluate : int(x^(2) sin^(-1)x)/((1-x^(2))^((3)/(2)))dx |
|
Answer» |
|
| 1932. |
If x^(a)*(x^(a+1))^(a)*(x^(a))^(1-a)=x^(k), then k= |
| Answer» SOLUTION :`X^(a)*x^(a^(2)+a)*x^(a-a^(2))=x^(a+a^(2)+a+a-a^(2)=x^(3a))`. | |
| 1933. |
The relation R defined in the set of real number R is as follow : R {(x,y) : x - y + sqrt2 is an irrational number} Is R transitive relation ? |
|
Answer» |
|
| 1934. |
Assume int _(0) ^(pi) ln sin theta d theta =- pi ln 2then prove that int _(0) ^(pi) theta ^(3) ln sin theta d theta =(3pi)/(2) int_(0) ^(pi) theta ^(2) ln ( sqrt2 sin theta) d theta. |
|
Answer» |
|
| 1935. |
Using L' Hospital' s rule prove that lim_(x to (pi)/(2)) (sec x - tan x ) = 0 |
|
Answer» |
|
| 1936. |
If f(x)=2x^(4)-13x^(2)+ax+b is divisible by x^(2)-3x+2, then (a, b) is equal to |
| Answer» ANSWER :C | |
| 1937. |
Write{x:x =can be written as a sum of two odd integers } set in the form of lists? |
| Answer» SOLUTION :`{2,4,6,8,10,………}` | |
| 1938. |
If Delta_(1)=|(x,b,b),(a,x,b),(a,a,x)|" and "Delta_(2)=|(x,b),(a,x)|, then |
|
Answer» `Delta_(1)=3(Delta_(2))^(2)` `(1)/(a)+(1)/(ar)+(1)/(ar^(2))+(1)/(ar^(3))+(1)/(ar^(4))=10implies(1)/(a^(2)R^(4))(a+ar+ar^(2)+ar^(3)+ar^(4))=10impliesa^(2)r^(4)=4impliesar^(2)=pm2` `|S|=|a^(5).r^(10)|=|(pm2)^(5)|` |
|
| 1940. |
If f(x) is a polynomial of degree m(ge1), then which of the following is not true ? |
|
Answer» `(d^(n)y)/(dx^(n))=0`, for all `NGTM` |
|
| 1941. |
If the normals from any point to the parabola x^(2)=4y cuts the line y=2 in points whose abscissae are in A.P., then the slope of the tangents at the 3 conormal points are in |
|
Answer» AP |
|
| 1942. |
Match the following {:("Line", "Intercepts"),(I. 3x+4y=6, (a) -13//2","-13//3),(II. 5x-2y+10=0, (b)5"," 5//3),(III."joining the points (2, -1), (-1, 2)", (c) -2","5),(IV."Joining the points (4, -7), (1, -5)", (d) 2"," 3//2):} |
|
Answer» C, d, a, B |
|
| 1943. |
State which of the following statement is true? |
|
Answer» If `y^(2)=x` then y amy be regarded as a FUNCTION of x . |
|
| 1944. |
Let P and Q be two sets defined as follows: P-{z sub C :(1 +i)z ge 0} Q = {z in C, z/(1+i) ge 0}, then |
|
Answer» <P>P = Q |
|
| 1945. |
If a matrix has 5 elements, what are the possible orders it can have? |
|
Answer» |
|
| 1946. |
Find the shortest distance vecr=hati+2hatj+3hatk+lambda(hati-3hatj+2hatk)and vecr=4hati+5hatj+6hatk+mu(2hati+3hatj+hatk). |
|
Answer» |
|
| 1947. |
tan ^(-1) "" (1)/(2)+ tan ^(-1) "" (2)/(11) = tan ^(-1)""(3)/(4) |
|
Answer» |
|
| 1948. |
Ifveca , vec ball are unit vector, then the greatest value of|veca +vecb| + |veca-vecb| is |
| Answer» Answer :A | |
| 1950. |
An infinite G.P has first 13 term as a and sum 5 , then |
|
Answer» `a LT - 10` |
|