Explore topic-wise InterviewSolutions in .

This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.

1801.

The seriesof naturalnumbers is divided into groups(1),(2,3,4) : (5,6,7,8,9) and soon . Show the sum of the numbersin the nth groupis (n-1)^(3) +n^(3)

Answer»


ANSWER :1275
Discussion
1802.

The value ofSigma_(n=1)^(infty) cot^(-1) ( n^(2) + n +1) is also equal to

Answer»

`cot^(-1)(-1)+sec^(-1)(1)- COSEC^(-1)(1)`
`cot^(-1)(2) + cot^(-1)(3)`
minimum value of the function `f(x) = TAN^(-1) ((1-x^(2))/(1+x^(2)))`
`COS^(-1)(cos 41 pi/4)`

Answer :A::B::D
Discussion
1803.

Evaluate the following integrals int (2-3 sinx)/cos^2x dx

Answer»

SOLUTION :`INT ((2-3SINX)/cos^2x)DX = int(2/cos^2x -(3sinx)/cos^2x)dx = int(2 sec^2x- 3secxtanx)dx =2tanx-3secx+c`
Discussion
1804.

int(cos6x-cos4x)/(sin6x-sin4x)

Answer»


ANSWER :`(1)/(5)log|cos5x|+c`
Discussion
1805.

A companymanufactureis bicyles and tricycleseach of whichmust beprocessed through machines A and B. Machine A hasmaximum of 120 hoursavaiableand machine B hasmaximumof 180 hours available hourson machine A and 3 hourson machine B. Machine A and 10 hourson machine B.Ifprofitare ₹ 180 for a bicyleand ₹ 220 for a tricyle , formulateand solvethe L.P.P to determinethenumberof bicyclesand tricycle that should bemanufactured in orderto maximize the profit .

Answer»

Solution :Let x no. of bicyclesand y no.oftricycleare to be manufactured . Then, total profit Z = (180 x+ 220 y) WHICHIS to bemaximized.

From table, we have
`6X + 4y le 120 , 3x + 10y le 180`
` x ge 0 ,y ge 0`
(`because` no . ofbicycles and tricyles cannot be negative)
Themathematicalformulation of given LPP is
Maximie Z = 180 x + 220y
such that`6x + 4yle 120,`
`3x + 10y le 180`
`x ge 0 , y ge 0`
Now , darw the LINE AB and CD of equations `6x4y = 120` and `3x + 10y = 180` respectively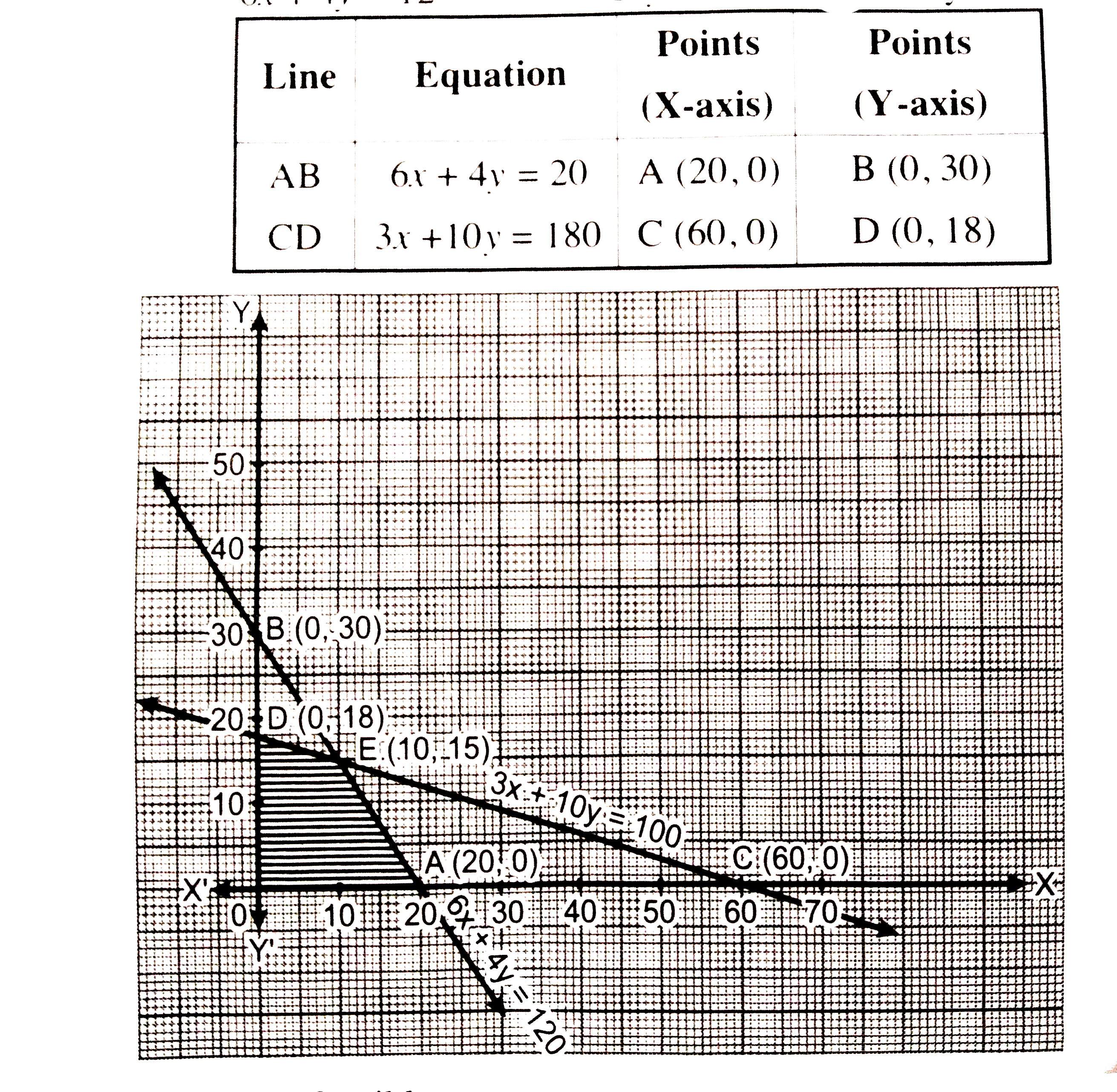

Thefeasibleregion is OAEDO with`O(0,0), A(20,0) E and D (0,18)`
E is thepointof intersectionof thelines.
`""3x + 10y = 180,"".......(1)`
`and""6x + 4y = 120 "".....(2)`
Multiplying EQUATION (1) by 2 andsubtracting equation (2) form it , we get
`{:(6x + 20y = 360),(6x + 4y = 120),(-" "-" "-),(overline(""16y = 240)):}`
`rArr "y = 15`
Puttingy= 15 in equation (1), we get x = 10
`therefore E(10, 15)`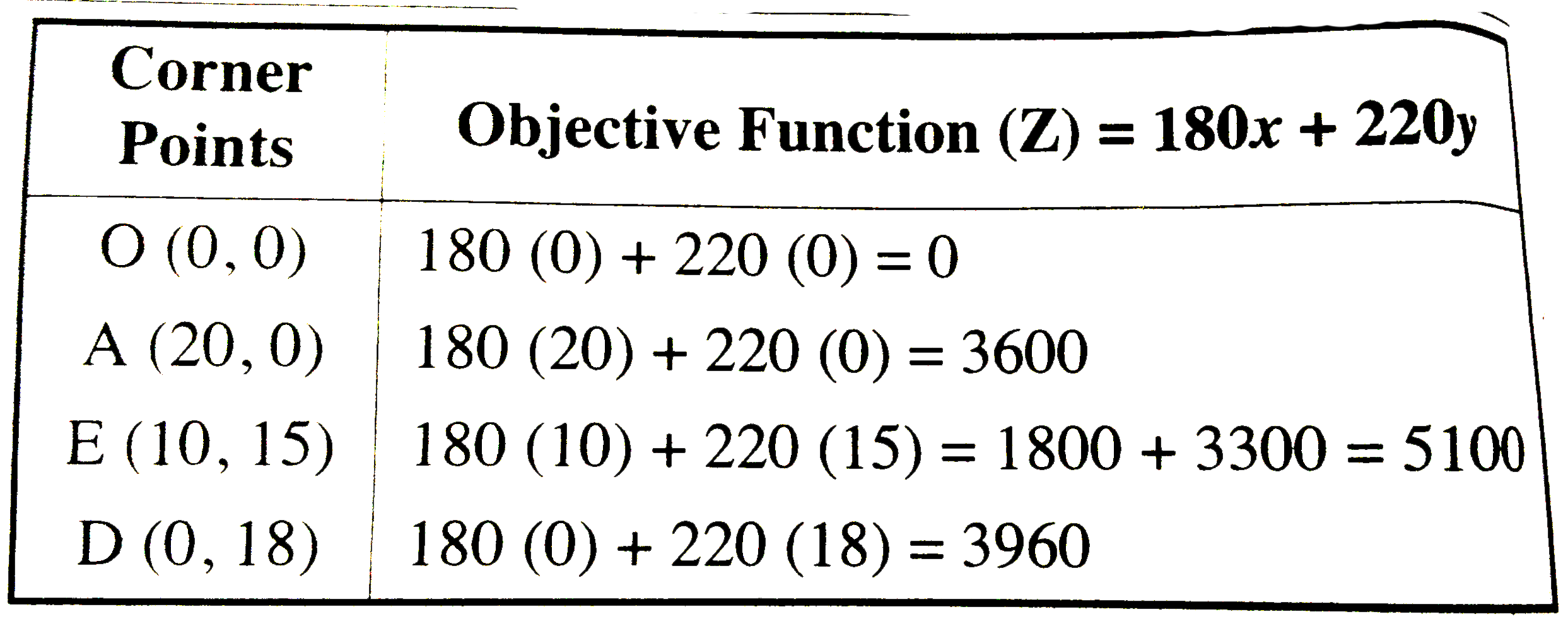

HENCE, the maximum valueof Z is5100 at E (10, 15) i.e.,10 bicyles and15 tricylesshouldbe manufactured to maximize the profit.
Discussion
1806.

10% items are defective manufactured by one company. Find the probability of an event that out of 8 items 2 items are defective.

Answer»


ANSWER :`(28 XX 9^(6))/(10^(8))`
Discussion
1807.

A shopkeeper sells not more than 15 bush shirts of two colours. At least twice as many white ones are sold as green ones. If the profit on each of the white be Rs. 5 and that of green be Rs. 7.50. The numbers of green shirts to be sold to get maximum profit is

Answer»

5
7
10
15

Answer :C
Discussion
1808.

A round table of radius 10 m has four vertical legs fixed at the circumference of the table top in the form of four corners of a square. If the mass of the table is 10 kg, what maximum mass (in kg) can be kept on the circumference of the table so that table doesn't topple is (x/(sqrt(2)-y)), then the value of (x+y) is ?

Answer»


ANSWER :`40.0`
Discussion
1809.

h(x) is increasing for x in

Answer»

`(-(pi)/(4),(pi)/(4))`
`(-(pi)/(2),-(pi)/(4))uu(pi)/(4),(pi)/(2))`
`(-(pi)/(4),0)uu(pi)/(4),(pi)/(2))`
`(-(pi)/(2),-(pi)/(4))uu(0,(pi)/(4))`

Solution :h(x) is increasing `rArr h'(x)GT0`
CASE I
`{:("(i) "sin 2x gt0 rArr x in (0,(pi)/(2))),("(ii) "f'(sin^(2)x)gtf'(cos^(2)x) rArr tan^(2)x GT1):}}rArr x in ((pi)/(4),(pi)/(2))`
Case II
`{:(" (i)" sin2xlt0 rArr x in (-(pi)/(2)","0)),(" (ii)"f'(sin^(2)x)gtf'(cos^(2)x) rArr tan^(2)xgt1):}}rArr x in ((-pi)/(2),-(pi)/(4))`
Discussion
1810.

int_(0)^(sqrt(e)) x log x dx

Answer»


ANSWER :0
Discussion
1811.

The value of the sum .^(1000)C_(50) + .^(999)C_(49) +.^(998)C_(48)+"….".^(950)C_(0) is

Answer»

`.^(1001)C_(50)`
`.^(1002)C_(951)`
`.^(1001)C_(950)`
`.^(1002)C_(50)`

Solution :`.^(1000)C_(50)+.^(999)C_(49)+.^(998)C_(48)+"...."+.^(950)C_(0)`
`=` coefficient of `x^(950)` in `[(1+x)^(950) + (1+x)^(951) + "....."+(1+x)^(1000)]`
`=` coefficientof `x^(950)` in `((1+x)^(950)((1+x)^(51)-1))/((1+x)-1)`
`=` coefficient of `x^(950)` in `((1+x)^(1001) - (1+x)^(950))/(x)`
`=` coefficient of `x^(951)` in `(1+x)^(1001)`
`= .^(1001)C_(1951) = .^(1001)C_(50)`
Discussion
1812.

Evaluate the following integrals int_0^(pi/2)(cosx-sinx)dx

Answer»

Solution :`int_0^(pi/2)(cosx-sinx)DX=[sinx+cosx]_0^(pi/2)`
`(SIN(pi/2)-SIN0)+(COS(pi/2)-cos0)=1-1=0`
Discussion
1813.

If , then value of X^(n) is (where n is a natural number)

Answer»

`{:[(,3N,-4),(,N,-n)]:}`
`{:[(,2n+n,5-n),(,n,-n)]:}`
`{:[(,3^(n),(-4)^(n)),(,1^(n),(-1)^(n))]:}`
`{:[(,2n+1,-4),(,n,-(2n-1))]:}`

Answer :D
Discussion
1814.

If a, b and c are real numbers , and Delta=|{:(b+c,c+a,a+b),(c+a,a+b,b+c),(a+b,b+c,c+a):}| Show that either a+b+c=0 or a=b=c

Answer»


ANSWER :`thereforea+b+c=0" or " a=b=c`
Discussion
1815.

If the direction cosines of two lines are such that l+m - n = 0 , l^(2)+m^(2)-n^(2)=0 thenthe angle between them is

Answer»

`PI`
`pi/3`
`pi/4`
`pi/6`

ANSWER :B
Discussion
1816.

The probability of a bomb hitting a bridge is (1)/(2) and three direct is hits (not necessarily consecutives) are neededto destroyit. Find the minimum number of bombs required so that the probability of the bridge being destroyed is greater than 0.9.

Answer»


ANSWER :9
Discussion
1817.

Let f(x)be a derivable function, f'(x) gt f(x) and f(0)=0. Then

Answer»

`F(X) gt 0" for all " x gt 0`
`f(x) lt 0" for all " x gt 0`
no sign of f(x) can be ascertained
f(x) is a constant function

Answer :A
Discussion
1818.

If 3A-B=[(5,0),(1,1)] and B=[(4,3),(2,5)] the find the matrix A.

Answer»


ANSWER :`[(3,1),(1,2)]`
Discussion
1819.

int (tanx)/(sqrt(a+b tan^(2)x))dx=

Answer»

`(1)/(sqrt(B-a))COS^(-1)[sqrt((b-a)/(b))COSX]+C`
`-(1)/(sqrt(b-a))Cos^(-1)[sqrt((b-a)/(b))cosx]+c`
`(2)/(sqrt(b-a))Cos^(-1)[sqrt((b-a)/(b))cosx]+c`
`-(2)/(sqrt(b-a))Cos^(-1)[sqrt((b-a)/(b))cosx]+c`

Answer :1
Discussion
1820.

Coordinates of the point on the parabola y^(2)=8x which is at minimum distance from the circle x^(2)+(y+6)^(2)=1 is

Answer»

`(2,-4)`
`(2,4)`
`(18,-12)`
None of these

Solution :Ellipses centred a ORIGIN are given by `(x^(2))/(a^(2))+(y^(2))/(b^(2))=1`
where a and b are unknown constant.
`(2x)/(a^(2))+(2y)/(b^(2))y_(1)=0implies (x)/(a^(2))+(y)/(b^(2))y_(1)=0`
Differentiating again, we have
`(1)/(a^(2))+(1)/(b^(2))(y_(1)^(2)+yy_(2))=0`
Multiplying `( iii )` with `x` and then subtracting from `( ii )` , we have
`(1//b)^(2)(yy_(1)-xy_(1)^(2)-xyy_(2))=0impliesxyy_(2)+xy_(1)^(2)-yy_(1)=0`
Discussion
1821.

Match the following lists :

Answer»

SOLUTION :`ararrp, brarrq, r, crarrs, r,drarrq,r.`
a. `f(1-X)=f(1+x)`
`therefore""-f'(1-x)=f'(1+x)`
Hence, graph of f(x) is SYMMETRICAL about point (1, 0) [ as if f(x) = - f(-x), then f(x) is odd and its graphs is symmetrical about (0,0). Now shift the graph at (1,0)].
b. `f(2-x)+f(x)=0`
`"Replace" x by 1+x. Then f(2-(1+x))+f(1+x)=0`
`"or "f(1-x)+f(1+x)=0`
`"or "-f'(1-x)+f'(1+x)=0`
`"or "f'(1-x)=f'(1+x)"(1)"`
Therefore, graph of f'(x) is symmetrical about line x=1.
Alos, put x=2 in (1). Then f'(-1)=f'(3).
c. `f(x+2)+f(x)=0"(1)"`
Replace `x by x + 2. then f(x+4)+g(c+2)=0"(2)"`
From (1) and (2), we have f(x) = f(x+4)
Hence, f(x) is periodic with period 4.
Also, f'(x)=f'(x+4).
Hence, f'(x) is periodic with period 4.
Put `=-1 in f'(x)=f'(x+4). Then f'(-1)=f'(3)`.
d. `"Putting "x=0, y = 0, we GET 2f(0)+{f(0)}^(2)=1`
`"or "f(0)=sqrt(2)-1""[because f(0)gt0]`
Putting `y=x, 2f(x)+{f(x)}^(2)=1`
Differentiating w.r.t. x, we get
`2f'(x)+2fcdotf'(x)=0`
`"or "f'(x){1+f(x)}=0`
`"or "f'(x)=0," because "f(x)gt0`.
Discussion
1822.

Match the following lists :

Answer»

Solution :`ararrq,brarrr,drarrp.`
a. `(dy)/(dx)=(dy//dt)/(dx//dt)=(12t^(2)-6t-18)/(5t^(4)-15t^(2)-20)`
`"or "(dy)/(dx):|_(t=1)=(12-6-18)/(5-15-20)=(2)/(5)`
`"or "-5(dy)/(dx):|_(t=1)=-2" at "t=1`
B. Let us take
`P(x)=a(x-2)^(4)+b(x-2)^(3)+c(x-2)^(2)+d(x-2)-1`
`therefore""P(2)=-1`
`0=P'(2)=d`
`2=P''(2)=2 c or c=1`
`-12=P'''(2)=6 b or b=-2`
`24=P^(iv)(2)=24a or a=1`
Thus, `P''(x)=12 (x-2)^(2)-12(x-2)+2`
`"or "P''(3)=12-12(1)+2=2`
c. `"Here, "sqrt((1+y^(4)))=sqrt((1+(1)/(x^(4))))=(sqrt(1+x^(4)))/(x^(2))""(becausey=(1)/(x))`
`"or "(sqrt(1+y^(4)))/(sqrt(1+x^(4)))=(1)/(x^(2))"(1)"`
`"But "y=(1)/(x)`
`therefore""(dy)/(dx)=-(1)/(x^(2))"(2)"`
`"From (1) and (2), "(sqrt(1+y^(4)))/(sqrt(1+x^(4)))=-(dy)/(dx)`
`"or "((dy)/sqrt(1+y^(4)))/((dx)/sqrt(1+x^(4)))=-1`
d. Obviously, f(x) is a linear function.
Also, from f'(0) = p and f(0) = Q, f(x) = px +q
`"or "f''(0)=0`
Discussion
1823.

Match the following lists :

Answer»

Solution :`ararrq,r,brarrp,r,s,crarrq,s,drarrq,r.`
a. We know that
`2tan^(-1)x={{:(sin^(-1)((2x)/(1+x^(2)))",",if -1lexle1),(pi-sin^(-1)((2x)/(1+x^(2)))",",if xgt 1),(-pi-sin^(-1)((2x)/(1+x^(2)))",", if x lt -1):}`
`"or "(dy)/(dx)=-(2)/(1+x^(2))if x lt -1 or x GT 1`
b. `cos^(-1)((1)/(sqrt(1+x^(2))))={{:(tan^(-1)x",", XGE0),(-tan^(-1)x",",x lt0):}`
`"or "(dy)/(dx)=-(1)/(1+x^(2))if x lt 0`
c. `y=|E|^(|x|)-e|={{:(|e^(x)-e|",", xge0),(|e^(-x)-e|",", xlt0):}={{:(e^(x)-e",",x ge 1),(e-e^(x)",", 0lt x lt 1),(e-e^(-x)",", -1 le x lt 0),(e^(-x)-e",", x lt-1):}`
`"or "(dy)/(dx)gt0if x gt or -1 lt x lt 0.`
d. `u=log |2x|, y=|tan^(-1)x|`
`"or "(du)/(dx)=(1)/(x)and (dv)/(dx)={{:((1)/(1+x^(2))",",x gt0),(-(1)/(1+x^(2))",", xlt 0):}`
`therefore" " (dv)/(dv)={{:((1)/(1+x^(2))",",x gt0),(-(1)/(1+x^(2))",", xlt 0):}`
Now, we know that
`(1+x^(2))/(x)=x+(1)/(x)gt2 if x gt1 and lt -2 if x lt -1`
`therefore""(du)/(dv)gt2 if xlt-1 or xgt1`
Discussion
1824.

If ""^(n)C_(5)=""^(n)C_(6) then find the value of ""^(13)C_(n).

Answer»


ANSWER :78
Discussion
1825.

The circle x^2 + y^2 - 8x + 4y + 4 = 0 toches

Answer»

`(2, -1)`
`(2,1)`
NONE of these
`(SQRT(2) , 1)`

ANSWER :A
Discussion
1826.

Find x, if [(x, -5, -1)][(1,0,2),(0,2,1),(2,0,3)][(x),(4),(1)]=O

Answer»


ANSWER :`x=pm 4sqrt(3)`
Discussion
1827.

If the foot of perpendicular drawn from the origin to a plane is (5, - 3, - 2), then the equation of plane is barr.(5bari-3barj-2bark)=38.

Answer»


ANSWER :A
Discussion
1828.

The plane makes the angles (pi)/(4),(pi)/(4) and (pi)/(2) with the positive direction of X - axis, Y - axis and Z- axis respectively. The length of perpendicular drawn from origin to the plane is sqrt(2) , then the equation of the plane is .......

Answer»

X+y = 2
x+y+z = 1
x+y+z = `SQRT(2)`
`x = sqrt(2)`

ANSWER :A
Discussion
1829.

int_(a)^(b) (|x-a|+|x-b|)dx(0 lt a lt b)=

Answer»

`(b-a)^(2)`
`(b-a)`
`b+a`
`(b+a)^(2)`

ANSWER :A
Discussion
1830.

If the vector vec(b) is collinear to the vector bar(a) and bar(a)=(2sqrt(2),-1,4) and |vec(b)|=10 then ……………

Answer»

`a +- b=0`
`a+-2b=0`
`2a+-b=0`
NONE of these

ANSWER :C
Discussion
1831.

The value oflim_(n to oo )1/n^(3)sum_(k =1)^(n)( k^(2)x ) is

Answer»

X
`x/2 `
`x/3 `
`x/4 `

ANSWER :C
Discussion
1832.

Which of the following alkanes will have the lowest biling point ?

Answer»




SOLUTION :NA
Discussion
1833.

Consider a parabola y ^(2) = alpha x anda point (- (alpha )/(4), 0) then midpoint of centres of the circles touching the tangents from given point and its chord of contact is

Answer»

`ALPHA /2`
`alpha /4`
`(3alpha )/(2)`
NONE of these

ANSWER :D
Discussion
1834.

Statement-1(Assertion and Statement -2 (reason) Each of these examples also has four alternative choices, only one of which is the correct answer. You have selectthe correct choice as given below. Statement-1 If p,qinN satisfy the equation x^sqrtx=(sqrtx)^xand qgtp, then q is a perfect number . ,ltbgtIf a number is equal to the sum of its factor, then number is known as perfect number.

Answer»

STATEMENT -1 if TRUE, Statement-2 is true, Statement-2 is a CORRECT explanation for Statement -2
Statement -1 if true, Statement-2 is true, Statement-2 is not a correct explanation for Statement -2
Statement -1 if true, Statement-2 is false
Statement -1 if false , Statement-2 is true

Answer :D
Discussion
1835.

int_(0)^(pi)|cosx|dx=.......... .

Answer»

2
1
0
`-1`

ANSWER :A
Discussion
1836.

Find the area enclosed betweent the curve y = x^(2)+3, y = 0, x = - 1, x = 2.

Answer»


SOLUTION :N//A
Discussion
1837.

Which of the following statement is true :-

Answer»

`~(pharr~q)` is TAUTOLOGY
`~(pharr~q)` is EQUIVALENT to `PHARRQ`
`(p^^~q)` is a FALLACY
`(p^^~q)^^(~p^^q)` is a tautology

SOLUTION :
Discussion
1838.

Evaluate the following integrals. int(ax^(n-1))/(bx^(n)+c)dx

Answer»


Answer :`(a)/(NB) LOG |bx^(N) + C| + k `
Discussion
1839.

A coin whose faces are marked 3 and 5 is tossed 4 times. The odds against the sum of the numbers thrown being less than 15 are

Answer»


ANSWER :`5 : 11`
Discussion
1840.

The solution of differential equation cos x (dy)/(dx)+y sin x =1

Answer»

`tanx+tany=k`
`tanx-tany=k`
`(tanx)/(tany)=k`
`tanx.tany=k`

Solution :Given that, `""tanysec^(2)xdx+tanxsec^(2)ydy=0`
`rArr""tansec^(2)xdx=-tanxsec^(2)ydy`
`rArr""(sec^(2)x)/(tanx)DX=(-sec^(2)y)/(tany)dy""`...(i)
On integrating both sides, we have
`""INT(sec^(2)x)/(tanx)dx=-int(sec^(2)y)/(tany)dy`
Put `tanx=t` in LHS integral, we get
`""sec^(2)xdx=dtrArrsec^(2)xdx=dt`
and `""tany=u` in RHS integral, we get
`""sec^(2)ydy=du`
On SUBSTITUTING these values in Eq. (i), we get
`""int(dt)/(t)=-int(du)/(u)`
`""logt=-logu+LOGK`
`rArr""log(t*u)=logk`
`rArr""log(tanxtany)=logk `
`rArr""tanxtany=k`
Discussion
1841.

Lines L_1 = ax +by +c = 0 and L_2 = lx + my + n = 0 intersect at the point P and make an anlge theta with each other. Find the equation of a line different from L_2 with pass through P and makes the same anlge theta with L_1.

Answer»


Answer :`2 (AL + bm) (ax + by +C) - (ax + by +c) - (a^2+b^2)(Ix +my +N) = 0`
Discussion
1842.

Let P be a point on the cirele x^(2)+y^(2)=9, Q a point on the line and the Pendicular bisecior of PQ be the line x-y+1=0. Then the coordinate of P are

Answer»

(3,0)
(0,3)
(72/25,-21/25)
(72/25,21/25)

ANSWER :A
Discussion
1843.

If one root of the equation x^(2) + px + q = 0 is the square of the other, then p^(3) + q^(3) =

Answer»

Q(3P + 1)
-q(3p + 1)
q(3p - 1)
q(1-3p)

ANSWER :C
Discussion
1844.

Solve the following equations (i) tan^(-1). ( x-1)/(x - 2) = tan ^(-1). ( x+1)/(x + 2)= pi/4 (ii)tan^(-1) 2 xx tan^(-1) 3x = pi/4

Answer»


ANSWER :` X = - 1 " as " x in ( - 1/sqrt6 , 1/sqrt6)`
Discussion
1845.

Assertion (A) : x + x^(2)/(1!) + x^(3) /(2!) + (x^4)/(3!) + .....+ oo = f(x) Then the series f(1), f(2) ,f(3) ,f(4)... Are in G.P . Reason (R) : In the above series f'(x) = e^(x) (x+2)

Answer»

A is TRUE, R is true and R is CORRECTEXPLANATION of A
A is true, R is true and R is not correct explanation of A
A is true , R is false
A is false, R is true

ANSWER :D
Discussion
1846.

IfDeltan=|{:(a^(2)+n,ab,ac),(ab,b^(2)+n,bc),(ac,bc,c^(2)+n):}|,n in N and the equation x^(3)-lambdax^(2)+11x-6=0 has roots a,b,c and a,b,c are in AP. The value of sum_(r=1)^(7) Delta_(n)is

Answer»

`(12)^(3)`
`(14)^(3)`
`(26)^(3)`
`(28)^(3)`

Answer :B
Discussion
1847.

IfDeltan=|{:(a^(2)+n,ab,ac),(ab,b^(2)+n,bc),(ac,bc,c^(2)+n):}|,n in N and the equation x^(3)-lambdax^(2)+11x-6=0 has roots a,b,c and a,b,c are in AP. The value of (Delta2_(n))/(Delta_(n))is

Answer»

`LT 8`
`=8`
`GT 8`
NONE of these

ANSWER :A
Discussion
1848.

Find "sin" (A)/(2) and "cos" (A)/(2) in terms of "tan"( A)/(4).

Answer»
Discussion
1849.

If lim_(x to 0) [(x(1+3acosx)- 5bsinx)/(x^3)] = 1 . The value of a and b will be

Answer»

`-5//6 , -3//10`
`-10//2 , -6//5`
`5//6 , 3//10`
`10//3 , 6//5`

ANSWER :A
Discussion
1850.

Evaluate the definite integrals int_(0)^(3)xe^(x^(2))dx

Answer»
Discussion