InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 1701. |
A vector bar( r ) is inclined at equal angles to the three axes. If the magnitude of vec( r ) is 2sqrt(3) units, then find the value of vec( r ). |
|
Answer» |
|
| 1702. |
Evaluate the following integrals int(dx)/(3-x^2) |
|
Answer» SOLUTION :`INT(dx)/(3-x^2)=int(dx)/((SQRT3)^2-x^2)` int(dx)/((sqrt3+x)(sqrt3-x))` `(1/(2sqrt3))Inabs((sqrt3+x)/(sqrt3-x))+C` |
|
| 1703. |
If three parabols touch all the lines x = 0, y = 0 and x +y =2, then maximum area of the triangle formed by joining their foci is |
|
Answer» `sqrt(3)` Hence, foci must be the VERTICES of an equilateral triangle inscribed in the circumcircle. So, area `= (sqrt(3))/(4) (sqrt(3)sqrt(2))^(2) = (3sqrt(3))/(2)`. |
|
| 1704. |
If |x| lt 1 then coefficient of x^(n) in log_(10)(1-x) is |
| Answer» Answer :B | |
| 1705. |
If edge length of an unit cell =4xx10^(-8) cm and the unit cell is a face-centered cubic with atomic mass of metal is 40 then density of the unit cell will be [N_(2)=6xx10^(23)] |
|
Answer» `(100)/(24)` gm/ml |
|
| 1706. |
When blood containing "Haemoglobin"as the colloidal partial is subjected to electro osmosis. The dispersion medium moves towards the anode. Hence, the incorrect statement will be |
|
Answer» `Fe(OH)_(3)` solution on mixing with haemoglobin in BLOOD can cause coagulation `rArr` dispersion medium has -ve charge `rArr` dispersed phase has +v charge `rArr Fe(OH)_(3)` cannot cause coagulation |
|
| 1707. |
int_(0)^(pi//4) (Tan^(n)(x-[x])+Tan^(n-2)(x-[x]))dx |
|
Answer» `(2)/(n+1)` |
|
| 1708. |
Two cards are drawn successively without replacement from a well shuffled deck of cards. Find the mean and standard variation of the random variable X, where X is the number of aces. |
|
Answer» |
|
| 1709. |
If cosec theta = (p+ q)/(p -q) , then cot ((pi)/(4) + (theta)/(2)) is equal to |
|
Answer» `SQRT ((p)/(q))` |
|
| 1710. |
The values of p and q so that the function f(x)={{:((1+|sinx|)(rho)/(sinx)",",(pi)/(6)ltx lt0),(q,", "x=0),(e^((sin2x)/(sin3x)),", "0lt x lt(pi)/(6)):} is continous at x=0 is |
|
Answer» <P>`p=(1)/(3) ,q=e^(2//3)` |
|
| 1711. |
If S, S_(1), S_(2) be the circles of radii 5, 3, 2 respectively. If S_(1) and S_(2) touch externally and they touchinternally with S. The radius of circle S_(3) which touches externally with S_(1) and S_(2) and internally with Sis : |
|
Answer» `(30)/(19)` `(r+2)^(2)+(r+3)^(2)3` `=2.3^(2)+3.2^(2)+5(5-r)^(2)` `rArr 76r = 120` `rArr r = (120)/(76)` `rArr r = (30)/(19)` 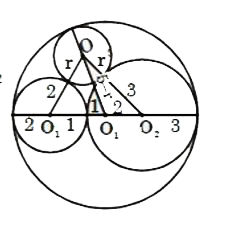
|
|
| 1712. |
Let veca, vecb and vecc be three mutually perpendicular unit vectors. If vecd is a linear combination of veca, vecb and vecc such that vecd makes equal acute angles with all three vectors veca, vecb and vecc and |vecd|=2, then the value of |veca + vecb, vecc + vecd| is |
|
Answer» `sqrt(3) +2` where `x_(1), x_(2)` and `x_(3)` are real numbers. `rArr vecd.veca = x_(1) rArr x_(1) = |vecd| cos THETA` where `theta`= angle between `vecd` and `veca` =angle between `vecd` and `vecc` Similarly `x_(2) = |vecd| cos theta` `x_(3) = |vecd| cos theta` `rArr cos^(2)theta = 1/3 rArr cos theta = 1/sqrt(3)` `|veca + vecb +vecc + vecd|^(2) = 3+4 + 6 cos theta` `=7 + 6/sqrt(3) = 7+ 2sqrt(3)` |
|
| 1713. |
[veca+2vecb-vecc,veca-vecb,veca-vecb-vecc]= |
|
Answer» 1)`2[VECA,vecb,vecc]` |
|
| 1714. |
If the data x_1,x_2,….x_10is such that the mean of four of these is 11, the mean of the remainning six is 16 and sum of squares of all these is 2000, then the standard deviations of this data is: |
| Answer» ANSWER :A | |
| 1715. |
Find the second order derivative of the following functions x^20 |
| Answer» SOLUTION :`y=x^20dy/dx=20x^19,(d^2y)/(dx^2)=20xx19xxx^18=380x^18` | |
| 1716. |
Evaluate the following define integrals as limit of sums : int_(0)^(1) (x-x^(2))dx |
|
Answer» |
|
| 1717. |
If P(A) = 0.8, P(B) = 0.5 and P (B|A) = 0.4, findP(A cap B) |
|
Answer» |
|
| 1718. |
If P=[{:(x,0,0),(0,y,0),(0,0,z):}]andQ=[{:(a,0,0),(0,b,0),(0,0,c):}], prove that PQ=[{:(xa,0,0),(0,yb,0),(0,0,zc):}]=QP. |
|
Answer» |
|
| 1719. |
Let I _(1) = int _(0) ^(1) (e ^(x) dx )/( 1 + x) and I _(2) = int _(0) ^(1) (x ^(2) dx )/(e ^(x ^(3)) (1- x ^(2))), then (I _(1))/( I _(2) is to |
| Answer» ANSWER :C | |
| 1720. |
Let f(x)="min" {x,x^(2)}("where"{x}=x-[x],"where"[x] denotes the greatest integer function ), then - |
|
Answer» f is comtinuous for all `x inRR`, |
|
| 1721. |
Let A = [{:(5,-3,0),(-3,5,0),(0,0,2):}] X be a non zero matrix of order 3xx1 and c be a real number . If A^(2)X =cAx then number of distinct values of c is |
|
Answer» 3 |
|
| 1722. |
If a chord joining P(a sec theta, a tan theta), Q(a sec alpha, a tan alpha) on the hyperbola x^(2)-y^(2) =a^(2) is the normal at P, then tan alpha = |
|
Answer» <P>`tan theta (4 sec^(2) theta+1)` `:. (tan ALPHA - tan theta)/(sec alpha - sec theta) =- (tan theta)/(sec theta)` `:. tan alpha - tan alpha =- k tantheta` and `sec alpha - sec theta = k sec theta (1+k) sec theta = sec alpha` (1) `:. (1-k) tan theta = tan alpha` (2) `[(1+k)sec theta]^(2) - [(1-k)tan theta]^(2) = sec^(2) alpha - tan^(2) alpha =1` `RARR k =- 2 (sec^(2) theta + tan^(2) theta) =- 4 sec^(2) theta +2` From (2), `tan alpha = tan theta (1+4 sec^(2) theta -2) = tan theta (4 sec^(2) theta -1)` |
|
| 1723. |
Using properties evaluate the following definite integrals int_0^(pi/2) cos^2x dx |
|
Answer» Solution :LET I = `int_0^(pi/2) cos^2 x dx` ____(a) Then I = `int_0^(pi/2) cos^2 (pi/2-x)dx` =`int_0^(pi/2) sin^2 x dx` ____(B) (a)+(b) `gt2I = int_0^(pi/2) (cos^2x+sin^2x)dx` =`int_0^(pi/2) dx = [x]_0^(pi/2) = pi/2-0 = pi/2` THUS, I = `pi/4` |
|
| 1724. |
Evalute the following integrals int (1)/(x - sqrt(x^(2) + a^(2)))dx |
|
Answer» |
|
| 1725. |
If the tangent drawn to the hyperbola (x^2)/(a^2)-(y^2)/(b^2)=1 at any point P meets the coordinate axes at the points A and B respectively. If the rectangle OACB (O being the origin) is completed, where C lies on (x^2)/(a^2)-(y^2)/(b^2)=lambda . Then, the value of lambda is: |
|
Answer» 1 |
|
| 1726. |
Assertion (A) : The origin and the roots of the equation x^(2) + ax + b = 0 form an equilateral triangle if a^(2) = 3b Reason (R) : If z_(1) , z_(2) , z_(3) are vertices of an equilateral triangle then z_(1)^(2) + z_(2)^(2) + z_(3)^(2) = z_(1) z_(2) + z_(2) z_(3) + z_(3) z_(1) |
|
Answer» Both A and R are TRUE R is correct EXPLANATION to A |
|
| 1727. |
A plane x passes through the point (1,1,1) .If b,c,a are the direction ratios of a normal to the normalto the palne , where a, b ,c (a lt b lt c) are the factors of 2001 , then the equation of the palne is |
|
Answer» `29x+31y+3Z=63` |
|
| 1728. |
find the value of given domain and express in form of logarithm function (1)/(2)-(1)/(2)*(1)/(2^(2))+(1)/(3)*(1)/(2^(3))-…….oo= |
|
Answer» `log_(e )((2)/(3))` |
|
| 1729. |
If (1 + x + x^(2))^(n) = c_(0) + c_(1) x + c_(2) x^(2) + …. ,then the value of c_(0)c_(1) - c_(1)c_(2) + c_(2)c_(3) - …… is |
| Answer» Answer :B | |
| 1730. |
If P(A) = 0.4, P(B) = 0.8, P( B | A) = 0.6 then find P( A | B) and P(A cup B). |
|
Answer» |
|
| 1731. |
The set of points on the axis of the parabola 2((x-1)^(2)+(y-1)^(2))=(x+y)^(2), from which 3 distinct normals can be drawn to the parabola, is the set of points (h, k ) lying on the axis of the parabola such that |
|
Answer» `hgt3` |
|
| 1732. |
Find dy/dx where y=tan^-1 f(x) |
| Answer» | |
| 1733. |
If (n-m) is odd and |m|ne|n| then int_(0)^(pi)cosmxsinnxdx=.......... |
|
Answer» `(2N)/(n^(2)-m^(2))` |
|
| 1734. |
Find the equation of circles determined by the following conditions. Circle passes through origin and cuts off intercepts a and b from the axes. |
|
Answer» SOLUTION :LET the equation of the circle be `x^2+y^2+2gx+2fy+c=0`  As it passes through the points (a, 0) and (0, 0). As it passes through the points (a, 0) and (0, 0). We have c = 0, `a^2 + 2gs = 0`, `B^2 + 2fb = 0` `therefore` 2g = -a, 2f = -b. `therefore` Equation of the circle is `x^2 + y^2 -ax - by = 0` |
|
| 1735. |
If veca and vecb lie in one plane and vec c and vecd lie on another plane and if the planes are parallel which one of the following is true. |
|
Answer» A)`(veca XX vecb) * (VECC xx VECD)=0` |
|
| 1736. |
There are two bags, one of which contains 3 black and 4 white balls while the other contains 4 black and 3 white balls. A die is thrown. If it shows up 1 or 3, a ball is taken from the 1^(st) bag, but it shows up any other number, a ball is chosen from the 2^(nd) bag. Find the probability of choosing a black ball. |
|
Answer» |
|
| 1737. |
If f(x)=x^(3)+ax^(2)+bx+5sin^(2)x, AA x in R is an increasing function, then ………….. |
|
Answer» `a^(2)-3b-15gt0` |
|
| 1738. |
If bar(a),bar(b) and bar( c ) are three vectors such that bar(a)+bar(b)+bar( c )=bar(0) and |bar(a)|=2,|bar(b)|=3 and |bar( c )|=5, then the value of bar(a).bar(b)+bar(b).bar( c )+bar( c ).bar(a) is ……….. |
|
Answer» 0 |
|
| 1739. |
IF fis differentiablef(x+y)=f(x) f(y)forallx,y, inIRf(3)= 3,f'(0) = 11 ,thenf'(3)= |
| Answer» ANSWER :D | |
| 1740. |
If the normals at P, Q, R of the parabolay^2=4axmeet in O and S be its focus, then prove that.SP . SQ . SR = a . (SO)^2. |
|
Answer» `2^(3)` |
|
| 1741. |
Find the scalar product of the following pairs of vectors and the angle between them. veca = (2,-2,1) and vecb(0,2,4) |
|
Answer» SOLUTION :`veca = (2, -2, 1)` and `VECB = (0,2,4)` Then `veca.vecb = 0-4+4= 0` `IMPLIES veca` is perpendicular to `vecb`. Hence the angle between them is `pi/4` |
|
| 1742. |
If [{:(x,0),(1,y):}]-[{:(2,-4),(-3,-4):}]=[{:(3,5),(6,3):}]-[{:(2,1),(2,1):}] then , x=…., y=….. |
|
Answer» `x=3,y=2` |
|
| 1743. |
If | int_(0)^(pi/2) ( x^2 cos x )/( (1 + sin x) ^(2) ) dx| is equal to (pi = 3.14) |
|
Answer» |
|
| 1744. |
Removesecondterm( secondhigherpowerof x )fromthe equation x^3 -6x^2+10x -3=0 |
|
Answer» |
|
| 1745. |
Find the equation of lines joining the points. (4,-6,1) and (0,3,-1) |
| Answer» Solution :EQUATION of the LINE JOINING the points (4,-6,1) and (0,3,-1) is `(x-4)/(0-4)=(y+6)/(3+6)=(z-1)/(-1-1)` or `(x-4)/4=(y+6)/9=(z-1)/(-2)` | |
| 1746. |
For a two step reaction. AhArrR+B""R+Coverset(k_(2))toP (where, R is a reactive intermediate whose concentration is maintained at some low steady state throughout the reaction). If the concentration of C is very high then the order of reaction for formation of "P" is |
|
Answer» 2 at STEADY STATE `(d[R])/(dt)=0` `(d[R])/(dt)=K_(1)[A]-K_(2)[R][B]-K_(2)[R][C]=0` `K_(1)[A]={K_(2)[B]+K_(2)[C]}[R]` `[R]=(K_(1)[A])/(K_(2){[B]+[C]})` Rate `=K_(2)XX(K_(1))/(K_(2))([A])/([B]+[C])xx[C]` `ul(K_(1)[A])` `=([B])/([C])+1` where C is very high Rate `=K_(1)[A]` `:.` order of reaction` = 1 ""]` |
|
| 1747. |
Resolve (1)/(x^(6)(x+1)) into partial fractions. |
|
Answer» |
|
| 1748. |
Prove that the following functions do not have maxima or minima g (x) = log x |
| Answer» SOLUTION :`G(x)=1/xne0` for any real x `thereforeg(x)` does.t have MAXIMA or minima | |
| 1749. |
Does the number set {0.6,0.5,0.9,0.1} give a probability distribution ? |
| Answer» SOLUTION :As `0.6+0.5+0.9+0.1=2.1lt1`, the GIVEN SET is not a PROBABILITY DISTRIBUTION. | |
| 1750. |
A copany manufactures two types of toys, A and B. Type A requires 5 minutes each for cutting and 10 minutes each for assembling. Type B requires 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours available for cutting and 4 hours available for assembling in a day. The profit is Rs.50 each on type A and Rs.60 each on type B. How many toys of each type should the company manufacture in a day to maximize the profit? |
|
Answer» Maximize `Z=50x+60y.` |
|