InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 2251. |
A(2,3) and B(-7, -12) are conjuigate point w.r.tS= x^(2) + y^(2) - 6x - 8y - 1 = v,. The angle between the circle S = 0 and the circle having AB as diameter is |
|
Answer» `(PI)/(3)` |
|
| 2252. |
A : ABCD is a parallelogram. If G is the point of intersection of its diagonals and 'O' is any point then OA + OB + OC + OD = 4OG R : In a parallelogram diagonals bisect each other. |
|
Answer» A, R are CORRECT, R is correct EXPLANATION of A |
|
| 2253. |
If points A (bara), B (barb) and C (barc) are such that 2bara + 3barb - bar5c = bar0, then their relative positions are |
| Answer» Answer :C | |
| 2254. |
If ane0,bne0,cne0 and |{:(0,x^2+a,x^4+b),(x^2-a,0,x-c),(x^3-b,x^2+c,0):}|=?, for x=0 |
|
Answer» 1 |
|
| 2255. |
The set z = { 1, 2, 3, 4} is an abelian group under |
|
Answer» ADDITION MODULO 4 |
|
| 2256. |
The locus of the point z = x +iy satisfying the equation |(z-1)/(z+1)|=1 is given n=by |
|
Answer» ` X= 0` |
|
| 2257. |
Let alpha , beta and gamma be the roots of the equation x^3 - x - 1 = 0 . If P_k = (alpha)^k + (beta)^k + (gamma)^k , k gt= 1 , then which one of the following statements is not true? |
|
Answer» `P_3 = P_1+P_2 + 1` |
|
| 2258. |
Select the Correct Option The value of int(dx)/(1-9x^2) is |
|
Answer» 1/6log|(1+3x)/(1-3x)|+C |
|
| 2259. |
int dx/((x-1) sqrt(2x +3) |
| Answer» | |
| 2260. |
int dx/((x-3)sqrt x |
| Answer» | |
| 2261. |
int sqrtx/(x+2)dx |
| Answer» | |
| 2262. |
Reflex which protect the alveoli from over inflation is :- |
|
Answer» WITHDRAWL reflex |
|
| 2263. |
Number of solutions of the equation sinx-sin2x+sin3x=2cos^(2)x-2cosx is (0,pi) is |
|
Answer» 1 |
|
| 2264. |
Find the area of region enclosed by curves y=sin pix, y=x^(2)-x, x=2 |
|
Answer» |
|
| 2265. |
Find the area of the region bounded by Find the area enclosed between the curve y=x^(2)+2, x-axis, x = 1 and x = 2 |
|
Answer» |
|
| 2266. |
Find a unit vector in the direction of vec(PQ), where P and Q have coordinates (5, 0, 8) and (3, 3, 2), respectively. |
|
Answer» |
|
| 2267. |
If f(a + b - x) = fx, then int_a^b x f(x) dx is equal to : |
|
Answer» `(a+B)/2int_(a)^(b)F(b-X)DX` |
|
| 2268. |
The roots of the equation x^(3) - 14x^(2) + 56x- 64= 0are in …… progression |
|
Answer» `A.G.P` |
|
| 2269. |
Integrate the following functions (i) inte^(sin^(2)x)(cosx+cos^(3)x) (ii) int(7sinx+cosx)/(4si nx-3cosx)dx (iii) introot(3)((sin^(n)x)/(cos^(n+6)x))dx (iv) int((4x+6)/(x^(2)+3x+100))dx |
|
Answer» `x+ln|(4sinx-3cosx)|+c` `(TAN^(N/3+3)x)/((n)/(3)+1)+c` `2ln|x^(2)+3x+100|+c` |
|
| 2270. |
If x=1 +log_(e) bc, .......... |
|
Answer» Similarly `y=log_(B) abc` `z=log_(c) abc` `(XYZ)/(xy+yz+zx)=1/(1/x+1/y+1/z)=1/(log_(abc) abc)=1` |
|
| 2271. |
Find all the points of local maxima and local minima of the function f given by f(x)=2x^(3)-6x^(2)+6x+5. |
|
Answer» |
|
| 2272. |
If log_(e )4=1.3868, then approximate value of log_(e )4.01= ………….. |
|
Answer» `1.3867` |
|
| 2273. |
int (2x+2)/(sqrt(x^2-4x-5))dx= |
|
Answer» `SQRT(x^2-4x-5)+log|x+sqrt(x^2-4x-5)|C` |
|
| 2274. |
Integrate the following : int(x^2+sqrtx)^2dx |
|
Answer» SOLUTION :`INT(x^2+sqrtx)^2dx` =`int(x^4+x+2x^2xxsqrtx)DX` =`intx^4dx`+`intxdx`+`2intx^(1/2)dx` `1/5x^5+1/2x^2+2xx2/7x^(7/2)+C` `1/5x^5+1/2x^2+4/7x^(7/2)+C` |
|
| 2275. |
If a, b and c are three distinct real numbers, and((x - b) (x - c))/( (a - b) (a - c)) + ((x - c)(x - a))/((b - c) (b - a)) + ((x - a) (x - b))/((c - a)(c - b))=Ax^(2) + Bx + C then (A - 2 B + 4 C)/( 2 A - B + C) is equal to _______ |
|
Answer» |
|
| 2276. |
The symmetric part of the matrix A = ((1,2,4),(6,8,2),(2,-2,7)) is |
|
Answer» `((0, -2, -1),(-2,0,-2),(-1,-2,2))` |
|
| 2277. |
The pair of lines whose direction cosines are given by : 3l+m+5n=0,6mn-mn-2nl+5l=0are : |
|
Answer» PARALLEL |
|
| 2278. |
If the angle made by a straight line with the coordinate axes are alpha , pi/2 - alpha , betathen betais equal to |
| Answer» ANSWER :C | |
| 2279. |
The function f(x)=(1-cos ax)/(1-cos bx)"for "x ne 0, f(0)=a/b" at x= 0 is " |
|
Answer» only I is true |
|
| 2281. |
In a bank, principal increases continuously at the rate of5% per year.In how many years Rs 1000 double itself? |
|
Answer» |
|
| 2282. |
int_0^(pi/2)cos^9thetad theta |
| Answer» SOLUTION :`int_0^(pi/2)cos^9thetad theta=8/9 CDOT 6/7 cdot 4/5 cdot 2/3=(384)/405` | |
| 2283. |
If bar = hat i + hat j and bar b = 2 hat i - hat kthen the intersection piont of the linesbar r xx bar a = bar b xx bar aand bar r xx bar b = bar a xx bar b is ............. |
|
Answer» `hat i + hat j - hat k` |
|
| 2284. |
The values ofoverset(10)underset(r=1)Sigma r P (r,r) i |
|
Answer» <P>P(11,11) |
|
| 2285. |
If alpha is a non real root of x^6=1 then (alpha^5+alpha^3+alpha+1)/(alpha^2+1)= |
|
Answer» `ALPHA^2` |
|
| 2286. |
Plot the region of the points P(x,y) satisfying 2 gtmax. {|x|, |y|}. |
|
Answer» Solution :We have `2 gt` MAX.`{|x|, |y|}` `therefore 2 gt |x| and 2 gt |y|` `i.e., -2 LT x lt 2 " and" -2 lt y LT2.` Thus, common region of these inequalities is the square FORMED by lines `x = +-2 " and " y= +-2.` 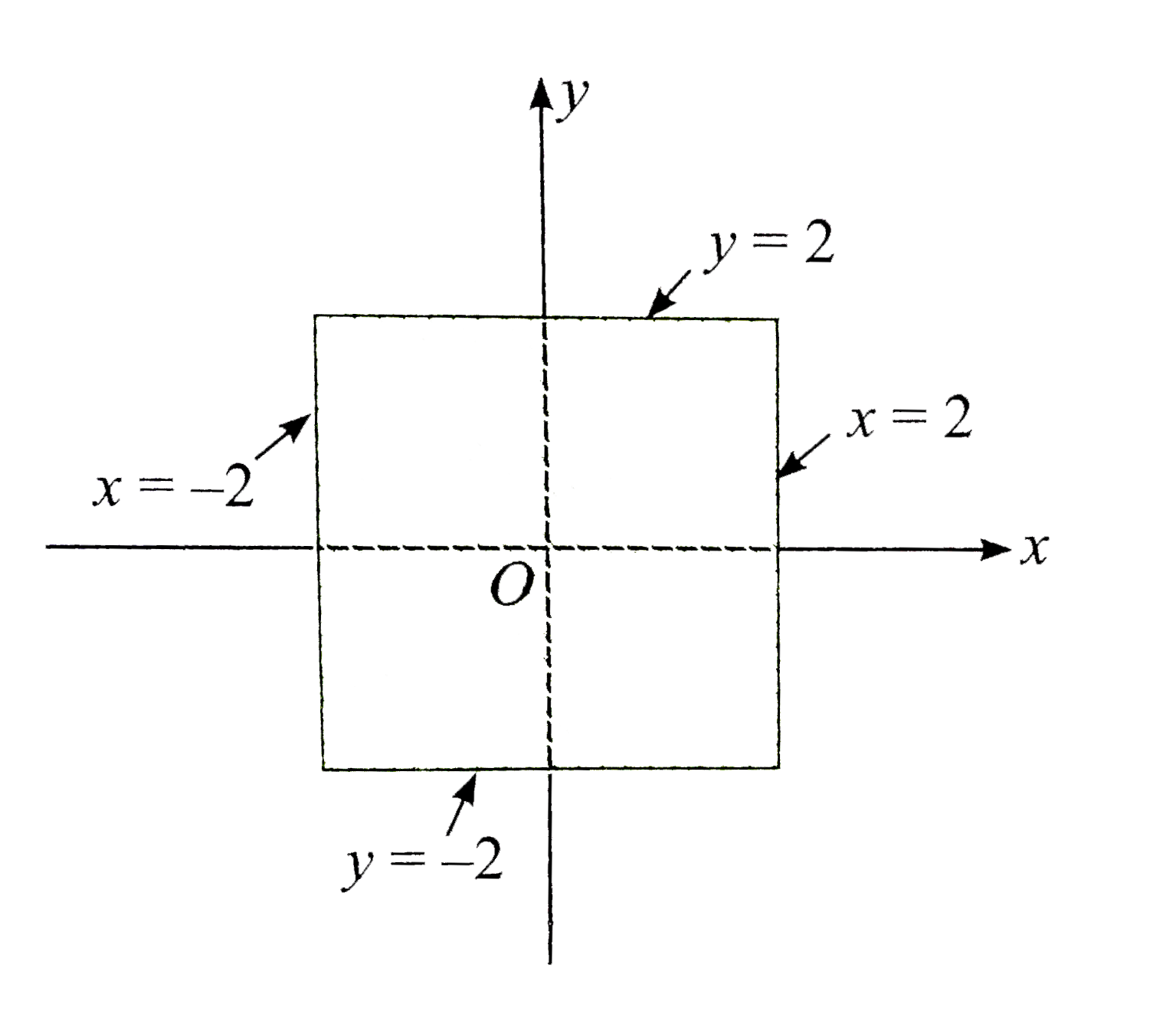
|
|
| 2287. |
Let f: {1,3,4} rarr {1,2,5} and g : {1,2,5} rarr {1,3} be given by f={(1,2),(3,5),(4,1) and g {(1,3),(2,3) , (5,1) } . Write down gof. |
|
Answer» |
|
| 2288. |
The subnormal at any point of a curve is of constant length '8'. Then the differential equation of the family of curve is |
|
Answer» `(dy)/(DX) = 8y` |
|
| 2289. |
If l_1, m_1, n_1, and l_2, m_2, n_2 are the direction cosines of two mutually perpendicular lines, show that the direction cosines of the line perpendicular to both of these arem_1n_2-m_2n_1,n_1l_2-n_2l_1,l_1m_2-l_2m_1 |
|
Answer» `m_1n_2-m_2n_1,n_1l_2-n_2l_1,l_1m_2-l_2m_1` |
|
| 2290. |
If tangent is drawn at (x_(1), y_(1)) on the hyperbola (x^(2))/4-(y^(2))/3=1 intersect the x axis at C(alpha, 0) and y axis at D(0,beta) then int_(2)^(4sqrt(2)) (alpha)/(beta) dx_(1) is |
|
Answer» `(3pi)/8` `:. int_(2)^(4sqrt(2))(4//x_(1))/(-4//sqrt(x_(1)^(2)-4)) dx_(1)=- int_(2)^(4sqrt(2)) (dx_(1))/(x_(1)sqrt(x_(1)^(2)-4))` (Put `x_(1)=2sec theta, dx_(1)=2sec theta tan theta d theta`) `=-int_(0)^(2)((pi)/4 2sec theta tan theta d theta)/(2 sec theta.2tan theta)=-(pi)/8` |
|
| 2291. |
A wire suspended vertically from one of its ends is stretched by attaching a weight of 200 N to the lower end. The weight stretches the wire by mm. Then the elastic energy stored in the wire :- |
|
Answer» 0.1 J |
|
| 2292. |
Statement I In a Delta ABC, if cos ^(2)""A/2 + cos ^(2)""B/2 +cos ^(2) ""C/2=y(x^(2)+(1)/(x^(2))) then the maximum value of y is 9/8. Statement II In a Delta ABC, sin ""A/2 . Sin ""B/2 sin ""C/2 le 1/8 |
|
Answer» Both STATEMENT I and Statement II are correct and Statement II is the correct explanation of Statement I |
|
| 2293. |
For each of the differential equations given in Exercises 13 to 15, find a particular solution satisfying the given condition: 13. (dy)/(dx) + 2 y tan x = sin x, y = 0 when x = (pi)/(3) |
|
Answer» |
|
| 2295. |
ABC is a triangle such that angleABC=2angleBAC. If AB is fixed and locus of C is a hyperbola, then the eccentricity of the hyperbola is |
|
Answer» |
|
| 2296. |
The sum of the coefficients of even powers of x in the expansion of(1+x+x^2+x^3)^5 is |
|
Answer» 510 |
|
| 2297. |
(Diet problem): A dietician wishes to mix two types of foods in such a way that vitamin contents of the mixture contain atleast 8 units of vitamin A and 10 units of vitamin C. Food 'I' contains 2 units/kg. of vitamin A and 1 unit/kg. of vitamin C. Food 'II' contains 1 unit/kg. of vitamin A and 2 units/kg of vitamin C. It costs Rs. 50 per kg. to purchase Food 'I' and Rs. 70 per kg. to purchase Food 'II'. Formulate this problem as a linear programming problem to minimise the cost of such a mixture. |
|
Answer» |
|
| 2298. |
Show that the function f: R rarr { x in R: -1 lt x lt 1 }defined by f(x)=(x)/(1+|x|), x in Risone- one and onto function . |
|
Answer» Solution : Let x, `y in R` and, f(x)=f(y) `rArrx/(1+|x|)=y/(1+|y|)` If x is positve and y is negative then `x gt y ` `rArrx-y gt 0 and 2xy LT 0 ` `thereforex/(1+x)=y/(1-y)` `rArry+ XY =x -xy` `rArr2xy = x-y` which is impossible then `f(x)=f(y)rArr (x)/(1+x)=(y)/(1+y)` `rArrx+y` If x and y both are negative then `f(x)=f(y)rArrx/(1-x)=y/(1-y)` `rArrx-xy = y-xy` `rArrx=y` Therefore , FIS one - one Let y `in ` R be such that `-1 lt y lt 1` If y is negative then `x=y/(1+y) in R` is such that `f(x)=f((y)/(1+y))=((y)/(1+y))/(1+|(y)/(1+y)|)=((y)/(1+y))/(1-y/(1+y))=y` IFY is positive then `x=y/(1-y) in R` is such that `f(x)=f(y/(1-y))=((y)/(1-y))/(1+((y)/(1-y)))=((y)/(1-y))/(1-y/(1+y))=y` `therefore` f is ONTO Therefore f is one - one onto . |
|
| 2299. |
A sphere with volumn 36pi cubic inches is inscribed in a cube so that the sphere touches the cube at 6 points. What is the surface area, in square inches, of the cube ? |
|
Answer» |
|
| 2300. |
If d = x (a xx b) + y (b xx c) + z (c xx a) and [a b c] = 1/8, then x + y + z = |
| Answer» Answer :A | |