InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 2151. |
Find the equation of the circle with centre C and radius r where C = (a,-b) , r= a+b |
|
Answer» |
|
| 2152. |
Definite integration as the limit of a sum : lim_(ntooo)(1)/(n)sum_(r=n+1)^(2n)log(1+(r)/(n))=............. |
|
Answer» `log((27)/(4E))` |
|
| 2154. |
The radius of the circle which has the lines x+y-1=0, x+y-9=0 as tangents is |
|
Answer» `SQRT(2)` |
|
| 2155. |
Let I_(n)=int_(0)^(pi//4) tan^(n)x dx. Statement-1: (1)/(n+1)lt 2I_(n) lt (1)/(n-1) for all n=2,3,4,….. Statement-2: I_(n)+I_(n-2)=(1)/(n-1),n=3,4,5,…... |
|
Answer» Statement-1 is true, Statement-2 is True,Statement-2 is a correct explanation for Statement-1. `I_(n)+I_(n-2)=UNDERSET(0)overset(PI//4)int tan^(n)x dx+underset(0)overset(pi//4)int tan^(n-2)x dx` `rArr I_(n)-I_(n-2)=underset(0)overset(pi//4)int tan^(n-2)x sec^(2)x dx=[(tan^(n-1)x)/(n-1)]_(0)^(pi//4)=(1)/(n-1)` So, statement-2 is true. We know that `0 lt tan xlt1` for ll `x in (0,(pi)/(4))` `rArr tan^(n+2)xlt tan^(n-2)x` for all `x in (0,(pi)/(4))` `rArr underset(0)overset(pi//4)int tan^(n+2)x dx lt underset(0)overset(pi//4)int tan^(n-2)x dx` `rArr I_(n+2)lt I_(n)lt I_(n-2)` `rArr I_(n)+I_(n+2)lt 2I_(n)+I_(n-2)` `rArr (1)/(n+1)ltI_(n)lt(1)/(n-1)""`[Using statement-2] So, statement-1 is true and statement-2 is a correct explanation for statement-1. |
|
| 2156. |
For a normal distribution if the mean is M, mode is M_(0) and median is M_(d), then |
|
Answer» `M GT M_(d) gt M_(0)` |
|
| 2157. |
Show that the relation R in the set {1,2,3} given by R = {(1,2),(2,1)} is symmetric but neither reflexive nor transitive. |
|
Answer» |
|
| 2158. |
(cos 13^(@) - sin 13^(@))/(cos 13^(@) + sin 13^(@)) + (1)/(cot 148^(@)) is equal to |
| Answer» ANSWER :c | |
| 2159. |
If the equation (x + m)^(2) - (x + n)^(2) = ( m - n)^(2) where m , n are non- zero constants and m^(2) ne n^(2) , satisfied by x = pm + pn , then the ordered pair (p , q) is equal to |
| Answer» ANSWER :A | |
| 2160. |
The sum of two numbers is 13, and their product is 30. What is the sum of the squares of the two numbers? |
| Answer» ANSWER :D | |
| 2161. |
State with reason,"Collection of all residents of Odisha who will live for more than 100 years " is set or not ? |
| Answer» Solution :It is not t set, as we do not KNOW, that who will LIVE for more than 100 YEARS. | |
| 2162. |
Integrate the following functions : int(2x+5)/(x^(2)+5x+9)dx |
|
Answer» |
|
| 2163. |
Let A=[(0,2),(0,3)] and B=[(2,3),(0,0)], then AB equals : |
|
Answer» `[(0,6),(0,0)]` |
|
| 2164. |
If the coefficient of x^(3) is 1140 in the expansion of (1+2x+kx^(2)), then the value of k is______. |
|
Answer» |
|
| 2165. |
Find the order and degree (if defined) of the following differential equations. y' + 5y = 0 |
| Answer» Solution :The HIGHEST ORDER DERIVATIVE in the differential equation is y. . Order of the differential equation = !, The degree of y. is 1. `therefore` The degree of the differential equation = 1. | |
| 2166. |
Find the angles between the pair of lines whose slopes are , sqrt3,-1 . |
|
Answer» SOLUTION :LET `m_1=sqrt3,m_2=-1` `THEREFORE` `TANTHETA=(m_2-m_1)/(1+m_1m_2)=(-1-sqrt3)/(1-sqrt3)` =`((sqrt3+1)/(1+sqrt3))=(sqrt3+1)/(sqrt3-1)=tan75^@ ` `therefore` `theta=75^@`. |
|
| 2168. |
If sum_(i=1)^(4)a_(i)^(2)x^(2)-2sum_(i=1)^(4)a_(i)a_(i+1)x+sum_(i=1)^(4)a_(i)^(2)+1) le 0, " where " a_(i) gt 0 and all are distinct. Then, |
|
Answer» `a_(1)+a_(5) GT 2a_(3)` |
|
| 2169. |
The point P(alpha,alpha +1) will lie inside the triangle whose vertices are A(0,3), B(-2,0) and C(6,1) if |
|
Answer» `alpha =- 1` Equation of AC is `X +3y - 9 =0` Equation of BC is `x - 8y +2 = 0` 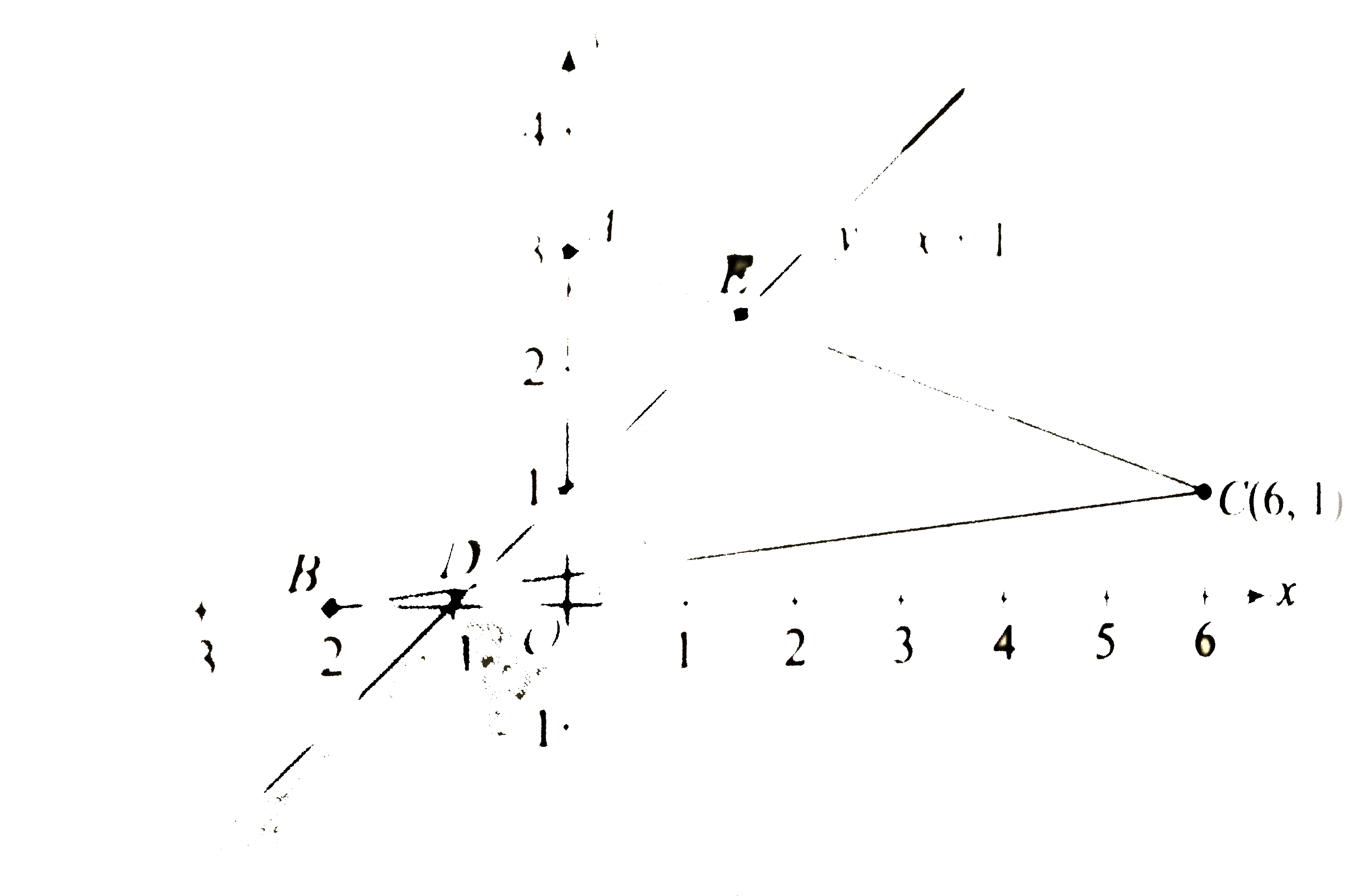 `P (alpha, alpha +1)` lies on the line `y = x +1` whichcuts BC at `D(-(6)/(7),(1)/(7))` and AC at `E ((3)/(2),(5)/(2))` `:. alpha` must lie between `-(6)/(7)`and `(3)/(2)`. |
|
| 2170. |
Find the vector equation of the line passing through (1, 2, 3) and parallel to the planes vecr.(hati-hatj+2hatk)=5 and vecr.(3hati+hatj+hatk)=6 |
|
Answer» |
|
| 2171. |
Find the unit vector in the direction of the vector 2hati-2hatj+hatk. |
|
Answer» |
|
| 2172. |
If sum_(i=1)^(15)x_(i)=45,A=sum_(i=1)^(15)(x_(i)-2)^(2) B=sum_(i=1)^(15)(x_(i)-3)^(2) and C=sum_(i=1)^(15)(x_(i)-5)^(2) then Statement 1: min(A,B,C)=A Statement 2: The sum of squares of deviations is least when taken from man. |
|
Answer» Statement 1: is TRUE, Statement 2 is True , Statement 2 ISA correct explanation for statement 1 `implies "min" (A,B,C)=B` |
|
| 2174. |
A slip of paper is given to a person A who marks it either with a plus sign or a minus sign. The probability of his writing a plus sign is 1//3. A passes the slip to B, who may either leave it alone or change the sign before passing it to C. Next C passes the slip to D after perhaps changing the sign. Finally D passes it to a refere after perhaps changing the sign. B,C,D each change the sign with probability 2//3. The probability that the referee observes a plus sign on the slip if it is known that A wrote a plus sign is |
|
Answer» `14//27` `E_(1)=` Event that `B` wrote a plus sign `E=` Event that the REFEREE observes a plus sign. Given `P(E_(1))=(1)/(3)impliesP(E_(2))=(2)/(3)` `P(E//E_(1))=` PROBABILITY that none of `B`, `C`, `D` change sign `+` Probability that exactly two of `B,C,D` change sign `=(1)/(27)+3((1)/(3)xx(2)/(3)xx(2)/(3))=(13)/(27)` `P(E//E_(2))=` Probability that all of `B,c,d` change sign `+` Probability that exactly one of `B,C,D` changes sign ,brgt `=(8)/(27)+3((2)/(3)xx(1)/(3)xx(1)/(3))=(14)/(27)` `:.P(E_(1)//E)=(13)/(41)` (Using Bayes' Theorem) |
|
| 2175. |
A slip of paper is given to a person A who marks it either with a plus sign or a minus sign. The probability of his writing a plus sign is 1//3. A passes the slip to B, who may either leave it alone or change the sign before passing it to C. Next C passes the slip to D after perhaps changing the sign. Finally D passes it to a refere after perhaps changing the sign. B,C,D each change the sign with probability 2//3. If the refree observes a plus sign on the slip then the probability that A originally wrote a plus sign is |
|
Answer» `13//41` `E_(1)=` Event that `B` wrote a plus sign `E=` Event that the referee observes a plus sign. Given `P(E_(1))=(1)/(3)impliesP(E_(2))=(2)/(3)` `P(E//E_(1))=` Probability that none of `B`, `C`, `D` change sign `+` Probability that exactly two of `B,C,D` change sign `=(1)/(27)+3((1)/(3)XX(2)/(3)xx(2)/(3))=(13)/(27)` `P(E//E_(2))=` Probability that all of `B,c,d` change sign `+` Probability that exactly one of `B,C,D` changes sign ,brgt `=(8)/(27)+3((2)/(3)xx(1)/(3)xx(1)/(3))=(14)/(27)` `:.P(E_(1)//E)=(13)/(41)` (USING BAYES' Theorem) |
|
| 2176. |
Match the following. {:( "I." C_0 + 3.C_1 + 5. C_2 + …...(2n + 1). C_n=,"a)" (n+1)2^(n)),( "II." 3. C_0+7. C_1 + 11. C_2 + ….+ (4n+3). C_n=,"b)" (2n+3)2^(n)),( "III." C_0 + 4. C_1 + 7. C_2 + …. (n+1) "terms" =, "c)" (2n+3) 2^(n-1)),( "IV." (3n+2)^(n) C_0 + (3n - 1) ^n C_1+ (3n-4)^n C_2 + .......+ (""^n C_n)=,"d)" (3n+4) 2^(n-1)):} |
|
Answer» a, b, C, d |
|
| 2177. |
Let abs(a)=sqrt(3), abs(b)=5, b*c=10, angle between b and c is equal to pi//3. If a is perpendicular to b times c, " then "abs(a times (b times c))=_________ |
|
Answer» |
|
| 2178. |
Let A, B, C be three events and barA, barB, barC be their corresponding complementary event. If the probabilities of events B, AnnBnnbarC and barA nnB nnbarC are (5)/(6),(1)/(2) and (1)/(4) respectively, then the probability of the event BnnC is |
|
Answer» `(1)/(12)` |
|
| 2179. |
What is the correct order of nitration of the following compounds? {:(C_(6)H_(5)CH_(3),C_(6)H_(6),C_(6)D_(6),C_(6)T_(6),C_(6)H_(5)Br,C_(6)H_(5)overset(+)NR_(3),C_(6)H_(5)NMe_(2)),("a","b"," c"," d","e","f","g"):} |
|
Answer» `G GT a gt b gt c gt d gt e gt F` `:. C_(6)H_(6)=C_(6)D_(6)=C_(6)T_(6)` |
|
| 2180. |
lim_(xto0) {(1)/(x3sqrt(8+x)-(1)/(2x))} is equal to |
|
Answer» `(1)/(12)` |
|
| 2181. |
Amar and Bimal are two contestants for an election, probability that Amar will win is 1/4 and that Bimal will win the election is 1/5, then what is probability that either Amar or Bimal will win the election. |
|
Answer» `13//20` |
|
| 2182. |
Find the number of ways of forming a committee of 5 members out of 6 Indians and 5 Americans so that always the Indians will be in majority in the committee. |
|
Answer» |
|
| 2183. |
The volume of the parallelepiped whose coterminous edges are represented by the vectors 8vec(b)xxvec(c),3vec(c)xxvec(a)and4vec(a)xxvec(b), where vec(a)=(1+sintheta)hat(i)+costhetahat(j)+sin2thetahat(k), vec(b)=sin(theta+(2pi)/(3))hat(i)+cos(theta+(2pi)/(3))hat(j)+sin(2theta+(4pi)/(3))hat(k), vec(c)=sin(theta-(2pi)/(3))hat(i)+cos(theta-(2pi)/(3))hat(j)+sin(2theta-(4pi)/(3))hat(k) is 18 cubic units, then the values of theta, in the interval (0,(pi)/(2))," is/are" |
|
Answer» `(pi)/(9)` |
|
| 2184. |
If A+B+C+D= 2pi , " then " -4 cos""((A+B)/(2)) sin""((A+C)/(2)) cos""((A-D)/(2))= |
|
Answer» `SIN A + sin B+ sin C-sin D ` |
|
| 2185. |
int(Inx)/x^5dx |
|
Answer» Solution :`int(INX)/x^5dx=int1nx.x^-5dx` [TAKE 1n x as FIRST and `x^-5` as second function] =`1nx.x^-4/-4-int1/x.x^-4/-4dx` =`-(1n x)/(4x^4) +1/4intx^-5dx` =`-(1nx)/(4x^4)+1/4 x^-4/-4+C` =`-(1nx)/(4x^4)-1/(16x^4)+C` |
|
| 2186. |
Correct order of indicated bond length is/are: |
|
Answer» `CH_(2)OVERSET(a)=CH-O"Me" lt O_(2)N-CH_(2)overset(b)=CH-O"Me"` |
|
| 2187. |
If a^(2)-3(b-|d|) lt 0 prove that f(x) = x^(3) + ax^(2) + bx +dsinx is an increasing function in the set of real number R. |
| Answer» | |
| 2188. |
If A, B and C are three sets such that A nn B=A nn C and AuuB=AuuC, then |
| Answer» Answer :B | |
| 2189. |
If int(2x^(2)+5)/(x^(2)+a)dx=f(x), where f(x) is a polynomial or ratio of polynomials, then the number of possible value(s) of a isequal to |
|
Answer» 0 |
|
| 2190. |
Find the value of k if the following equations have equal roots i) x^(2)–2(1+3k)x+7(3+2k)= 0 ii) x^(2) -15 - k(2x – 8) = 0 iii) (3k+1)x^(2)+2(k+1)x+k=0 iv) x^(2)+2(k+2)x+9k=0 |
|
Answer» |
|
| 2191. |
Let P(n) be a statement such that truth of P(n)impliesthe truth of P(n + 1)[ n inN, then P(n) is true |
|
Answer» `AA N GT 1` |
|
| 2192. |
Computethe shortestdistancebetweenthe lines vec(r )=(hat(i) -hat(j)) + lambda (2hat(i) -hat(k))" and" vec(r ) =(2hat(i) -hat(j))+ mu (hat(i) - hat(j) -hat(k)) Determinewhether theselinesintersect of not. |
|
Answer» |
|
| 2193. |
Assertion (A) : The remainder of x^(3)+2x^(2)-5x-3 which is divided by x-2 is 3. Reason (R) : The remainder of the polynomial f(x) when divided by x-a is f(a) |
|
Answer» Both A & R are TRUE and R is CORRECT EXPLANATION of A |
|
| 2194. |
Fundamental theorem of definite integral : int_(a)^(b)(logx)/(x)dx=...... (where a binR^(+) ) |
|
Answer» `(1)/(2)LOGAB` |
|
| 2195. |
Determine the truth of falsity of the{1,2} in {1,2,3} propositions with reasons. |
| Answer» SOLUTION :`{1,2} in {1,2,3}` is FALSE, as {1,2} is not an ELEMENT of {1,2,3} but it is a SUBSET. | |
| 2196. |
In a bivariate distribution the regression equation of y on x is 8x – 10y + 66 = 0. If barx= 13, find bary |
|
Answer» |
|
| 2197. |
Show that a function p is a polynomial function is continuous. |
|
Answer» <P> |
|
| 2198. |
Line L has intercepts a and b on the axes of co ordinates. When the axes are rotatedthrough a givenn angle, keeping the origin fixed, the straight line L has intercpets p and q on the transformed axes. Prove that1/(a^(2))+1/(b^(2))=1/(p^(2))+1/(q^(2)). |
|
Answer» |
|
| 2199. |
Contraction of muscles results from :- |
|
Answer» A contraction of MYOSIN filaments. |
|
| 2200. |
If three dice are thrown, the probability that they show the numbers in A.P.is |
|
Answer» `(1)/(36)` |
|