Explore topic-wise InterviewSolutions in .

This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.

2201.

A line in 3-dimensional space makes an angle theta(0ltthetalepi//2) with both x and y-axis. Then the set of all values of theta is the interval:

Answer»

`(0,(pi)/(4)]`
`[(pi)/(6),(pi)/(3)]`
`[(pi)/(4),(pi)/(3)]`
`((pi)/(6),(pi)/(2)]`

Answer :C
Discussion
2202.

Solve graphically x + y ge 1

Answer»

SOLUTION :
Discussion
2203.

If (2,0),(0,1),(4,5)and (0,c) are concy- clic, and then find c.

Answer»


ANSWER :`c=1 or 14/3`
Discussion
2204.

A particle which is moving along x-axis has acceleration at any time t like a(t)=(12t^2-30t)m//s^2.At t=0, velocity of particle is 7 m/s and at t=1 sec, particle is at x=6m. Choose the CORRECT function for position at any time t.

Answer»

`x=t^4-5t^3+7t+3`
`x=2t^4-5t^3+7t+3`
`x=t^4-3t^3+7t+3`
`x=2t^4-5t^3+5t+3`
Discussion
2205.

Indicate the relation which is true:

Answer»

`TAN|tan^(-1)x|=|x|`
`cot|cot^(-1)x|=|x|`
`tan^(-1)|tanx|=|x|`
`sin|sin^(-1)x|=|x|`

ANSWER :A::B::D
Discussion
2206.

Evalute the following integrals int x^(2) " sin "x^(3)dx

Answer»


ANSWER :`2 [ e^(4//2) + 1 - LOG (e^(1//2) + 1) ] + C `
Discussion
2207.

-N = O group can show

Answer»

`+M` EFFECT
`-M` effect
`-I` effect
All of these

Answer :D
Discussion
2208.

Using elementry transformation, find the inverse of the matrices. A = [(7,-10),(-2,3)]

Answer»

SOLUTION :`A^(-1) = [(7,-10),(-2,3)]`
Discussion
2209.

Two mutually exclusive events having nonzero probabilities of occurrence cannot be ________?

Answer»

<P>

ANSWER :` P(A)= (4)/(13)`
Discussion
2210.

underset(x to 0)"Lt" (tan^(3)x-sin^(3)x)/(x^(5))=

Answer»

`5/2`
`3/2`
`3/5`
`2/5`

ANSWER :B
Discussion
2211.

Let veca = 2hati+hatj, vecb = -hati+3hatj+hatk and vecc = hati+2hatj+5hatk be three vectors. Find vecaxx(-vecb)

Answer»

SOLUTION :
Discussion
2212.

State with reason, "All finite subsets of the set Z of integers " is set or not ?

Answer»

SOLUTION :It is a SET, as it is WELL DEFINED.
Discussion
2213.

Write thevectorequationsof each ofthe followinglinesand hencedeterminethe distance betweenthem: (x-1)/(2)=(y-2)/(3)=(z+4)/(6)" and" (x-3)/(4) =(y-3)/(6)=(z+5)/(12)

Answer»


Solution :Thegiven lines are`L_(1) : vec( r) =(hat(i) +2HAT(j)-4hat(K)) + lambda (2hat(i) +3hat(j) +6hat(k))`
`L_(2) : vec(r ) =(3hat(i) + 3hat(j) -5hat(k))+ 2mu (2hat(i) +3hat(j) +6hat(k))`
Now FIND thedistancebetweenthe PARALLELLINES `L_(1)" and" L_(2)`
Discussion
2214.

If every pair from among the equations x^(2)+px +qr=0, x^(2)+qx +rp=0 and x^(2)+rx +pq=0 has a common root, then the sum of the three common roots is

Answer»

`2(p+q+r)`
`p+q+r`
`-(p+q+r)`
PQR

ANSWER :B
Discussion
2215.

A clrcle whose centre lies on the hyperbola (x ^(2))/(a ^(2)) + (y ^(2))/(b ^(2)) =1intersects the rectangular hyperboal xy = c ^(2) in four points. Show that the locus of the centre of the locus of the centroid of triangle formed by any three points of intersectivon is (x ^(2))/(a^(2)) - (y ^(2))/(b ^(2)) = ((2)/(3)) ^(2).

Answer»


Answer :the hyperbola `(X ^(2))/(a ^(2)) - (y ^(2))/(B ^(2)) = ((2)/(3)) ^(2)`
Discussion
2216.

If A,B are two events such that P(A)=0.3, P(B)=0.4,P(AcupB)=0.6 Find P(B | A)

Answer»

<P>

SOLUTION :`P(B/A)=(P(ACAPB))/(P(A))=0.1/0.3=1/3`
Discussion
2217.

The real number k for which the equation, 2x^(3) + 3x + k = 0 has two distinct real roots in [0,1]

Answer»

LIES between -1 and 0
does not EXIST
lies between 1 and 2
lies between 2 and 3

ANSWER :2
Discussion
2218.

Find the second order derivatives of the function e^(x) sin 5x.

Answer»


Answer :`2E^(X) (5 COS 5x-12 sin 5x)`
Discussion
2219.

The relation R={(1,1),(2,2),(3,3)} on the set {1, 2, 3) is

Answer»

SYMMETRIC only
REFLEXIVE only
transitive only
an EQUIVALENCE RELATION

ANSWER :D
Discussion
2220.

Find the number of ways of arranging the letters of the word. PERMUTATION

Answer»


ANSWER :`(11!)/(2!)`
Discussion
2221.

3x+4y-7=0 is normal to 4x^(2)-3y^(2)=1 at the point

Answer»

(-3,4)
(1,1)
(2,1/4)
(5,-2)

ANSWER :B
Discussion
2222.

If the line (x-1)/(2)=(y-1)/(3)=(z+2)/(2) lies in the plane x+By-3z+D=0, then the values of B and D are

Answer»

`(4)/(3),(-25)/(3)`
`(-4)/(3),(-25)/(3)`
`(3)/(4),(25)/(4)`
`(-3)/(4),(-25)/(4)`

ANSWER :A
Discussion
2223.

Evaluate the following integrals. int(x+2)sqrt(x+1)dx

Answer»


ANSWER :`(2)/(15)(3x+8)(x+1)^(3//2)+C`
Discussion
2224.

If the roots of ax^(2)+ax+c=0are in the ratio p : q, then sqrt((p)/(q)) +sqrt((q)/(p))=0

Answer»

`SQRT((a^(2))/(c ))`
`sqrt((a)/(2c))`
`sqrt((a)/(c ))`
NONE of these

Answer :c
Discussion
2225.

What is the smallest positive integer t such that threre exist integer n_1,n_2 .....n_1 with (n_1^3+n_2^3+......+n_1^3=4000^(4000))

Answer»


ANSWER :4
Discussion
2226.

3x^(2) - 5x+2 5x^(2) - 2x -6 Which of the following is the sum of the two polynomials shown above?

Answer»

`8X^(2) -7X -4`
`8x^(2) + 7x -4`
`8x^(4) - 7x^(2) -4`
`8x^(4) + 7x^(2) -4`

ANSWER :A
Discussion
2227.

A cottage industry manufactures pedestal lamps and wooden shades, each requiring the use of a grinding/ cutting machine and a sprayer. It takes 2 hours on grinding/cutting machine and 3 hours on the sprayer to manufacture a pedestal lam. It takes 1 hour on the grinding/cutting machine and 2 hours on the sprayer to manufacture a shade. On any day, the sprayer is available for at the most 20 hour and the grinding/ cutting machine for at the most 12 hours. The profit from the sale of a lamp is Rs. 5 and that from a shade isRs. 3. Assuming that the manufacturer can sell all the lamps and shadesthat the produces how should be scehdule his daily production in order to maximise his profit?

Answer»

Solution :Let the MANUFACTURE makes `x` pedestal lamps and `y` wooden shades per day then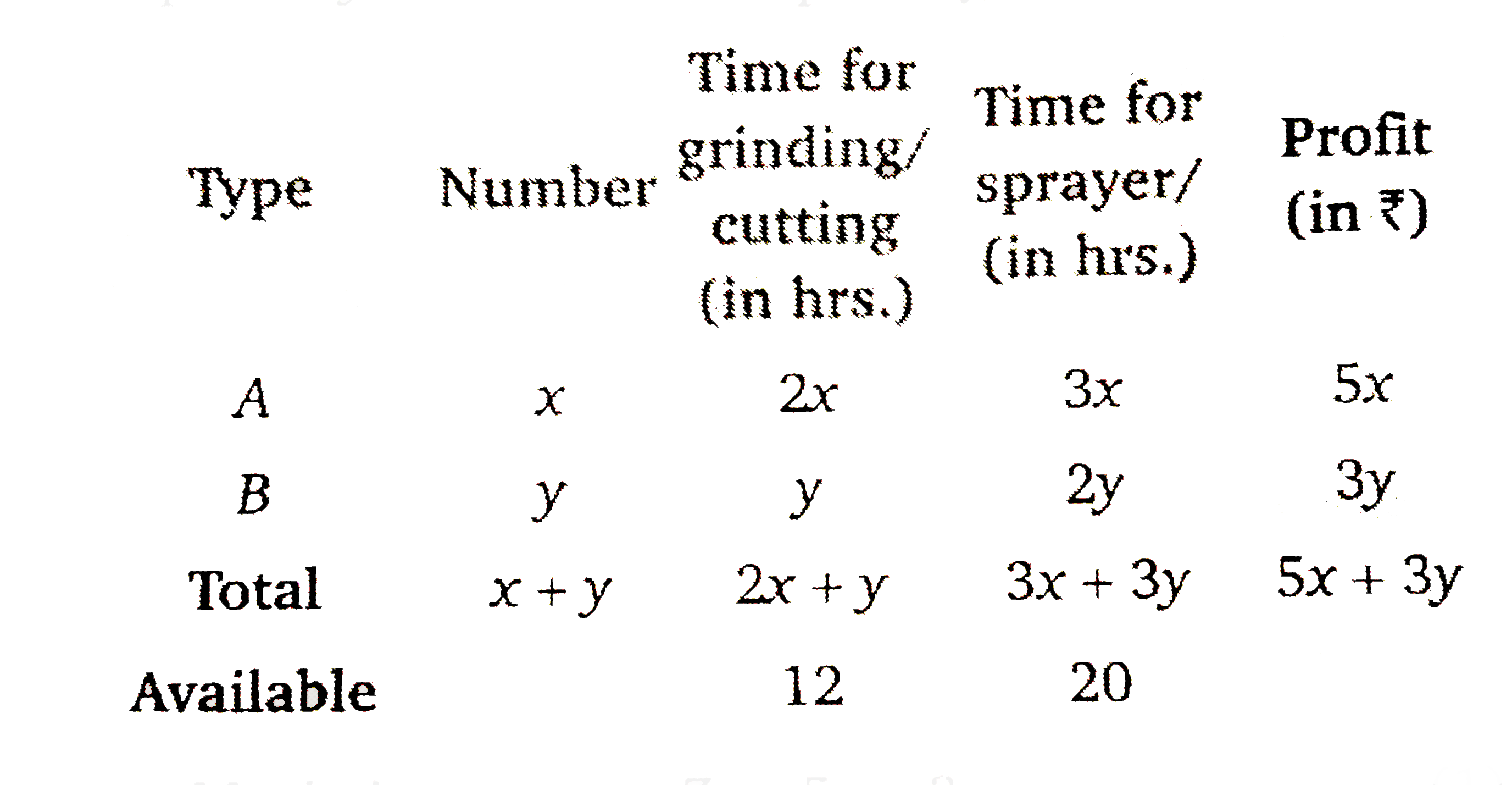

Maximise `Z=5x+3y`…………. 1
Constraints `2x+yle12`…………………2
`3x+2yle20`………………..3
`xge0,yge0`………………….4
First, draw the graph of the equation `2x+y=12`

Put `(0,0)` in the inequation `2x+yle12`,
`2xx0+0le12`
`0le12` (True)
THEREFORE, half plane contain the origin.
Since `x,yge0`
Therefore FEASIBLE region will be in first quadrant.
Now, draw the graph of the line `3x+2y=20`

Put `(0,0)` in the inequation `3x+2yle20`
`3xx0+2xx0le20implies0le20` (True)
Therefore half plane contains the origin.

From equations `2x+y=12` and `3x+2y=20`
The point of intersection is `B(4,4)`
Therefore the feasible region is OABCO.
Its vertices are `O(0,0),A(6,0),B(4,4)` and `C(0,10)` we FIND the value of `Z` at these vertices.

The maximum value of `Z` is Rs. 32 at point `B(4,4),`. Therefore 4 pedestal LAMP and 4 wooden shade should be made the manufacturer to obtain the maximum profit.
Discussion
2228.

If alpha, beta are roots of ax^(2) + bx + c =0 , a cancel(=) 0 and alpha + beta, alpha^(2) + beta^(2) , alpha^(3) + beta^(3)are in G.P. and delta be the discriminant, then :

Answer»

`bc cancel(=) 0`
`B delta = 0`
`C delta = 0 `
`delta = 0 `

Answer :C
Discussion
2229.

y=ae^(x), y=be^(-x) intersect at right angles if ……….. (a ne 0, b ne 0)

Answer»

`a=(1)/(B)`
a = b
`a=-(1)/(b)`
`a+b=0`

ANSWER :A
Discussion
2230.

If A={1,3,5,7,9,11,13,15,17},B={2,4,…..,18} and N is the universal set, then A'uu((A uu B)nn B') is

Answer»

A
N
B
R

Answer :B
Discussion
2231.

Uing cofactors of elements of first row evaluate |{:(2,-1,3),(6,4,16),(8,5,8):}|

Answer»


ANSWER :-182
Discussion
2232.

If x^2 -hx - 21 = 0 and x^2 - 3hx + 35 =0 ( h gt 0) have a common roots, then h =…………..

Answer»

`0`
`1`
`4`
`3`

Answer :C
Discussion
2233.

Find thesmallareaenclosedby thecirclex^2+ y^2 =4 andx+y=2

Answer»


ANSWER :`2 ` SQ UNITS
Discussion
2234.

Integers 1.2.3........n where n gt 2 , are written on a board. Two numbers m, k such that 1 ltm ltn, 1 ltkltnare removed and the average of the remaining numbers is found to be 17. What is the maximum sum of the two removed numbers ?

Answer»


ANSWER :51
Discussion
2235.

If a circle cuts the parabola y^(2)=4ax in four points then the algebraic sum of ordinates of the four points is

Answer»

0
1
-1
none

Answer :A
Discussion
2236.

Find the number of all one-one functions from set A = {1, 2, 3} to itself.

Answer»


SOLUTION :N/A
Discussion
2237.

Let the matrices A=[{:( sqrt3,-2),(0,1):}] and P be any orthogonal matrix such that Q = PAP and let Rne [r_0] _(2-2)=P'Q^(6) Pthen

Answer»

`r_(11) =81 `
`r_(1L) =81 sqrt3`
` r_(11) -4sqrt3`
` r_(11)=-sqrt3`

ANSWER :A
Discussion
2238.

The vertices of Delta ABC are A(2,4) B(-4, 2) and C(0,0). Find the slopes of AC and AB.

Answer»


ANSWER :2, `(1)/(3)` , `45^(@)`
Discussion
2239.

If the coefficients of the r^(th) term and the (r + 1)^(th) term in the expansion of (1 + x)^(20) are in the ratio 1:2, then r is equal to

Answer»

6
7
8
9

Answer :B
Discussion
2240.

Ifa_(0),a_(1),a_(2) ,…, a_(2n) are the coefficients in the expansion of(1 + xx^(2))^(n)in ascending of x show thata_(0)^(2) - a_(1)^(2) - a_(2)^(2) -…+ a_(2n)^(2) = a_(n) .

Answer»

Solution :We have , `(1 + x + x^(2))^(N) = a_(0) + a_(1)x + a_(2)x^(2) + a_(2n) x^(2n)` …(i)
Replacing x by in Eq. (i), we get
` (1 - (1)/(x) + (1)/(x^(2)))^(n)= a_(0) - (a_(1))/(x) + (a_(2))/(x^(2)) - ...+ (a_2n)/(x^(2n))` ...(II)
On multiplyingEqs.(i) and (ii) , we get
`(1 + x + x^(2))^(n)XX (1 - (1)/(x) + (1)/(x^(2)))^(n)= (a_(0) + a_(1)x + a_(2)x^(2)+ ...+ a_(2n)x^(2n) )xx(a_(0) - (a_(1))/(x) + (a_(2))/(x^(2))- ...+ (a_(2n))/(x^(2n)))`
`rArr ((1 + x^(2) + x^(2))^(n))/(x^(2n))= (a_(0) + a_(1)x + a_(2)x^(2)+ ...+ a_(2n)x^(2n) )xx(a_(0) - (a_(1))/(x) + (a_(2))/(x^(2))- ...+ (a_(2n))/(x^(2n)))` ...(iii)
Constant term in RHS ` = a_(0)^(2) - a_(1)^(2) + a_(2)^(2)- ...+ a_(2n)^(2)`
Now, constant term in` ((1 + x^(2) + x^(4))^(n))/(x^(2n) )= `Coefficient of ` x^(2n)`
in ` (1 + x^(2) + x^(4))^(n) = a_(n)` [replacing x by ` x^(2)` in Eq.(i) ]
But Eq.(iii) is an identity , therefore , the constant term in
RHS = constant term in LHS .
`a_(0)^(2) - a_(1)^(2) + a_(2)^(2) - ...+ a_(2n)^(2) = a_(n)`.
Discussion
2241.

Integration using rigonometric identities : (d)/(dx)g(x)=g(x) and g(0)=1 then int g(x)((2-sin 2x)/(1-cos2x))dx....+c

Answer»

`G(X)COTX`
`-g(x)cot x`
`(g(x))/(1-cos2x)`
None of these

Answer :B
Discussion
2242.

int_(1)^(3) (sqrt(3))/(sqrt(4-x)+sqrt(x))dx=

Answer»

1
`1/2`
2
0

Answer :A
Discussion
2243.

The vector with magnitude 17sqrt(2) and in the opposite direction of (0,1,-1) is …………..

Answer»

`17sqrt(2)(0,1,-1)`
`(0,17,-17)`
`(17,17,0)`
`(0,-17,17)`

ANSWER :D
Discussion
2244.

A card is picked at rnadomfrom a pack of 52 playing cards. Given that the picked card is a queen , the probability of this card to be a card of hearts is

Answer»

`1/3`
`4/13`
`1/4`
`1/2`

ANSWER :C
Discussion
2245.

The probability that in a family of 5 children there will be atleast a girl is

Answer»

`(1)/(32)`
`(3)/(32)`
`(29)/(32)`
`(31)/(32)`

Answer :D
Discussion
2246.

{:(Column-I,Column-II),((A)"Number of solution of the equation"sqrt(x+6)=x "is",(P)1),((B)"The number of integral pair"(s)(x,y) "whose sum is equal to",(Q)2),("their product is",),((C)x=(1)/(sqrt(2-3))and y=(1)/(sqrt(2+3))"then the value of" (x-y)^(2)"equals",(R)3),({:("Let" x=1+ ul(""1"")),(""2+ul(""1"")),(""1+ul(""1"")),(""2+ul(" "1"")),(""1+ul(" "1"")),(""2+............):},):}

Answer»

<P>

ANSWER :P,Q,Q,R
Discussion
2247.

Let theequaiton of a ray be |z-2|-|z-1-i| = sqrt(2). If theis strik the y-axis, then the equation of relfected ray (including or excludingthepointof incidence) is .

Answer»

`arg(z-2i)=(pi)/(4)`
`|z-2i|-|z-1-i| = sqrt(2)`
`arg(z-2i)=(3pi)/(4)`
`|z-1i|-|z-1-3i| = 2sqrt(2)`

Solution :INCIDENTRAY is `|z-2|-|z-1-i| = sqrt(2) = |2-(1+i)|`
This ray is EMANATING FORM thepoint '2' and moving totheleft of '2' .
It strikes y-axis at POINT 2i.

Then equation of reflected of reflected ray is `arg(z-2i)=(pi)/(4)`
or `|z-2i|-|z-3-i| = sqrt(2)`
Discussion
2248.

Integrate the function is Exercise. (sin^(-1) sqrt(x)-cos^(-1)sqrt(x))/(sin^(-1) sqrt(x)+cos^(-1) sqrt(x)), x in [0,1]

Answer»


ANSWER :`=(2(2x-1))/(pi) SIN^(-1)X+ (2sqrt (x-x^(2)))/(2)-c`
Discussion
2249.

Solve graphically x + 8y+10>0

Answer»

SOLUTION :
Discussion
2250.

A variable tangent to the parabola y^(2)=4ax meets the parabola y^(2) +4ax=0 at the points P,Q . The locus of the middle point of PQ is

Answer»

`y^(2)+4ax=0`
`y^(2)+2ax=0`
`y^(2)+ax=0`
`3Y^(2)+4ax=0`

ANSWER :D
Discussion