InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 26951. |
1 +1(4.2!) + 1/(16.4!) +1/(64.6!) + ....... = |
|
Answer» `(E-1)/(SQRTE)` |
|
| 26952. |
If the coefficient of x^(7) in [ax^(2) + (1/(bx))]^(11) equals the coefficient of x^(-7) in [ax - (1/(bx^(2)))]^(11), then a and b satisfy the relation |
|
Answer» `a + B = 1` |
|
| 26953. |
Find the equation of tangents of the circle x^(2) + y^(2) - 8 x - 2 2y + 12 = 0at the points whose ordinates are 1. |
|
Answer» |
|
| 26954. |
Evaluate the following integrals int(dx)/(2+3cos2x) |
|
Answer» |
|
| 26955. |
If sinx=(1)/(sqrt(5)),siny=(1)/(sqrt(10))" where "0ltxlt(pi)/(2),0ltylt(pi)/(2),then what is (x+y) equal to ? |
|
Answer» Solution :`SINX=(1)/(sqrt(5)),siny=(1)/(sqrt(10)),0ltxlt(pi)/(2),0ltylt(pi)/(2)` `cosx=sqrt(1-sin^(2)x)"" cosy=sqrt(1-sin^(2)y)` `=sqrt(1(1)/(5))""=sqrt(1-(1)/(10))` `=sqrt((4)/(5))=(2)/(sqrt(5)) ""=sqrt((9)/(10))=(3)/(sqrt(10))`. `sin(x+y)=sinxcosy+cosx siny` `=(1)/(sqrt(5)).(3)/(sqrt(10))+(2)/(sqrt(5))*(1)/(sqrt(10))` `=(5)/(sqrt(5)*sqrt(10))=(sqrt(5).sqrt(5))/(sqrt(5).sqrt(10))=sqrt((5)/(10))=sqrt((1)/(2))=(1)/(sqrt(2))`. `thereforex+y=sin^(-1)((1)/(sqrt(2)))=(pi)/(4)`. |
|
| 26956. |
Let 2 = x + iy, where x and y are real. The points (x, y) in the X-Yplane or which (z+1)/(z-1) purely imaginary lie on |
| Answer» Answer :D | |
| 26957. |
An unbiased die is thrown twice. Let the event A be 'odd number on the first throw' and B the event 'odd number on the second throw'. Check the independence of the events A and B. |
|
Answer» |
|
| 26958. |
Let C : x^(2) -3, D : y = kx^(2) be two parabolas and L_(1) : x a , L_(2) : x = 1 (a ne 0) be two straight lines. If a gt 0, the angle subtended by the chord AB at the vertex of the parabola C is |
|
Answer» `tan^(-1)((5)/(7))` |
|
| 26959. |
If two circles x ^(2) + y ^(2) + 2gx + 2fy =0 and x ^(2) +y ^(2) + 2g _(1) x + 2f _(1) y =0 touch each other, then |
|
Answer» `f_(1) G = f g _(1)` |
|
| 26960. |
Evaluate the following integrals int(dx)/((1+x)sqrt(3+2x-x^(2))) |
|
Answer» |
|
| 26961. |
Prove that : Find the coefficient of x^(6) in (3+2x+x^(2))^(6). |
|
Answer» |
|
| 26962. |
If the point (2 cos theta, 2 sin theta), for theta in (0, 2pi) lines in the region between the lines x+y=2 and x-y=2 containing the origin, then theta lies in |
|
Answer» `(0, (pi)/(2)) uu ((3pi)/(2), 2PI)` |
|
| 26963. |
For each of the differential equations in Exercises 1 to 10, find the general solution: 1.(dy)/(dx) = (1 - cos x)/(1 + cos x) |
|
Answer» |
|
| 26964. |
Given that int e^x[f(x)+f^'(x)] dx = e^x f(x)+c. By writing int e^x(sinx+cosx)dx = int e^x sinxdx+ int e^x cosx dx and applying integration by parts in the first integral, evaluate int e^x(sinx+cosx)dx |
|
Answer» SOLUTION :`INT e^X(sinx+cosx) dx = e^x sinx+c` `int e^x (F(x)+f^.(x)) dx = e^x f(x)+c` |
|
| 26965. |
Let the incircle with center I of DeltaABC touch sides BC, CA, AB at D,E and F, respectively. Let a circle is drawn touching ID, IF and incircle of DeltaABC having radius r_(2). Similarly r_(1) and r_(3) are defined. Prove that (r_(1))/(r -r_(1)) .(r_(2))/(r-r_(2)) .(r_(3))/(r-r_(3)) = (a + b+c)/(8R) |
Answer» SOLUTION : From the figure, in `Delta IQP` `cos.(B)/(2) = (PQ)/(IP)` Since `PQ = r_(2)` and `IP = r - r_(2)` (as two circles TOUCHING internally), we have `cos.(B)/(2) = (r_(2))/(r-r_(2))` SIMILARLY, for other such circles, `cos.(A)/(2) = (r_(1))/(r -r_(1)) and cos.(C)/(2) = (r_(3))/(r -r_(3))` `(r_(1))/(r -r_(1)) .(r_(2))/(r -r_(2)) .(r_(3))/(r -r_(3)) = cos.(A)/(2) cos.(B)/(2) cos.(C)/(2)` `= (1)/(4) (sin A+ sin B + sin C)` `= (a + b + c)/(8R)` |
|
| 26966. |
Prove the following overset((pi)/(4)) underset(0) int 2 tan^(3)x dx=1- log 2 |
|
Answer» |
|
| 26967. |
Evaluate the following integrals intsqrt((5-x)/(x-2))dx |
|
Answer» |
|
| 26968. |
Find the range of the following functions f(x) = log_e (sinx^(sinx) + 1) where 0 lt x lt pi//2. |
|
Answer» |
|
| 26969. |
Express the following as trigonometric ratios of some acute angles.sec 380^@ |
| Answer» SOLUTION :`SEC 38^@ = sec (360^@+20^@) = sec 20^@` | |
| 26970. |
The set of all real x satisfying the inequality (3-|x|)/(4-|x|) ge 0 is |
|
Answer» `[3,3] UU (-OO, -4) uu (4,oo)` |
|
| 26971. |
lim_(x to 0) ((2^x +3^x + 6^x )/3)^(3//x) is equal to : |
|
Answer» `L=E^("LIM"_(x to 0)) (2^x log 2+3^x log 3+6^x log 6)/1` `L=e^(log (2xx3xx6)) = e^(log 36) =36` |
|
| 26972. |
From the set of numbers {2,3,4,…..,30} a number is selected at random. If it is a composite number it is divided by 5 other wise it is divided by 3. The probability that the remainder is zero is |
| Answer» Answer :A | |
| 26973. |
If (1)/(2xx4)+(1)/(4xx6)+(1)/(6xx8)+…. (n terms) =(kn)/(n+1), then k is equal to |
| Answer» ANSWER :A | |
| 26974. |
Find the second order derivatives of the functions given in Exercises 1 to 10. x^(3) log x. |
|
Answer» |
|
| 26975. |
If a variable line in two adjacent positions has direction cosines l, m, n and I + deltaI, m + deltam, n + deltan, then show that the small angle delta theta between the two positions is given by delta theta^2=deltal^2+deltam^2+deltan^2. |
|
Answer» |
|
| 26976. |
If the median and the range of four numbers a,b,2a+b,a-bwhere 0 lt blt a lt 2b ,are 15 and 42, the standard deviation of a and b , is |
|
Answer» |
|
| 26977. |
A ferry boat travels from a dock on the mainland toward an island , stops to discharge and load passengers, then returns to the mainland dock . Among the following graphs, which one best represents the relationship between the distance , in kilometers , of the ferry from the island and the time, in minutes, from when the ferry leaves the mainland dock until it returns ? |
|
Answer»
|
|
| 26978. |
Solve the following system of linear equations by matrix method. x-y+2z=7 3x+4y-5z=-5 2x-y+3z=12 |
|
Answer» |
|
| 26979. |
lim_(x rarr 2^(+)) (([x]^(3))/(3) - [(x)/(3)]^(3)) equals : |
| Answer» Answer :C | |
| 26980. |
If A(3,4) and B(-5,-2) are the extremities of the base of an isosceles triangle ABC with tan C = 2, then point C can be |
|
Answer» `((3sqrt(5)-1)/(2),-(1+2sqrt(5)))` 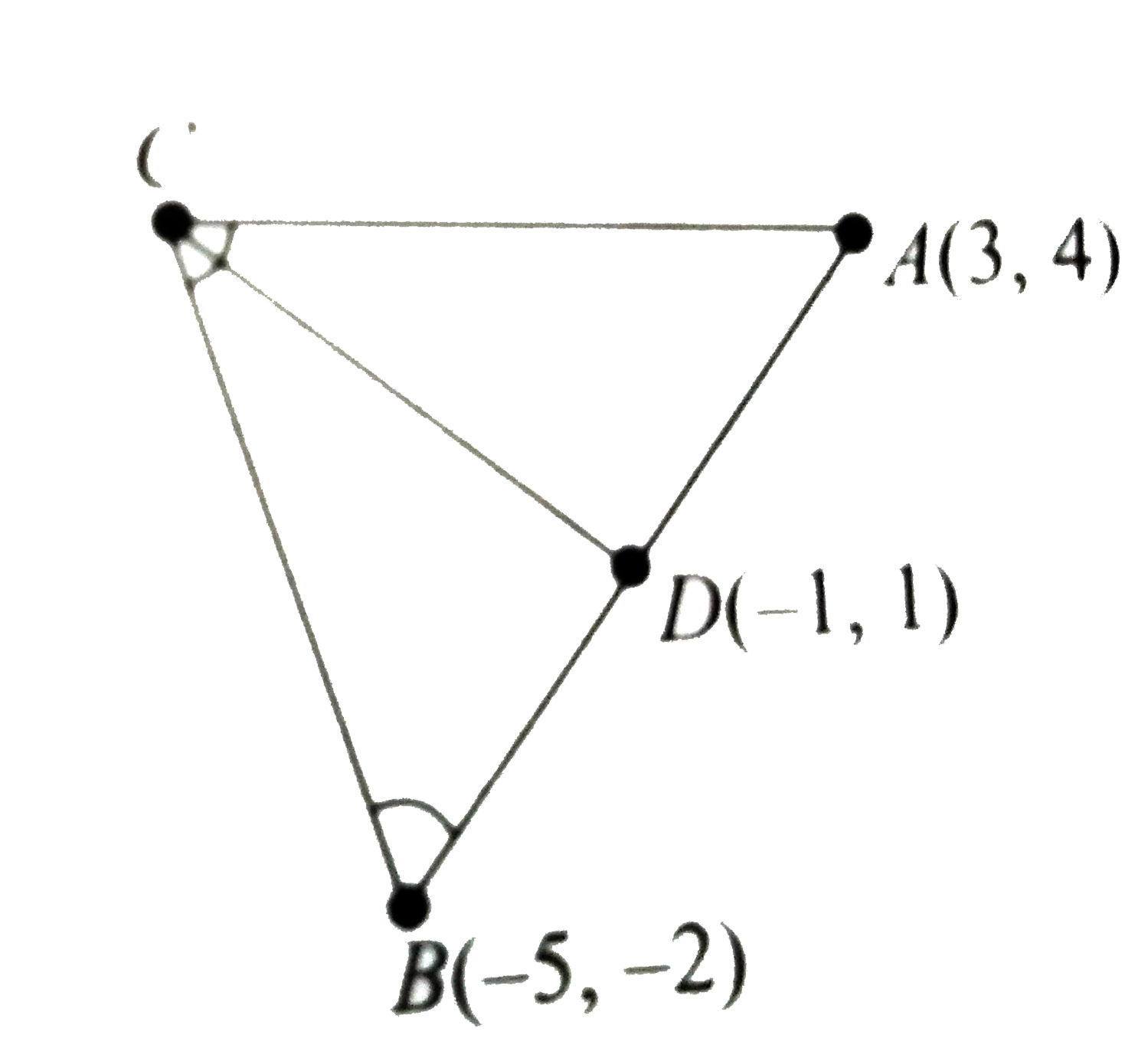 `D(-1,1)` is midpoint of AB. `CD = BD cot.(C)/(2) =5. cot.(C)/(2)` Now, `tan C = 2` `rArr (2tan.(C)/(2))/(1-tan^(-2).(C)/(2)) =2` `rArr tan^(2).(C)/(2) +tan.(C)/(2)-1 =0` `rArr tan.(C)/(2) =(-1+sqrt(5))/(2)` `rArr cot.(C)/(2) =(sqrt(5)+1)/(2)` `rArr CD = 5 ((sqrt(5)+1)/(2)) =(5)/(2) (sqrt(5)+1)` Slope of BD is `3//4`. `:.` Slope of CD is `-4//3 = tan ALPHA` Using parametric FORM of straight line, coordinates of C are given by `(-1+-(5(sqrt(5)+1))/(2)cos alpha,1+-(5(sqrt(5)+1))/(2)sin alpha)` or `(-(5+3sqrt(5))/(2),2sqrt(5)+3)` and `((3sqrt(5)-1)/(2),-(2sqrt(5)+1))` |
|
| 26981. |
x^(2)+y^(2)-4x-4y+7=0 and x^(2)+y^(2)4x+4y+7=0 are equation of excircleopposite to B and C respectively in a DeltaABC, then |
|
Answer» `A = (0,0)` `O_(2)=(-2,-2),r_(2)=1` `impliesA=(0,0)` |
|
| 26982. |
Evaluate the following definite integrals : int_(0)^(1)(dx)/(x^(2)+x+1) |
|
Answer» |
|
| 26983. |
If P_(1),P_(2),P_(3) are altitudes of DeltaABC from the vertices A,B,C and Delta is the area of triangle then,1/P_(1)^(2)+1/P_(2)^(2)+1/P_(3)^(2) = |
|
Answer» `a^(2)+B^(2)+C^(2)/4Delta^(2)` |
|
| 26984. |
The parabola y=4-x^(2) has vertexP. It intersects x-axis at A and B. If the parabola is translated from its initial position to a newposition by moving its vertex along the line y=x+4, so that it intersects x-axis at B and C, then abscissa of C will be : |
|
Answer» 3 |
|
| 26985. |
A compound possesses 8% sulphur by mas. The least molecular mass is :- |
|
Answer» 200 |
|
| 26986. |
Find dy/dx if y = x cot^(-1) (x/y) |
|
Answer» 1992 |
|
| 26987. |
For the curve sqrtx + sqrty=1, (dy)/(dx) " at " ((1)/(4), (1)/(4)) is ………. |
|
Answer» |
|
| 26988. |
Evalute the following integrals int (1)/((2x + 3)sqrt(x + 2)) dx |
|
Answer» |
|
| 26989. |
If f(x) =x for x lt 0 =0 for x=0 =x^(2)"for "x gt 0" then "underset(x to 0)"Lt" f(x)= |
|
Answer» `-1` |
|
| 26990. |
If A=[(2,1,1),(1,0,1),(0,2,-1)],find the inverse of A, using elementary row transformations and hence solve the equation XA=["101"]. |
|
Answer» |
|
| 26991. |
A hyperbola has axes along the coordinate axes. Its trasverse axis is 2a and it passes through (h.k). Find its eccentricity. |
|
Answer» |
|
| 26992. |
A card from a pack of 52 cards is lost. From the remaining cardsof the pack, two cards are drawn and are found to be both spades. Find the probability of the lost card being a spade. |
|
Answer» <P> Solution :Let `E_1,E_2,E_3and E_4` be the events of losing a card of SPADES, clubs, hearts and diamonds repectively.Then, `P(E_1)=P(E_2)=P(E_3)=P(E_4)=13/52=1/4.` Let E be the event of drawing 2 spades from the remaining 51 cards. Then, `P(E//E_1)`= PRBABILITY of drawing 2 spades, given that a card of spades is missing `(.^12C_2)/(.^51C_2)=((12xx11))/(2!)XX(2!)/((51xx50))=22/425` `P(E//E_2)`=probability of drawing 2 spades, giventhat a card of clubs is missing `(.^13C_2)/(.^51C_2)=((13xx12))/(2!)xx(2!)/((51xx50))=26/425` `P(E//E_3)`= probability of drawing 2 spades, given that a card of hearts is missing `=(.^13C_2)/(.^51C_2)=26/425`. `P(E//E_4)`= probability of drawing 2 spades, given that a card of diamonds is missing `=(.^13C_2)/(.^51C_2)=26/425`. `:. P(E_1//E)`= probability of the lost card being a spade, given that 2 spades are drawn from the remaining 51 cards `(P(E_1).P(E//E_1))/(P(E_1).P(E//E_1)+P(E_2).P(E//E_2)+P(E_3).P(E//E_3)+P(E_4).P(E//E_4))` `=((1/4xx22/425))/((1/4xx22/425)+(1/4xx26/425)+(1/4xx26/425)+(1/4xx26/425))` Hence, the required probability 0.22. |
|
| 26993. |
Find the centre of the circle passing through the points (0,0), (2,0) and (0, 2). |
|
Answer» |
|
| 26995. |
Examine the continuity of the function f(x)= 2x^(2) -1 " at " x=3 |
|
Answer» |
|
| 26996. |
f(x) = (x^(3) + x^(2) - 16 x + 20)/((x - 2)^(2)) " if" x ne 2 , = kif x = 2 , f(x) is continuous at x = 2 then |
|
Answer» 5 |
|
| 26998. |
Find the approximate value of each of the following :(15.5)^((1)/(4)) |
|
Answer» |
|
| 26999. |
The remainder when 3^(100)xx22^(50) is divided 5 is |
|
Answer» 3 |
|
| 27000. |
An arithmetical progression has positive terms. The ratio of the differrence of the 4^(th) and the 8^(th) term to 15 ^(th) term is (4)/(15) and the square of the difference of the 4^(th) and the 1 ^(st) term is 225. Which term of the series is 2015 ? |
|
Answer» |
|