InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 27451. |
Find the values of the following : tan^(-1)(tan frac (3pi)4) |
|
Answer» SOLUTION :`COS^(-1)(cos FRAC(13pi)6)=cos^(-1)(cos(2pi+pi/6))` `cos^(-1)(cosfracpi6)=pi/6` |
|
| 27452. |
int sin ^(-1) sqrt(-x/(a+x))dx= |
|
Answer» `COSEC ^(-1)(sqrt(X/(a+x)))(x/a)+ax+C` |
|
| 27453. |
The projection of (1, 2, -1) on hati is ……………. |
|
Answer» `(1)/(SQRT(6))` |
|
| 27454. |
SOLVE : y (dy)/(dx) = 1 |
| Answer» | |
| 27455. |
Find the number of ways of forming a committee of 5 members out of 5 men and 5 women so that in the committee there is atleast one man |
|
Answer» |
|
| 27456. |
Let f be a continuous function [a, b] such that f(x) gt 0 for all x in [a,b]. If F(x) = int_(a)^(x) f(t) dt then |
|
Answer» F is differentiable but not increasing on [a, B] |
|
| 27457. |
Find the number of ways of forming a committee of 5 members out of 5 men and 5 women so that in the committee women will be in a majority |
|
Answer» |
|
| 27458. |
E and F are mid-points of sides of AD and BCrespectively of quadrilateral ABCD having vertices A(1, 2, 1), B(-2, 4, -1), C(-1, 3, 2), D(5, -1, 6), then |
|
Answer» EF is parallel to AB |
|
| 27459. |
Let g be a differentiable function satisfyingint_(0)^(x)(x-t+1)g(t)dt=x^(4)+x^(2) for all x ge 0 . If the value of int_(0)^(1)(12)/(g'(x)+g(x)+10)dx is equal to k pi thenis equal to: |
|
Answer» |
|
| 27460. |
Find adjoint of each of the matrices [{:(2,-1,3),(4,2,5),(0,4,1):}] |
|
Answer» |
|
| 27461. |
Find the absolute value of (tanAtan2A)+(tan2A tan4A)+(tan4A tanA) where A=(2pi)/7. |
|
Answer» |
|
| 27462. |
Using differentials, find the approximate value of each of the up to 3 places of decimal. sqrt(49.5) |
|
Answer» |
|
| 27463. |
Choose the correct answer The value of int_(0)^(pi/2)log((4+3sinx)/(4+3cosx))dx is |
| Answer» Answer :C | |
| 27464. |
A firm knows that demand function for its main product is linear. It also knows that it can sell 3000 units at ₹ 5 per unit and it can sell 1200 units when price is ₹ 11per unit. Find the demand function. |
|
Answer» |
|
| 27465. |
Let f,[k,k+1,….,2007]to[1,2,3, …..,n] be defined by f(x)=[2007/x] (where [.] denotes the greatest integer function). The maximum value of k/10 such that it is not possible to make f an onto function for any vale of n is _______ |
|
Answer» |
|
| 27466. |
The probability of getting quallifed in IIT JEE EAMCET by student are respectively 1/5 " and " 3/5. The probability that the student gets qualifed for at least one of these tests, is |
|
Answer» `(3)/(25)` |
|
| 27467. |
If |{:(1,cos alpha, cos beta),(cos alpha, 1 , cos gamma ),(cos beta, cos gamma , 1):}|=|{:(0,cos alpha, cos beta),(cos alpha , 0 , cos gamma),(cos beta, cos gamma, 0):}| then the value of cos^2 alpha + cos^2 beta + cos^2 gamma is : |
|
Answer» 1 |
|
| 27468. |
Given that the slope of the tangent to a curve y = y(x) atany point (x,y) is (2y)/x^(2) If the surve passes through the ltbegt centre of the circle x^(2) +y^(2) - 2x -2y =0, then itsequation is(a) x^(2)log_(e)absy =-2(x-1)(b) xlog_(e)absy = x-1(c) xlog_(e)absy =2(x-1)(d) xlog_(e)absy =-2(x-1) |
|
Answer» (a) `x^(2)log_(e)absy =-2(x-1)` `rArrint dy/y= int (2)/x^(2)dx`[integrating both sides] `rArrlog_(e abs(y))=-2/x+C…(i)` Since, curve (i) passes through centre (1,1) of the circle `x^(2)+y^(2)-2x-2y=0` `thereforelog_(e)(1)=-2/1+CrArr C=2` `therefore` Equation required curve is `log_(e) abs(y)=2/x+2`[put C=2 in Eq. (i)] `rArrxlog_(e) abs(y)=2(x-1)` |
|
| 27469. |
If A{:[(7,6,-1),(4,2,3),(1,3,0)]:}={:[(4,2,3),(1,2,0),(7,6,-1)]:} then A= |
|
Answer» `{:[(1,0,0),(0,0,1),(0,1,0)]:}` |
|
| 27470. |
y and z are ............ |
Answer» 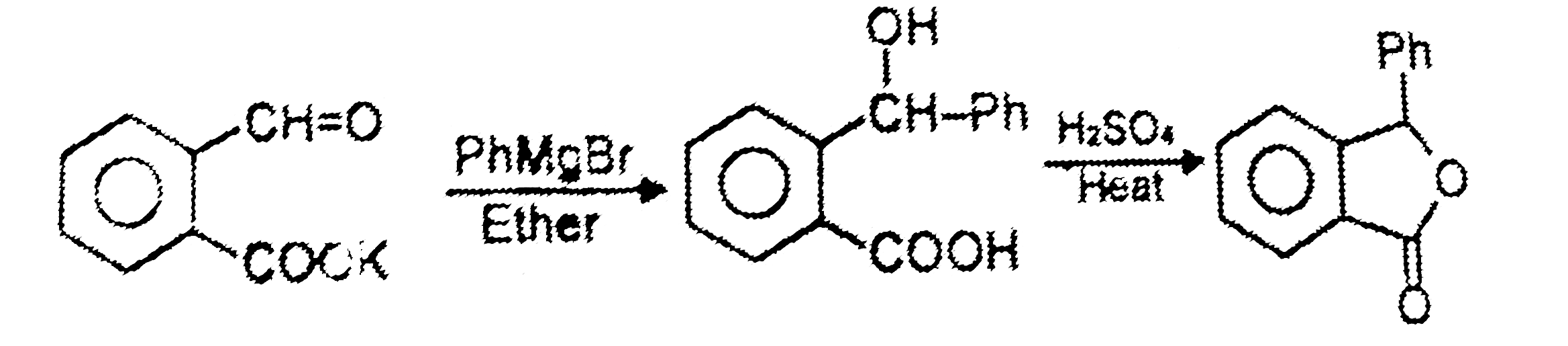 Step-1 is nucleophilic addition of GRIGNARD REAGENT and step-2 is esterification reaction. |
|
| 27471. |
If a function of defined by f(x) = {((1-sinzx)/(pi-2x), ",","if" x != pi/4),(k, ",", "if" x = pi/4):} is continuous at x = (pi)/4, then k = |
| Answer» ANSWER :A | |
| 27472. |
If the regrassioncoefficient of Y on X is 1.6 that of X on Y is 0.4 , andthetabe the angle between two regression lines , find the value oftan theta |
|
Answer» |
|
| 27473. |
The number of ways in which 21 objects can be grouped into three groups 8, 7 and 6 object is |
|
Answer» 455 |
|
| 27474. |
I. The locus of the point from which the length of the tangents to the two circles x^(2)+y^(2)+4x+3=0, x^(2)+y^(2)-6x+5=0 are in the ratio 2:3 is a circles with centre (-6,0) II. The length of the chord x=3y+13 of the circle x^(2)+y^(2)-4x+4y+3=0" is "sqrt10. |
|
Answer» only I is true |
|
| 27475. |
When a right handed rectangular Cartesian system OXYZ rotated about z-axis through pi//4 in the counter clock wise sense it is found that a vector vecr has the components 2sqrt(2),3sqrt(2) and 4. The components of veca in the OXYZ coordinate system ar |
|
Answer» `5,-1,4` |
|
| 27476. |
Find the values of k so that the function f is continuous at the indicated point f(x) = {((sqrt(1+ kx)-sqrt(1-kx))/(x)",","if " -1 le x lt 0),((2x+1)/(x-1)",","if " 0 le x lt 1):} at x= 0 |
|
Answer» |
|
| 27478. |
Evaluate the integrals . underset(0)overset(pi//2)int (sin^(5)x)/(sin^(5)x + cos^(5)x)dx |
|
Answer» |
|
| 27479. |
Arealyingin the firstquadrant andboundedby thecirclex^2 +y^2 =4and thelinex=0andx=2 is |
|
Answer» `PI` |
|
| 27480. |
Let f(a,b) = int_(a)^(b)(x^(2)-4x+3)dx, (bgt 0) then |
|
Answer» `f(a,3)` is LEAST when `a = 1` |
|
| 27481. |
Evaluate int_(0)^(n) [x] dx, (n in N) where [ ] denotes the GIF |
|
Answer» |
|
| 27482. |
10C_1= |
|
Answer» ` |
|
| 27483. |
If the equations 2x-lambday+5z=7 and lambda x-8y-10z+14=0 represent the same plane then lambda is : |
| Answer» Solution :N/A | |
| 27485. |
Let F_1(x_1,0) and F^(2)(x_2,0) for x_1lt0 andx_2gt0, be the foci of the ellipse x^(2)/9+y^(2)/8=1. Suppose a parabola having vertex at the origin and the focus at F_2intersects the ellipse at point M in the first quadrant and at point N in the fourth quadrtant.Q. The eccentricity of an ellipse whose center is at the origin is 1/2. If one of its directices is x=-4, then the equation of the normal to its (1,3/2) is |
|
Answer» `x+2y=4` |
|
| 27486. |
Integrate the function in Exercise. x sin 3x |
|
Answer» |
|
| 27487. |
int (x - "sinx")/(1 -cosx) dx = |
|
Answer» `X COT""(x)/(2) + C ` |
|
| 27488. |
{:("column - I" , "Column II"), ("(A) The number of integral solutions of the inequality " ((x-1)^(2)(x-4)^(3)(x-7))/((x-2) (x-6)) le 0 " is/are", "(p)" 1),("(B) The integral values that the function " f(x) = sqrt(x-2) + 2sqrt(6-x) " can take is/are" , "(q)" 2),( "(C) Let f"D to Rand f(x) =underset(" n times")(InInIn..In)(x^(2) -x/2 + 49/16 + cos4 pi x) " then the value/s of n for which f is onto is/are", "(r)" 3),("(D)If f(x) is continuous and differentiable function " AA xx in R and " f (c)= 0 for exactly 2 real valuesof c thenthe number of real values of d for which f(d) = 0 can be", "(s)" 4):} |
|
Answer» (II), (III) , (Q) |
|
| 27489. |
Find the area enclosed by y=e^x,x=0,y=2,y=3 |
|
Answer» Solution :Given CURVE is `y=e^x` They x= In y Area = `int_2^3xdy=int_2^3 Inycdotdy` `[In ycdoty]_2^3-int_2^3 1/ycdotydy=[Inycdoty]_2^3-int_2^3 1/ycdotydy` = (3 In 3 - 2 In 2) - `[y]_2^3` `In 3^3/2^2 -(3-2)=In27/4-1` |
|
| 27490. |
A radioactive substance decompose at a rate proportional to the quantity of thesubstance present. Ifintiallythe substance present is 100 mg and the half life of substance is 1590 years, then the substance reduces to 30 mg in log((10)/(3))=1.2040,log2=0.6932 |
|
Answer» 2761.62 years |
|
| 27492. |
A man in a boat rows 3 miles off along straight shore and wants to reach a point 4 miles up the shore on the opposite side. If he can row 2 miles/hour and walk 4 miles/hour, describe his fastest route. |
|
Answer» |
|
| 27493. |
Let f(x)be continuous on [a,b], differentiable in (a,b) and f(x)ne0"for all"x in[a,b]. Then prove that there exists one c in(a,b)"such that"(f'(c))/(f(c))=(1)/(a-c)+(1)/(b-c). |
| Answer» | |
| 27494. |
int e^(sinx).sin2x dx = |
|
Answer» `2e^("SINX")`(sinx + 1) + C |
|
| 27495. |
if the rate of a sphere increasing at the rate of 0.4 cm //sec, then, when the radius is decimetres , its surface area is increasing at the rate of |
|
Answer» `160 pi CM ^(2) //sec`. |
|
| 27496. |
An alpha-particle of mass m suffers 1-dimentinal eleastic collision with a nucleus at rest of unknown mass. It is scattered directly backwards losing 64% of its initial kinetic energy. The mass of the nucleus is : |
|
Answer» 2 m |
|
| 27497. |
If a,b,c are all different and |(1+a^(2),1+b^(2),1+c^(2)),(a,b,c),(a^(3),b^(3),c^(3))|=0 then a+b+c= |
|
Answer» 0 |
|
| 27498. |
If A,B are two events such that P(A)=0.3, P(B)=0.4,P(AcupB)=0.6 Find P(A | B) |
|
Answer» SOLUTION :A and B are two SET EVENTS such that P(A)=0.3,P(B)=0.4, P`(AcupB)`=0.6 We have `P(A cup B)=P(A)+P(B)-P(A CAP B)` or, 0.6=0.3+0.4-P`(A cap B)` `P (A | B)=(P(A cap B))/(P(B))=0.1/0.4=1/4` |
|
| 27499. |
For the plane II = 4x - 3y + 2z - 3=0, the points A (-2, 1, 2) B = (3, 1, -2) |
|
Answer» lie on the same SIDE of `prod = 0` |
|
| 27500. |
int(1+cos x)/(x+sinx)dx=....+C |
|
Answer» `log|1+cosx|` |
|