28278 + Interview Questions in Maths in Class 12 Page 552 InterviewSolution

27551.	If two vertical towers PQ and RS of lengths a and b (a gt b) respectively subtend the same angle alpha at a point A on the line joining their feet P and R in the horizontal plane and angles beta and gamma at another point B on this line nearer the towers on the same side of the towers as A, then (sin (beta - gamma))/(sin(beta - alpha)) is equal to
Answer» `(B SIN ALPHA)/((a-b) sin GAMMA)` `((b-a)sin gamma)/(b sin alpha)` `(sin gamma)/(sin alpha)` `((b-a)sin alpha)/(b sin gamma)` ANSWER :B

Discussion

27552.	Write{1,3,9,27)set in the intention(or specification form).
Answer» SOLUTION :`{x:x =3^N n INZ, 0 le n le 3}`

Discussion

27553.	Evalute: int((1+logx)^2)/(x)dx
Answer» ANSWER :`1/3(1+logx)^(3)+C`

Discussion

27554.	Using elementary transformations, find the inverseof the matrices [(2,1),(1,1)]
Answer» ANSWER :`[(1,-1),(-1,2)]`

Discussion

27555.	Find the derivative (dy)/(dx)of functions represented parametrically : (a)x = int_(2)^(1) (I n z)/( z) dz, y = int_(5)^(I n t) e^(z) dz (b)x = int_(c^(2))^(sin t) " arc sin z dz, " y = int _(n)^(sqrt(t)) (sin z^())/(z) dz
Answer» ANSWER :(a)`y_(X) = (t)/(In t )` (B)`y_(x) = (TAN t)/( t^(2))`

Discussion

27556.	Designed by Dumbledore himself, this round was supposed to be the most adventurous. The objective of the event was to infiltrate a secure location( code named VIENNA)in Hogwarts and to secure your best friend who has been trapped there. You have to exit the location through the tunnel networks whose blueprint is given below. As seen in the picture there are 5 tracks ( Green, Brown, Red, Violet, Yellow). The time taken to travel between 2 junctions along the respective lines is given below. Green – 5 mins, Brown – 4 mins, Violet – 3 mins, Yellow – 2mins, Red- 1 min. Harry will start from the left end of the green track and his aim is to reach the right end of the Red/Violet/Yellow Track as quickly as possible Red: .................... Brown: ......................... Yellow: ____________________ Violet_____________ Green: ____________ But each track has 2 guards starting from each end of the track except for green track( has only one guard starting from the right end). The guards take two minutes to travel between any two junctions( intersecting points between tracks are junctions not thebending points) and wait for 30 seconds at each junction. Guards will change their direc- tion once they reach the end of their track. The guard and the player should not move across each other at any instant of time.The player cannot reuse the paths between junctions i.e each path cannot be used more than once. Note that if you enter a junction at time x and the guard leaves that junction at the same time then you are not caught.What is the time taken by Harry if he reaches as soon as possible ?
Answer» Solution :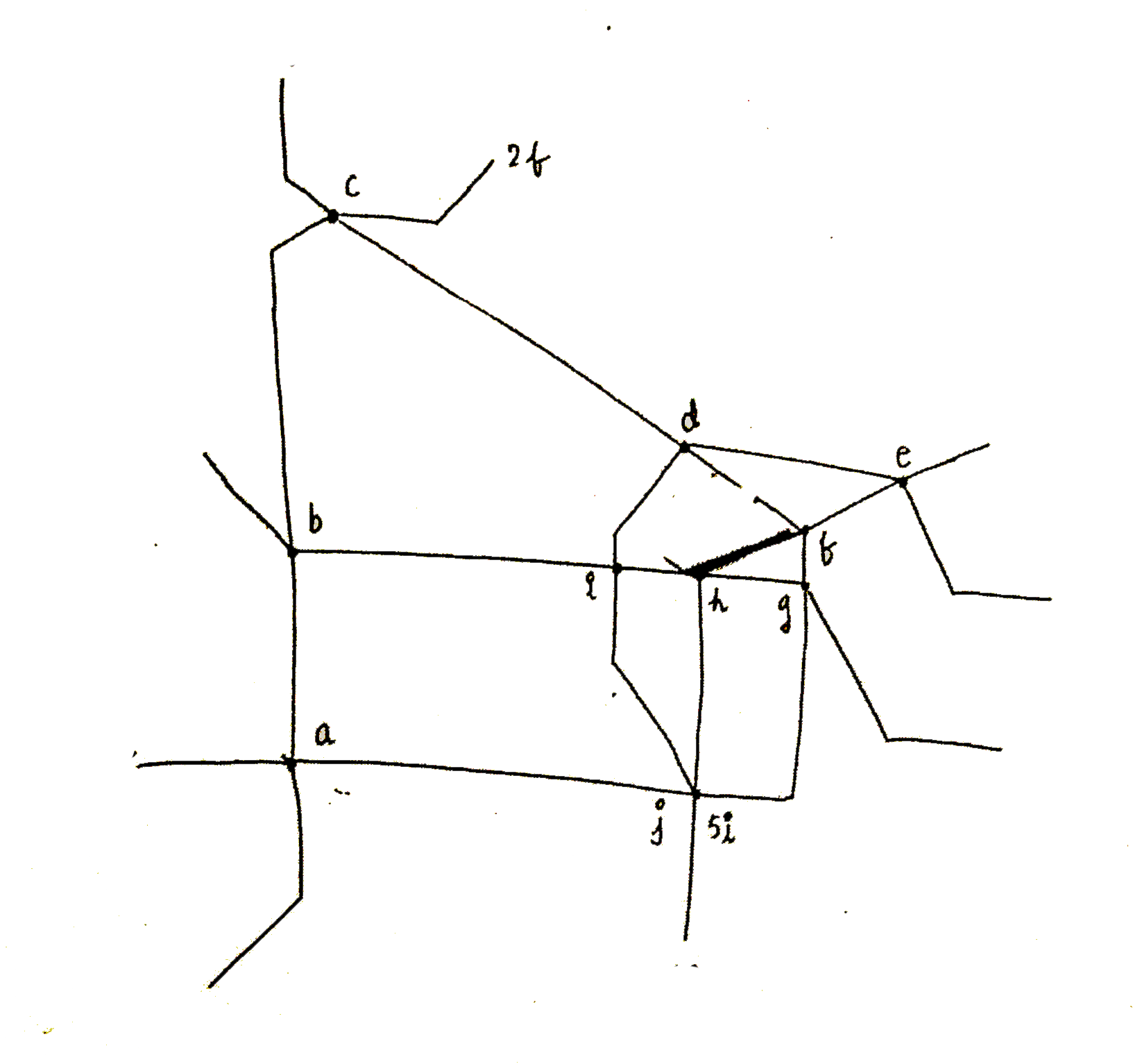 Mone1: `1_(i) rarr a` Time elapsed - 5 mins Time taken - 5 mins Guards will be learning : 1: (d) 2: (b,b) 3, (I,h) 4: (h,g) 5: (d,d) Mone 2: `a rarr j` Time elapsed = 10 mins Now, all come their junctions. The agent doesn't get caught (at j) as the guard lenes as he enters the junctions. Guards will be learning: 1:(g) 2: (2f,2i) 3: (g,b) 4:(e,J) 5: (5f, 5i) Mone 3: `j rarr h` 2 mins `larr` time taken `h rarr f` Time elapsed : 12 mines Now, 2 does not mater anyone (self-explantry)As only 2 more mins have elapsed the guards will be starying at the following stops (for 30 more seconds) 1: (J) 3: (3f, 3I) 4: (4f, 4i) 5: (e,i) Mone `4 : f rarr e` 1 MIN `larr` time taken Time elapsed : 13 min Now the guards are in motion as follows- `1: (J rarr a) 2: (3f rarr g, 3irarr b) 4: (4f rarr e, 4i rarrJ) 5: (e rarr d, i rarr d)` At this point, the game becomes very close.one final monu : `e rarr 5f rArr` and game ones (3 mines) TOTAL times taken : 16 mins

Discussion

27557.	There are 100 stations between two stations A and B. A train is to stop at ten of these 100 stations. What is the probability that no two of these ten stations are consecutive.
Answer» ANSWER :`(.^(91)C_(10))/(.^(100)C_(10))`

Discussion

27558.	Ifveca=hati+hatj+hatk,vecb=hati+hatj, vecc= veciand(vecaxxvecb))xxvecc=lambdaveca+muvecbthen the value oflambda + muis._______
Answer» 0 1 6 3 Answer :A

Discussion

27559.	If f2f(x) +3f (-x) =x^(2) -x+1, then the value of f'(1) is-
Answer» `7/5` `5/7` `6/7` `7/6` ANSWER :A

Discussion

27560.	Find the area bounded by curves (x - 1)^(2) + y^(2) = 1" and "x^(2) + y^(2) = 1.
Answer» ANSWER :`((2PI)/(3) -sqrt3/2)`

Discussion

27561.	If x_(1), x_(2), x_(3), x_(4) are positive roots of the equation x^(4)-8x^(3)+ax^(2)-bx+16=0 then tan^(-1)(x_(1))+tan^(-1)(x_(2))+tna^(-1)(x_(3))+tan^(-1)(x_(4)) can be equal to
Answer» `pi+4 TAN^(-1)(2)` `4 tan^(-1)(2)` `pi-4tan^(-1)(2)` none of these Answer :B

Discussion

27562.	Solve the inequation \|a^(2x)+a^(x+2)-1\|ge1 for all values of a(agt0,a!=1)
Answer» Solution :Using `a^(x)=t` the GIVEN inequation can be WRITTEN in the form `\|t^(2)+a^(2)t-1\|ge1`…i `:'agt0` and `a!=1` then `a^(x)gt0` `:.tgt0` ………ii Inequation (i) write in the forms `t^(2)+a^(2)t-1ge1` and `t^(2)+a^(2)t-1le-1` `:.tle(-a^(2)-sqrt(a^(4)+8)/2,tge(-a^(2)+sqrt((a^(4)+8)))/2` and `-a^(2)letle0` But `tgt0` [from Eq (ii)] `:.tge(-a^(2)+sqrt((a^(4)+8)))/2` `:.a^(x)ge(-a^(2)+sqrt((a^(4)+8)))/2` For `0ltalt1` `xlelog_(a)((-a^(2)+sqrt(a^(4)+8)))/2)` `:.x epsilon[-oo,log_(a)((-a^(2)+sqrt((a^(4)+8)))/2)]` and for `agt1,xgelog_(a) ((-a^(2)+sqrt((a^(4)+8)))/2)` `:.x epsilon(log_(a)((-a^(2)+sqrt((a^(4)+8)))/2),oo)`

Discussion

27563.	Differentiate the functions given in Exercises 1 to 11 w.r.t. x. 2^(sin x).
Answer» Answer :`2^(sin X)cos x LOG 2`

Discussion

27564.	A man of height 2 metres walks at a uniform speed of 5 km/h away from a lamp post which is 6 metres high. Find the rate at which the length of his shadow increases.
Answer» ANSWER :`(5)/(2)` km/hour

Discussion

27565.	int(sinx + cos x) dx
Answer» ANSWER :`-COSX + SINX + C`

Discussion

27566.	If 7x-2lt 4 - 3x and 3x-1 lt 2 + 5x, then x lies in the interval
Answer» `(3/5 ,3/2)` `(-3,2 ,3/5)` `[-3/2 , 3/5)` `[-3/2 , 3/5]` ANSWER :B

Discussion

27567.	f(x) is a strictly increasing function, iff'(x) is........a)Positive b)Negative c)0 d)None of these
Answer» Positive Negative 0 None of these Answer :A

Discussion

27568.	BagI contains 3 red and 4 black balls while another Bag II contains 5 red and 6 black balls. One ball is drawn at random from one ofthe bags and it is found to be red. Find the probability that it was drawn from Bag II.
Answer» ANSWER :`(35)/(68)`

Discussion

27569.	Choose a number n uniformly at random from theset {,2,.....,100} . Choose one ofthe first seven days of the year 2014 at random and consider n consecutive days starting from thechosen day what is the probability that among the chosen n days, the number of Sundays isdifferent from the number of Mondays?
Answer» `(1)/(2)` `(2)/(7)` `(12)/(49)` `(43)/(175)` SOLUTION :N//A

Discussion

27570.	A point (x,y,z) moves parallel to xy-plane. Which of the three variables x,y,z remains fixed? (A) x and y (B) y and z (C) z and x (D) none of these
Answer» x y and z x and y z and x Answer :B

Discussion

27571.	Let y be an implicit functio of x defined by x ^(2x) - 2x ^(x) cot y-1 =0. Then y'(1) equals
Answer» 1 LOG 2 `-log 2` `-1` ANSWER :D

Discussion

27572.	Find A^(2)-5A+6I, if A=[{:(2,0,1),(2,1,3),(1,-1,0):}].
Answer» ANSWER :`[{:(1,-1,-3),(-1,-1,-10),(-5,4,4):}]`

Discussion

27573.	Show that the function f : R rarr Rgiven by f(x) =x^(3)is injective.
Answer» SOLUTION :N/A

Discussion

27574.	Show that1 + 1/2.3/5 + (1.3)/(2.4) (3/5)^2 + (1.3.5)/(2.4.6) (3/5)^3 + …… = sqrt([5/2])
Answer» ANSWER :`SQRT(5/2)`

Discussion

27575.	Find A^(2)-5A+6I, if A=[(2,0,1),(2,1,3),(1,-1,0)]
Answer» ANSWER :`[(1,-1,-3),(-1,-1,-10),(-5,4,4)]`

Discussion

27576.	The valueofsin^(-1) (cos ((43pi)/5))is :
Answer» `(3PI)/5` `(-7pi)/5` `PI/10` `(-pi)/10` ANSWER :D

Discussion

27577.	Which of the following is a root of the equation x/(x+2)=3/x+4/(x(x+2)) ?
Answer» 5 2 `-2` 0 Answer :A

Discussion

27578.	If A(2, -1), B(3, 1), C(1, -2) then the radical centre of the circles with AB, BC, CA as diameters is
Answer» (1,-2) (2,1) (11,-7) (4,7) Answer :C

Discussion

27579.	Find the area of the circle 4x^(2) + 4y^(2) = 9 which is interior to the parabola x^(2) = 4y.
Answer» ANSWER :`sqrt2/6+9/4 SIN^(-1) ""(2SQRT2)/(3)`

Discussion

27580.	The standard deviation of 15 items is 6 and each item is decreased by 1. Then find the standard deviation of new data.
Answer» ANSWER :6

Discussion

27581.	The mean of the numbers obtained on throwing a die having written 1 on three faces, 2 on two faces and 5 on one face is
Answer» 1 2 5 `(8)/(3)` ANSWER :B

Discussion

27582.	Find an anti derivative (or integral) of the following functions by the method of inspection. sin 2x – 4 e^(3x)
Answer» ANSWER :`-1/2cos2x-4/3e^(3X)`

Discussion

27583.	If A, B, C, be the centres of three co-axial circles and t_(1),t_(2),t_(3) be the lengths of the tangents of them any piont, prove that bar(BC).t_(1)^(2)+bar(CA).t_(2)^(2)+bar(AB).t_(3)^(2)=0
Answer» ANSWER :which PROVES the RESULT.

Discussion

27584.	int _0 ^(pi)( xdx) /( 4cos^2x + 9 sin ^2 x)=
Answer» `(pi^2)/(12)` `(pi^2)/(4)` `(pi^2)/(6)` `(pi^2)/(3)` ANSWER :A

Discussion

27585.	If the demand function is p=200-4x, where x is the number of units demand and p is theprice per unit, the marginal revenue is
Answer» `200-10x` `200+8x` `200-8x` `200+10x` SOLUTION :N/A

Discussion

27586.	intcot^4thetacosec^4theta d theta
Answer» Solution :`intcot^4thetacosec^4theta d theta` `intcot^4theta(1+cot^2theta).cosec^4theta d theta` [Put `cottheta=t` Then`cosec^2thetad theta=-DT` = `intt^4.(1+t^2).(-dt)=-INT(t^4+t^6)dt` =`-{1/5t^5+1/7t^7}+C` =`-{1/5cot^5theta+1/7cot^7theta}+C` =`-1/5cot^5theta-1/7cot^7theta+C`

Discussion

27587.	Find the equation of the circle passing through (2,-3) , (-4,5) and having the centre on4x+ 3y+1=0 .
Answer» ANSWER :`x^(2) +y^(2) +2X -2Y -23 =0 `

Discussion

27588.	The term independent of x in the expansion of (1+x+2x^3) (3x^2//2-1//3x)^9 is
Answer» SOLUTION :N/A

Discussion

27589.	An insurance company insured 2000 scooter drivers, 4000 car drivers and 6000 truck drivers. The probability of an accidents are 0.01, 0.03 and 0.15 respectively. One of the insured persons meets with an accident. What is the probability that he is a scooter driver ?
Answer» ANSWER :`(1)/(52)`

Discussion

27590.	If a set of m paralled lines intersect another set of n parallel lines (not parallelto the lines in the first set), then find the number of parallelograms fromed in this lattice structure.
Answer» MN `C(m,2)XXC(n,2)` `C(m,2)+C(n,2)` `C(m+,4)` ANSWER :B

Discussion

27591.	Integration using trigonometric identities : int tan^(4)x dx=....
Answer» `TAN^(3)x-tanx+x+c` `(1)/(3)tan^(3)x-tanx+x+c` `(1)/(3)tan^(3)x+tanx+x+c` `(1)/(3)tan^(3)x+tanx+x+c` ANSWER :B

Discussion

27592.	Integrate the functions (1)/(sqrt(sin^(3)xsin(x+alpha)))
Answer» Answer :`(-2)/(SINALPHA)SQRT((sin(x+alpha))/(sinx))+C`

Discussion

27593.	if thetangentat theends B and B'of minoraxisatL and L'respectively , thenB:.B'.L'=
Answer» `a^(2)` `B^(2)` `a^(2)+b^(2)` `A^(2)=b^(2)` ANSWER :A

Discussion

27594.	Let X = {1,2,3,4,5,6,7,8,9}. Let R _(1) be a relation in X given by R_(1) = {(x,y): {x,y} sub {1,4,7}} or {x,y} sub {2,5,8} or {x,y} sub {3,6,9}}. Show that R _(1) = R _(2).
Answer» ANSWER :`R _(2) SUB R _(1)`

Discussion

27595.	Solve : x^6-6x^5+13x^4-12x^3+7x^2-6x-5=0if (1+sqrt2) and (2+i) are roots.
Answer» ANSWER :`1+sqrt2,1-sqrt2,2+I,2-I,i-i`

Discussion

27596.	If the coefficients of r,(r +1 ),(r+2) terms in (1+x)^14 are in A.P. then r =
Answer» 3,2 5,9 2,4 5,3 Answer :B

Discussion

27597.	A vector has magnitude 5 units. It is parallel to the resultant vectors of vec(a)=2hati+3hatj-hatk and vec(b)=hati-2hatj+hatk. Find this vector.
Answer» Answer :`(3)/(2)SQRT(10)hati+(sqrt(10))/(2)HATJ`

Discussion

27598.	A boat's crew consists of 8 men, 3 of whom can only row on one side, 2 only on the other. The number ofwaysthe crew can be arranged.
Answer» 1728 `14 XX 9 !` `""^(12)C_(8)` `""^(9)C_(5)` Answer :A

Discussion

27599.	Find the Cartesian equation of the following planes :(a) vecr.(hati+hatj-hatk)=2(b) vecr.(2hati+3hatj-4hatk)=1(c) vecr.((s-2t)hati+(3-t)hatj+(2s+t)hatk)=15
Answer» ANSWER :(a) `THEREFORE X+y-z=2` (B) `therefore 2x+3y-4z=1` (C) `therefore(s-2t)x+(3-t)y+(2s+t)z=15`

Discussion

27600.	If A=[{:(1,2,-1),(-1,1,2),(2,-1,1):}] then det(ad(adjA))=….
Answer» `(14)^2` `(14)^3` `(14)^4` `(10)^1` Answer :C

Discussion

Explore topic-wise InterviewSolutions in .

Write{1,3,9,27)set in the intention(or specification form).

Evalute: int((1+logx)^2)/(x)dx

Using elementary transformations, find the inverseof the matrices [(2,1),(1,1)]

Find the derivative (dy)/(dx)of functions represented parametrically : (a)x = int_(2)^(1) (I n z)/( z) dz, y = int_(5)^(I n t) e^(z) dz (b)x = int_(c^(2))^(sin t) " arc sin z dz, " y = int _(n)^(sqrt(t)) (sin z^())/(z) dz

There are 100 stations between two stations A and B. A train is to stop at ten of these 100 stations. What is the probability that no two of these ten stations are consecutive.

Ifveca=hati+hatj+hatk,vecb=hati+hatj, vecc= veciand(vecaxxvecb))xxvecc=lambdaveca+muvecbthen the value oflambda + muis._______

If f2f(x) +3f (-x) =x^(2) -x+1, then the value of f'(1) is-

Find the area bounded by curves (x - 1)^(2) + y^(2) = 1" and "x^(2) + y^(2) = 1.

If x_(1), x_(2), x_(3), x_(4) are positive roots of the equation x^(4)-8x^(3)+ax^(2)-bx+16=0 then tan^(-1)(x_(1))+tan^(-1)(x_(2))+tna^(-1)(x_(3))+tan^(-1)(x_(4)) can be equal to

Solve the inequation |a^(2x)+a^(x+2)-1|ge1 for all values of a(agt0,a!=1)

Differentiate the functions given in Exercises 1 to 11 w.r.t. x. 2^(sin x).

A man of height 2 metres walks at a uniform speed of 5 km/h away from a lamp post which is 6 metres high. Find the rate at which the length of his shadow increases.

int(sinx + cos x) dx

If 7x-2lt 4 - 3x and 3x-1 lt 2 + 5x, then x lies in the interval

f(x) is a strictly increasing function, iff'(x) is........a)Positive b)Negative c)0 d)None of these

BagI contains 3 red and 4 black balls while another Bag II contains 5 red and 6 black balls. One ball is drawn at random from one ofthe bags and it is found to be red. Find the probability that it was drawn from Bag II.

A point (x,y,z) moves parallel to xy-plane. Which of the three variables x,y,z remains fixed? (A) x and y (B) y and z (C) z and x (D) none of these

Let y be an implicit functio of x defined by x ^(2x) - 2x ^(x) cot y-1 =0. Then y'(1) equals

Find A^(2)-5A+6I, if A=[{:(2,0,1),(2,1,3),(1,-1,0):}].

Show that the function f : R rarr Rgiven by f(x) =x^(3)is injective.

Show that1 + 1/2.3/5 + (1.3)/(2.4) (3/5)^2 + (1.3.5)/(2.4.6) (3/5)^3 + …… = sqrt([5/2])

Find A^(2)-5A+6I, if A=[(2,0,1),(2,1,3),(1,-1,0)]

The valueofsin^(-1) (cos ((43pi)/5))is :

Which of the following is a root of the equation x/(x+2)=3/x+4/(x(x+2)) ?

If A(2, -1), B(3, 1), C(1, -2) then the radical centre of the circles with AB, BC, CA as diameters is

Find the area of the circle 4x^(2) + 4y^(2) = 9 which is interior to the parabola x^(2) = 4y.

The standard deviation of 15 items is 6 and each item is decreased by 1. Then find the standard deviation of new data.

The mean of the numbers obtained on throwing a die having written 1 on three faces, 2 on two faces and 5 on one face is

Find an anti derivative (or integral) of the following functions by the method of inspection. sin 2x – 4 e^(3x)

If A, B, C, be the centres of three co-axial circles and t_(1),t_(2),t_(3) be the lengths of the tangents of them any piont, prove that bar(BC).t_(1)^(2)+bar(CA).t_(2)^(2)+bar(AB).t_(3)^(2)=0

int _0 ^(pi)( xdx) /( 4cos^2x + 9 sin ^2 x)=

If the demand function is p=200-4x, where x is the number of units demand and p is theprice per unit, the marginal revenue is

intcot^4thetacosec^4theta d theta

Find the equation of the circle passing through (2,-3) , (-4,5) and having the centre on4x+ 3y+1=0 .

The term independent of x in the expansion of (1+x+2x^3) (3x^2//2-1//3x)^9 is

An insurance company insured 2000 scooter drivers, 4000 car drivers and 6000 truck drivers. The probability of an accidents are 0.01, 0.03 and 0.15 respectively. One of the insured persons meets with an accident. What is the probability that he is a scooter driver ?

If a set of m paralled lines intersect another set of n parallel lines (not parallelto the lines in the first set), then find the number of parallelograms fromed in this lattice structure.

Integration using trigonometric identities : int tan^(4)x dx=....

Integrate the functions (1)/(sqrt(sin^(3)xsin(x+alpha)))

if thetangentat theends B and B'of minoraxisatL and L'respectively , thenB:.B'.L'=

Let X = {1,2,3,4,5,6,7,8,9}. Let R _(1) be a relation in X given by R_(1) = {(x,y): {x,y} sub {1,4,7}} or {x,y} sub {2,5,8} or {x,y} sub {3,6,9}}. Show that R _(1) = R _(2).

Solve : x^6-6x^5+13x^4-12x^3+7x^2-6x-5=0if (1+sqrt2) and (2+i) are roots.

If the coefficients of r,(r +1 ),(r+2) terms in (1+x)^14 are in A.P. then r =

A vector has magnitude 5 units. It is parallel to the resultant vectors of vec(a)=2hati+3hatj-hatk and vec(b)=hati-2hatj+hatk. Find this vector.

A boat's crew consists of 8 men, 3 of whom can only row on one side, 2 only on the other. The number ofwaysthe crew can be arranged.

Find the Cartesian equation of the following planes :(a) vecr.(hati+hatj-hatk)=2(b) vecr.(2hati+3hatj-4hatk)=1(c) vecr.((s-2t)hati+(3-t)hatj+(2s+t)hatk)=15

If A=[{:(1,2,-1),(-1,1,2),(2,-1,1):}] then det(ad(adjA))=….