Explore topic-wise InterviewSolutions in .

This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.

351.

If A=[(sinalpha,-sinalpha),(sinalpha,cosalpha)], then A+A'=I, if the value of alpha is :

Answer»

`PI/6`
`pi/3`
`pi`
`(3PI)/(2)`.

ANSWER :B
Discussion
352.

The radius of a sphere decreases from 10 cm to 9.9 cm. Find (i) approximate decrease in its volume. (ii) approximate decrease in its surface.

Answer»


ANSWER :`(i) 40 pi CM^(3)(ii) 8 pi cm^(2)`
Discussion
353.

If |z- 25i| le 15 , then |maximum arg (z) - minimum arg (z)| equals

Answer»

`2 Cos^(-1) (3//5)`
`2 Cos^(-1) (4//5)`
`(PI)/(2) + Cos^(-1) (3//5)`
`SIN^(-1) (3//5) - Cos^(-1) (3//5)`

Answer :B
Discussion
354.

A cylindrical .................

Answer»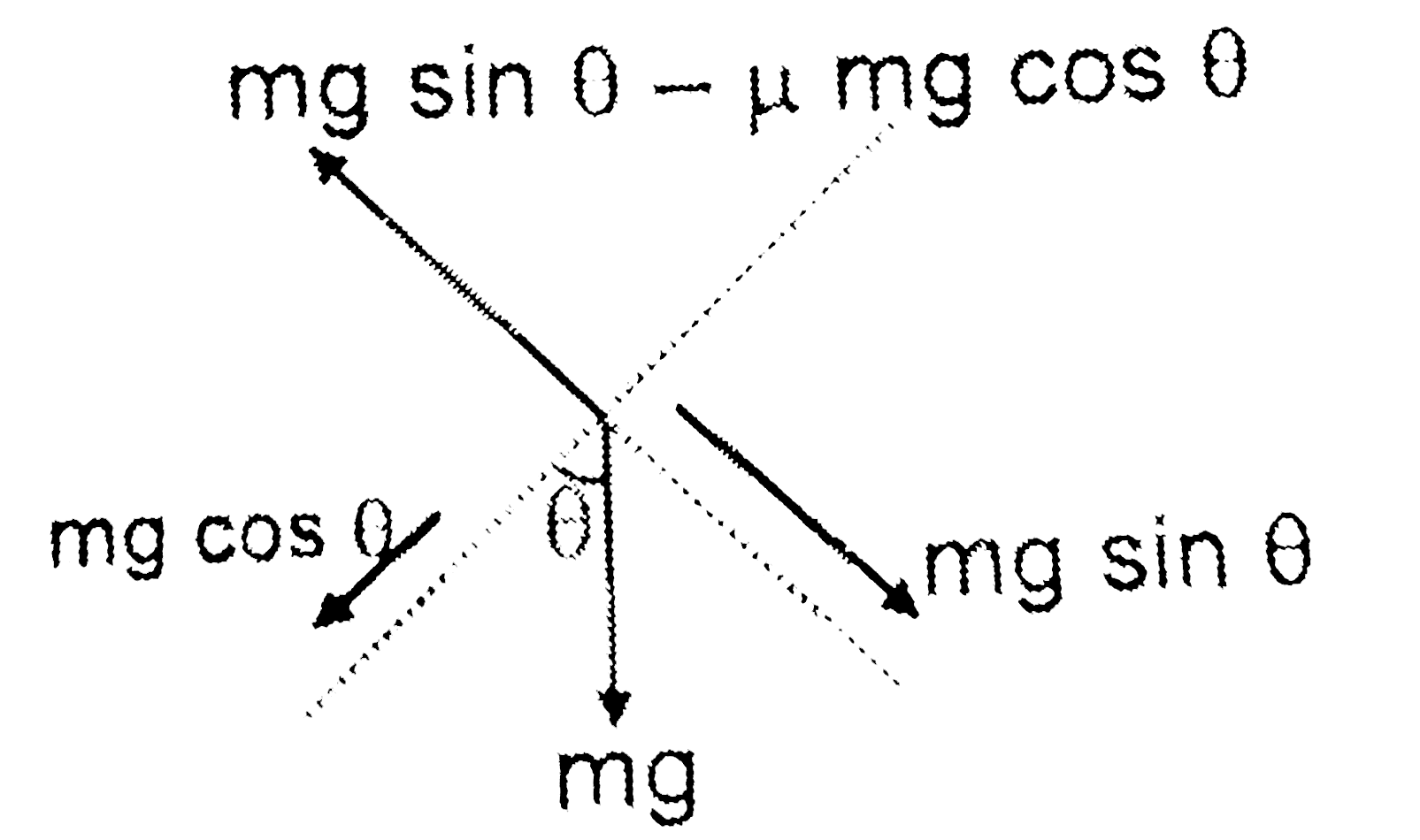


Solution :Figure below shows FORCES acting on a 'particle' on the surface with respect to VESSEL

`mg sin THETA - mu mg cos theta` is pseudo FORCE
Here if `phi` is angle made by water surface with incline, we use
`tan phi =(mu mg cos theta)/(mg cos theta)=mu`
`phi` is angle between normal to the inclined surface and the resultant force. the same angle will be formed between the surface of water & the inclined surface.
Discussion
355.

There are 6 white and 4 black balls in a bag. If four are drawn successively (and not replaced),find the probability that they are alternately of different colour.

Answer»

SOLUTION :There are 6 white and 4 black balls in a bag. Four balls are DRAWN without replacement. Let W and B denotes the white and black ball. There are TWO mutually exclusive cases WBWB and BWBW.
`therefore P(WBWB)=6/10xx4/9xx5/8xx3/7=1/14`
P(BWBW)=`4/10xx6/9xx3/8xx5/7xx=1/14`
`therefore` Probability that they are ALTERNATELY of different colour`=1/14+1/14=2/14=1/7`
Discussion
356.

An ordered triplet solution (x,y,z) with x,y,z int (0,1) and satisfying x^(2)+y^(2)+z^(2) + 2xyz=1 is

Answer»

`(cospi/6, cos (7pi)/18, cos(4PI)/9)`
`(cos (2pi)/5, cos(PI)/3, cos pi/10)`
`(cos (7pi)/12, cospi/4, cos pi/6)`
`(cos pi/12, cos (4pi)/9, cos (17pi)/36)`

Answer :A::D
Discussion
357.

If the marginal revenue (MR) function is defined as the rate of change of total revenue (R ) with respect to the quantity demanded at an instant. IF the marginal revenue of a function is given by: MR=25 e^(-x//400) (1-x/100) find the total revenue function through integration, putting the condition that R=6 when x=0

Answer»


ANSWER :`R=25`
Discussion
358.

For all real values of x, the minimum value of f(x)=(1-x+x^(2))/(1+x+x^(2)), AA x in R is ……….

Answer»

0
1
3
`(1)/(3)`

ANSWER :D
Discussion
359.

Arandom variable x takes the values 0, 1, 2, 3 and its mean is 1.3. If P(x=3)=2 P(x=1) and P(x=2)=0.3, then P(x=0)=

Answer»

0.1
0.2
0.3
0.4

Answer :D
Discussion
360.

If veca.vecb=0 then angle between vector veca and vecb is:

Answer»

pi/2
pi/6
pi/4
pi/3

Answer :A
Discussion
361.

Removesecondterm( secondhigherpowerof x )fromthe equation x^3 +6x^2 + 4x +4=0

Answer»


ANSWER :`x^3 -8X +12=0`
Discussion
362.

A letter is known to have come either from word TATA NAGAR or from CALCUTTA, On the envelope, just two consecutive letter TA are visible. What is the probability that the letter came from TATA NAGAR ?

Answer»


ANSWER :`(7)/(11)`
Discussion
363.

Bohr effect is :-

Answer»

The EFFECT of `Co_(2)` on haemoglobin
The effect of `CO_(2)` on oxyhaemoglobin
The effect of `CO_(2)` on RBC
The effect of `O_(2)` on haemoglobin

Answer :A
Discussion
364.

int sqrt(1+x^(2))dx=....

Answer»

`(X)/(2)sqrt(1+x^(2))+(1)/(2)log|(x+sqrt(1+x^(2)))|+C`
`(2)/(3)(1+x^(2))^((3)/(2))+c`
`(2)/(3)x(1+x^(2))^((3)/(2))+c`
`(x^(2))/(2) sqrt(1+x^(2))+(1)/(2)x^(2) log|x+ sqrt(1+x^(2))|+c`

Answer :A
Discussion
365.

Using elementary row transformations , find the inverse of [{:(6,-3),(-2,1):}]

Answer»


Answer :`=[{:(1,-3),(0,1):}]A"" R_(1)toR_(1)-3R_(2)`
Discussion
366.

STATEMENT-1 : Ifa^(x) = b^(y) = c^(z) ,where x,y,z are unequal positive numbers and a, b,c are in G.P. , thenx^(3) + z^(3) gt 2y^(3)and STATEMENT-2 :If a, b,c are in H,P,a^(3) + c^(3) ge 2b^(3) , where a, b, c are positive real numbers .

Answer»

Statemant-1 is True , Statement-2 is True, Statement -2 is a CORRECT explanation for Statement-1
Statemant-1 is True , Statement-2 is True, Statement -2 is NOTa correct explanation for Statement-1
Statement-1 is True, Stetement-2 is FALSE.
Statement-1 is False, Statement-2 is True

Answer :1
Discussion
367.

The radius of the circle given by x^(2)+y^(2)+z^(2)+2x-2y-4z-19=x+2y+2z+7, is

Answer»

4
3
2
1

Answer :B
Discussion
368.

If A=[{:(1,0," 0"),(3, 3," 0"),(5,2,-1):}] then, adj A is

Answer»

`[{:(-3,"0","0"),("3", -1,"0"),(-9,"2",-3):}]`
`[{:(0, 0,"-3"),(0, "-1",3),(3,"-2","-9"):}]`
`[{:(3, 0,0),("-3", "-1",0),(9,2,"-3"):}]`
`[{:(0, 0,3),(0, 1,"-3"),("-3",2,9):}]`

ANSWER :A
Discussion
369.

(i) One kind of cake requires 200 g of flour and 25 g of fat and another kind of cake requires 100 g of flour and 50 g of fat.Find the maximum number of cakes which can be made form 5 kg of flour and 1 kg of fat assuming that there is no shortage of the other ingredients used in making the cakes.From a linear programming problem and solve it graphically. (ii) One kind of cake requires 300 g of flour and 15 g of fat, another kind of cake requires 150 g of flour and 30 g of fat.Find the maximum number of cakes which can be made from 7.5 kg of flour and 600 g of fat assuming that there is no shortage of the other ingredients used in making the cakes. Make it as an LPP and solve it graphically.

Answer»


ANSWER :(i) -(II)Max. Number of CAKES = 30, 20 cakes of KIND one and 10 cakes of another kind.
Discussion
370.

Consider a family of circles passing through the point (3,7) and (6,5). Answer the following questions. If the circle which belongs to the given family cuts the circle x^(2)+y^(20=29 orthogonally, then the center of that circle is

Answer»

`(1//2,3//2)`
`(9//2,7//2)`
`(7//2,9//2)`
`(3,-7//9)`

Solution :The equation of the line passing through the points A(3,7)and B(6,5) is
`y-7= - (2)/(3) (x-3)`
or `2x+3y -27 =0`
Also, the equation of the circle with A and B as the endpoints of DIAMETER is
`(x-3) (x-6) +(y-7) (y-5) =0`
Now, the equation of the family of circles through A and B is
`(x-3)(x-6)+(y-7)(y-5)+lambda(2x+3y-27)=0`(1)
If the circle BELONGING to this family touches the x-axis , then equation `(x-3)(x-6)+(0-7)(-5)+lambda { 2x+3(0)-27}=0` has two equal roots, for which discriminanat `D=0`. It gives two values of `lambda`.
The equation of the common chord of (1) and `x^(2)+y^(2)-4x-6y-3=0` is the radical axis,which is
`[(x-3)(x-6)+(y-7)(y-5)+lambda(2x+3y-27)] -[x^(2)+y^(2)-4x-6y-3]=0`
or `(2 lambda -5)x+(3 lambda -6)y +(-27 lambda + 56) = 0`
or `(-5x-6y+56)+lambda(2x+3y-27)=0`
This is the family of lines which passes through the point of intersection of `-5x-6y+56=0` and `2x+3y-27=0, i.e., (2,23//3)`.
If circle `(i)` CUTS `x^(2)+y^(2)=29` orthogonally , then
`0+0= -29 +56-27 lambda =0` or `LAMDA =1`
So, the required circle is `x^(2)+y^(2)-7x-9y+26=0` and the center is `(7//2,9//2)`.
Discussion
371.

If p,q are the roots of ax^(2)-25x+c=0, then p^(3)q^(3)+p^(2)q^(3)+p^(3)q^(2)=

Answer»

`(C^(2)(c+25))/(a^3)`
`(c^(3)(c-25))/(a^3)`
`(bc^3)/(a^3)`
`(bc^2)/(a^2)`

ANSWER :A
Discussion
372.

Prove that |{:((1+ax)^(2),(1+ay)^(2),(a+az)^(2)),((1+bx)^(2),(1+by)^(2),(1+bz)^(2)),((1+cx)^(2),(1+cy)^(2),(1+cz)^(2)):}|=2(a-b)(b-c)(c-a)(x-y)(y-z)(z-x).

Answer»

`(a-b)(b-c)(c-a)`
`(x-y)(y-z)(z-x)(a-b)(b-c)(c-a)`
`(x-y)(y-z)(z-x)`
`2(a-b)(b-c)(c-a)(x-h)(y-z)(z-x)`

ANSWER :D
Discussion
373.

I : int (1)/( cos x sin^(2) x)dx= log |tan (x)/(2)|+sec x+c II int (1)/(cos x+ sin^(2)x)dx= "cosec" x+ log |sec x + tan x|+c

Answer»

only I is TRUE
only II is true
both I and II are true
NEITHER I nor II true

Answer :1
Discussion
374.

A G.P. consist of 2n terms. If the sum of the terms occupying the odd places is S, and that of the terms occupying the even places is S_(2)then find the common ratio of the progression.

Answer»


ANSWER :`(S_(2))/(S _(1))`
Discussion
375.

The number of ways in which an examiner can assign 30 marks to 8 questions given not less than 2 marks to any question is

Answer»

`""^(21)C_(7)`
`""^(20)C_(7)`
`""^(30)C_(8)`
1412

Answer :A
Discussion
376.

How many different four letter words can be formed by using the four letters a,b, c, d, while the letter can be repeated ?

Answer»

Solution :The number of different words that can be FORMED by USING the FOUR letters a,B,c,d, while the letter can be REPEATED is `4^4=256.`
Discussion
377.

A hyperbola whose transverse axis is along the major of the conic, (x^2)/3+(y^2)/4=4 and has vertices at the foci of this conic. If the eccentricity of the hyperbola is 3/2, then which of the following points does NOT lie on it?

Answer»

`(sqrt5, 2SQRT2)`
(0,2)
`(5,2SQRT3)`
`(sqrt10, 2sqrt3)`

ANSWER :C
Discussion
378.

Evalute the following integrals int (dx)/(1 + e^(x))

Answer»


ANSWER :`X-log(1+e^(x))+C`
Discussion
379.

If the direction cosines of a line are k,k,k , then

Answer»

K GT 0
0 lt k lt 1
k=1
`k=1/3` or `(-1)/SQRT3`

ANSWER :D
Discussion
380.

Which of the following graphs is the graph of function g(x)|x-1|-1?

Answer»




ANSWER :C
Discussion
381.

If f: R rarr R is defined by f(x)=(x)/(x^(2)+1) find f(f(2))

Answer»

1)29
2)`(29)/(10)`
3)`(10)/(29)`
4)`(1)/(29)`

Answer :C
Discussion
382.

Consider a family of cirlces which are passing through the point (-1,1) andthe tangents to x- axis. If (h,k) is the centre of circle, then show that Kge1/2.

Answer»


ANSWER :`Kge1/2`
Discussion
383.

Joint equation of the two lines x+y=1 and x-y=4 is

Answer»

`X^(2)-y^(2)=-4`
`x^(2)-y^(2)=4`
`(x+y-1)(x-y-4)=0`
`(x+y+1)(x-y+4)=0`

ANSWER :C
Discussion
384.

If 3 dice are rolled, find the probability that either sum is 16 or they show different numbers.

Answer»


ANSWER :`(7)/(12)`
Discussion
385.

Assertion (A) : thesumand product of the slopes of the tangents to the ellipse (x^2)/(9)+(y^2)/(4)=1 drawn from the points (6,-2) are -8/9,1.Reason(R): if m_(1),m_(2)are the slopes of the tangents through(x_(1),y_(1))of the ellipse, then m_(1)+m_(2)=(2x_(1).y_(1))/(x_(1)^(2)-a^(2))m_(1).m_(2)=(y_(1)^(2)-b^(2))/(x_(1)^(2)-a^(2))

Answer»

A TRUE, R true & R is CORRECT exp. of A
A true, R true & R is not correct explanation of A
A true, R false
A false, R true

Answer :D
Discussion
386.

Assertion (A) : A question paper contains 5 questions each having an alternative. The number of ways that an examinee can answer one or more questions is 242. Reason (R): The number of ways of answering one or more of n questions when each question have an alternative is 3^(n)-1. The correct answer is

Answer»

Both A and R are TRUE and R is the CORRECT explanation of A
Both A and R are true but R is not correct explanation of A
A is true but R is false
A is false but R is true

ANSWER :A
Discussion
387.

Let three positive numbers a, b c are in geometric progression, such that a, b+8, c are in arithmetic progression and a, b+8, c+64 are in geometric progression. If the arithmetic mean of a, b, c is k, then (3)/(13)k is equal to

Answer»


ANSWER :4
Discussion
388.

The mean of a set of 30 observations is 75. If each observations is multiplied by a non-zero numberse lambda and then each observations is decreased by 25, their mean remains the same. Thenlambdais equal to

Answer»

`( 1)/(3)`
` ( 2)/(3)`
` ( 4)/(3)`
` ( 10 )/(3)`

Answer :C
Discussion
389.

Find the value of a,b,c,x,y and z. [{:(x+3,z+4,2y-7),(4x+6,a-1,0),(b-3,3b,z+ac):}]=[{:(0,6,3y+2),(2x,-3,2c+2),(2b+4,-21,0):}]

Answer»


ANSWER :`a=-2,b=-7,c=-1,x=-3,y=-5,z=-2`
Discussion
390.

int_(0)^(pi//2) (3 Sec x + 5 cosec x)/(Sec x + cosec x) dx=

Answer»

`PI`
`4PI`
`6PI`
`2PI`

ANSWER :D
Discussion
391.

R is a relation from {11, 12, 13} to {8, 10, 12} defined by y=x-3. Then R^(-1) is

Answer»

`{(8,11),(10,13)}`
`{(11,8),(13,10)}`
`{(10,13),(8,10)}`
`{(11,8),(10,13),(12,15)}`

ANSWER :A
Discussion
392.

Find the value of a if,lim_(xto0)(tanax)/(sin2x)=1

Answer»

Solution :`lim_(xto0)(tanax)/(sin2x)=1`
`implieslim_(xto0)((tanax)/(ax)XXA)/((sin2x)/(2X)xx2)=1`
`a/2=1impliesa=2`
Discussion
393.

If A (1,2,3), B (2,3,1), C (3,1,2) then the length of the altitude through C is

Answer»

3
`3 SQRT(3)`
`3 sqrt(2)`
`3// sqrt(2)`

ANSWER :D
Discussion
394.

Find the coefficient of x^15 in the expansion of (2x^12 - (3)/(x^3) )^5

Answer»


ANSWER :`-1080`
Discussion
395.

Let AX=B where A is 3 xx 3 and X and B are 3 xx 1 matrices then which of the following is correct?

Answer»

If |A|=0 then AX=B has INFINITE solutions
If AX=B has infinite solutions then |A|=0
If (ADJ (A))B=0 `|A|ne0` then AX=B has unique solutions
If (adj (A))BNE0 `|A|ne0` then AX=B has no solution

Answer :B::C::D
Discussion
396.

The tangents at (5,12) and (12,-5) to the circle x^(2)+y^(2)=169 are

Answer»

coincident
perpendicular
parallel
at an ANGLE of `45^(@)`

ANSWER :B
Discussion
397.

A tube of uniform cross sectional sectional area 1 cm^(2) is closed at one end with semi permeable membrane. A solution having 6g glucose per 100 ml is placed inside the tube and dipped in pure water at 27^(@)C. When the equilibrium is established, what will be the osmotic pressure, height developed in vertical column (in meters). Density of glucose solution is 1 gm/ml. (Take R =0.08 L atm mol^(-1) k^(-1), density of Hg=13.8 g/cc)

Answer»


ANSWER :`0.2.5`
Discussion
398.

Evaluate int (1)/(4x + 3x -2x^(2)) dx

Answer»


Answer :`(1)/(SQRT(41)) "log" |(sqrt(41) - 3 + 4X)/(sqrt(41)+ 3 - 4x)| + C`
Discussion
399.

If the area of the triangle with vertices (-2, 0) (0, 4) and (0,k) is 4 square units. Find the value of k using determinants.

Answer»


ANSWER :`THEREFORE k=0,8`
Discussion
400.

If a,b,c are in A.P. and if the equations(b - c) x^(2) + (c - a) x + (a - b) = 0"" (1)and 2(c +a) x^(2) + (b+ c) x = 0"" (2) have a common root, then

Answer»

`a^(2), B^(2), C^(2)` are in A.P.
`a^(2), c^(2), b^(2)` are in A.P.
`c^(2), a^(2), b^(2)` are in A.P.
none of these

Answer :B
Discussion