Explore topic-wise InterviewSolutions in .

This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.

251.

For any integer nge1, the number of positive divisors of n is denoted by dựn). Then for a prime p, d(d(d(p^(7)))) is

Answer»

1
2
3
p

Answer :C
Discussion
252.

Semi transverse axis of hyperbola is 5. Tangent at point P and normal to this tangent meet conjugate axis at A and B, respectively. The circle on AB as diameter passes through tow fixed points, the distance between which is 20. Find the eccentricity of hyperbola.

Answer»

Solution :CONSIDER hyperbola `(x^(2))/(a^(2))-(y^(2))/(B^(2))=1`.
Tangent to it at any point `P(a sec theta, b tan theta)` is
`(x)/(a) sec theta-(y)/(b) tan theta=1`
It MEETS y-axis at `A(0,-b cot theta)`.

NORMAL at point P is
`ax cos theta+by cot theta=a^(2)e^(2)`
It meets y-axis at `B(0,(a^(2)e^(2))/(b) tan theta)`
Now, circle with diameter as AB is
`x^(2)+(y+b cot theta)(y-(a^(2)e^(2))/(b)tantheta)=0`
`rArr""x^(2)+y^(2)-(a^(2)e^(2))+(b cot theta-(a^(2)e^(2))/(b)tantheta)y=0`
This circle passes through fixed point `(pm ae,0)`, DISTNACE between which is 2ae.
`2ae=20"(given)"`
`therefore""e=2`
Discussion
253.

Fork gt 0ifk sqrt(-1)is arootof theequationx^4+ 6x^3 - 16x^2 + 24x- 80 =0thenk^2 =

Answer»

2
3
4
6

Answer :C
Discussion
254.

A factory owner purchases two types of machines, A and B, for his factory. The requirements and limitations for the machines are as follows: He has an area of 7600 sq. m available and 72 skilled men who can operate the machines. To find how many machines of each type should he buy to maximize the daily output, formulate this as a L.P.P.

Answer»


Answer :`Z_(max) ` = 50 x +40 y `
SUBJECT to the constraints :` 5x + 6y ge 38 ;3x+ 2y LE 18 and x ge 0, y ge 0 `
Discussion
255.

Findthe principal value of cos^(-1)(-1/2)

Answer»


ANSWER :`=(2PI)/(3)`
Discussion
256.

If xgt0, the least value of n in N such that ((1+i)/(1-i))^(n)=(2)/(pi)sin^(-1)((1+x^(2))/(2x)) is :

Answer»

2
4
8
32

Solution :`(1+x^(2))/(2) GE x""(because A.M ge G.M.)`
`THEREFORE((E^(i(pi)/(4)))/e^(-i(pi)/(4)))^(N)=(2)/(pi).sin^(-1)(1)`
Discussion
257.

The perimeter of a asector is a constant. If its area is to be maximum, the sectorial angle is

Answer»

`pi^c/6`
`pi^c/4`
`4^c`
`2^c`

ANSWER :D
Discussion
258.

Let the curve C : y = x^(6) + 8x^(5) + bx^(4) + cx^(3) + dx^(2) + ex + f touches the line : y = mx + n at x = 1,2,3. find the area bounded by the these graphs?

Answer»

`(3)/(34)`
`(16)/(105)`
`(5)/(34)`
NONE of these

Answer :B
Discussion
259.

Prove that the relation R in the set of integers z defined by R = { ( x , y) : x-y is an integer } is an equivalence relation.

Answer»


Answer :`RARR ( x, z) in R THEREFORE` R is a transitive relation
Discussion
260.

Let f(n)=sum_(k=-n)^(n)(cot^(-1)((1)/(k))-tan^(-1)(k)) such that sum_(n=2)^(10)(f(n)+f(n-1))=a pi then find the value of (a+1).

Answer»


ANSWER :100
Discussion
261.

Match the following

Answer»

a,B,c,d
c,d,b,a
c,b,d,a
b,a,d,c

Answer :C
Discussion
262.

int (1)/((x^(2)- 25)^(3//2))dx =

Answer»

`(1)/(25).(1)/(SQRT(x^(2)-25)) +C`
`-(1)/(25).(x)/(sqrt(x^(2)-25)) + C `
`(1)/(25).(1)/(sqrt(x^(2)-25)) +C `
`-(1)/(25).(1)/(sqrt(x^(2)-25)) +C `

ANSWER :B
Discussion
263.

Assertion (A) : The Remainder obtained when the polynomial x^(64)+x^(27)+1 is divided by x+1 is 1 Reason (R) : If f(x) is divided by x-a then the remainder is f(a)

Answer»

Both A & R are TRUE and R is correct EXPLANATION of A
Both A & R are true and R is not correct explanation of A
A is true but R is false
A is false but R is true

Answer :A
Discussion
264.

Match the following

Answer»

a,B,C
c,a,b
b,c,a
a,c,b

Answer :B
Discussion
265.

If hati,hatj,hatk are unit vectors along the positive direction of A,Y, and Z- axes, then a FALSE statement in the following is

Answer»

`Sigmahat(i)xx(hatjxxhatk)=vec(0)`
`Sigmahatiuxx(hat(J)+hat(K))=vec(0)`
`Sigmahat(i)*(hat(j)+hat(k))=vec(0)`
`Sigmahati*(hatjxxhat(k))=vec(0)`

Answer :D
Discussion
266.

Find the value of (Sigma_(r=1)^(n) 1/r)/(Sigma_(r=1)^(n) k/((2n-2k+1)(2n-k+1))).

Answer»

SOLUTION :LET
`A=sum_(K=1)^(n)k/((2n-2k+1)(2n-k+1))`
`=sum_(k=1)^(n)((2n-k+1)-(2n-2k+1))/((2n-2k+1)(2n-k+1))`
`sum_(k=1)^(n)1/(2n-2k+1)-sum_(k=1)^(n)1/(2n-k+1)`
`=(1/1+1/3+1/5+..+1/(2n-1))-(1/(n+1)+1/(n+2)+..+1/(2n))`
and `B=sum_(r=1)^(n)1/r=1/1+1/2+1/3+...+1/n+1/(n+1)+1/(n+2)+..+1/(2n))-(1/1+1/3+1/5+..+1/(2n-1))`
`=1/2+1/4+1/6+...1/(2n)`
`=1/2(1/1+1/2+1/3+..+1/n)`
`=B/2`
So, `B-A=1/2B`
`rArrB/2=A`
`rArrB/A=2`
Discussion
267.

If the integral int(cos8x+1)/(cot2x-tan2x)dx=Acos8x+k, where k is an arbitrary constant, then A is equal to

Answer»

`-(1)/(16)`
`(1)/(16)`
`(1)/(8)`
`-(1)/(8)`

ANSWER :1
Discussion
268.

Statement I : In triangleABC, b cos^2(C )/(2)+c cos^2 (B)/(2)=5, Statement II : In triangleABC, cot (A)/(2)=(b+c)/(2) implies /_90^(@) which of the following is correct?

Answer»

Both I and II are TRUE
I is true, II is FALSE
I is false, II is true
Both I and II are false

Answer :B
Discussion
269.

Differentiate w.r.t.x, the following functions : e^(sec^(2)x)+3 cos^(-1)x.

Answer»


Answer :`= 2sec^(2) x TAN XE^(sec^(2)x)+3((1)/(sqrt(1-x^(2))))`.
Discussion
270.

What is the sum of all three digit numbers formed by using the digits 1,2,3,?

Answer»

SOLUTION :The 3 digit numbers that can be formed by using the digits 1,2,3 are :123,132,213,231,312,321.
`:.` Their SUM= 1332.
Discussion
271.

Match column-I and column-II :- {:(,"Duct",,"Organ/Gland"),((A),"Cystic duct",(1),"Pancreas"),((B),"Duct of wirsung",(2),"Liver"),((C),"Hepatic duct",(3),"Gall bladder"),((D),"Stenson's duct",(4),"Salivary gland"):}

Answer»

A (III), B(II), C(iv), D(i)
A (iii), B(i), C(ii), D(iv)
A (ii), B(iii), C(i), D(iv)
A (i), B(ii), C(iii), D(iv)

Answer :A
Discussion
272.

If 1/2x + 1/5y=x+2, what is the value of 2y-5x ?

Answer»

`-10`
`-20`
`-15`
`-25`

ANSWER :B
Discussion
273.

If x and y are digits such that (x^(2)+ax+b)(x^(2)+cx+d)=0thenx + y equals -

Answer»

15
6
12
13

Answer :A
Discussion
274.

A ray of light moving parallel to x-axis gets reflected from a parabolic mirror (y-2)^(2)=4(x+1). After reflection the ray must pass through

Answer»

`(0,2)`
(0,-2)
(2,0)
(1,2)

ANSWER :A
Discussion
275.

Solve log_(x)3log_(x)/(81)3=log_(x)/(729)3

Answer»


ANSWER :B
Discussion
276.

Evaluate the following integrals. int(2x+1)/(x^(2)+x+1)dx

Answer»


ANSWER :LOG(X^(2)+x+1)+C
Discussion
277.

A hunter’s chance of shooting an animal at a distance r is (a^(2))/(r^(2)) (r gt a) . He fires when r =2aif he misses, he reloads and fires again where r = 3a. Further if he misses at r = 3a thenhe tries again at r = 4a. This process continuous till r= na. If he misses at a distance na,the animal escape. Find odd against the event that animal is shot.

Answer»

`N + 1 : 2N `
`n + 1 : n -1 `
`n - 1 : 2n `
`n - 1 : n + 1`

ANSWER :B
Discussion
278.

E_1 , a+b+c=0 if 1isa root ofax ^2 +bx+c=0 . E_2 :b ^2-a^2=2acif sin thetacos thetaare theofax ^2+ bx+c=0 whichof thefollowingis true?

Answer»

`E_1` ISTRUE`E_2` is TRUE
`E_1`istrue`E_2 ` is FALSE
`E_1` is false,` E_2` is TURE
`E_1 ` is false`E_2`is false

ANSWER :A
Discussion
279.

Match the following

Answer»

a,b,c,d
c,d,b,a
c,b,d,a
b,a,d,c

Answer :A
Discussion
280.

Match the following

Answer»

B,C,a,e
b,c,d,e
b,a,c,d
d,c,a,e

Answer :A
Discussion
281.

Match the following

Answer»

b,a,C,d
b,a,d,c
a,b,c,d
b,a,c,E

ANSWER :B
Discussion
282.

If a,b,c are nonzero vectors, then (a xx b) xx c = a (b xx c) iff (a xx c) xx b =

Answer»

a + B
0
a
b

Answer :B
Discussion
283.

IfA+B+C=270^(@) then cos 2A + cos 2B+ cos 2C is equal to

Answer»

`4sin A sin B sin C`
`4 COS A cos B cos C`
`1-4 sin A sin B sin C`
` 1- 5 cos A cos B cos C`

ANSWER :C
Discussion
284.

The probability of an event that person hits the target is (1)/(4). He hits target at least n times. The probability that to hit target n times is more than (2)/(3) thenminimum value of n is ........

Answer»

2
4
6
8

Answer :B
Discussion
285.

Which of the following is not a statement ?

Answer»

Every SET is a finite set
18 is MULTIPLE of 6
Prime numbers are IRRATIONAL numbers
None of these

Answer :D
Discussion
286.

If the direction cosinesof two lines are givenbyl+m+n=0and l^(2)-5m^(2)=0, then the angle between them is

Answer»

`pi/2`
`pi/6`
`pi/4`
`pi/3`

ANSWER :D
Discussion
287.

p(x)=a_(0)+a_(1)x^(2)+a_(2)x^(4)+…………+a_(n)x^(2n) is a polynomial with real variable x. If 0 lt a_(0)lt a_(1)lt a_(2)lt ……….lt a_(n) then p(x) has …………

Answer»

NEITHER MAXIMUM nor minimum
Only ONE minimum
Only one minimum
NONE of these

ANSWER :C
Discussion
288.

Draw the graph of f(x)=[tan^(-1)x]," where "[*]" represents the greatest integer function".

Answer»

Solution :We have `F(x) =[TAN^(-1)x]`
`Now -x//2le tan^(-1) x le pi//2" for x "in R`
`therefore""[tan^(-1)x]=-2,-1,0,1`
`[tan^(-1)x]=-2`
`therefore""-pi//2letn^(-1)xle-1`
`therefore""-oolt-tan1`
`[tan^(-1)x]=-1`
`therefore""-tanletan^(-1)xlt0`
`-tan^(-1)1lexlt0`
`therefore""0letan^(-1)xlt1`
`therefore""0lexlttan1`
`[tan^(-1)x]=1`
`therefore""1letan^(-1)xltpi//2`
`therefore""tan1lexltoo`
So the GRAPH of `f(x) =[tan^(-1)x]` can be drawn as shwon in the FOLLOWING figure.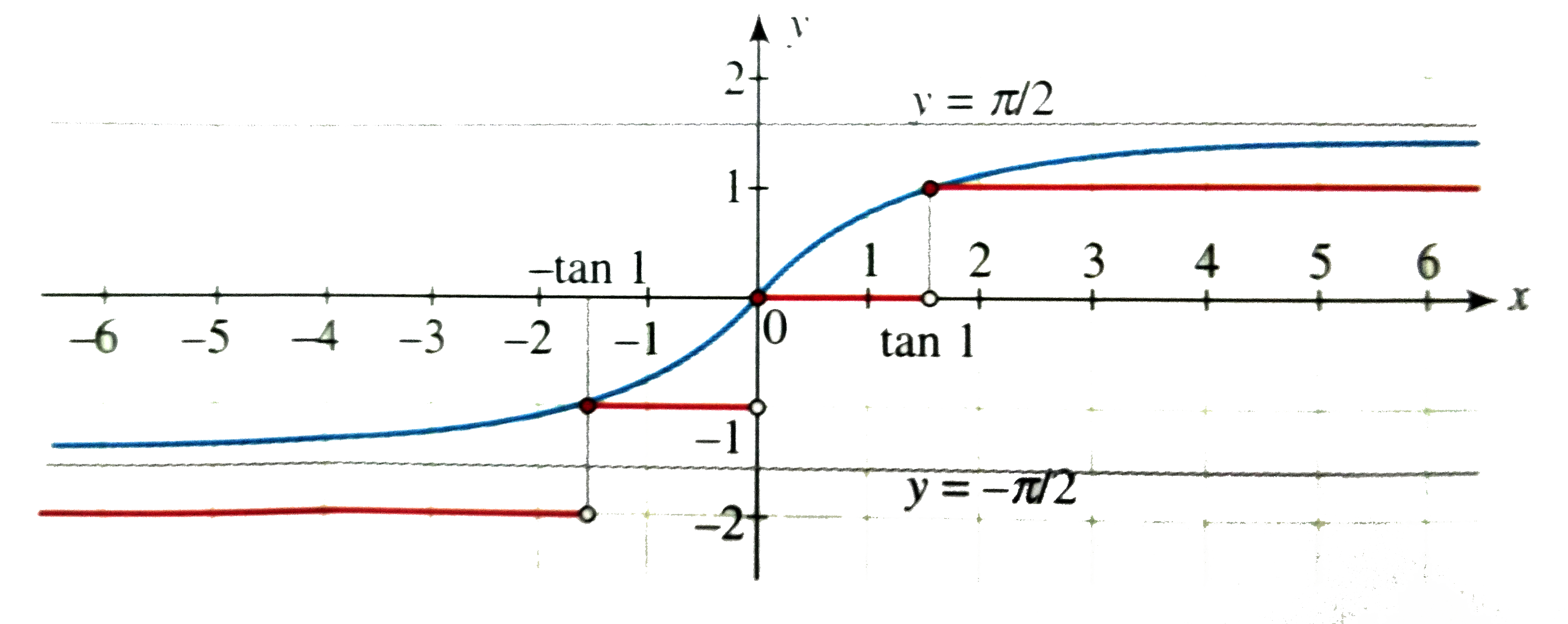
Discussion
289.

Construct the switching circuit for each of the following statements : (1) (p^^q)vv(~p)vv(p^^~q) (2) (p^^q^^r)vv[~pvv(^^~r)] (3) [pvv(~p^^q)]vv[(~q^^r)vv~p]

Answer»

<P>

Solution :Let p : the switch `S_(1)` is closed
q : the switch `S_(2)` is closed
r : the switch `S_(3)` is closed
`~p` : the switch `S_(1)` is closed or the switch `S_(1)` is open
`~q` : the switch `S_(2)'` is closed or the switch `S_(2)` is open
`~r` : the switch `S_(3)'` is closed or the switch `S_(3)` is open.
Then the switching CIRCUITS for the given statements are :
Discussion
290.

The simplified form of(p^^q)vv(p^^r)=

Answer»

`PVV(q^^r)`
`p^^(qvvr)`
`(pvvq)^^r`
NONE of these

Answer :C
Discussion
291.

Write the value of x for which 2tan^(-1)x = cos^(-1)[(1-x^(2))/(1+x^(2))] holds:

Answer»


ANSWER :`X GE 0`
Discussion
292.

Maximum value of (2 cos ^2 18^@ -sin 18^@) (cos theta +3 sqrt2 cos (theta +pi/4)+3) is

Answer»

`5 SQRT2`
`4 SQRT5`
3
8

Answer :D
Discussion
293.

Write the order and degree of the differential equations given by : {y+(dy/dx)^3}^(1//2)=1+x

Answer»

SOLUTION :ORDER = 1, DEGREE = 3
Discussion
294.

underset(n to porp) (lim )(1^(2) +2^(2) ………. +n^(2) (n)^(1//n))/( (n+1) (n+10)(n+10))=

Answer»

`3 `
`(1)/(3)`
`(2)/(3)`
`OO`

ANSWER :D
Discussion
295.

Statement -1 : The minimum value of (x_2-x_1)^2+(sqrt(1+x_1^2)-sqrt(4-x_2^2))^2 =1.because Statement -2 : The expression attains the minimum value if one of the perfect squares vanishes.

Answer»

STATEMENT - 1 is True , Statement -2 is ture , Statement -2 is a correct EXPLANATION for Statement -1
Statement -1 is True , Statement -2 is True , Statement -2 is NOT a correct explanation for statement -1
Statement -1 is True, Statement -2 is False
Statement -1 is False , Statement -2 is True

ANSWER :C
Discussion
296.

Thevalueof kso thatx^4-3x^3 +5x^2 -33 x +kisdivisiblebyx^2 -5x+6is

Answer»

45
48
51
54

Answer :D
Discussion
297.

For …………… value of a, function f(x)=sin x-cos x - ax+b AA x in R is a decreasing function.

Answer»

`a GE - SQRT(2)`
`a LE - sqrt(2)`
`a le sqrt(2)`
`a ge sqrt(2)`

ANSWER :D
Discussion
298.

The range of values of x which satisfy 2x^(2) + 9x + 4 lt 0 and x^(2) - 5x + 6 lt 0 is

Answer»

(-2,-1)
`((1)/(2), 4)`
(2, 3)
`phi`

Answer :D
Discussion
299.

Find distance of (-2, 3, 4) from x-axis is

Answer»

`-2`
5
2
3

Answer :B
Discussion
300.

If A^(3)=I" and "|A|ne0," then "A^(-1)=

Answer»

`-A^(3)`
`A^(3)`
`-A^(2)`
`A^(2)`

ANSWER :D
Discussion