Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 151. |
Show that sin A sin ((pi)/(3)+A) sin ((pi)/(3) -A)=(1)/(4) sin 3A |
|
Answer» |
|
| 152. |
If the matrix A= |{:(1,2,3,0),(2,4,3,2),(3,2,1,3),(6,8,7,alpha):}| is of rank 3, then alpha equals to |
|
Answer» `-5` |
|
| 153. |
C_0 + C_1 + 2.C_2(3) + 3.C_3(3^2)+ 4.C_4(3^3) + ……+n.C_n 3^(n-1) = |
|
Answer» `n.4^(n-1) + 1` |
|
| 154. |
If A ={x:x in I, -2 le x le 2 }, B={x : x in I , 0 le x le 3 }, C={x :x in N , 1 le x le 2}, D={(x,y): (x,y) in N xx N , x+y=8}. Then : |
| Answer» Answer :D | |
| 155. |
If A and B be independent events with P(A) = 1/4 and (P(A cupB) = 2P(B) - P(A), then P(B) is equal to |
|
Answer» `2/5` |
|
| 156. |
L: 3x - 4y = 0 is a diameter of the ellipsex^2/20+y^2/9=1. Y=m'x is the diameter of the ellipse bisecting 20 9 the chords parallel to L. If m represents the slope of L, then the value of (m + m') is equal to |
|
Answer» |
|
| 159. |
Six coins are tossed simultaneously . The odds in favour of getting 2 heads is |
| Answer» Answer :D | |
| 162. |
A tangent to the circle x^(2)+y^(2)=4 meets the coordinate axes at P and Q. The locus of midpoint of PQ is |
|
Answer» `1/(X^(2))+1/(y^(2))=1` |
|
| 163. |
Assertion (A): In theexpansion of (1+x)^n, three consecutive terms are 5, 10,10 then n = 5 Reason (R ): If the coefficient of r^(th), (r + 1)^(th), (r + 2)^(th) terms of (1 +x)^n are in A.P. then (n-2r)^2 = n +2 |
|
Answer» A and R are true , R is CORRECT explanation of A |
|
| 164. |
If real numbers a, b, c, d, e satisfy a+1=b + 2 = c+ 3 = d + 4 = e + 5 = a + b + c + d + e + 3 then find the value of a^2 + b^2 + c^2 + d^2 + e^2 |
|
Answer» |
|
| 165. |
bar(x),bar(y),bar(z) are non zero vectors. If (bar(x)""_(,)^(hat)bar(y))=(pi)/(2 and bar(z)=bar(x)+bar(y), then …….. |
|
Answer» `|BAR(x)|^(2)+|bar(y)|^(2)+|bar(Z)|^(2)=3` |
|
| 167. |
The point ef intersection of the tangents to the circle passing through (4, 7), (5,6) (1,5) at the points where it is cut by the line 5x+y+17=0 |
|
Answer» (-4,2) |
|
| 168. |
If a,P are the eccentric angles of the extremeties of a focal chord of the ellipse (i) e cos (alpha+beta)/(2)=cos (alpha-beta)/(2) (ii) tan (alpha)/(2) tan (beta)/(2)=(e-1)/(e+1) |
|
Answer» |
|
| 169. |
The vector c is perpendicular to both a = (1, -2, -1), b = (2, 1, -1) and c also satisfyies |c xx (I - j + k)| = 2 sqrt(6) then c = |
| Answer» Answer :A | |
| 170. |
Let X be a discrete random variable whose probability distribution is defined as follows: P(X=x)={(k(x+1)",",x="1, 2, 3, 4"),(2kx",",x="5,6,7"),(0"", "Otherwise"):}Where k is a constant. Calculate (i) the value of k (ii) E(X) (iii) Standard deviation of X. |
|
Answer» |
|
| 171. |
Form the differential equations corresponding to the family of curves. (i) y = c(x-2c) where c is a parameter. (ii) y= a cos 3x + b sin 3x where a, b are parameters. (iii) y = a cos x + b sin x where a, b are parameters. (iv) y = a e^(x) + b e^(-x) where a, b are parameters. |
|
Answer» (iii) `y_(2) + y = 0` (iv) `y_(2) = y` |
|
| 172. |
Find the set of all values of a for which the roots of the equation x^2-2ax + a^2 + a-3=0 are less than 3, |
|
Answer» `ALT2` |
|
| 173. |
If f(x)=a+bx+cx^(2)where cgt0 and b^(2)-4aclt0 then the area enclosed by the co-ordinate axes, the line x=2, and the curve y=f(x) is given by |
|
Answer» `(1)/(3){4f(1)+f(2)}` `=(1)/(3)(6a+6b+8c)` `=(1)/(3){f(0)+4f(1)+f(2)}` 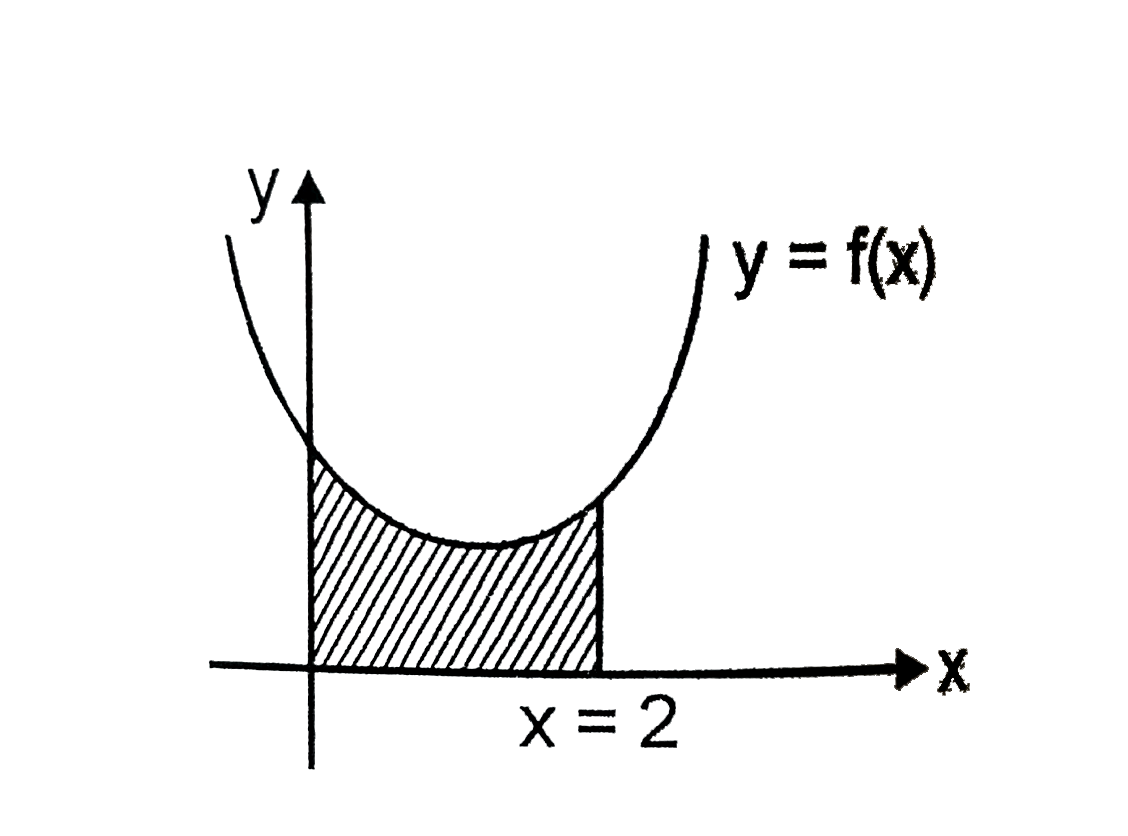
|
|
| 174. |
Evaluate : int_(0)^(pi//2) ( sin x)/(1 +cos^2 x) dx |
|
Answer» |
|
| 175. |
Evaluate the following integrals int(dx)/(1+x^(4)) |
|
Answer» |
|
| 176. |
A: In a Delta ABC, if r_1=2r_2=3r_3 then a:b=5:4. R: In a Delta ABC, if xr_1=yr_2=zr_3=(x+y+z)r then a:b:c=y+z:z+x:x+j |
|
Answer» A is TRUE, R is true and R is CORRECT EXPLANATION of A |
|
| 177. |
If C_1 (1, 3) and C_2(4, 3)are the centres of two circles whose radical axis is y-axis. If the radius of the 1st circle is 2sqrt2 units, then the radius of the second circle is |
|
Answer» `sqrt23` |
|
| 178. |
The symmetric equation of the line passing through (3, 1, - 1) and (3, 2, -6) is …............ |
|
Answer» `(x-3)/(1)=(1-y)/(1)=(z+1)/(5)` |
|
| 180. |
Let f,g:RrarrR be two functions defined as f(x)=|x|+x and g(x)=|x|-xAAx in R. Then f(g) (x) for xlt0 is |
|
Answer» 1)0 |
|
| 182. |
Let P(x) be a polynomial of degree n with leading coefficient 1. Let v (x) be any function and v_(1)(x) = int v (x) dx, v_(2)(x)=intv_(1)(x)dx...v_(n+1)=intv_(n)(x)dx. then int P(x) v(x) dx is equal to |
|
Answer» <P>`P(X)v_(1)(x)+(p'(x)v_(2)(x))/(2!)+(P''(x)v_(3)(x))/(3!)...+(v_(n+1)(x))((n+1)!)`/ |
|
| 183. |
{:("Respiration","Atmosphere","Alveoli","Deoxygenated blood","Oxygenated blood","Tissue"),(O_(2),159,104,B,95,D),(CO_(2),0.3,A,45,C,45):} Correct option for A, B, C, D respectively is :- |
| Answer» Answer :A | |
| 184. |
If B sub C, prove that A\\B =A\\C.Is this result true when difference is replaced by symmetric difference ? Give reason. |
|
Answer» SOLUTION :If `B SUB C`, then `x in B impliesx in C` Now `x in A -C But `A DELTA B != A Delta C` |
|
| 185. |
Consider the frequency distribution If the variance of this distribution is 60000, then the coefficient of variation of the distribution is |
|
Answer» 60 |
|
| 186. |
If ((x-3)^((-|x|)/x) sqrt((x-4)^(2))(17-x))/(sqrt(-x)(-x^(2)+x-1)(|x|-32))lt0 then no. of integers x satisfying the inequality is: |
|
Answer» |
|
| 187. |
underset(n to oo)lim (1.1!+2.2!+3.3!+...+n.n!)/((n+1)!)= |
|
Answer» only I is true |
|
| 188. |
An open topped box is to be constructed by removing equal squares from each corner of a 3 metre by 8 metre rectangular sheet of aluminimum and folding up the sides. Find the volume of the largest such box. |
|
Answer» |
|
| 189. |
The vertices of a triangle ABC are A-=(2,0,2), B(-1,1,1) and C-=(1,-2,4). The points D and E divide the sides AB and CA in the ratio 1:2 respectively. Another point F is taken in space such that the perpendicular drawn from F to the plane containing DeltaABC, meets the plane at the point of intersection of the line segments CD and BE. If the distance of F from plane of triangle ABC issqrt(2), units, ten |
|
Answer» the volume of the tetrahdron `ABCD` is `7/3` CUBIC units `BE:vecr=(-hati+hatj+k)+(mu)/3(7hati-7hatj+7hatk)` `P-=(hati-hatj+3hatj)` Area of tetrahedron `ABCD` `=1/3` (Area of base triangle) `XX` height `=7/3` cubic units `vec(AB)xxvec(AC)=7hatj+7hatk,|vec(PF)|=PF=sqrt(2)` units `vec(PF)=sqrt(2)((7hatj+7hatk)/(sqrt(49+49)))=hatj+hatk=P.V`. of `F-P.V.` of `P` `P.V.` of `F=hati+4hatk` Vector equation of `AF` is `vecr=2(hati+hatk)+ALPHA(-hati+2hatk)` 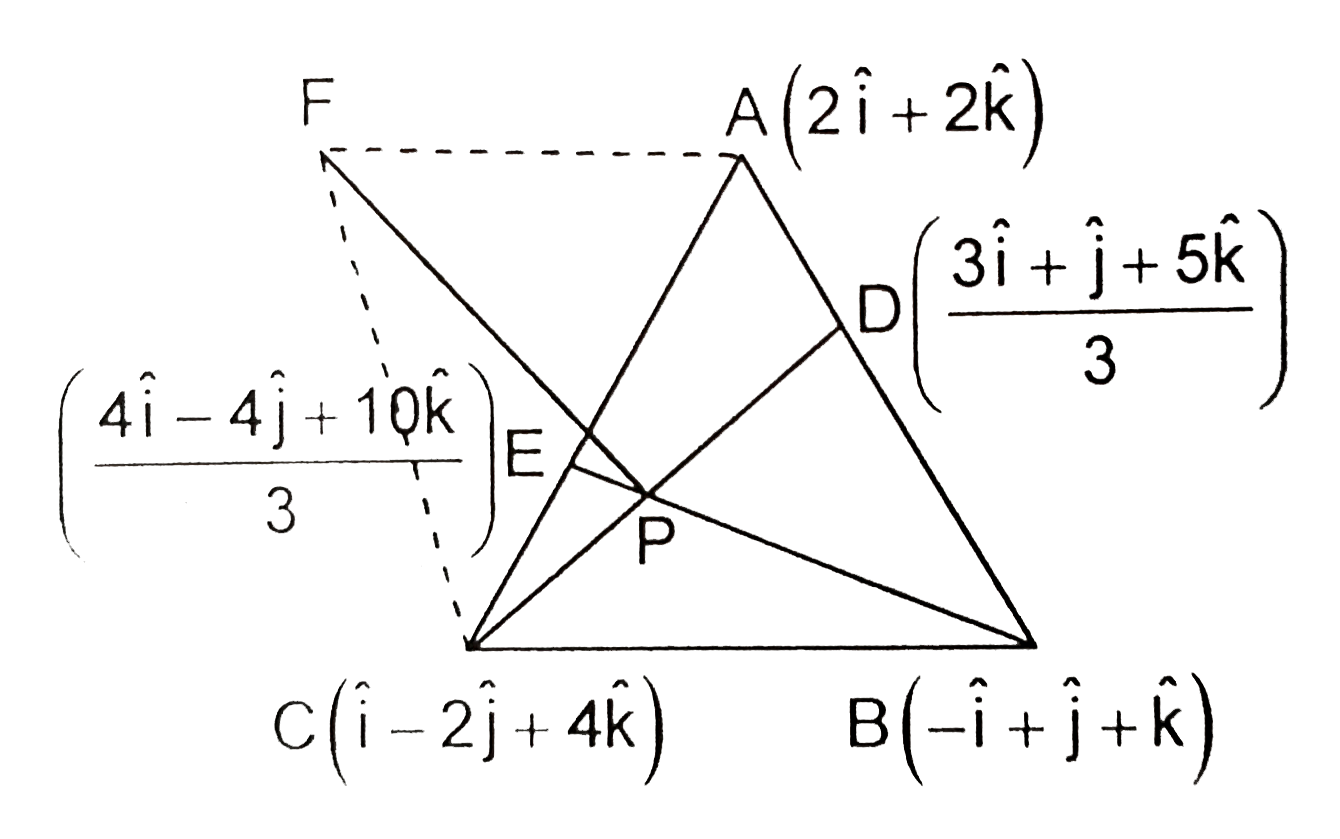
|
|
| 190. |
In the following cases, find the distance of each of the given points from the corresponding given plane.{:("Point","Plane"),("(a) (0, 0, 0)","3x – 4y + 12z = 3"),("(b) (3, -2, 1)","2x - y + 2z + 3 = 0"),("(C) (2, 3, -5)","x + 2y – 2z = 9"),("(d) (6, 0, 0)","2x - 3y + 6z - 2 = 0"):} |
|
Answer» (B) `=(13)/(3)` (C) =3 (d) = 2 |
|
| 191. |
3 numbers are chosen at random from the first 20 natural numbers. Then the probability that the product is even is |
|
Answer» `(.^(10)C_(3))/(.^(20)C_(3))` |
|
| 192. |
f(x) is quadratic expression such that f(x) is negative when x in (-oo, - (5)/(3))cup (3,oo) and positive when x in (- (5)/(3),3) g(x) is another quadratic expression sunc that g (x) is negative when x in (3, 9/4) and positive when x in R - [3,9/2] Then, the sign of f(x) g(x) is [0,5] is |
|
Answer» POSITIVE in `[0,9/2]` and negative in `(9/2, 5)` |
|
| 193. |
If x^(3) + 8xy + y^(3) = 64, then (dy)/(dx) = |
|
Answer» `-(3X^2 + 8Y)/(8X + 3y^2)` |
|
| 194. |
Find the values of x for which y=[x(x-2)]^(2) is an increasing function. |
|
Answer» |
|
| 195. |
Find the differential equation of the family of all circles which pass through the origin and whose centre lie on y-axis. |
|
Answer» |
|
| 196. |
Let f:[0,1] rarr R be a function . Suppose the fuction f is twice differentiable with f(0) =f(1)=0and satisfies f(x)-2f(x)+f(x) ge e^x " for all " x in [0,1].Which of the following is true for x in (0,1] ? |
|
Answer» `0 lt F(x) lt oo` `f''(x)-2f(x)+f(x) ge E^x " for all " x in [0,1]` `e^(x)f''(x)-2f''(x)e^(-x)+f(x)e^(-x)f(x)e^(-x)ge 1 " for all " x in [0,1]` `rArr {e^(-x) f''(x) -e^(-x)f(x)}-{-e^(-x))ge 1 " for all " x in [0,1]` `rArrd/(dx) f(x)e^)(-x)-f(x)e^(-x) ge 1 " for all " x in [0,1]` `rArr d/dx{d/dx f(x)e^(-x)} ge 1 " for all " x in [0,1]` `rArr d^2/dx^2(f(x)d^(-x) ge 1 " for all " x in [0,1]` `rArrd^2/dx^2( PHI (x))ge 1 " for all " x in [0,1] " where " phi (x)=f(x)e^(-x)` `rArr(x) ` is concave UPWARD on [0,1] It is given that f(0)=f(1)=0. Therefore`phi(0)= phi(1)=0` Therefore `phi(x)lt 0 " for all" x in (0,1) rArr - oo lt f(x) lt 0 " for all " x in (0,1)` |
|
| 197. |
Method of integration by parts : If int(e^(x)(1+sinx)dx)/(1+cosx)=e^(x)f(x)+c, then f(x)= |
|
Answer» `"sin"(x)/(2)` |
|
| 198. |
Evalute the following integrals int (x^2)/((x^(2) + 4)(x^(2) + 9))dx |
| Answer» | |
| 199. |
{:("Column A","", "Column B"),("The perimeter of"DeltaABC,,"The The circumference of the circle"):} |
|
Answer» If column A is LARGER |
|
| 200. |
Using properties of determinants in Exercise 11 to 15 prove that |{:(x,x^2,1+px^3),(y,y^2,1+py^3),(z,z^2,1+pz^3):}|=(1+pxyz)(x-y)(y-z)(z-x) |
|
Answer» |
|