Explore topic-wise InterviewSolutions in .

This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.

101.

Let bar(a) = 2bar(i) + 3bar(j) + bar(k), bar(b) = 4bar(i) + bar(j) and bar(c ) = bar(i) - 3bar(j) -7bar(k). Find the vector bar(r )such that bar(r ).bar(a) = 9, bar(r ).bar(b) = 7 and bar(r ).bar(c ) =6.

Answer»


Answer :`bar(R ) = bar(i) + 3BAR(J) - 2bar(k)`
Discussion
102.

Critical points of y=a log x + bx^(2)+x are x=-1 and x = 2. Then find a and b.

Answer»


ANSWER :`a = 2, B=-(1)/(2)`
Discussion
103.

Find the values of a for whch sin^*(-1)x=|x-a| will have at least one solution.

Answer»

Solution :
(i) When `alt0`
In this CASE, y = a-x MUST pass through `(1,pi/2)`
`thereforepi/2=a-1rArra=1+pi/2`
(II) When `alt0`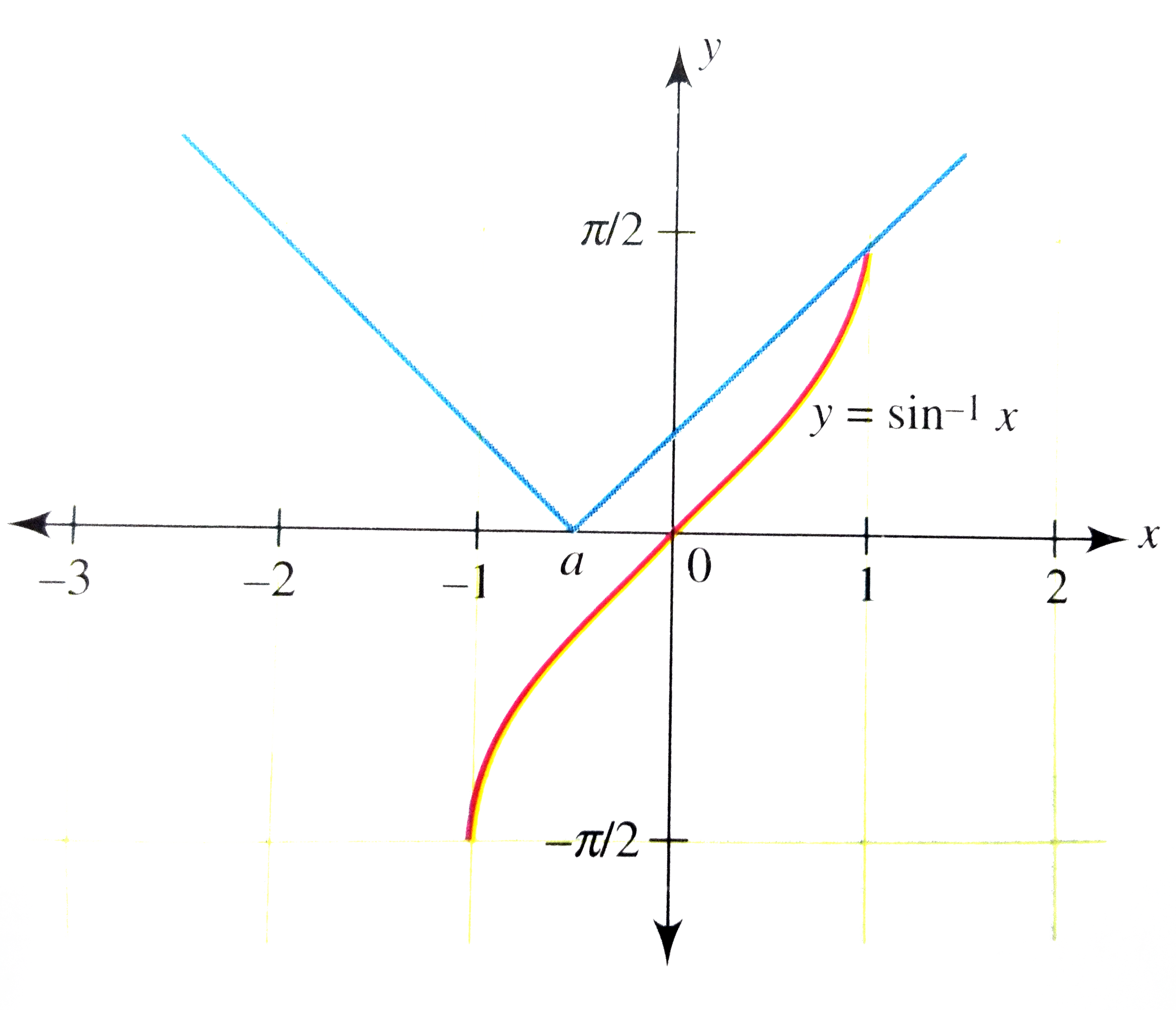

In this case,
`y=x-a" must pass THOUGH "(1,pi/2)`
`pi/2=1-a`
`a=1-pi/2`
For at least on solution.
`1-pi/2leale1+pi/2`
Discussion
104.

Find the vector equation of the line that passes through the points (3,-2,-5)and(3,-2,6)

Answer»

`barr=hati+2hatj+3hatk+lambda(3hati-2hatj-5hatk)`
`barr=-3hati-2hatj-6hatk+lambda(11hatk)`
`barr=3hati-2hatj-5hatk+lambda(11hatk)`
`barr=hati-2hatj+3hatk+lambda(3hati-2hatj+6hatk)`

ANSWER :C
Discussion
105.

If the normals at the four points (x_1,y_1),(x_2,y_2),(x_3,y_3) and (x_4,y_4) on the ellipse x^(2)/a^(2)+y^(2)/b^(2)=1 are concurrent. Prove that (x_1+x_2+x_3+x_4)((1/x_1+1/x_2+1/x_3+1/x_4)=4

Answer»
Discussion
106.

I= int cos ("In" x) dx.

Answer»


ANSWER :`I= (X)/(2) [ COS ("In" x) + sin ("In" x)]+ C`.
Discussion
107.

If a**b = a +b - abon Q^(+) , then the identity and the inverse of a for ** are respectively ..........

Answer»

`0 and (a)/(a-1)`
`1 and (a-1)/a`
`-1 and a`
`0,(1)/a`

SOLUTION :N/A
Discussion
108.

If A=[{:(0,-1,2),(4,3,-4):}]andB=[{:(4,0),(1,3),(2,6):}]then verify that : (i) (A')=A (ii)(A*B)'=B'*A' (iii)(kA)'=(k*A')

Answer»


ANSWER :`=KA`'
Discussion
109.

In the physics lab, a student determined the kinetic energy, KE, of an object at various velocities, V, and found a strong positive association between KE and V. Which of the above scatterplots show this relationship?

Answer»

GRAPH (1)
Graph (2)
Graph (3)
Graph (4)`

Answer :B
Discussion
110.

Examine thatf(x) = sin |x| is a continuous function.

Answer»


ANSWER :f(X) is ALSO everywhere CONTINUOUS.
Discussion
111.

Find all the three digit numbers for which one obtains when dividing the number by 11, the sum of the squares of the digits of the initials.

Answer»


ANSWER :550803
Discussion
112.

Let ABCD be a parallelogram whose equations for the diagonals AC and BD are x+2y=3 and 2x+y=3, respectively. The length of side AB is equal to

Answer»

`2sqrt(58)//3`
`4sqrt(58)//9`
`3sqrt(58)//9`
`4sqrt(58)//9`

Solution :`"cos" (pi-theta) = (AP^(2) + PB^(2)-AB^(2))/(2AP xx PB)`
`"or " -(4)/(5) = (4+(100//9)-AB^(2))/(2 xx 2 xx (10//3))`
`"or " AB = (2sqrt(58))/(3)`
Discussion
113.

Write the vale of intxa^(x^(2+1))dx

Answer»

SOLUTION :`INTXA^(x^2+1)dx=1/2inta^tdt` (Where`x^2+1=timplies2xdx=dt) =a^t/(2Ina)+C`
Discussion
114.

Equation to the circles which pass through the point (2,3) and cut off equal chords of length 6 units along the lines y-x-1=0 and y+x-5=0 is

Answer»

`(x-3)^2+(y-2sqrt3)^2=(3sqrt2)^2`
`(x-2)^2+(y-3-3sqrt2)^2=(3sqrt2)^2`
`(x-2sqrt3)^2 + (y-3)^2 =(3sqrt2)^2`
`NONE of these

ANSWER :B
Discussion
115.

If z‌_(1), z_(2), z_(3) , z_(4) are the affixes of the vertices of a parallelogram taken in order in Argand plane, then

Answer»

`z_(1)+z_(3)=z_(2)+z_(4)`
`z_(1)+z_(2)=z_(3)+z_(4)`
`z_(1)-z_(3)=z_(2)-z_(4)`
None of these

Answer :A
Discussion
116.

If the system of linear equations above has o solution, and a is a constant, then what is the value of a ?

Answer»

`-2`
`-1/2`
`2`
6

Solution :Graphically, a system of linear equations that has no solution INDICATES two parallel lines-that is, two lines that have the same slope but different y-intercepts. To have the same slope, the x-and y-coefficient must be the same. To get from `-2/3` to `-8,` you multiply by 12, so multiply `-1/2x ` by 12 as well to yield 6x. Because the other x-coeffieient is a, it must be that `a =6,` and (D) is correct. Note that, even though it is more work, you could ALSO write each EQUATION in slope-intercept FORM and SET the slopes equal to each other to solve for a.
Discussion
117.

int_(log2)^(t)(dx)/(sqrt(e^(x)-1))=(pi)/(6), then t=

Answer»

LN 8
ln 6
ln 4
1

Answer :C
Discussion
118.

If the d.c.'s (l, m, n) of two lines are connected by the relations l+m+n=0 " and " 2mn+3ln-5lm=0 then the angle between the lines is

Answer»

`pi//4`
`pi//3`
`pi//6`
`pi//2`

ANSWER :D
Discussion
119.

Find the number of positive integral solutions of x_(1)x_(2)x_(3)=54 where x_(1),x_(2),x_(3)ne1

Answer»


ANSWER :9
Discussion
120.

Match the following. {:(,"List -I",,"List-II",),(,"(Differential equation)",,"(Order O, Degree = D)",),((1),[((dy)/(dx))^(3)+(d^(2)y)/(dx^(2))]^(2) = a(dy)/(dx),(a),2O + 3D = 8,),((2),3y = 7x(dy)/(dx)+(5)/(dy//dx),(b),O^(D)+D^(O) = 4,),((3),(d^(2)y)/(dx^(2)) - 5(dy)/(dx)+6y = 0,(c) ,O=D,),((4),((dy)/(dx)+4x)^(3//2) = x+5(dy)/(dx),(d),3^(O)+2^(D) = 11,):} The correct match from List-I from List -II

Answer»

1-a, 2-C, 3-b, 4-d
1-b, 2-d, 3-c, 4-a
1-c, 2-a, 3-d, 4-b
1-d, 2-b, 3-a, 4-c

Answer :C
Discussion
121.

There are three bags B_1,B_2 and B_3. The bag B_1 contains 5 red and 5 green balls, B_2 contains 3 red 5 green balls, and B_3 contains 5 red and 3 green balls. Bags B_1, B_2 and B_3 have probabilities (3)/(10),(3)/(10) and (4)/(10) respectively of being chosen. A bag is selected at random and a ball is chosen at random form the bag. then which of the following options is/are correct ?

Answer»

Probability that the CHOSEN ball is green, GIVEN that the selected bag is `B_3` equals `(3)/(8)`.
Probability that the selected bag is `B_3` , given that the chosen ball is green equals `(5)/(13)` .
Probability that the chosen ball is green equals `(39)/(80)` .
Probability that the selcted bag is `B_3` and the chosen ball is green equals `(3)/(80)`

Solution :Key Idea : Use conditional probability. Total probability and Baye's theorem.
It is given that there are three bags, `B_1,B_2` and `B_3` and probabilities of being chosen, `B_1,B_2 and B_3` are RESPECTIVELY.
`THEREFORE P(B_1)=(3)/(10),P(B_2)=(3)/(10) and P(B_3)=(4)/(10)`
Now, probability that the chosen ball is green, given that selected bag is `B_3P((G)/(B_3))=(3)/(8)`
Now, probability that the chosen selected bag is `B_3`, given that the chosen ball is green `=P((B_3)/(G))`
`=(P((G)/(B_3))P(B_3))/(P((G)/((B_1))P(B_1))+P((G)/(B_2))P(B_2)+P((G)/(B_3))P(B_2))["by Baye's theorem"]`
`=(((3)/(8)xx(4)/(10)))/(((5)/(10)xx(3)/(10))+((5)/(8)xx(3)/(10))+((3)/(8)xx(4)/(10)))=((1)/(2))/((1)/(2)+(5)/(8)+(1)/(2))=(4)/(13)`
Now, probability that the chosen ball is green `=P(G)=P(B_1)P((G)/(B_1))+P(B_2)P((G)/(B_2))+P(B_3)P((G)/(B_3))`
[By using theorem of total probability]
`=((3)/(10)xx(5)/(10))+((3)/(10)xx(5)/(8))+((4)/(10)xx(3)/(8))`
`=(3)/(20)+(3)/(16)+(3)/(20)=(12+15+12)/(80)=(39)/(80)`
Now, probability that the selected bag is `B_3` and the chosen ball is green `=P(B_3)xxP((G)/(B_3))=(4)/(10)xx(3)/(8)=(3)/(20)`
Hence, OPTIONS (a) and (c) is are correct.
Discussion
122.

Find the period of cos^(4)x.

Answer»

`PI`
`2PI`
`pi//2`
`3PI`

ANSWER :A
Discussion
123.

If y = sum_(n=2)^(oo) (""^nc_2 .(3^(n-2))/(n!)) then 2y =

Answer»

E
`e^2`
`e^3`
`e^4`

ANSWER :C
Discussion
124.

If O is the origin and A is (a, b, c), then find the direction cosines of the line OA and the equation of plane through A at right angle to OA.

Answer»


ANSWER :`THEREFORE ax+by+cz=a^2+b^2+c^2`
Discussion
125.

Evalute the following integrals int (5x^(4) + 7)dx

Answer»


ANSWER :`X^(5)+7x+c`
Discussion
126.

Findthe value of a,b,cand d. [{:(a,3a-b),(2a+c,3b-d):}]=[{:(3,2),(7,7):}]

Answer»


ANSWER :`a=3,b=7,c=1,d=14`
Discussion
127.

(vec(a).hat(i))hat(i)+(vec(a).hat(j))hat(j)+(vec(a).hat(k))hat(k)=

Answer»

0
`VEC(a)`
`2vec(a)`
`3vec(a)`

ANSWER :B
Discussion
128.

If a line has direction cosines 2/3,-1/3,-2/3, then find its direction.

Answer»


ANSWER :2,-1,-2
Discussion
129.

If side of a cube is 10 cm and error in it is 0.05 cm then match the following {:("I.","Error in surface are of cube","a",15),("II".,"Percentage error in surface area",b,6),("III.","Error in volume",c,1.5),("IV.","Percentage error in volume",d,0.05),("","",e,1):}

Answer»

B,d,E,a
a,c,c,d
a,c,b,e
b,e,a,c

Answer :D
Discussion
130.

If a,b,c are three consevutive terms of an AP and x,y,z are three consecutive terms of a GP, then the value of X^(b-c).Y^(c-a). Z^(a-b) is

Answer»

1)0
2)xyz
3)-1
4)1

Answer :D
Discussion
131.

Evaluate the following determinates |{:(sin10^@,-cos10^@),(sin80^@, cos80^@):}|

Answer»


ANSWER :1
Discussion
132.

If ABCD is a cyclic quadrilateral with AB = 6, BC = 4, CD = 5, DA= 3 and angleABC = theta ,then cos theta=

Answer»

A`(3)/(13)`
B`(18)/(76)`
C`(16)/(78)`
D`(78)/(86)`

ANSWER :A
Discussion
133.

A circle having centre as O' and radius r' touches the incircle of Delta ABC externally at. F, where F is on BC and also touches its circumcircle internally at G. It O is the circumcentre of Delta ABC and I is its incentre, then

Answer»

OO'=R-r'
Perpendicular distance from O to line joining IO' is `|(b-c)/(2)|`
Projection of OO' on line joining IO'=r'+R cos A
`r'=(DELTA)/(a)tan^(2)A`

SOLUTION :From FIGURE, OO' = OG - O'G = R-r'

`OE=DE=|BF-BD|=|s-b-(a)/(2)|=(|c-b|)/(2)`
OD = EF = R cos A
From `Delta OEO'`, using Pythagoras theorem, we get
`(R-r')^(2)=(R cos A+r')^(2)+((c-b)/(2))^(2)`
`rArr r' =(BC)/(4R)"tan"^(2)(A)/(2)`
`= (Delta)/(a)"tan"^(2)(A)/(2)`
Discussion
134.

The value of ("sin"(2019pi)/2-cos2019pi)/("tan"(2020pi)/3) is

Answer»

1
-1
0
`SQRT3`
Discussion
135.

Differentiate cotx^2

Answer»

SOLUTION :LET `y=cotx^2`
Then `dy/dx=-"COSEC"^2x^2xxd/dx(x^2)`
`=-"cosec"^2x^2 cdot2x`
`=-2xcdot "cosec"^2x^2`
Discussion
136.

int_(0)^(pi/4) sin 2x dx

Answer»

SOLUTION :`" Let I "= int_(0)^(pi//4) sin 2 x dx`
`=int_(0)^(pi//4) 2 sin x COSX dx `
`UNDERSET(x=0 ""rArr t=sin 0=0)underset(x=(pi)/(4) ""rArr t= sin.(pi)/(4) =(1)/(SQRT(2)))("Letsin "x=t ""rArr cosx dx =dt)`
`:. I=2 int_(0)^(pi//sqrt(2))t dt = 2 [(t^(2))/(2)]_(0)^(1//sqrt(2))`
`=((1)/(sqrt(2)))^(2)=(1)/(2)`
Discussion
137.

Let u,v,w be rela numbers in geometric progression such that u gt v gt w. Suppose u ^(40)= v ^(n) = w ^(60). Find the value of n .

Answer»


ANSWER :48
Discussion
138.

Refers to question 27. Maximum of Z occurs at

Answer»

(5,0)
(6,5)
(6,8)
(4,10)

Solution :Refers to solution 27, MAXIMUM of Z occurs at (5,)
Discussion
139.

Integrate thefunction in Exercise. (x^(3)-1)^((1)/(3))x^(5)

Answer»
Discussion
140.

If x(hat(i) + hat(j) + hat(k)) is a unit vector then x equals ?

Answer»

`(1)/(SQRT(3))`
`PM sqrt(3)`
`sqrt(3)`
`pm (1)/(sqrt(3))`

ANSWER :D
Discussion
141.

The sum to n terms of the series 1 + (1 + 3) + (1 + 3 + 9) + (1 + 3 + 9 + 27)+ .......... is

Answer»

`(3(3^(n) - 1))/4 - 1`
`(3(3^(n) - 1) - 2n)/4`
`(3(3^(n) - 1) - n)/4`
`(2n - 3(3^(n) - n))/4`

ANSWER :B
Discussion
142.

Centre and radius of the circle with segment of the line x+y=1 cut off by coordinate axes as diameter is

Answer»

`(1/2,1/2),1/(SQRT(2))`
`(-1/2,-1/2),(1/(sqrt(2)))`
`(1/2,-1/2),1/(sqrt(2))`
`(-1/2,1/2),1/(sqrt(2))`

ANSWER :A
Discussion
143.

The order and degree of the differential equation [((dy)/(dx))^(2) + ((d^(2)y)/(dx^(2)))]^(5//4) = k (d^(3) y)/(dx^(3)) is

Answer»

1,2
2,3
3,4
4,5

Answer :C
Discussion
144.

Integrate the following functions : intcosecx.log(cossex-cotx)dx

Answer»


ANSWER :`(1)/(2)[log|cosecx-cotx|]^(2)+C`
Discussion
145.

Let Abe a square matrix of order 3xx3, then |KA| is equalto

Answer»

` K|A| `
` k^(2) |A| `
` k^(3) |A| `
` 3K |A| `

ANSWER :C
Discussion
146.

If f:RtoRandg:RtoR are given by f(x)=cosxandg(x)=3x^(2). Find gof and fog.

Answer»


ANSWER :`COS(3X^(2))`
Discussion
147.

int_(0)^(pi//2)x sin x dx =

Answer»

0
1
-1
2

Answer :B
Discussion
148.

{:(I."The points" i + j + k. 4i + 3j "and" 10 i + 7j - 2k "are", a. a xx b = 7c),(II. "The vectors" 5i + 5j + 7k. 7i - 8j + k "and" i - 20 j - 5k "are",b. "collincar"),(III. a = 2i + 3j + 6k. b = 3i - 6j + 2k, c. "non-coplanar"),(IV. "The Points" 2i - j + k. i - 3j = 5k "and" 3i - 4j - 4k "are", d."vertices of equilateral triangle"),(, e. "vertices of right angled triangle"):}

Answer»

B,C,a,e
a,c,d,e
a,c,b,e
e,d,c,a

Answer :A
Discussion
149.

If the vectors veca = 2hati + 3hatj +-6hatk and vecb = alphahati-hatj +2hatk are parallel, then alpha = ______

Answer»

2
44257
-2/3
44256

Answer :C
Discussion
150.

Find the non-parametric form of vector equation, and Cartesian equation vector equation, and Cartesian equation of the plane passing through the point (0, 1,-5) and parallel to the straight linesvecr=(hati=2hatj-4hatk)+s(2hati+3hatj+6hatk)andvecr=(hati=3hatj-4hatk)+t(hati+hatj+hatk)

Answer»


Answer :`(vecr-veca).(vecb XX VEC c)=0`, 9x-8y+z+13=0
Discussion