Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 51. |
Sum of all terms in in G.P is 5 times the sum of odd terms. The common ratio is |
|
Answer» 2 |
|
| 52. |
For a real number r let [r] denote the largest integer less than or equal to r. Let agt1 be a real number which is not an integer and let k be the smallest positive integer positive integer such that [a^(k)]gt[a]^(k). Thenwhich of the following statements is always true? |
|
Answer» `kle2([a]+1)^(2)` options (B) is possible. |
|
| 53. |
If bara,barb and barc are non coplanar vectors such that barb times barc=barb then |
|
Answer» `|bara|=1` |
|
| 54. |
A line y=mx +1 intersects the circle (x-3)^2+(y+2)^2=25 at the points P and Q . If the midpoint of the line segment PQ has x-coordinate -(3)/(5), then which one of the following options is correct ? |
|
Answer» `6 le m LT 8` It is given that points P and Q are intersecting points of circle. `(x-3)^2+(y+2)^2=25` .....(i) Line `"" y=mx+1 "".....(ii)` And , the mid -point of PQ is A having x-coordinate `(-3)/(5)` so y-coordinate is `1-(3)/(5)m`. So, `A(-(3)/(5),1-(3)/(5)M)` From the figure, `because AC BOT PQ` 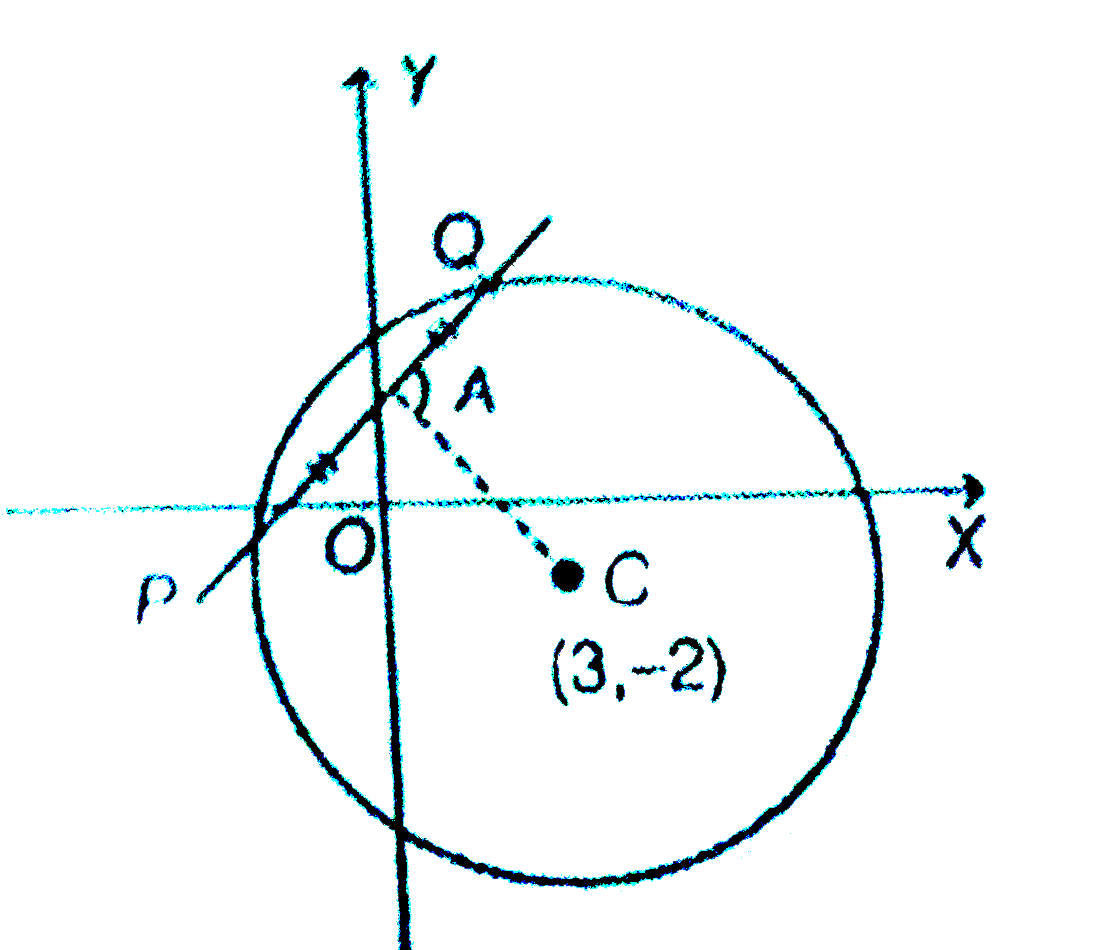 `rArr` (slope of AC)x (slope of PQ)` =-1`. `rArr ((-2-1+(3)/(5m))/(3+(3)/(5)))xxm=-I` `rArr 3m^2-15m+18=0` `rArr m=2or 3`. |
|
| 55. |
If the median of the data 6,7,x-2,x,18 and 21 written in ascending order is 16, then the variance of that data is |
|
Answer» `30(1)/(5)` |
|
| 56. |
In the experiment of tossing a coin n times, if the variable X denotes the number of heads and P(X=4),P(X=5),P(X=6) are in arithmetic progression then find n. |
|
Answer» 11 |
|
| 57. |
Assuming the validity of the operations on the r.h.s. find dy/dt y = sqrt[[sin x + sqrt{{sin x + sqrt((sin x + ........)}])}] |
|
Answer» SOLUTION :`y = {sqrt [SIN + sqrt {sin x +1........]}}` sqrt(sin x + y) IMPLIES y^2 + sin x + y implies 2Y (dy)/(DX) = cos x + dy/dx implies (2y-1) dy/dx = cos x implies dy/dx = cos x/(2y-1)` |
|
| 58. |
The value of P for which both the roots of the equation4x^(2)-20Px +(25P^(2)+15P-66)=0 are less than 2, lies in |
| Answer» Answer :d | |
| 59. |
Evaluate the following determinates |{:(1,omega),(omega,-omega):}| where omega is the cube root of unity |
|
Answer» |
|
| 60. |
If the lines x-2y+3=0, 3x+ky+7=0 cut the coordinate axes in concylic points, then k= |
|
Answer» only I |
|
| 61. |
The tangent at a point P on the ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2))=1 meets directrics at Q and Q. A circle is drawn assuming PQ as diameter. Statement-1 This circle passes through the foci of the ellipse because Statement-2 PQ subtends 90^(@) at the corresponding focus. |
|
Answer» Statement 1 is True, Statement -2 is True, Statement -2 is a CORRECT exlpanation for Statement 1 |
|
| 62. |
If A = [(0,1),(1,0) ]then A^(2) is equal to : |
|
Answer» `[(0,1),(1,0)]` |
|
| 63. |
If (1+x)^(n) = C_(0) + C_(1)x + C_(2)x^(2) + "….." + C_(n)x^(n), then C_(0) - (C_(0) + C_(1)) +(C_(0) + C_(1) + C_(2)) - (C_(0) + C_(1) + C_(2) + C_(3))+"….."(-1)^(n-1) (C_(0) + C_(1) + "……" + C_(n-1)) is (where n is even integer and C_(r) = .^(n)C_(r)) |
|
Answer» a positive value `C_(0)-(C_(0)+C_(1))+(C_(0)+C_(1)+C_(2))-(C_(0)+C_(1)+C_(2)+C_(3))+"....."(-1)^(n-1)(C_(0)+C_(1)+"....."+C_(n-1))` `= C_(0)-(C_(0)+C_(1))+(C_(0)+C_(1)+C_(2))-(C_(0)+C_(1)+C_(2)+C_(3))+"....."-(C_(0)+C_(1)+"...."+C_(2m-1))` `= - (C_(1)+C_(3)+C_(5)+"...."+C_(2m-1))` `= - (C_(1)+C_(3)+C_(5)+"......."+C_(n-1)) = -2^(n-1)` |
|
| 64. |
If the remainders obtained when a polynomial f(x) is divided with x, x-1, x+1 respectively are 1, -2, 3 then find the remainder when f(x) is divided with x^(3)-x ? |
|
Answer» |
|
| 65. |
Compute the following : (i) [{:(a,b),(-b,a):}]+[{:(a,b),(b,a):}] (ii) [{:(a^(2)+b^(2),b^(2)+c^(2)),(a^(2)+c^(2),a^(2)+b^(2)):}]+[{:(2ab,2bc),(-2ac,-2ab):}] (iii)[{:(-1,4,-6),(8,5,16),(2,8,5):}]+[{:(12,7,6),(8,0,5),(3,2,4):}] (iv) [{:(cos^(2)x,sin^(2)x),(sin^(2)x,cos^(2)x):}]+[{:(sin^(2)x,cos^(2)x),(cos^(2)x,sin^(2)x):}] |
|
Answer» (II) `=[{:((a+b)^(2),(b+c)^(2)),((a-c)^(2),(a-b)^(2)):}]` (III) `=[{:(11,11,0),(16,5,21),(5,10,9):}]` (IV) `=[{:(1,1),(1,1):}]` |
|
| 66. |
The world bank measures the amount of land devoted to agriculture among all 196 countriesin the world. The results from 9 of the countries are given in the table above. The median percent of of agrilcultural land for all 196 countriesin 34.95%. What is the difference between the median percent of agricultural land for these 9 countries and the median for all 196 countries? |
|
Answer» 0.0115 |
|
| 68. |
Evaluate : (i) Lim_(nrarroo) sum_(r=0)^(nrarr1) (1)/(sqrt(n^(2)-r^(2))) , (ii)Lim_(nrarroo) 3/n[1+sqrt((n)/(n+3))+sqrt((n)/(n+6))+sqrt((n)/(n+9))+"....."+sqrt((n)/(n+3(n-1)))] (iii) lim_(nrarroo) (sum_(r=1)^(2n) (3nr^(2)+2n^(2)r)) |
|
Answer» |
|
| 69. |
A pair of dice is rolled. What is the probability that neither die shows a 2 given that they sum to 7. |
|
Answer» |
|
| 70. |
How many 4 digit numbers are there, without repetition of digits, If each number is divisible by 5 ? |
|
Answer» |
|
| 71. |
Reshma wishes to mix types of food P and Q in such a way that the vitamin contents of the mixture contain at least 8 units of vitamin A and 11 units of vitamin B. Food P costs Rs. 60/kg and Food Q costs Rs. 80/kg. Food P contains 3 units/kg of vitamin A and 5 units/kg of Vitamin B while food Q contains 4 units/kg of Vitamin A and 2 units/kg of vitamin B. Determine the minimum cost of the mixture. |
|
Answer» |
|
| 72. |
If (1+x+x^2+____x^100) (1-x+x^2-x^3+___+x^150) =a_0+a_1x+a_2x^2+____ +a_250 x^250 Then the value of a_0+a_2 + a_4+____ + a_250 is equal to ___ |
|
Answer» Put x=-1 we get `1xx151=a_0-a_1+a_2` ___`a_250` `252=2(a_0+a_2+____a_250)` `a_0+a_2+a_4`+___+`a_250`= 126 |
|
| 73. |
If log_(e)5, log_(e)(5^(x) -1) and log_(e)(5^(x)-(11)/(5)) are in A.P then the values of x are |
|
Answer» `log_(5) 4 and log_(5)3` |
|
| 74. |
Three numbers are chosen at random without replacement from {1,2,3,….8}. The probability that their minimum is 3, given that their maximum is 6, is |
|
Answer» `(3)/(8)` |
|
| 75. |
Let W(x,y) =x ^(2) + xy+y ^(2) and x = sin t, y = cos t in t in (0, 2pi) verify the above theorem. |
|
Answer» |
|
| 76. |
Compute the length of the segment of the straight line rho= a sec (varphi- (pi)/(3)) between varphi= 0 and varphi=(pi)/(2) |
|
Answer» |
|
| 77. |
If veca=(3hati-hatj)/(sqrt(10)) and vecb=(hati+3hatj+hatk)/(sqrt(11)), then the value of (2veca+vecb)".[(veca xx vecb)xx(veca-3vecb)] |
|
Answer» 5 |
|
| 78. |
Integrate the following functions (sin^-1x)^2 |
|
Answer» Solution :`INT (sin^-1 x)^2 DX = int 1 XX (sin^-1 x)^2 dx` =`(sin^-1 x)^2X- int 2 sin^-1 x 1/sqrt(1-x^2) x dx` =`x (sin^-1x)^2 + int (-2x)/sqrt(1-x^2) xx sin^-1x dx` =`x (sin^-1x)^2+ int (-2x)/sqrt(1-x^2) dx - int (1/sqrt(1-x^2) int (-2x)/sqrt(1-x^2) dx) dx` =`x(sin^-1x)^2+ sin^-1x xx 2 sqrt(1-x^2)- int1/sqrt(1-x^2) 2sqrt(1-x^2) dx` =`x (sin^-1 x)^2 +2 sqrt(1-x^2) sin^-1 x- 2x+c` |
|
| 79. |
Refers to question 15.Determine the maximum distance that the man can travel. |
Answer»  MAXIMISE Z=x+y subject to `2x+3y le 120, 8x+5y le 400, x ge 0, y ge 0` On solving we get `8x +5y=400 and 2x+3y=120 we get ` `(30)/(7),(80)/(7)` and (0,40)  HENCE the maximum distance that the man can TRAVEL is `54(2)/(7)KM`. |
|
| 80. |
int e^(2x) (2sinx + cosx) dx = |
|
Answer» `e^(2x)` SINX + C |
|
| 81. |
If A+B+C=90^(@) then (cos 2A+cos 2B+cos 2C-1)/(sin A sin B sin C)= |
|
Answer» 2 |
|
| 82. |
If int(dx)/(1+e^(x))=x+f(x)+C , then f(x) is equal to |
|
Answer» `log (1 + E^(x))` |
|
| 83. |
The mid point of the chord x+2y+3=0 of the hyperbola x^(2)-y^(2)=4 is |
| Answer» ANSWER :D | |
| 84. |
At what points in the interval [0, 2pi], does the function sin (2x) attain its maximum value ? |
|
Answer» |
|
| 85. |
If the angle between the two equal circles with centres (-2,0),(2,3) is 120^@then the radius of the circle is |
|
Answer» 5 |
|
| 86. |
If bar(a) = overset(^)(i) + overset(^)(j) - overset(^)(k), bar(b) = 2 overset(^)(i) + 3 overset(^)(j) + 2 overset(^)(k), bar(c ) = - overset(^)(i) + overset(^)(j) +3 overset(^)(k) then the volume of tetrahedron is |
| Answer» Answer :A | |
| 87. |
The tangents drawn from the origin x^(2)+y^(2)-2rx-2hy+h^(2)=0 are per-pendicular if |
|
Answer» `H=R+1` |
|
| 88. |
The real values of 'a' for which the quadratic equation 2x^2 - (a^3 + 8a - 1) x + a^2 - 4a = 0 possess roots of opposite sign is given by: |
|
Answer» |
|
| 89. |
In the spacethe equationby + cz + d = 0represents a plane perpendicular to the |
|
Answer» YOZ - PLANE |
|
| 90. |
k-^n C_1 (k-1)+^n C_2 (k-2)-…..+(-1)^n ""^n C_n (k-n)= |
|
Answer» 0 |
|
| 91. |
Locus of perpendicular from center upon normal to the hyperbola (x^(2))/(a^(2)) -(y^(2))/(b^(2)) =1 is |
|
Answer» `(x^(2)-+y^(2))^(2)((a^(2))/(x^(2))+(b^(2))/(y^(2))) =(a^(2)-b^(2))^(2)` `(y-k) =- (h)/(k) (x-h)` or `HX + ky = h^(2) +k^(2)` (1) Also normal at any point `R(a sec theta, tan theta)` on the hyperbola is `(ax)/(sec theta) +(by)/(tan theta) = a^(2) + b^(2)` (2) Comparing ratio coefficients of equations (1) and (2), We get `((a)/(sec theta))/(h)=((b)/(tan theta))/(k) =(a^(2)+b^(2))/(h^(2)+k^(2))` `rArr sec theta = (a(h^(2)+k^(2)))/(h(a^(2)+b^(2)))` and `tan theta = (b(h^(2)+k^(2)))/(k(a^(2)+b^(2)))` Squaring and subtracting `(x^(2)+y^(2))^(2) ((a^(2))/(x^(2))-(b^(2))/(y^(2))) = (a^(2)+b^(2))^(2)` |
|
| 92. |
If a,b,c are rational , the roots of equationx^2-2ax+(a^2-b^2+2bc-c^2)=0 are : |
|
Answer» RATIONAL |
|
| 93. |
Match the following. I. int (1)/(sqrt(4-x^(2)))dx= "" a) (1)/(2) Sinh^(-1))(x)/(2)+c II. int (1)/(sqrt(4+x^(2)))dx= "" b)Cosh^(-1)(x)/(2)+c III. int (1)/(x^(2)-4))dx= "" c) "Sin"^(-1)(x)/(2)+c |
|
Answer» a,B,c |
|
| 94. |
|{:(sin35^@,-cos35^@),(sin55^@,cos55^@):}|=......... |
|
Answer» 1 |
|
| 95. |
A vector vecr is inclined to x-axis at 45^(@) and to y-axis at 60^(@). If |vecr|=8 units find vecr. |
|
Answer» |
|
| 96. |
The scatterplot above shows the numbers of people diagnosed with melanoma, in ten - thousands, from 1940 to 1970. Based on the data shown in the figure, which of the following values is closest to the range of the number of incidences of melanoma between 1945 and 1950? |
|
Answer» 5000 |
|
| 97. |
Given PV=C (constant). The percentage of increase in V corresponding to an increase 1% in the value of P is |
|
Answer» 0 |
|
| 98. |
A bag contain 6 white and 4 red balls if 3 balls are drawn at random the probability of getting 1 red ball and 2 white balls is |
|
Answer» `1/2` |
|
| 99. |
Find the value of the integral underset(-pi//2)overset(pi//2)int sin^(2) theta . Cos^(7)theta d theta |
|
Answer» |
|
| 100. |
Evalute the following integrals int (1)/(x) sqrt((x - 1)/(x + 1))dx = |
|
Answer» `cosh^(-1)X - sec^(-1) ` x + C |
|