28278 + Interview Questions in Maths in Class 12 Page 85 InterviewSolution

4201.	A positive divisor of 1800 is selected at random and given that the selected divisor is a multiple of 10. Find the probability that it is a multiple of 25.
Answer» ANSWER :`(1)/(2)`

Discussion

4202.	Evalute the following integrals int sqrt(1 + 3x - x^(2)) dx
Answer» `(2x - 3)/(4) sqrt(1 + 3X -x^(2)) + (13)/(8) SIN^(-1) ((2x - 3)/(sqrt(13))) + c` `(2x - 3)/(4) sqrt(1 + 3x - x^(2)) -(13)/(8) sin^(-1) ((2x - 3)/(sqrt(13))) + c` `(2x + 3)/(4) sqrt(1 + 3x - x^(2)) -(13)/(8) sin^(-1) ((2x - 3)/(sqrt(13))) + c` `(2x + 3)/(4) sqrt(1 + 3x - x^(2)) + (13)/(8) sin^(-1) ((2x - 3)/(sqrt(13))) + c` ANSWER :A

Discussion

4203.	Complex numbers z satisfy the equaiton \|z-(4//z)\|=2 Locus of z if \|z-z_(1)\| = \|z-z_(2)\|, where z_(1)and z_(2) are complex numbers withthe greatest and the least moduli, is
Answer» lineparallel to the real axis line parallel to the IMAGINARY axis line havinga positive slope line havinga negativeslope Solution : We have `\|\|z\|-\|4/z\|\| le \|z-4/5\|=2` `rArr -2 le \|z\| - 4/\|z\| le 2 ` `rArr \|z\|^(2) +2 \|z\| -4 GE0 ` and `\|z\|^(2) -2\|z\|-4 le 0` ` rArr (\|z\|+1)^(2)-5 le 0 ` and `(\|z\|-1)^(2) le 5` `rArr (\|z\|+1 + sqrt(5)) (\|z\|+1-sqrt(5)) ge0` `rArr \|z\| ge sqrt(5) -1` and `(\|z\|- 1+sqrt(5)) xx(\|z\|-1-sqrt(5)) le 0` `rArr sqrt(5)-1 le \|z\| ge sqrt(5)-1` and `(\|z\| -1 + sqrt(5)) (\|z\| -1-sqrt(5)) le0` `rArrsqrt(5)-1 le \|z\| le sqrt(5)+1` `rArr sqrt(5) -1 le \|z\| le sqrt(5)+1 ` Hence, the LEAST modulus is `sqrt(5)-1` and the greatest modulus is `sqrt(5) +1`. also, `\|z\|=sqrt(5) +1 ` `rArr 4/(\|z\|) =sqrt(5)-1` Now `4/z =(4bar(z))/(\|z\|^(2))` Hence, `4//z` lies in the direction of `bar(z)` `\|z-4/z\|=PR=2 ` (given ) We have `OP =sqrt(5) +1 ` and `OR =sqrt(5)-1` `rArr cos 2 theta=(OP^(2)+OR^(2)+PR^(2))/(2OP.OR)` `=((sqrt(5)+1)^(2)+(sqrt(5)-1)^(2)-4)/(2(5-1))=1` `rArr 2 theta=0, 2pi` `rArr theta=0, PI` `rArr z ` is purely real `rArrz=pm(sqrt(5)+1)` similarly for \|z\| =sqrt(5)-1` , we have `z= pm(sqrt(5)-1)`

Discussion

4204.	If 1-p is a root of the equation x^(2)+px+1-p=0, then its roots are
Answer» `0,-1` `-1,1` `0,1` `-1,2` Solution :`LHL = UNDERSET(xrarro^(-))(LIM)(x)/(ln(1+x)).[x]^(2)ln2=ln2` `RHL = underset(xrarr0^(+))(Lim)(ln(e^(x^(2))+2sqrt(x)))/(sqrt(x)((tansqrt(x))/(sqrt(x))))=underset(xrarr0^(+))(Lim)(lne^(x^(2))+ln(1+(2sqrt(x))/(e^(x^(2)))))/(sqrt(x))` `=underset(xrarr0^(+))(Lim)(x^(2))/(sqrt(x))+ln(1+(2sqrt(x))/(e^(x^(2))))/((2sqrt(x))/(e^(x^(2))))x(2)/(e^(x^(2)))=2impliesLHL ne RHL `

Discussion

4205.	Integrate the following functions : x^(2n-1).cosx^(n)
Answer» ANSWER :`(1)/(N)[x^(n)SINX^(n)+cosx^(n)]+C`

Discussion

4206.	If a plane meets the coordinate axes in A, B, C such that the centroid of the triangle ABC is the point (p,q, r) then the equation of the plane is
Answer» `x/p + y/q + z/r = 1` `x/p + y/q + z/r = 2` `x/p + y/q + z/r = 3 ` `px + QY + RZ = 3` ANSWER :C

Discussion

4207.	If alpha,beta,gamma are roots of x^3-5x+4=0 then the quadratic equation whose roots are alpha^(2015), beta^(2015) is
Answer» 12 13 169 144 Answer :D

Discussion

4208.	A and B are two independent witnesses in a case. The probability that A will speak truth is 3/5 and the probability that B will speak truth is 1/4. A and B agree in a certain statement. Find the probability that the statement is true.
Answer» ANSWER :`(1)/(3)`

Discussion

4209.	Binary operation * on R -{-1} defined by a ** b = (a)/(b+1) is
Answer» * is ASSOCIATIVE and COMMUTATIVE * is associative but not commutative * is NEITHER associative nor commutative * is commutative but not associative ANSWER :C

Discussion

4210.	Jennifer bought a box of Crunchy Grain cereal. The nutrition facts on the box state that a serving size of the cereal is 3/4 cup and provides 210 calories, 50 of which are calories from fat. In addition, each serving of the cereal provides 180 milligrams of potassium, which is 5% of thedaily allowance for adults. If p percent of an adult’s daily allowance of potassium is provided by x servings of Crunchy Grain cereal per day, which of the following expresses p in terms of x ?
Answer» p = 0.5x p = 5x `p=(0.05)^x` `p=(1.05)^x` Solution : It’s given that each serving of Crunchy Grain cereal provides 5% of an adult’s daily allowance of POTASSIUM, so x servings would provide x times 5%. The percentage of an adult’s daily allowance of potassium, p, is 5 times the number of servings, x. Therefore, the percentage of an adult’s daily allowance of POTASSIUMCAN be expressed as p = 5x. Choices A, C, and D are INCORRECT and may RESULT from incorrectly converting 5% to its decimal equivalent, which isn’t necessary since p is expressed as a percentage. Additionally, choices C and D are incorrect because the CONTEXT should be represented by a linear relationship, not by an exponential relationship.

Discussion

4211.	Evaluation of definite integrals by subsitiution and properties of its : For real function f,f(-x)=-f(x)and int_(0)^(1)f(x)dx=5then int_(-1)^(0)f(t)dt=.......
Answer» 10 5 0 `-5` ANSWER :D

Discussion

4212.	Let z_(1)" and "z_(2) be complex numbers such that z_(1)+ i(bar(z_2))=0" and "arg(bar(z_1)z_2)=(pi)/(3). Then arg(bar(z_1)) is
Answer» `(pi)/(3)` `pi` `(pi)/(2)` `(5PI)/(12)` ANSWER :D

Discussion

4213.	int(1)/((e^(x)+e^(-x))^(2))dx=.....
Answer» `-(1)/(2(e^(2X)+1))+C` `(1)/(2(e^(2x)+1))+c` `-(1)/(e^(2x)+1)+c` NONE of these Answer :A

Discussion

4214.	Find all the points of discontinuity of the function 'f' defined by : f(x)={{:(x+2", if "xlt1),(0",if"x=1),(x-2", if"xgt1):}
Answer» ANSWER :X = 1

Discussion

4215.	int(x^(4) - 1)/(x^(2)(x^(4) + x^(2)+1)^(1//2)) dx iseqal to
Answer» `sqrt((X^(4) + x^(2) + 1)/(x))+c` `(x^(2))/( sqrt(x^(4) + x^(2) + 1))+c` `x(x^(4) + x^(2) + 1)^(3//2) + c ` `(sqrt(x^(4) +x^(2) + 1))/( x )+c` SOLUTION :`int( x^(4) - 1)/( x^(2) (x^(4)+ x^(2) + 1)^(1//2)) dx= int( 2x^(4)+x^(2)- ( x^(4)+x^(2) +1))/( x^(2) sqrt(x^(4) + x^(2) + 1))dx = int ((x(4x^(3) + 2x))/(2 sqrt( x^(4) +x^(2)+ 1))-sqrt(x^(4)+x^(2) + 1))/(x^(2))dx ` `=int(d)/( dx) ((sqrt(x^(4) + x^(2) +1))/( x))dx = ( sqrt( x^(4)+x^(2)+1))/(x ) + c `

Discussion

4216.	Find the area of a loop as well as the whole area of the curvea^(2) y^(2) = x^(2)(a^(2) - x^(2)).
Answer» ANSWER :TOTAL AREA `=2xx2/3a^(2) = 4/3 a^(2) ` sq. units

Discussion

4217.	Jennifer bought a box of Crunchy Grain cereal. The nutrition facts on the box state that a serving size of the cereal is 3/4 cup and provides 210 calories, 50 of which are calories from fat. In addition, each serving of the cereal provides 180 milligrams of potassium, which is 5% of thedaily allowance for adults. On Tuesday, Jennifer will mix Crunchy Grain cereal with Super Grain cereal for her breakfast. Super Grain cereal provides 240 calories per cup. If the total number of calories in one cup of Jennifer’s mixture is 270, how much Super Grain cereal is in one cup of the mixture?
Answer» `1/8` cup `1/4` cup `1/3` cup `1/2` cup Solution : It’s given that a`3/4`- cup serving of Crunchy Grain cereal provides 210 calories. The total number of calories per cup can be found by dividing 210 by`3/4`, which gives ` 210div3/4= 280` calories per cup. LET c be the number of cups of Crunchy Grain cereal and s be the number of cups of Super Grain cereal. The expression 280c represents the number of calories in c cups of Crunchy Grain cereal, and 240s represents the number of calories in s cups of Super Grain cereal.The equation 280c + 240s = 270 gives the total number of calories in one cup of the mixture. Since c + s = 1 cup, c = 1 − s. Substituting 1 − s for c in the equation 280c + 240s = 270 yields 280(1 − s) + 240s = 270, or 280 − 280s + 240s = 270. Simplifying this equation yields280 − 40s = 270. Subtracting 280 from both sides results in −40s = −10. Dividing both sides of the equation by −40 results in `s =1/4`,so there is`1/4`cup of Super Grain cereal in one cup of the mixture. Choices A, C, and D are incorrect and may result from incorrectly creating or SOLVING the system of equations.

Discussion

4218.	The order and degree of the differential equation of all circles in the first quadrant which touch the co-ordinate axes is
Answer» 1,2 2,1 3,2 4,3 Answer :A

Discussion

4219.	Let R = {(a,a^3) \| ais a prime number less than 10} dom R.
Answer» Solution :R = {(a,a^3)\| a is a PRIME NUMBER less than 10 . dom R = {2,3,5,7}

Discussion

4220.	STATEMENT-1 : The lines from vertex to the two extremities of a focal chord of parabola y^(2) =4ax are at an angle pi//2. and STATEMENT-2 : If extremities of focal chord of parabola are (at_(1)^(""2), 2at_(1)) and (at_(2)^(""2), 2at_(2)) then t_(1)t_(2) = -1.
Answer» STATEMENT-1 is true, statement-2 is true, Statement -2 is a CORRECT explanation for Statement -1 Statement -1 is true, Statement-2 is true , Statement-2 is NOT a correct explanation for statement-1 Statement-1 is true, Statement-2 is False Statement-1 is False, Statement-2 is true ANSWER :D

Discussion

4221.	Find the equation of the circle which cuts orthogonally the circlex^2+y^2-4x+2y-7=0 and having the centre at (2,3)
Answer» ANSWER :`x^2+y^2-4x-6y+9=0`

Discussion

4222.	If int(e^(x))(1-sinx)/(1-cosx)dx=f(x) constant, then f(x) is equal to
Answer» `E^(X)COT(x/2) +C` `e^(-x)cot(x/2)+c` `-e^(x)cot(x/2)+c` `-e^(x) cot(x/2)+c` ANSWER :C

Discussion

4223.	If 9 fair dice are each thrown 4 times, then find the probability that the scores 1, 2, 3, 4, 5 and 6 each appear 6 times.
Answer» ANSWER :`(\|UL(36))/((\|ul(6))^(6) XX 6^(36))`

Discussion

4224.	Ifvec(a) = 2 hat (i) + 4 hat (j) - 3 hat (k) , vec (b) = hat (i) + mhat (k) and \|vec(a) xx vec (b)\| = 0 , then the values of m is -
Answer» `3/2` `-3` `-3/2` 3 Answer :C

Discussion

4225.	Compute the area of the figure bounded by the parabolas x= -2y^(2), x= 1-3y^(2)
Answer» ANSWER :`(4)/(3)`

Discussion

4226.	If f(x) = {{:(a+ (sin[x])/(x) ,"," x gt 0),(2,"," x=0 ),(b+[(sinx - x)/(x^3)],"," x gt 0):} , (where [.] denotes the greatest integer function).
Answer» SOLUTION :`f(0^+) =a ` as sin[x] = 0 as `x to 0` `f(0^-) = b-1 ` as `(SINX -x)/(x^3) = -(1)/6 + x/(4!) - (x^2)/(5!)+ …….` `f(0)=2 impliesa=2 , b=3`

Discussion

4227.	Let vec(a)=(1, -2, 3) and vec(b)=(3, 1, 2) be two vectors and vec(c)be a vector of length l and parallel to (vec(a)+vec(b)). What is vec(c) equal to ?
Answer» `(1)/(sqrt(4))(-2,-3,1)` `(1)/(sqrt(2))(1,0,1)` `(1)/(sqrt(42))(-5,-4,1)` None of these Solution :Given `vec(a)=vec(i)-2hat(J)+3hat(K)` and `vec(b)=3hat(i)+HAT(j)+2hat(k)` `:.vec(a)+vec(b)=4hat(i)-j+5hat(k)` Then, `vec(c)=lambda(vec(a)+vec(b))` `=lambda(4hat(i)-hat(j)+5hat(k))` `rArr L=sqrt(16lambda^(2)+lambda^(2)+25lambda^(2))` `l=sqrt(42)lambda` `lambda=(l)/(sqrt(42))` `:. vec(c)=(l)/(sqrt(42))(4hat(i)-hat(j)+5hat(k))=(1)/(sqrt(42))(4, -1, 5)`

Discussion

4228.	Evalute the following integrals int sin^(4) "x cos"^(5)xdx
Answer»

Discussion

4229.	Four bad eggs are accidentally mixed with 10 good ones. Three eggs are drawn simultaneously at random. Find the mean and variance of the bad eggs drawn.
Answer» ANSWER :MEAN `=(6)/(7)~~0.88` Variance=0.52`

Discussion

4230.	If C(x)=0.05x - 0.2x^(2) - 5 find the value of output for which the average cost becomes equal to the marginal cost.
Answer» ANSWER :x=5

Discussion

4231.	If E_1 ,E_2 and E_3 represent respectively the kinetic energies of an electron, an a-particle and a proton each having same de-Broglie's wavelength then
Answer» `E_1gtE_2gtE_3` `E_2gtE_3gtE_1` `E_1gtE_2gtE_2` `E_1=E_2=E_3` ANSWER :C

Discussion

4232.	If zbarz+(3-4i)z+(3+4i)barz=0 represent a circle, then area of the circle (in square units) is
Answer» `5PI` `10PI` `25pi^(2)` `25pi` ANSWER :D

Discussion

4233.	20 persons are sitting around a circle. In how many ways 7 persons out of them can be selected so that no two of the selected 7 are consecutive.
Answer» ANSWER :2640

Discussion

4234.	Integrate the following functions cosx/sqrt(1+sinx)
Answer» SOLUTION :LET t = 1+sinx. Then dt = COSX dx therefore` int cosx/sqrt(1+sinx) dx = int 1/sqrtt (dt)` `2sqrtt+c = 2sqrt(1+sinx+c)`

Discussion

4235.	Let Q_(0) be the set of all nonzero reational numbers Let * be a binary operation on Q_(0) defined by ab =(ab)/(4) for all a,b in Q_(0) (i) Show that is commutative and associative (ii) Find the identity element in Q_(0) (iii) Find the inverse of an element a in Q_(0)
Answer» Solution :(i) `forall a,b,c in Q_(0)` we have `ab=(AB)/(4)=(ba)/(4)=ba` And `(ab)C =(ab)/(4)c=((ab)/(4).c)/(4)=(ABV)c/(16)` Also `a(bc)=a(bc)/(4)=(a(bc)/(4))/(4)=a(bc)/(16)` But (ab) c = (bc) Hence (ab)c=a(bc) (ii) Let e be the identitiy elemn NAD let a in `Q_(0)`Then `Ae=a rarr (ae)/(4) rarr e=4` (iii) Let a in `Q_(0)` and let its inverse be b then `ab=e rarr (ab)/(4) rarrb=(16)/(a) in Q_(0)` Thus each a in `Q_(0) has (16)/(a)` as its inverse

Discussion

4236.	The positive integer just greater than (1 + .0001)^(10000) is
Answer» 4 5 2 3 Answer :C

Discussion

4237.	Two rods of legths a and b slide along coordinate axes. Such that their ends are concylic. Locus of the centre of the circle is
Answer» `4(X^(2)+y^(2))=a^(2)+b^(2)` `4(x^(2)+y^(2))=a^(2)-b^(2)` `4(x^(2)-y^(2))=a^(2)-b^(2)` `xy=ab` ANSWER :C

Discussion

4238.	cos12^(@)+cos84^(@)+cos132^(@)+cos156^(@)=
Answer» `1/2` `1/4` `-1/4` `-1/2` ANSWER :D

Discussion

4239.	If each base of a trapezoid is reduced by 50% and the highest of the trapezoid is quadrupled, how would the area of trapezoid change?
Answer» The AREA WOULD be MULTIPLIED by 4. The area would be multiplied by 2. The area would not change. The area would be CUT in half. Answer :B

Discussion

4240.	Charles Richter defined the magnitude of an earthquake to beM = log_(10) I/S, where I is the intensity of the earthquake (measured bythe amplitude of a seismograph reading taken 100 km from the epicentre of the earthquake) and S is the intensity of a ''standed earthquake'' (whose amplitude is 1 micron =10^(-1) cm). Each number increase on the Richter scale indicates an intensity ten times stronger. For example. an earthquake ofmagnitude 5. An earthquake of magnitude 7 is 100 times stronger then an earthquake of magnitude 5. An earthquake ofmagnitude 8 is 1000 times stronger than an earthquake of magnitude 5. The earthquake in city Aregistered 8.3 on the Richter scale. In the same year, another earthquake was recorded incity Bthat was four times stronger. What was the magnitude of the earthquake in city B ?
Answer» Solution :`M _(A) = log_(10). (I_(A))/S` `:.8.3 = log_(10). (I_(A))/S` Now`M_(B) = log_(10). (I_(B))/S` Where` I_(B) = 4I_(A)*` ` :.M_(B) = log_(10). (4I_(A))/S` ` = log_(10) 4+ log_(10). (I_(A))/S` ` = 0.6020 + 8.3` ` = 8.9020` So, magnitude of EARTHQUAKE in CITY B is ` 8.9020`.

Discussion

4241.	The ratio of the areas bounded by y=cosx,y=cos2x between x=0 and x=pi//3 and the x-axis is
Answer» `1:2` `2:1` `SQRT(3):4` `2sqrt(3):4-sqrt(3)` ANSWER :D

Discussion

4242.	Let a gt 1 " and "b gt 1. If f(t) is a periodic function of period T and int_(0)^(infty)a^(-bi)f(t)dt=kint_(0)^(T)a^(-bt)f(t)dt then k =
Answer» `a^(BT)/(T+1)` `a^(-bT)/(a^(-bT)+1)` `a^(bT)/(B^(aT)+1)` `a^(bT)/(a^(bT)-1)` ANSWER :D

Discussion

4243.	Find the real numbers (x,y) that satisfy the equation: xy^(2) = 15x^(2) +17xy + 15y^(2) x^(2)y = 20x^(2) + 3y^(2)
Answer» ANSWER :`(X,y) =(19,45) & (0,0)`

Discussion

4244.	The valueofsqrt(2) (cos15^@- sin15^@) isequal to
Answer» `sqrt(3) ` `sqrt(2)` `1` `2` ANSWER :C

Discussion

4245.	Find the area enclosed with in the curve x^(2)=4y,x=2, y=0
Answer» ANSWER :`(2)/(3)`

Discussion

4246.	The random variable X has a probability distribution P(X) of the following form, where K is some number P(X)={{:(,K,"if x =0"),(,2K,"if x=1 "),(,3K,"if x=2 "),(,0,"otherwise"):} (a) Determine the value of K. (b) Find P(X lt 2).
Answer» <P> Answer :(a) `k=(1)/(6)` (b)`P(X lt 2)=(1)/(2), P(X le 2)=1, P(X GE 2)=(1)/(2)`

Discussion

4247.	int[1/(Inx)-1/(Inx)^2]dx
Answer» Solution :`int[1/(Inx)-1/(Inx)^2]dx` =`int1/(Inx).1-INTDX/(Inx)^2` [INTEGRATING by parts taking `1/(Inx)` as first function and 1 as second function.] =`1/(Inx).x-int(-1)/(Inx)^2 . 1/x.xdx-intdx/(Inx)^2+C` =`x/(Inx)+intdx/(Inx)^2-intdx/(Inx)^2+C` `x/(Inx)+C`

Discussion

4248.	Matchthe following {:("System of lines", "Point of concurrence"), (I. (3k-1)x-(2k+3)y+(9-k)=0, (a)"(-2, 1)"),(II. (a+2b)x+(a-b)y+(a+5b)=0, (b)"(3, 4)"),(III. (2x+3y+1)+k(3x-2y-5)=0, (c)"(2, 2)"),(IV. a(x+y-4)+b(2x-y-2)=0, (d)"(1, -1)"):}
Answer» B, C, d , a b, a, d, c d, c, b, a a, b, c, d Answer :B

Discussion

4249.	Two samples of water of equal mass are heated to 60 degrees Celsius (°C). One sample is poured into an insulated container, and the other sample is poured into a non-insulated container. The samples are then left for 70 minutes to cool in a room having a temperature of 25°C. The graph above shows the temperature of each sample at 10-minute intervals. Which of the following statements correctly compares the average rates at which the temperatures of the two samples change?
Answer» In every 10-minute interval, the magnitude of the rate of change of TEMPERATURE of the insulated sample is greater than that of the non-insulated sample. In every 10-minute interval, the magnitude of the rate of change of temperature of the non-insulated sample is greater than that of the insulated sample. In the intervals from 0 to 10 minutes and from 10 to 20 minutes, the rates of change of temperature of the insulated sample are of greater magnitude, WHEREAS in the intervals from 40 to 50 minutes and from 50 to 60 minutes, the rates of change of temperature of the non-insulated sample are of greater magnitude. In the intervals from 0 to 10 minutes and from 10 to 20 minutes, the rates of change of temperature of the non-insulated sample are of greater magnitude, whereas in the intervals from 40 to 50 minutes and from 50 to 60 minutes, the rates of change of temperature of the insulated sample are of greater magnitude. Solution :Choice D is CORRECT. According to the graph, in the interval from 0 to 10 minutes, the non-insulated sample decreased in temperature by about 18°C, while the insulated sample decreased by about 8°C, in the interval from 10 to 20 minutes, the non-insulated sample decreased in temperature by about 9°C, while the insulated sample decreased by about 5°C, in the intervalfrom 40 to 50 minutes, the non-insulated sample decreased in temperature by about 1°C, while the insulated sample decreased by about 3°C, and in the interval from 50 to 60 minutes, the non-insulated sample decreased in temperature by about 1°C, while the insulated sample decreased by about 2°C. The description in choice D accurately summarizes these rates of temperature change over the given intervals. (Note that since the TWO samples of water have equal mass and so must lose the same amount of heat to cool from 60°C to 25°C, the faster cooling of the non-insulated sample at the start of the cooling process must be balanced out by faster cooling of the insulated sample at the end of the cooling process.) Choices A, B, and C are incorrect. None of these descriptions accurately compares the rates of temperature change shown in the graph for the 10-minute intervals.

Discussion

4250.	Drew the graph of y=cos^(-1)sqrt(log_([x])(\|x\|/x)) where [*] represents the greastest integer function.
Answer» SOLUTION :We have `y=f(x)=cos^(-1)sqrt(log_([x])(\|x\|/x))` `\|x\|/x={{:(1,xgt0),(-1,XLT0):}` We must have `xgt0` Also` [x]gt0" and "[x]ne1` `therefore""[x]GE2" or "xge2` From (i) and (ii), the domain of the function is `(2, oo)` For`xge2, \|x\|/x=1` `therefore""log_([x])(\|x\|/x)=0-(" for "xge2)` `therefore""sqrt(log_([x])(\|x\|/x))=0(" for "x ge 2)` `therefore""cos^(-1)sqrt(log_([x])(\|x\|/x))=pi/2` HENCE, GRAPH of `y=f(x)" if the line y"=pi/2" for "x in [2, oo)`.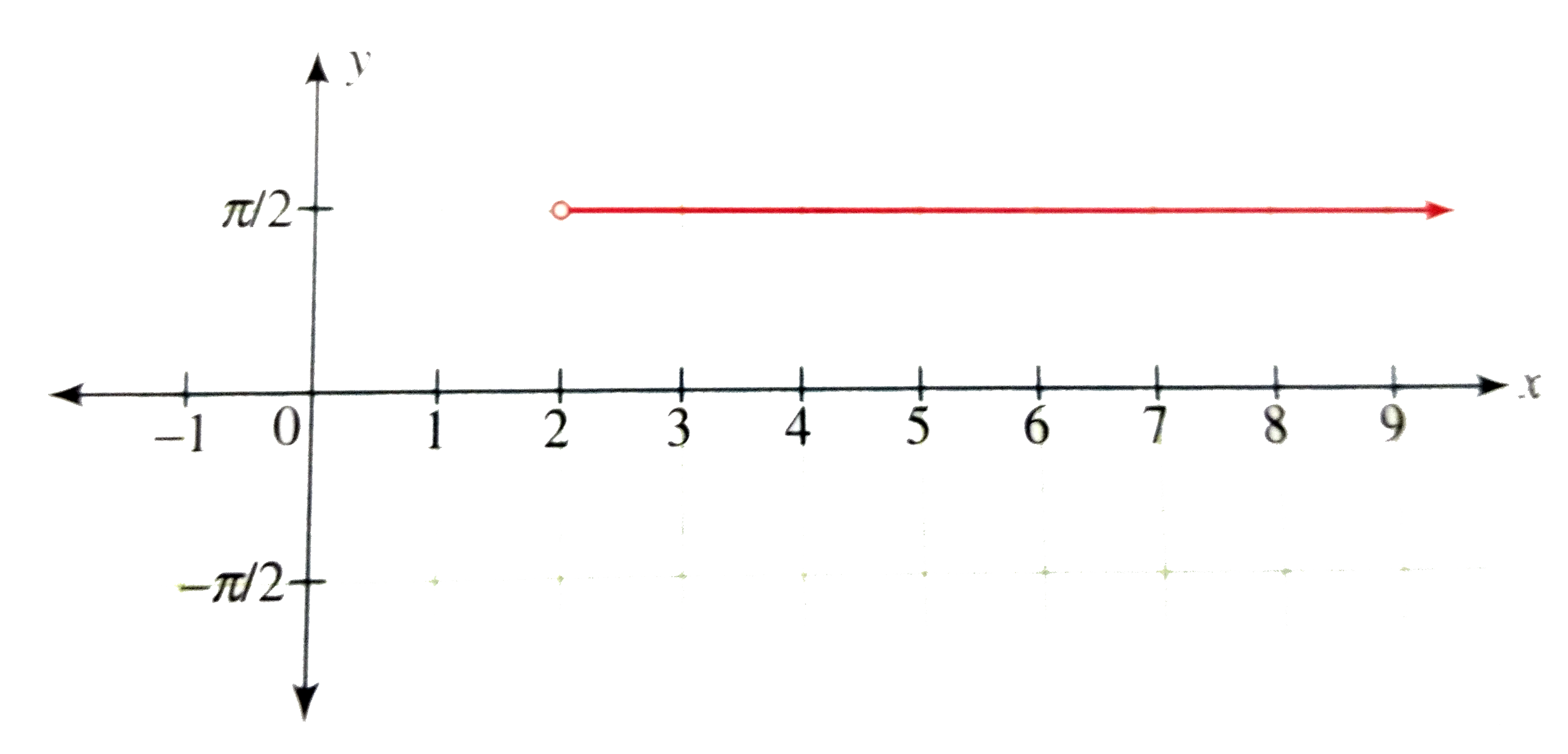

Discussion

Explore topic-wise InterviewSolutions in .

A positive divisor of 1800 is selected at random and given that the selected divisor is a multiple of 10. Find the probability that it is a multiple of 25.

Evalute the following integrals int sqrt(1 + 3x - x^(2)) dx

Complex numbers z satisfy the equaiton |z-(4//z)|=2 Locus of z if |z-z_(1)| = |z-z_(2)|, where z_(1)and z_(2) are complex numbers withthe greatest and the least moduli, is

If 1-p is a root of the equation x^(2)+px+1-p=0, then its roots are

Integrate the following functions : x^(2n-1).cosx^(n)

If a plane meets the coordinate axes in A, B, C such that the centroid of the triangle ABC is the point (p,q, r) then the equation of the plane is

If alpha,beta,gamma are roots of x^3-5x+4=0 then the quadratic equation whose roots are alpha^(2015), beta^(2015) is

A and B are two independent witnesses in a case. The probability that A will speak truth is 3/5 and the probability that B will speak truth is 1/4. A and B agree in a certain statement. Find the probability that the statement is true.

Binary operation * on R -{-1} defined by a ** b = (a)/(b+1) is

Evaluation of definite integrals by subsitiution and properties of its : For real function f,f(-x)=-f(x)and int_(0)^(1)f(x)dx=5then int_(-1)^(0)f(t)dt=.......

Let z_(1)" and "z_(2) be complex numbers such that z_(1)+ i(bar(z_2))=0" and "arg(bar(z_1)z_2)=(pi)/(3). Then arg(bar(z_1)) is

int(1)/((e^(x)+e^(-x))^(2))dx=.....

Find all the points of discontinuity of the function 'f' defined by : f(x)={{:(x+2", if "xlt1),(0",if"x=1),(x-2", if"xgt1):}

int(x^(4) - 1)/(x^(2)(x^(4) + x^(2)+1)^(1//2)) dx iseqal to

Find the area of a loop as well as the whole area of the curvea^(2) y^(2) = x^(2)(a^(2) - x^(2)).

The order and degree of the differential equation of all circles in the first quadrant which touch the co-ordinate axes is

Let R = {(a,a^3) | ais a prime number less than 10} dom R.

STATEMENT-1 : The lines from vertex to the two extremities of a focal chord of parabola y^(2) =4ax are at an angle pi//2. and STATEMENT-2 : If extremities of focal chord of parabola are (at_(1)^(""2), 2at_(1)) and (at_(2)^(""2), 2at_(2)) then t_(1)t_(2) = -1.

Find the equation of the circle which cuts orthogonally the circlex^2+y^2-4x+2y-7=0 and having the centre at (2,3)

If int(e^(x))(1-sinx)/(1-cosx)dx=f(x) constant, then f(x) is equal to

If 9 fair dice are each thrown 4 times, then find the probability that the scores 1, 2, 3, 4, 5 and 6 each appear 6 times.

Ifvec(a) = 2 hat (i) + 4 hat (j) - 3 hat (k) , vec (b) = hat (i) + mhat (k) and |vec(a) xx vec (b)| = 0 , then the values of m is -

Compute the area of the figure bounded by the parabolas x= -2y^(2), x= 1-3y^(2)

If f(x) = {{:(a+ (sin[x])/(x) ,"," x gt 0),(2,"," x=0 ),(b+[(sinx - x)/(x^3)],"," x gt 0):} , (where [.] denotes the greatest integer function).

Let vec(a)=(1, -2, 3) and vec(b)=(3, 1, 2) be two vectors and vec(c)be a vector of length l and parallel to (vec(a)+vec(b)). What is vec(c) equal to ?

Evalute the following integrals int sin^(4) "x cos"^(5)xdx

Four bad eggs are accidentally mixed with 10 good ones. Three eggs are drawn simultaneously at random. Find the mean and variance of the bad eggs drawn.

If C(x)=0.05x - 0.2x^(2) - 5 find the value of output for which the average cost becomes equal to the marginal cost.

If E_1 ,E_2 and E_3 represent respectively the kinetic energies of an electron, an a-particle and a proton each having same de-Broglie's wavelength then

If zbarz+(3-4i)z+(3+4i)barz=0 represent a circle, then area of the circle (in square units) is

20 persons are sitting around a circle. In how many ways 7 persons out of them can be selected so that no two of the selected 7 are consecutive.

Integrate the following functions cosx/sqrt(1+sinx)

Let Q_(0) be the set of all nonzero reational numbers Let * be a binary operation on Q_(0) defined by a*b =(ab)/(4) for all a,b in Q_(0) (i) Show that * is commutative and associative (ii) Find the identity element in Q_(0) (iii) Find the inverse of an element a in Q_(0)

The positive integer just greater than (1 + .0001)^(10000) is

Two rods of legths a and b slide along coordinate axes. Such that their ends are concylic. Locus of the centre of the circle is

cos12^(@)+cos84^(@)+cos132^(@)+cos156^(@)=

If each base of a trapezoid is reduced by 50% and the highest of the trapezoid is quadrupled, how would the area of trapezoid change?

The ratio of the areas bounded by y=cosx,y=cos2x between x=0 and x=pi//3 and the x-axis is

Let a gt 1 " and "b gt 1. If f(t) is a periodic function of period T and int_(0)^(infty)a^(-bi)f(t)dt=kint_(0)^(T)a^(-bt)f(t)dt then k =

Find the real numbers (x,y) that satisfy the equation: xy^(2) = 15x^(2) +17xy + 15y^(2) x^(2)y = 20x^(2) + 3y^(2)

The valueofsqrt(2) (cos15^@- sin15^@) isequal to

Find the area enclosed with in the curve x^(2)=4y,x=2, y=0

The random variable X has a probability distribution P(X) of the following form, where K is some number P(X)={{:(,K,"if x =0"),(,2K,"if x=1 "),(,3K,"if x=2 "),(,0,"otherwise"):} (a) Determine the value of K. (b) Find P(X lt 2).

int[1/(Inx)-1/(Inx)^2]dx

Matchthe following {:("System of lines", "Point of concurrence"), (I. (3k-1)x-(2k+3)y+(9-k)=0, (a)"(-2, 1)"),(II. (a+2b)x+(a-b)y+(a+5b)=0, (b)"(3, 4)"),(III. (2x+3y+1)+k(3x-2y-5)=0, (c)"(2, 2)"),(IV. a(x+y-4)+b(2x-y-2)=0, (d)"(1, -1)"):}

Drew the graph of y=cos^(-1)sqrt(log_([x])(|x|/x)) where [*] represents the greastest integer function.

Let Q_(0) be the set of all nonzero reational numbers Let * be a binary operation on Q_(0) defined by ab =(ab)/(4) for all a,b in Q_(0) (i) Show that is commutative and associative (ii) Find the identity element in Q_(0) (iii) Find the inverse of an element a in Q_(0)