InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 4101. |
Let A, B, C be three points on bar(OX),bar(OY),bar(OZ)respectively at the distances 3, 6, 9 from origin. Let Q be the point (2, 5, 8) and P be the pointequidistant from O,A,B,C.Them,thecoordinates of the point R which divides PQ in the ratio : 2 is |
|
Answer» `((17)/(10),(29)/(5),(43)/(10))` |
|
| 4102. |
If A={1,2,3,4}B={1,2,3,4,5,6} and f :A to B is an injective mapping satisfying f (i) ne I, then number of such mappings are : |
|
Answer» 182 |
|
| 4103. |
A die is thrown twice and the sum of the numbers appearing is observed to be 6. What is the conditional probability that the number 4 has appeared at least once? |
|
Answer» |
|
| 4104. |
If vec(z_(1)) = a hat(i) + b hat(j) and vec(z_(2)) = c hat(i) + d hat(j)are two vectors in hat(i) and hat(j) system where |vec(z_(1))| = |vec(z_(2))| = rand vec(z_(1)).vec(z_(2)) = 0then vec(w_(1)) = ahat(i) + chat(j) and vec(w_(2)) = b hat(i) + d hat(j) satisfy . |
|
Answer» `|vec(w_(1))| = R` |
|
| 4105. |
If A=[{:(1,2,3),(2,3,1):}]andB=[{:(3,-1,3),(-1,0,2):}], then find 2A-B. |
|
Answer» |
|
| 4106. |
Let n(U) = 700 , n (A) = 200 , n (B) = 300 and n (A nn B) =100, then n(A' nn B')= |
|
Answer» 90 |
|
| 4107. |
If z_1 andz_2are two non- zero comlex numbers such that |z_1+z_2|=|z_1|+|z_2| then arg (z_1)- arg (z_2) is equal to |
|
Answer» `-pi` On squaring both SIDES ,we GET `|z_1|^2 + |Z_2|^2+2|z_1||z_2|cos (ARG z_1 - arg z_2)=|z_1|^2|z_2|^2+2|z_1||z_2|` ` rArr2|z_1||z_2|cos (arg z_1-arg z_2)=2|z_1|z_2|` `rArrcos(arg z_1 - arg z_2)=1` `rArrarg(z_1)aargz_2)=0` |
|
| 4108. |
Integrate the function is Exercise. cos^(3)x e^(log sinx) |
|
Answer» |
|
| 4109. |
Let A,B,C be angles of triangles with vertex A -= (4,-1) and internal angular bisectors of angles B and C be x - 1 = 0 and x - y - 1 = 0 respectively. Slope of BC is |
|
Answer» `1//2` 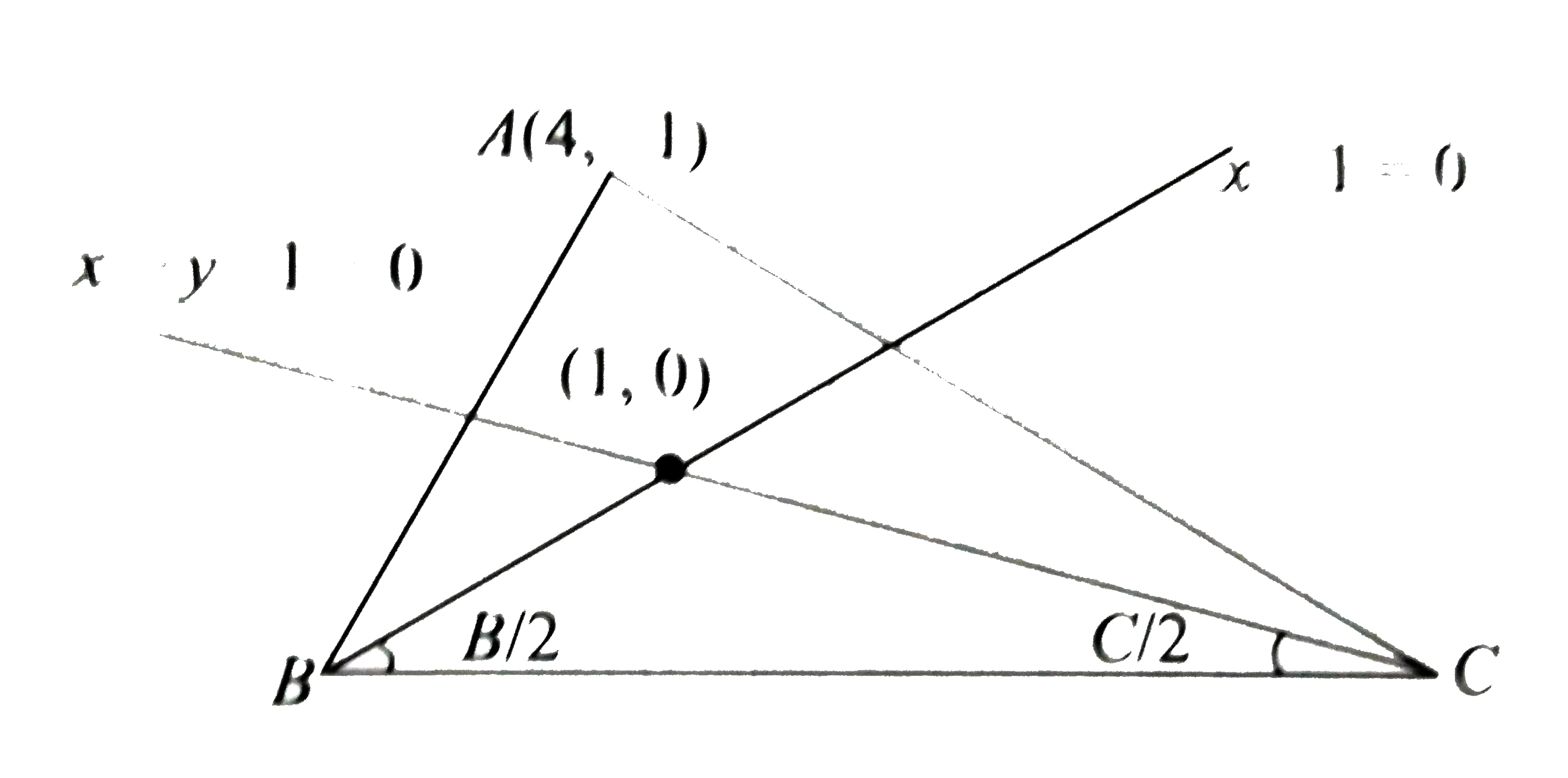 Image of `A(4,-1)` in bisectors of B and C lies on SIDE BC `rArr` Image of `A(4,-1)` with respect to `x-y -1 =0` is `(x-4)/(1) =(y+1)/(-1) =-(2(4+1-1))/(2) rArr (0,3)` Image of `A(4,-1)` with respect to `x -1 =0` is `(x-4)/(1) =(y+1)/(0) =- (2(4-1))/(1) rArr (-2,-1)` Hence, SLOPE of BC is `m = ((3+1)/(0+2)) =2` |
|
| 4110. |
Let A,B,C be angles of triangles with vertex A -= (4,-1) and internal angular bisectors of angles B and C be x - 1 = 0 and x - y - 1 = 0 respectively. If A,B,C are angles of triangle at vertices A,B,C respectively then cot ((B)/(2))cot .((C)/(2)) = |
|
Answer» 2 Angle between `x -y -1 =0` and BC is `(C )/(2) rArr tan.(C )/(2) =(1)/(3)` `rArr cot.(B)/(2) cot.(C )/(2) =6` |
|
| 4111. |
Let S = Set of all women in the world. Define R as follows: a, b in S, a Rb if a and b have at least one of the two parents in common, Then |
|
Answer» R is REFLEXIVE and SYMMETRIC only |
|
| 4112. |
A student has obtained 75%, 80% and 855 in three subjects. If the marks of another subject are added then his average can not be less than |
|
Answer» 0.6 |
|
| 4113. |
8-digit numbers are formed using the digits 1,1,2,2,2,3,4,4. Thenumber of such numbers in which the odd digits do not occupy odd places, is |
|
Answer» 160 |
|
| 4114. |
Express as a sum of a symmetric and a skew symmetric matrix:[[0,1],[1,0]] |
|
Answer» SOLUTION :`LET A=[[0,1],[1,0]]` `impliesA=[[0,1],[1,0]]=A` `:.`A is SYMMETRIC. Now A=A+0 where A is symmetric and O is SKEW symmetric. |
|
| 4115. |
Find intervals in which the function given by f(x)=(3)/(10)x^(4)-(4)/(5)x^(3)-3x^(2)+(36)/(5)x+11is (a) Increasing (b) Decreasing. |
|
Answer» Strickly DECREASES `(-oo, -2), (1,3)` |
|
| 4116. |
Given two independent events A and B such that P(A)= 0.3, P(B)= 0.6. FindP(A or B) |
|
Answer» |
|
| 4117. |
A house has an old gas furnace that is only 70% efficient . This means that only 70% of the heat produced by the gas goes into heating the house , while 30% of the least is lost . There is a constant charge per unit of gas , and the owner's gas bill is $1,200 per year . The owner is considering replacing the furnace witha new one that is 90 percent energy efficient . To the nearest dollar ,what would the gas bill be per year, assuming that the same amount of heat is required for the house ? |
|
Answer» 896 |
|
| 4118. |
A house has an old gas furnace that is only 70% efficient . This means that only 70% of the heat produced by the gas goes into heating the house , while 30% of the least is lost . There is a constant charge per unit of gas , and the owner's gas bill is $1,200 per year . Instead of replacing the furnace , the owner keeps the old furnace but doubles the thicknessof insulation under the roof , thus cutting the heat loss by a factor of two . Assume that most of the heat supplied by the furnace goes into replacing the heat lost through the roof .If it costs $2,000 to install the insulation, how many years is the payback period , namely , after how many years would the cost of insulation equalthe savings on the gas bill ? Round your answer to the nearest tenth. |
|
Answer» 2.7 |
|
| 4119. |
Evaluate lim_(n to oo) sum_(i=1)^(n)(1)/(n) [(n-i)/(n+i)] by using the method of finding definite integral as thelimit of a sum. |
|
Answer» |
|
| 4120. |
A family of curves has the differential equation xy(dy)/(dx)=2y^(2)-x^(2). Then, the family of curves is |
|
Answer» `y^(2) = x + C x^(4)` |
|
| 4121. |
If f(x) is continuous atx=0, where f(x)=(sin(x^(2)-x))/(x), for x!=0, then f(0)= |
|
Answer» -1 |
|
| 4122. |
If (alpha, beta) are the roots of the equation 15 x ^(2) - 22 x + 8=0 and (alpha', beta') are the roots of the equation 8x^(2) - 22x + 15=0, then the equation of the circle on A (alpha, alpha') and B (beta, beta') as diameter is |
|
Answer» `120 (x ^(2) + y ^(2)) - 22 ( 8X + 15y) + 289 =0` |
|
| 4123. |
Show that y = (cos^(-1) x)^(2)is a solution of the differential equation . (1-x^(2))y '' - xy' - 2 = 0 |
|
Answer» |
|
| 4124. |
C_0 + (C_1)/(2) (4) + (C_2)/(3) (16) + …………..+(C_n)/(n + 1) (2^(2n)) |
|
Answer» `(5^(N+1) + 1)/(n-1)` |
|
| 4125. |
Determine the unknown coordinates of the S(7,y,z) in x-"axis" |
| Answer» SOLUTION :y=0,z=0, | |
| 4126. |
If f(x)=|{:(cosx,1,0),(1,2cosx,1),(0,1,2cosx):}|" then "int_(0)^(pi//2)f(x)dx= |
|
Answer» `1/2` |
|
| 4127. |
Find the area of the smaller part of the circle x^(2) + y^(2) = a^(2) cut off by the line x = (a)/(sqrt(2)). |
|
Answer» |
|
| 4128. |
If x ge 0, y ge 0, 2x+y ge 0, x+2y ge 10, x+y le 10, then the minimum value of f=x-y is |
|
Answer» 5 |
|
| 4129. |
Write the following function in the simplest form : "tan"^(-1)(sqrt(1+x^(2))-1)/x, x!=0 |
|
Answer» ` |
|
| 4130. |
Find the area of the parallelogram whose adjacent sides are determined by the vectors veca=hati-hatj+3hatkandvecb=2veci-7hatj+hatk. |
|
Answer» |
|
| 4131. |
The sum of the numbers formed by taking all the digits at a time from 0, 2, 3, 4 is |
|
Answer» 57996 |
|
| 4132. |
54/7 pi radians is approximately equal to how many degrees? |
|
Answer» `8^@` |
|
| 4133. |
underset( x to oo)("lim") [(x^(2) + x + 3)/(x^(2) - x + 2)]^(x) is equal to |
| Answer» ANSWER :d | |
| 4134. |
Find the volume of the following parallelo-piped whose the coterminous edges are:veca=3overset^^i+4overset^^j,vecb=2overset^^i+3overset^^j+4overset^^k,vecc=5overset^^k |
|
Answer» SOLUTION :`=|(3,4,0),(2,3,4),(0,0,5)|` `5(9-8)=5"UNIT"^3` |
|
| 4135. |
ABCD is a rectangular park with AB = a. A tower standing at C makes angles alpha and beta at A and B respectively, the height of the tower is |
|
Answer» `(a)/(SQRT(cot^(2)ALPHA+cot^(2)beta))` |
|
| 4136. |
A company manufactures two types of toys A and B. Type A requires 5 minutes each for cutting and 10 minutes each for assembling. Type B requires 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours available for cutting and 4 hours available for assembling in a day. He earns a profit of Rs.50 each on type A and Rs.60 each on type. B. How many toys of each type should the company manufacture in a day to maximize the profit ? |
|
Answer» `5x+8yle180,` `5x+4yge120,` `x ge 0and YGE0.` The corner points of the feasible region are `O(0,0),C(24,0),D(0,22.5)and E(12,15).` z is MAXIMUM at `E(12,15).` |
|
| 4137. |
Find a unit vector parallel to the vector veca+vecb where veca=3hati+2hatj+2hatk and vecb=hati+2hatj-2hatk. |
| Answer» | |
| 4138. |
8 coins are tossed simultaneously. Find the probability of getting at least 6 heads. |
|
Answer» |
|
| 4139. |
C_0C_2 + C_1C_3 +C_2C_4+……..+C_(n-2) C_n = |
|
Answer» `""^(2N)C_(n-2)` |
|
| 4140. |
If (1)/(2)(z-4)(z+4)=m, then,in term of z, what is the value of z^(2)-16? |
| Answer» ANSWER :D | |
| 4141. |
If Delta=|(1+y,1-y,1-y),(1-y,1+y,1-y),(1-y,1-y,1+y)|=0, then value of y are |
|
Answer» 0,3 |
|
| 4142. |
If three numbers are drawn at random successively without replacement from a set S={1,2,…..10}, then the probability that the minimum of the chosennumbers is 3 or their maximum is 7 is |
|
Answer» `(1)/(40)` |
|
| 4143. |
Let alpha,beta,gamma be the roots of x^(3)+x+10=0 and alpha_(1)=(alpha+beta)/(gamma^(2)),beta_(1)=(beta+gamma)/(alpha^(2)),gamma_(1)=(gamma+alpha)/(beta^(2)). Then, the value of (alpha_(1)^(3)+beta_(1)^(3)+gamma_(1)^(3))-(1)/(10)(alpha_(1)^(2)+beta_(1)^(2)+gamma_(1)^(2)) is |
|
Answer» `(1)/(10)` |
|
| 4144. |
Which of the following is a homogenous differential equation ? |
|
Answer» `(4x+6y+5)dy-(3y+2x+4)dx=0` `(dy)/(dx)=(3y+2x+4)/(4x+6y+5)IMPLIES(dy)/(dx)=(x(3*(y)/(x)+2+(4)/(x))/(x(4+6(y)/(x)+(5)/(x))` whichis non-homogenous differential equation. `(b)` Given differential equation `xydx-(x^(3)+y^(3))dy=0` from the separating of VARIABLES, `(x^(3)+y^(3))dy=xydximplies(dy)/(dx)=(xy)/(x^(3)+y^(3))` `implies (dy)/(dx)=((y)/(x^(2)))/(1+((y)/(x))^(3))` which is non-homogenous differential equation `(c )` Given differential EQAUTION `(x^(3)+2y^(2))dx+2 xy dy=0` `2xy dy=-(x^(3)+2y^(2))dx` From the separating of variables, `(dy)/(dx)=-(x^(3)+2y^(2))/(2xy)implies(dy)/(dx)=(1+(2y^(2))/(x^(3)))/((2y)/(x^(2)))` which is non-homogenous differential equation. `(d)` Given differential equation `y^(2)dx+(x^(2)-xy-y^(2))dy=0` From the separating of variables, `(x^(2)-xy-y^(2))dy=-y^(2)dx` `implies (dy)/(dx)=-(y^(2))/(x^(2)-xy-y^(2))` `implies (dy)/(dx)=-(((y)/(x))^(2))/([1-(y)/(x)-((y)/(x))^(2)])` which is a homogenous differential equation. |
|
| 4145. |
Two balls , projected at different times so they don't collide, have trajectories A and B , as shown below . Which statement is correct ? |
|
Answer» If `v_(0A)` and `v_(0B)` are initial speeds of A & B respectively then `v_(0B)` must be greater then `v_(0A)`. |
|
| 4146. |
If f(x) = (log x)/(x^(3)) = then its antiderivative F(x) given by |
|
Answer» `C - (1)/(2x^(2)) log (xsqrt E)` |
|
| 4148. |
int(dx)/(x^(2)+2x+2)= |
|
Answer» `XTAN^(-1)(x+1)+C` |
|
| 4149. |
Find the distance between the parallel planes x + y - z + 4 = 0 and x + y - z + 5 = 0. |
|
Answer» |
|
| 4150. |
intsin^3xsec^14xdx |
|
Answer» SOLUTION :`intsin^3xsec^14xdx` =`intsin^3x/cos^14x dx` =`int((1-cos^2x)sinx)/cos^14x dx` [PUT cosx=t Then sinxdx=-DT] =`int(t^2-1)/t^14 dt=int(t^-12-t^-14)dt` =`-1/11t^-11+1/13t^-13+C` =`1/13sec^13x-1/11sec^11x+C` |
|