Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 51. |
x^(3) + 3x^(2) + 3x + 2 = (x+2) (………) |
|
Answer» `X-2` |
|
| 52. |
Use the Factor Theorem to determine whether g (x) is factor of f(x) in each of the following cases: (i) f (x) = 5x ^(3) + x ^(2)-5x -1, g (x)=x +1 (ii) f (x) = x ^(3) + 3x ^(2) + 3x +1 , g(x) =x +1 (iii) f (x) =x ^(3) - 4x ^(2) +x + 6, g (x) =x -2 (iv) f (x) = 3x ^(3) + x^(2) - 20x + 12, g (x) = 3x -2 (v)f (x) = 4x ^(3) + 20 x ^(2) + 33 x +18, g (x) =2x +3 |
|
Answer» |
|
| 53. |
A conical tent is 10 m high and the radius of its base is 24 m. Find (i) slant height of the tent. (ii) Cost of the canvas required to make the tent, if the cost of 1 m^(2) canvas is Rs. 70 |
|
Answer» (II) RS. 1,37,280 |
|
| 54. |
The mean of 15 observations is 32. Find the resulting mean, if each observation is multiplied by 2 |
|
Answer» |
|
| 55. |
Find the mean, the median and the mode of the observations 24, 12, 15, 28, 15, 22, 17. |
|
Answer» |
|
| 56. |
Amar, Bhavan and Chetan can make a total of 8 dosas in one minutes. They have to make a total of 80 days. Amar started making dosas After some time, Bhavan anc Chetan took over and completedthe job and Amar made atleast 5 doss per minutes, how long did Amar work alone (in minutes)? |
|
Answer» 9 (ii)A or B or C can make `(8)/(3)` dosas in one minute (iii) LET A alone WORK for x MINUTES , and B and C work fo (20-x) minutes each. (IV) `(8)/(3)xx x+(20-x)(8)/(3)+(20-x)(8)/(3)=80` |
|
| 57. |
A dia is thrown 1000 times with the following frequencies for outcomes 1, 2, 3, 4, 5 and 6 as given below: |{:("Outcome",1,2,3,4,5,6),("Frequency",179,150,157,149,175,190):}| Find the probability of happening of each outcome. |
|
Answer» |
|
| 59. |
Each side of an equilateral triangle measures 8 cm. Then, the semiperimeter of the triangle is ……………… cm. |
|
Answer» 4 |
|
| 60. |
The total surface area of a cuboid with length 20 cm, breadth 15 cm and height 10 cm is ……… cm^(2). |
|
Answer» 1300 |
|
| 61. |
P and Q are respectivelythe mid-pointsof sidesAB and BCof a triangleABCand Ris themid pointat AP, show that(i) ar (PQR) =1/2ar (ARC) (ii) ar (RQC) = 3/8ar (ABC) (iii) ar (PBQ) = ar (ARC) |
|
Answer» |
|
| 63. |
Awall of length 10 m was to be built across an open ground. The heightofthe wall is 4 m and thickness of the wall is 24 cm. If this wall is to bebuilt up with bricks whose dimensions are 24\ c m\ xx\ 12\ c m\ xx\ 8\ c m, how |
|
Answer» |
|
| 64. |
Construct a parallelogram PQRS with PR=3 cm , QS=4.2 cm, and the angle between the diagonals are equal to 75^(@), |
|
Answer» Solution :Step 1: Draw the diagonal PR=3 cm. Step 2: Bisect PR to mark the mid-point as O. Step 3: Construct an ANGLE of `75^(@)` at O, such that `anglePOX=75^(@)`. Step 4: Taking O as the CENTER and radius `=1/2(QS) =1/2 xx 4.2 =2.1`cm, draw arcson the angular line constructed in Step 3 to cut at Q and S. Step 5: JOIN PQ, QR, RS and SP to obtain the required parallelogram PQRS. 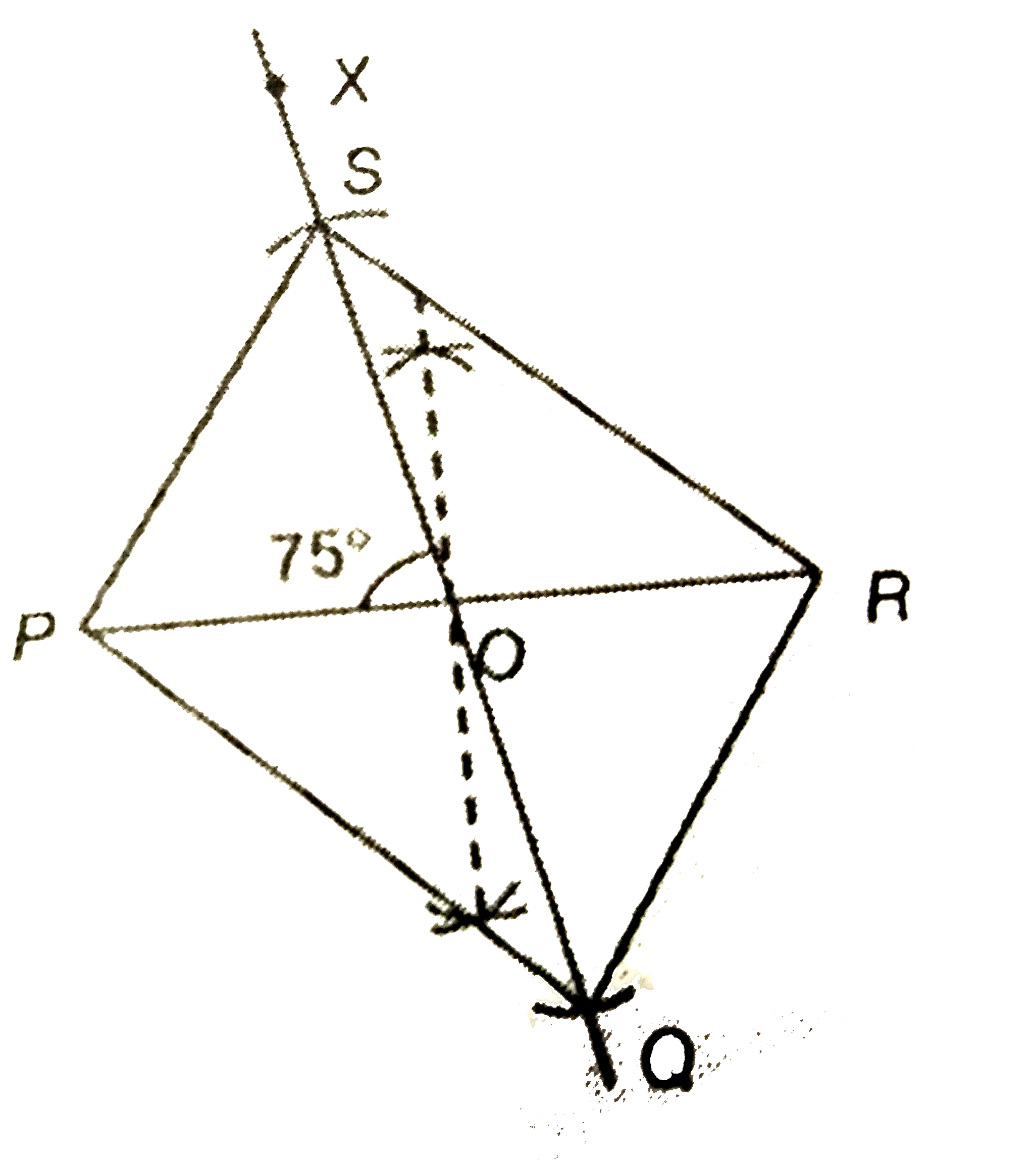
|
|
| 65. |
If in a computer language + means subtraction - means additon X means division / means multplication Then evalute the expression (1000+89)/(11-365xx5) as the compute perform when written that language |
|
Answer» 94 |
|
| 66. |
Simplify each of the following by rationalising the denominator: (6-4sqrt2)/(6+4sqrt2) |
|
Answer» |
|
| 67. |
From the given figure, find : Use tanx^(@), to find the value of y. |
|
Answer» |
|
| 68. |
On one page of a telephone directory, there were 200telephone numbers. The frequency distribution of their unit place digit (forexample, in the number 25828573, the unit place digit is 3) is given in Table:D igi t0 1 2 3 4 5 6 7 8 9F r e q u e |
|
Answer» |
|
| 69. |
Draw the graph for each equation given below: (i) x=4,(ii) x-6=0,(iii) x+3=0,(iv)y=2 ,(v) 2x-5=0, (vi) y+3=0 |
| Answer» | |
| 70. |
If the pointsA(4,6) and B(1,3) lie on thegraph of ax +by =8 then find thevalue ofa and b |
|
Answer» |
|
| 71. |
Factorise : x^(3) + 13x^(2) + 32x + 20 |
|
Answer» |
|
| 72. |
Consider the frequency distribution tabe (Table 3, sum no . 4 of ''Sums to Enrich 'Remember''' Chapter 14) , which gives the weights of 38 students of class. Give two events in this context, one having probability 0 and the other having probability 1. |
|
Answer» |
|
| 73. |
The distributionbelow gives the weights of 30 studentsof a class. Find the medianweightof the students : {:("Weight (in kg) ",40-45,45-50,50-55,55-60,60-65,65-70,70-75),("Number of students ",""2,""3,""8,""6,""6,""3,""2):} |
|
Answer» |
|
| 74. |
Construct a grouped frequency distribution table with width 10 of each class, in such a way that one of the class is 10-20 (20 not included). |
|
Answer» Solution :We arrange the given data into groups LIKE 0-10, 10-20, 20-30, ………… in which UPPER class LIMIT is not included in that class. The class width in each case is 10. The FREQUENCY distribution of the given data is given below 
|
|
| 75. |
In the given figure KLMN is a cyclic quadrilateral. KD is the tangent at K. If angleN is a diametar angleNLK=40^(@) and angleLNM=50^(@). Find angleMLN and angleDKL. |
|
Answer» |
|
| 76. |
If roots of the |
|
Answer» `2b^(-1)= a^(-1) + c^(-1)` (ii) If the sum of coefficient is 0, then 1 and `c/a` are the ROOTS of the equation. (III) Use productof the roots concept. |
|
| 78. |
Represent sqrt(5),sqrt(6),sqrt(7)andsqrt(11) on the number line. |
| Answer» SOLUTION :N/a | |
| 79. |
AD and BC are equal perpendiculars to a line segment AB (see the given figure) Show that CD bisects AB. |
|
Answer» |
|
| 81. |
The monthly electricity bill raised by themunicipal corporation consists of two parts-a fixed charge for providing the service and a variable charge which is directly proportional to the number of watts of powerconsumed. An amount of Rs. 500 is charged for consuming 125 watts in a particular month . The of 500 watts is 21 : 25 . How much is the fixedcharge per month? |
|
Answer» Rs. 125 (ii) Given data can be expressed asx + 100y. ` = 300.(x+300y)/(x +400y) = 5/6`. (iii) SOLVE the above TWO EQUATIONS and GET the value of x. |
|
| 82. |
If the mean of the following data is 7.5, then find the value of 'A'. |
|
Answer» 15 |
|
| 83. |
Verify whether the following are zeroes of the polynomial, indicated against them : p(x) = 3x^(2) -1, x = -(1)/(sqrt(3)), (2)/(sqrt(3)) |
|
Answer» |
|
| 84. |
Factorise : x^(3) - 4x^(2) - 7x + 10 |
|
Answer» |
|
| 85. |
State whether the following statements are true or false? Also give reasons for your answers. a) Only one line can pass through a given point. b) All right angles are equal. c) Circles with same radii are equal. d) A line segment can be extended on its both sides endlessly to get a straight line. e) From the figure, AB gt AC. |
|
Answer» |
|
| 86. |
Represent the data in the adjacent bar graph as frequency distribution table. |
|
Answer» |
|
| 87. |
If the mean of 2x, 5, 3x, 12, 5x, 17 and6 is 20, then x = .......... |
|
Answer» 10 |
|
| 89. |
Construct a DeltaABC in which AB = 5 cm, AC = 4.5 cm and angleA = 60^(@). |
|
Answer» Solution :STEPS of construction : 1. DRAW `AB = 5 cm.` 2. Draw `anglePAB =60^(@)` 3. Cut`AC = 4.5 cm` from `AP.` 4. Join `BC`. `therefore DeltaABC` is the required triangle. 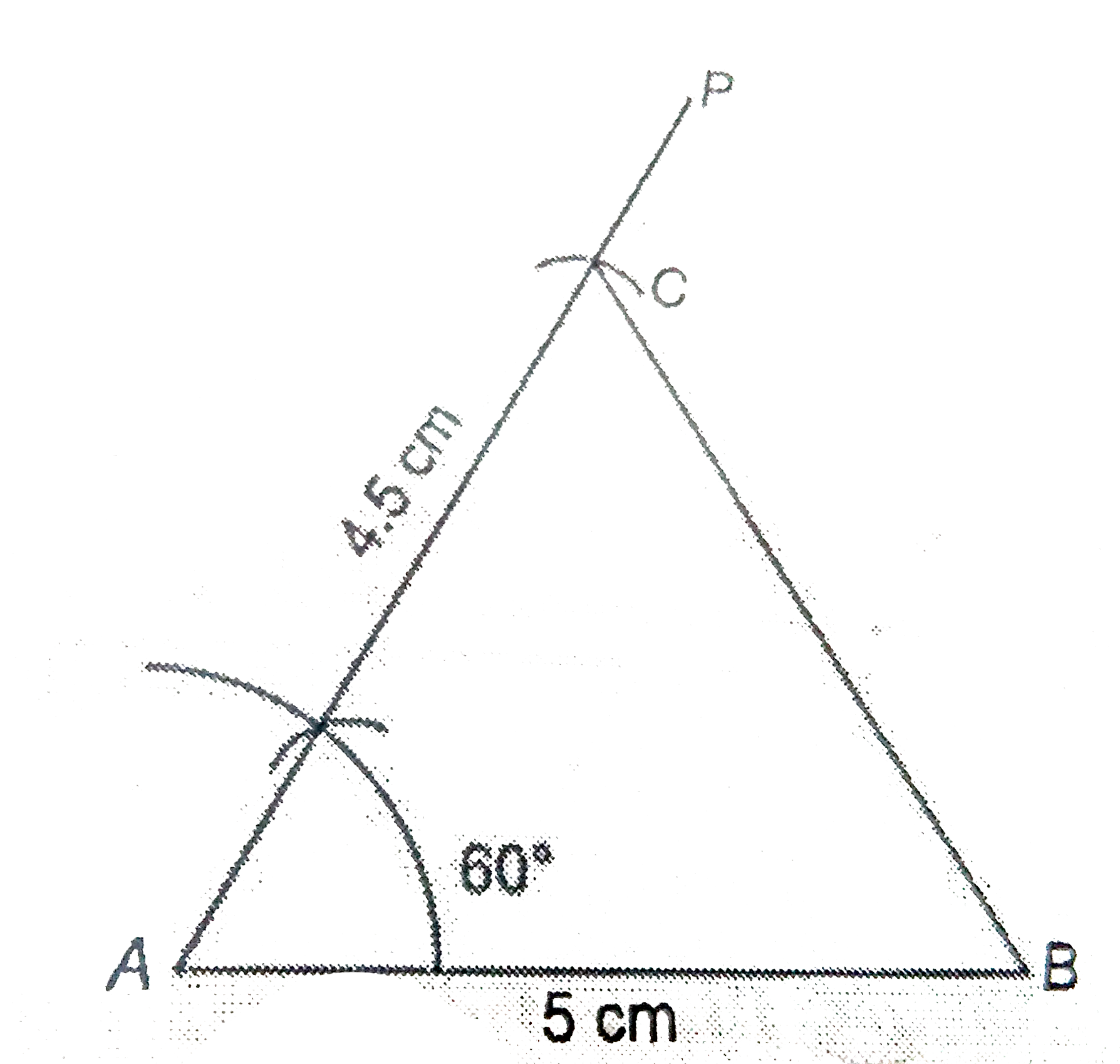
|
|
| 90. |
Represent geometically the following numbers on the number line sqrt4.5 |
|
Answer» `sqrt4.5` Now, draw a semi-circule with CENTRE O and radius OA. Let us draw BD prependicular to AC passing through point B and intersecting the semi-cricule at point D. Hencethe distance `BD is sqrt45` units. Draw an arc with centre B and radius BD, meeting AC produced at E , then `BE= BD= sqrt4.5 ` units. 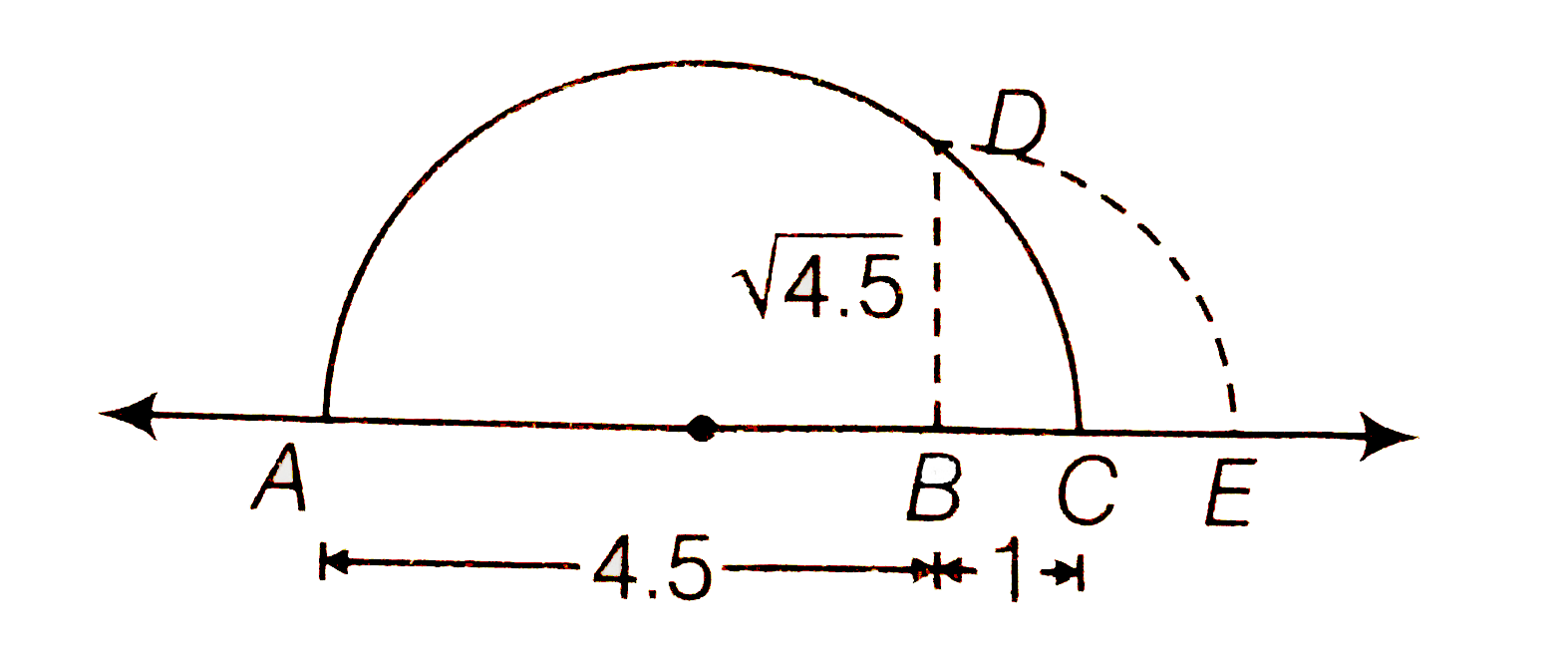 (ii) Firstly, we draw a line segment AB=5.6 units and extendit to C such that BC= 1 units. Let O be the mid point of AC. Now, draw a semi- cicule with centre O and radius OA. Let us draw BD perpendicular to AC passing through point B and intersecting the semi-cirule at point D. Hence, the distance BD is `sqrt5.6` units. Draw an arc with centre N and radius BD, meeting AC produced at E, then `BE = BD = sqrt5.6` units. 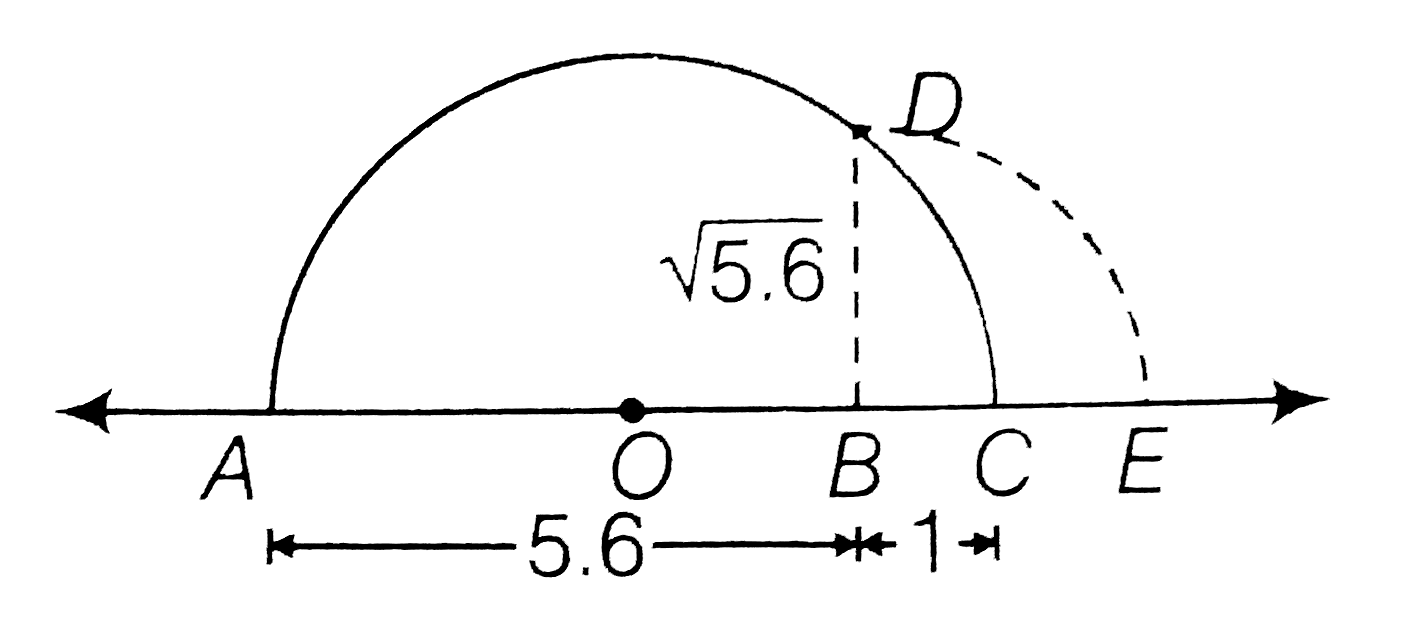 (iii) Fistly, we, draw a line segment AB = 8.1 units and extend to Csuch that BC = 1 unit LetO be the mid - POINTS of AC. Now, draw a semi-circle with centre O and radius OA. Let us draw BD prependicular to AC passing through point B intersecting the semi-circle at point D. Hence, the distance BD is `sqrt8.1` units. Draw an arc with centre B and radius BD, meeting AC produced at E, then `BE=BD=sqrt8.1` units. 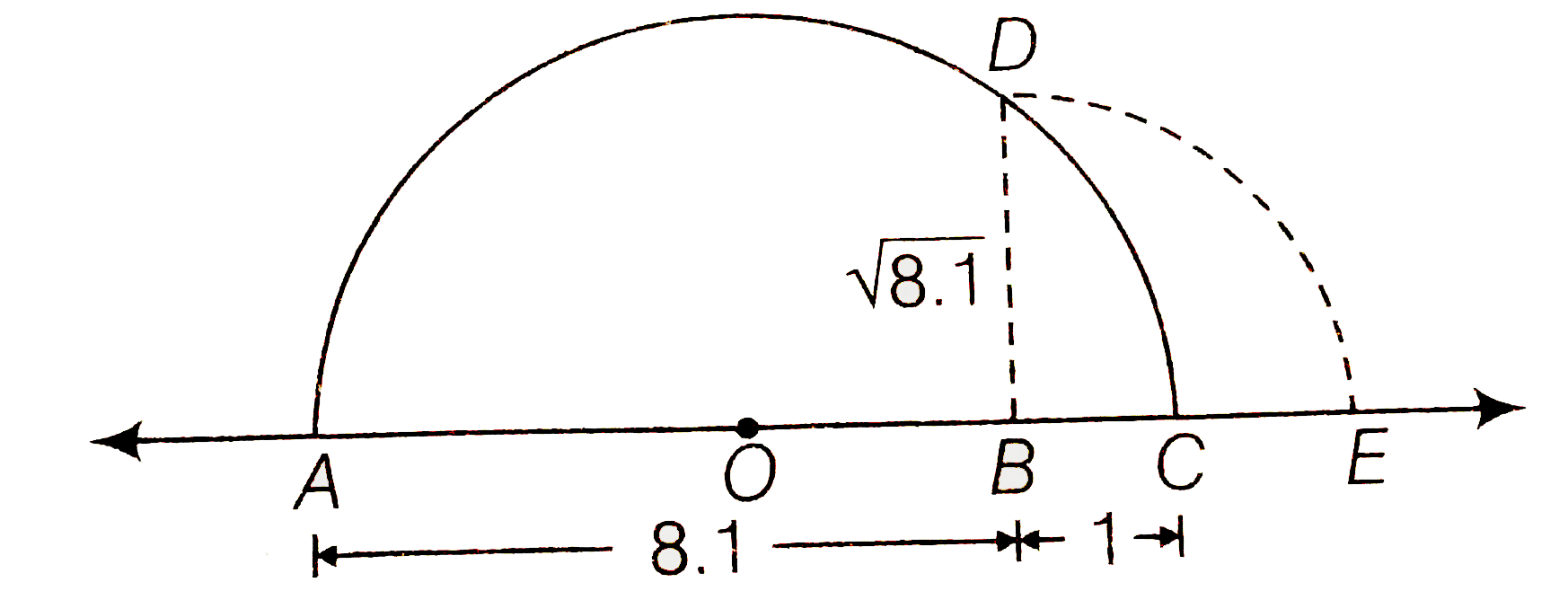 (iv) Firstly, we draw a line segment AB = 2.3 units and extend it to C such that BC=1 units , let O be the mid -point of AC. Now, draw a semi-circule with centre O and radius OA. let, us draw BD perpendicularto AC passing through point B and intersecting the semi-cricle at pointD. Hence the distance BD is `sqrt2.3` units. Draw, an arc with centre BD , meeting AC produced at E then `BE = BD= sqrt2.3` units. 
|
|
| 91. |
Draw the graph of each of the following : (i)(x)/(3)+(y)/(5)=1 , (ii) (2x+6)/(5)=y-1 , (iii) 3x+4y=12 , (iv)3x-y=2 |
| Answer» | |
| 92. |
Factorise : 6x^(2) + 13x + 6 |
|
Answer» |
|
| 94. |
State which of the following expressions are a polynomial in one variable and which are not : 16x^(2) - 49y^(2) |
|
Answer» |
|
| 95. |
Which of the following is a true statement ? |
|
Answer» Only a unique line can be DRAWN to pass through a GIVEN point |
|
| 96. |
Represent the data in the adjacent bar graph as frequency distribution table. |
|
Answer» |
|
| 98. |
Evaluate: (2 tan 54^(@))/(cot 36^(@))-(cot80^(@))/(tan 10^(@)) |
|
Answer» |
|
| 99. |
Factorise each of the following : 27y^(3) + 125z^(3) |
|
Answer» |
|