Saved Bookmarks
Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 1101. |
If E be a random experiment or rolling a dice and S be its sample space, then if one dice is rolled If two dice are rolled, find the sample space. |
|
Answer» |
|
| 1102. |
Find the magnitude of angle A, if : 2sin^(2)A-3sinA+1=0 |
|
Answer» |
|
| 1103. |
In the given figure if PQ"||"ST, anglePQR=110^(@) and angleRST=130^(@), find angleQRS. |
|
Answer» |
|
| 1106. |
The radius of the base of a cone is 14 cm and its height is 15 cm. Find the volume of the cone. |
|
Answer» |
|
| 1108. |
Verify whether the following are zeroes of the polynomial, indicated against them : p(x) = x^(2), x=0 |
|
Answer» |
|
| 1109. |
State whether the following statements are true or false. Justify your answers. (v) sqrtn is irrational if n is not a perfect square. |
|
Answer» |
|
| 1110. |
State True or False, if 'false' write correct statement. The point which lies on both the axes is called origin. |
|
Answer» |
|
| 1111. |
P is a point equidistant from two lines l and m intersecting at point A (see figure). Show that the line AP bisects the angle between them. |
|
Answer» |
|
| 1112. |
Find p (0) p, (1) and p (2) for each of the following polynomials. (i) p (x) = x ^(2) - x +1 (ii) p (z) =z ^(3) (iii) p (y)=2 + y +2y ^(2) - y ^(3) (iii) p (z) =z ^(3) (iv)p (t) = (t-1) (t +1) (v) p (x) = x ^(2) - 3x +2 |
|
Answer» (II) `2,4,4` (III) `0,1,8` (IV) `-1,0,3` (V) `2,0,0` |
|
| 1113. |
Verify whether the following are zeroes of the polynomial, indicated against them : p(x) + 3x=1, x = -(1)/(3) |
|
Answer» |
|
| 1114. |
Curved surface area of a cone is 308 cm^(2) and its slant height is 14 cm. Find, (i) radius of the base and (ii) total surface area of the cone. |
|
Answer» (ii) ` 462 cm ^(2) ` |
|
| 1115. |
Total surface area of a hemisphere is 72 cm^(2). Then, its curved surface area is ………. cm^(2). |
|
Answer» 24 |
|
| 1116. |
Find the remainder when p (x) = x ^(3) - 6x ^(2) + 14x -3 is divided by g (x) =1-2x andverify the result by long division. |
|
Answer» |
|
| 1117. |
Construct an angle of 60^(@) using ruler and compasses only Justify your construction. |
|
Answer» Solution :STEPS OF CONSTRUCTION (i) Draw a ray `OA.` (ii) With `O` as centre and a convenient radius, draw an arc, cutting `OA` at `P`. (III) With `P` as centre and the same radius as above, draw an arc, cutting the previous arc at `Q`. (iv) JOIN `OQ` and produce it to a point `B`. Then, `angleAOB` is the required angle of measure `60^(@)`. 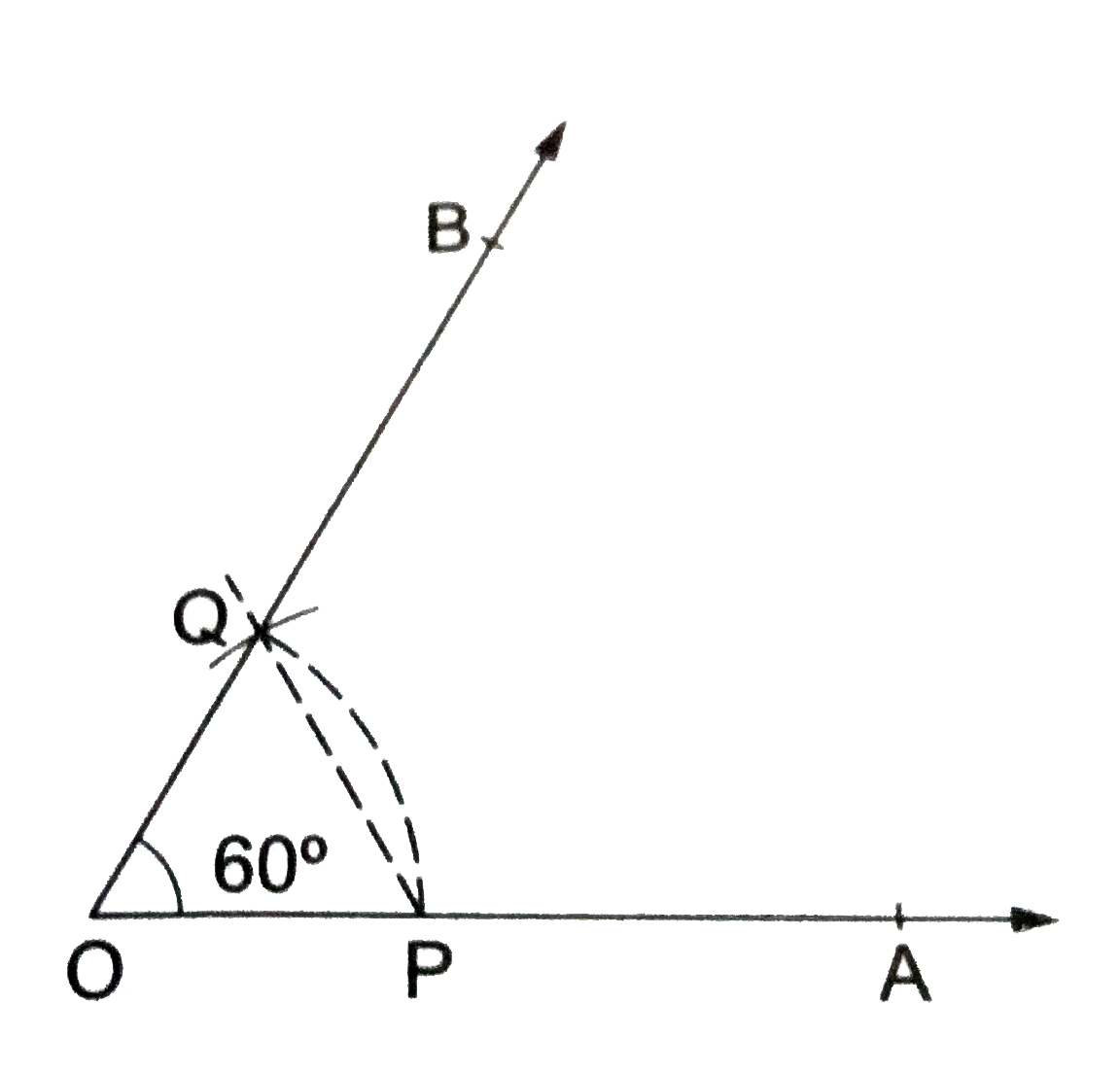 Verification : If you measure `angleAOB` by using a PROTRACTOR, you will find that `angleAOB=60^(@)`. Justification : Join `PQ`, as shown in the figure. Then, `OQ=OP=PQ` (by construction) `:. Delta OPQ` is an equilateral triangle. Hence, `anglePOQ=60^(@)` and THEREFORE, `angleAOB=60^(@)`. |
|
| 1119. |
Factorise : 12x^(2) + x -6 |
|
Answer» |
|
| 1120. |
Find the value of k, if x = 2, y =1 is a solution of the equation 2x + 3y = k. Find two more solutions of the resultant equation. |
|
Answer» |
|
| 1121. |
Find the mode of the observations 25, 20, 16, 12, 20, 16, 19, 23, 31, 20, 11, 18, 16. |
|
Answer» |
|
| 1122. |
A bus stop is barricaded from the remaining partof the road, by using 50 hollow cones made of recycled card-board. Each conehas a base diameter of 40cm and height 1m. If the outer side of each of thecones is to be painted and the cost of painting is Rs. 12 per m^2, what will be the cost of painting all thesecones (U s epi=3. 14a n dsqrt(1. 04)=1. 02)) |
|
Answer» |
|
| 1123. |
Write an algorithm to find the first 10 multiple of a given number |
| Answer» | |
| 1124. |
Twenty-seven solid iron spheres, each of radius r and surface area S are melted to form a sphere with surface area S'. Find the (i) radius r' of the new sphere, (ii) ratio of S and S'. |
|
Answer» (II) 1:9 |
|
| 1125. |
A rhombus whose diagonals are 4cm and 6cm in lengths. |
|
Answer» Solution :We know that , all SIDES of a rhombus are equal and the diagonals of a rhombus are equal and the diagonals of a rhombus are perpendicular bisectors of one another. So, to construct a rhombus whose diagonals are `4cm` and `6cm` USE the following stegs. (i) Draw the diagonal SAY `AC = 4cm` (ii) Taking `A` and `C` as centres and radius more than `(1)/(2)AC` draw arcs on both sides of the line segment AC to intersect each other. (iii)Cut both arcs intersect each other. (iv) Let PQ intersect AC at the point O. Thus , PQ is perpendicular bisector of AC. (v) Cut off `3cm` lengths from `OP` and OQ, then we get points B and D. (vi) Now , join `AB, BC, CD`, and `DA`. Thus, `ABCD` is the required rhombus. Justification Since, D and B lie on perpendicular bisector of AC. DA = DC and BA = BC....(i) [since, every point on perpendicular of line segment is equidistant from end points of line segment] Now,`angleDOC = 90^(@)` Also,OD = OB = 3cm Thus , AC is perpendicular bisector or BD. CD = CB....(ii) From Eqs. (i) and (ii), AB = BC = CD = DA Hence , ABCD is a rhombus. 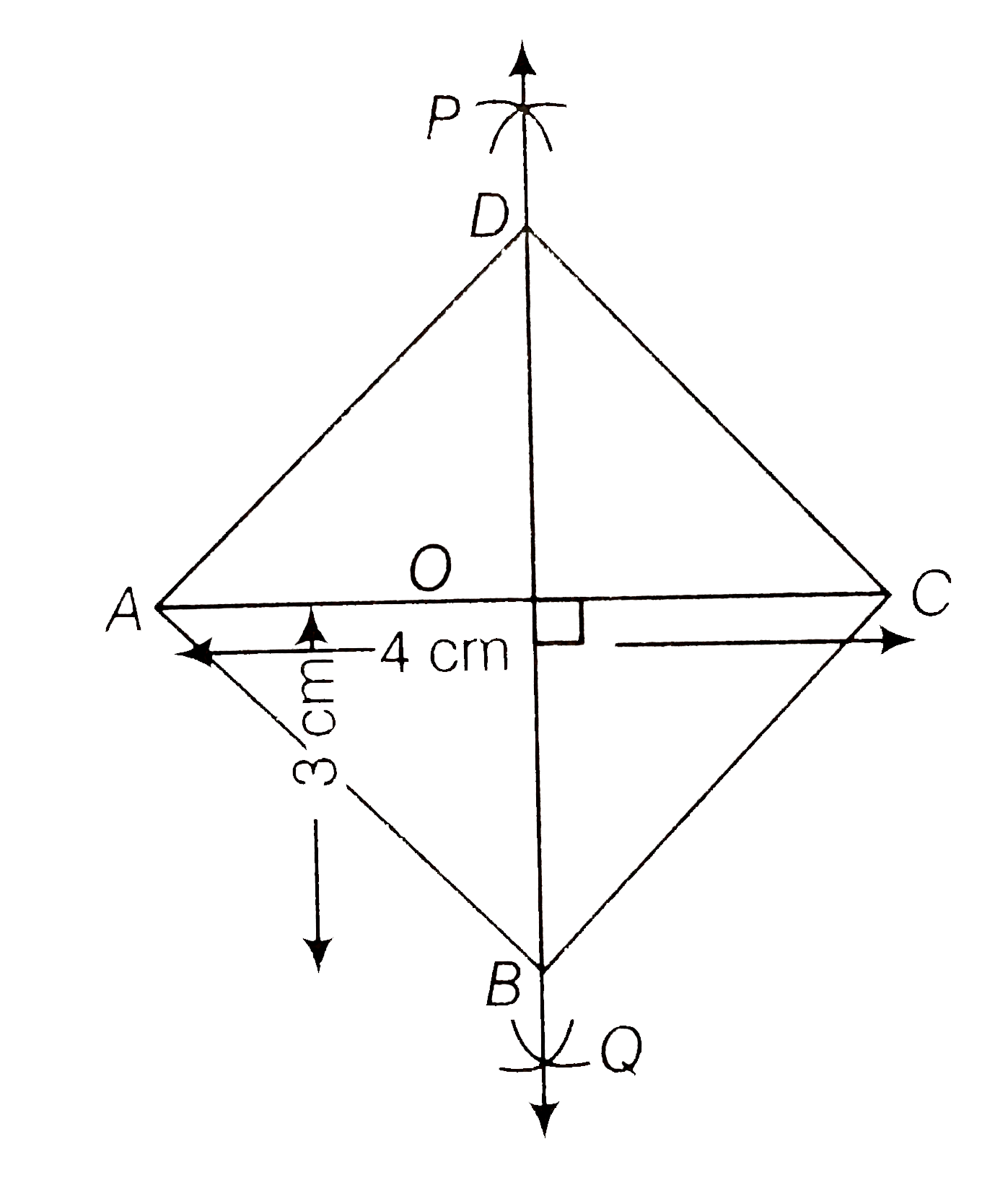
|
|
| 1127. |
Find two solutions for each of the following equations : 3y+4=0 |
|
Answer» |
|
| 1128. |
Find the magnitude of angle A, if : sin^(2)2A+sin^(2)60^(@)=1 |
|
Answer» |
|
| 1129. |
A godown measures 40 m times 25 m times 15 m. Find the maximum number of wooden crates each measuring 1.5 m times 1.25 mtimes 0.5 m that can be stored in the godown. |
|
Answer» |
|
| 1130. |
Factorise each of the following (i) 8a ^(3) + b^(3) + 12a ^(2) + 6ab ^(2) (ii) 8a ^(3) - b ^(3) -12a ^(2) b+ 6ab ^(2) (iii) 1- 64 a ^(3) -12a + 48 a ^(2) (iv) 8p^(3) - (12)/(5) p^(2) + (6)/(25) p- (1)/(125) |
|
Answer» (ii) `(2a -b) ^(3)` (iii) `(1- 4A ) ^(3)` (IV) `(2p - (1)/(5)) ^(3)` |
|
| 1131. |
If x=9−4sqrt5 then , find the value of [x^3− 1/(x^3)] |
|
Answer» `-2684sqrt(5)` |
|
| 1132. |
If 0 and 1 are the zeroes of the polynomial f (x) = 2x ^(3) - 3x ^(2) + ax +b, then find the values of a and b. |
|
Answer» |
|
| 1133. |
Fifty seeds were selected at random from each of 5 bags of seeds , and were kept under standardised conditions favourable to germination. After 20 days. the number of seeds which had germinated in each collection were counted and recorded as follows : {:("Bag",1,2,3,4,5),("Number of seeds",40,48,42,39,41),("germinated",,,,,):} What is the probability of germination of more that 35 seeds in a bag ? |
|
Answer» |
|
| 1134. |
Fifty seeds were selected at random from each of 5 bags of seeds , and were kept under standardised conditions favourable to germination. After 20 days. the number of seeds which had germinated in each collection were counted and recorded as follows : {:("Bag",1,2,3,4,5),("Number of seeds",40,48,42,39,41),("germinated",,,,,):} What is the probability of germination of more than 40 seeds in a bag ? |
|
Answer» |
|
| 1135. |
Two adjacent sides of a parallelogram are 4.5 cm and 3 cm. Find its perimeter. |
|
Answer» |
|
| 1136. |
For each of the points given below , checkwhether it is a solution of equation 2x +3y = 24 or not : (30,-12) |
|
Answer» |
|
| 1137. |
A card is drawn at random from a well shuffled pack of cards . The probability of that card being a king is ....... |
|
Answer» `1/52` |
|
| 1139. |
Evaluate the following products without multiplying directly : 103 xx 107 |
|
Answer» |
|
| 1140. |
An unbiased coin is tossed 20 times. In this experiment , 11 heads and 9tails were received. Calculate the probability of receiving head and the probability of receiving tail on the basis of the experiment . |
|
Answer» |
|
| 1141. |
Eleven bags of wheat flour, each marked 5 kg, actually contained the following weights of flour (in kg) : 4.97 5.05 5.08 5.03 5.00 5.06 5.08 4.98 5.04 5.07 5.00 Find the probability that any of these bags chosen at random contains more than 5 kg of flour. |
|
Answer» |
|
| 1142. |
If one angle of a cyclic quadrilateral is 75^(@), then the opposite angle is. . . . . . . . . . |
|
Answer» `100^(@)` |
|
| 1144. |
If P is a point on the circle with AB as a diameter, where A and B are (0, 2) and (2,4) respectively, then the locus of P is ____ |
|
Answer» |
|
| 1146. |
Factorise : 27x^(3) - 64y^(3) - 108 x^(2)y + 144 xy^(2) |
|
Answer» |
|
| 1148. |
Find out which one of thefollowingnumbers is rational and which one is irrational (i)sqrt(127) (ii) sqrt(1521)(iii) 0.285714285714… (iv) 0.101001000…. (v)7/sqrt5 (vi) 0.00010001 (vii)sqrt2 + 21 (viii)pi -2 |
|
Answer» (iv) Irrational (v) Irrational (VI) Rational (vii) Rational(VIII)Irrational |
|
| 1150. |
Evaluate the following products without multiplying directly : 104 xx 96 |
|
Answer» |
|