Saved Bookmarks
Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 1051. |
Find the difference between compound interest and simple interest on Rs 12,000 and in 1(1)/(2)years at 10% compounded half-yealry. |
|
Answer» |
|
| 1052. |
Find the difference between compound interest and simple interest on Rs 12,000 and in 1(1)/(2) years at 10% p.a. compounded yearly. |
|
Answer» |
|
| 1053. |
Curvedsurface area of a right circular cylinder is 4. 4\ m^2dotIf theradius of the base of the cylinder is 0.7m, find its height. |
|
Answer» |
|
| 1054. |
105 xx 95 |
|
Answer» 9500 |
|
| 1055. |
State whether the following statements are true or false. Justify your answers. (vi) All real numbers are irrational. |
|
Answer» |
|
| 1056. |
Factorise : 2y^(3) + y^(2) - 2y -1 |
|
Answer» |
|
| 1057. |
Construct a rhombus PQRS with diagonal PR=3.4 cm and QS =3.6 cm. |
|
Answer» Solution :Step 1: DRAW a line segment `PR = 3.4 cm.` Step 2: BISECT `PR` and mark its mid-point as `O`. Step 3: With `O` as the center and radii `1.8 cm` each, draw arcs on either SIDES of `PR` to CUT perpendicular bisector of `PR` at `Q` and `S.` Step 4: Join `PS, PQ, QR` and `RS` to form the required rhombus `PQRS.` 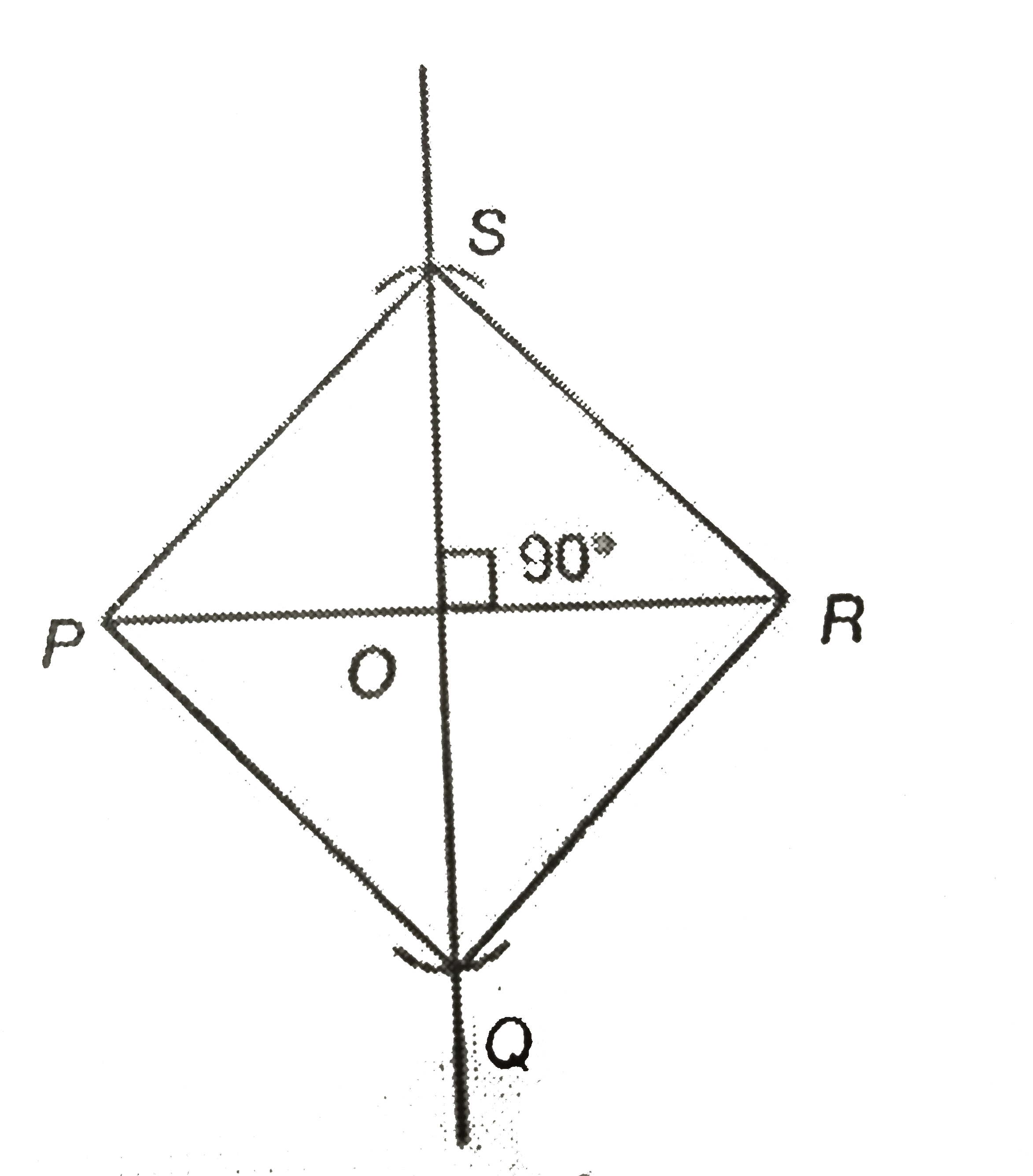
|
|
| 1058. |
Evaluate each of the following : (i){(81)^(1//5)}^(5//2)""(ii)(3sqrt(64))^(-2)""(iii)9^(3//2)+3xx4^(0)-((1)/(81))^(-1//2) (vi)sqrt((1)/(9))+(0.01)^(-1//2)-(27)^(4//3)""(v)((125)/(64))^(2//3)+((256)/(625))^(-1//4) |
|
Answer» |
|
| 1059. |
The volume of a cylinder is 2200 cm^(3) and its height is 7 cm. Then, the radius of the cylinder is ……… cm. |
|
Answer» 5 |
|
| 1060. |
A folio from the saving bank account of Mr chetan is given below .The simple interest at 4% per annum from 3-1-2003 up to 1-6-2003 is _______(approx) |
|
Answer» RS 440 |
|
| 1061. |
A spinner was spun 1000 times and the frequency of outcomes was recorded as in given table: Find (a) List the possible outcomes that you can see in the spinner(b) Compute the probability of each outcome. (c) Find the ratio of each outcome to the total number of times that the spinner spun (use the table) |
|
Answer» |
|
| 1062. |
Construct a right angled triangle whose base is 12 cm and sum of its hypotenuse and other side is 18 cm. |
|
Answer» Solution :Given that, in `DeltaABC`, base `BC = 12 cm,` `angleB = 90^(@)` and `AB + BC = 18 cm.` 1.DRAW the base `BC = 12 cm.` 2. At the point `B,` make an `angleXBC = 90^(@)`. 3. Cut a line segment `BD = AB + AC= 18 cm` from the ray `BX.` 4. Join `DC.` Draw the perpendicular bisector `PQ` of `CD` to intersect `BD` at a point `A.` 6. Join `AC.` Then, `ABC` is the required right angled triangle. 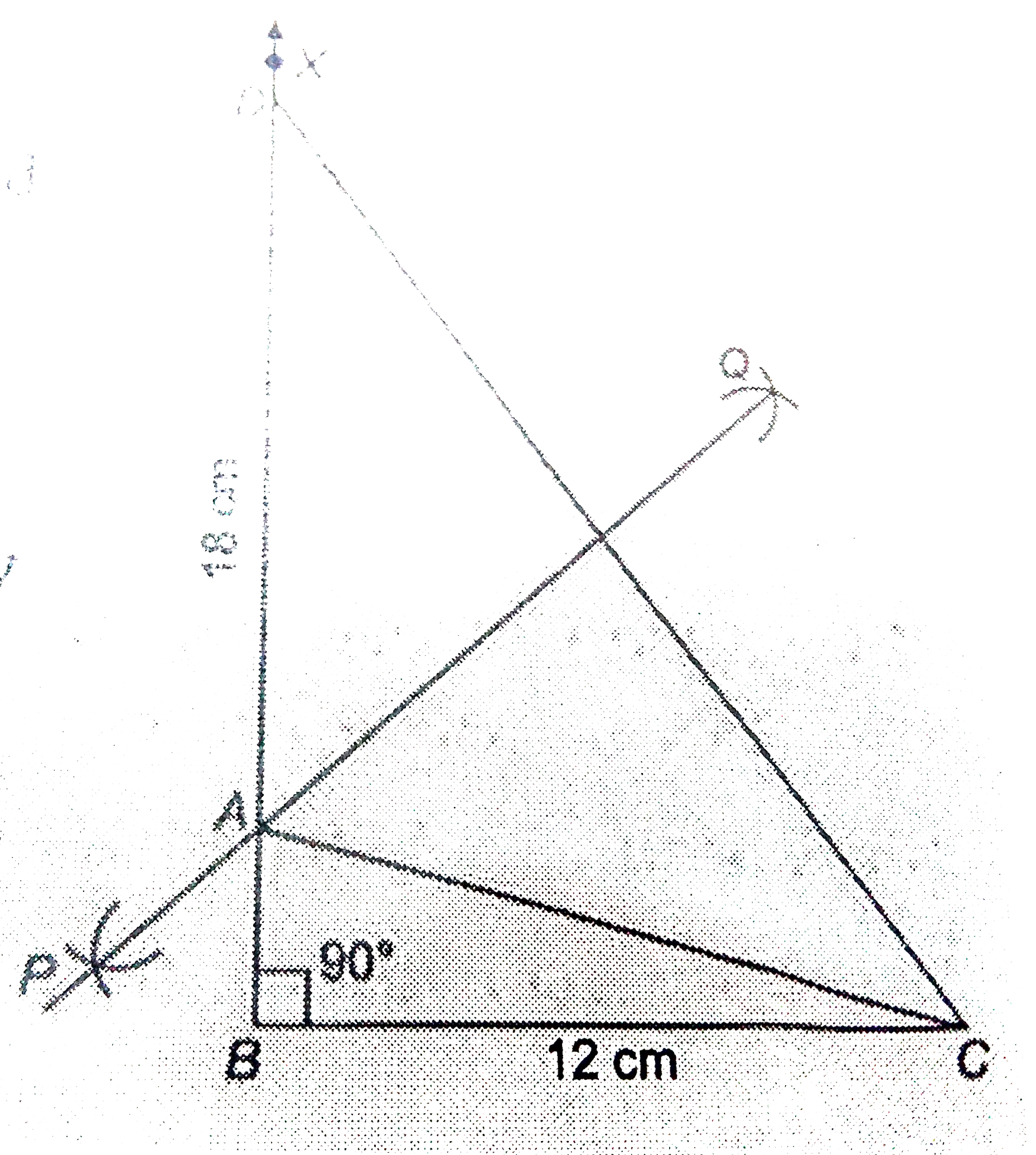
|
|
| 1063. |
Express each of the following decimal numbers in (p)/(q) form 3.bar(8) |
|
Answer» |
|
| 1064. |
Which of the following is the least attractive scheme? |
|
Answer» `5%` of Rs.120 SHARES at Rs.150. Dividend rate `=5%` Annual income/share`=(5)/(100)("Rs.120")="Rs.6"` Market value/share = Rs.150 Rate of return `=(6)/(150)(100)=4%` In a similar manner, the rates for the remaining choices can be worked out. Choice 2: Annual income/share = Rs.6.30 Rate of return `=(6.3)/(14)(100)=(9)/(2)%`. Choice 3: Annual income/share = Rs.6.30 Rate of return `=(6.3)/(125)(100)=5.04%`. Choice 4: Annual income/share = Rs.6.40 Rate of return `=(6.4)/(108)(100)=5(25)/(27)%`. The least ATTRACTIVE scheme is the sheme giving minimum rate of return. `therefore` Choice (a) gives the minimum rate of return among all the choice. |
|
| 1065. |
Is it possible to draw a triangle with sides 9 cm, 7 cm and 17 cm ? Give reason for your answer. |
|
Answer» |
|
| 1066. |
A random survey of the number of children of various are groups playing in park was found as follows : Draw a histogram to represent the data above. |
|
Answer» Solution :We know that, the areas of the rectangles are proportional to the frequencies in a histogram. Here, the widths to the rectangles are varying, so we NEED to make certain modifications in the lengths of the rectangles, so that the areas are again proportional to the frequencies : 1. SELECT a class interval with the minimum class size. The minium class size is 1. 2. The lengths of the rectangles are then modified to be proportionate to the class size 1. Now, we get the FOLLOWING table:  So, the correct histogram with varying width is GIVEN ahead. 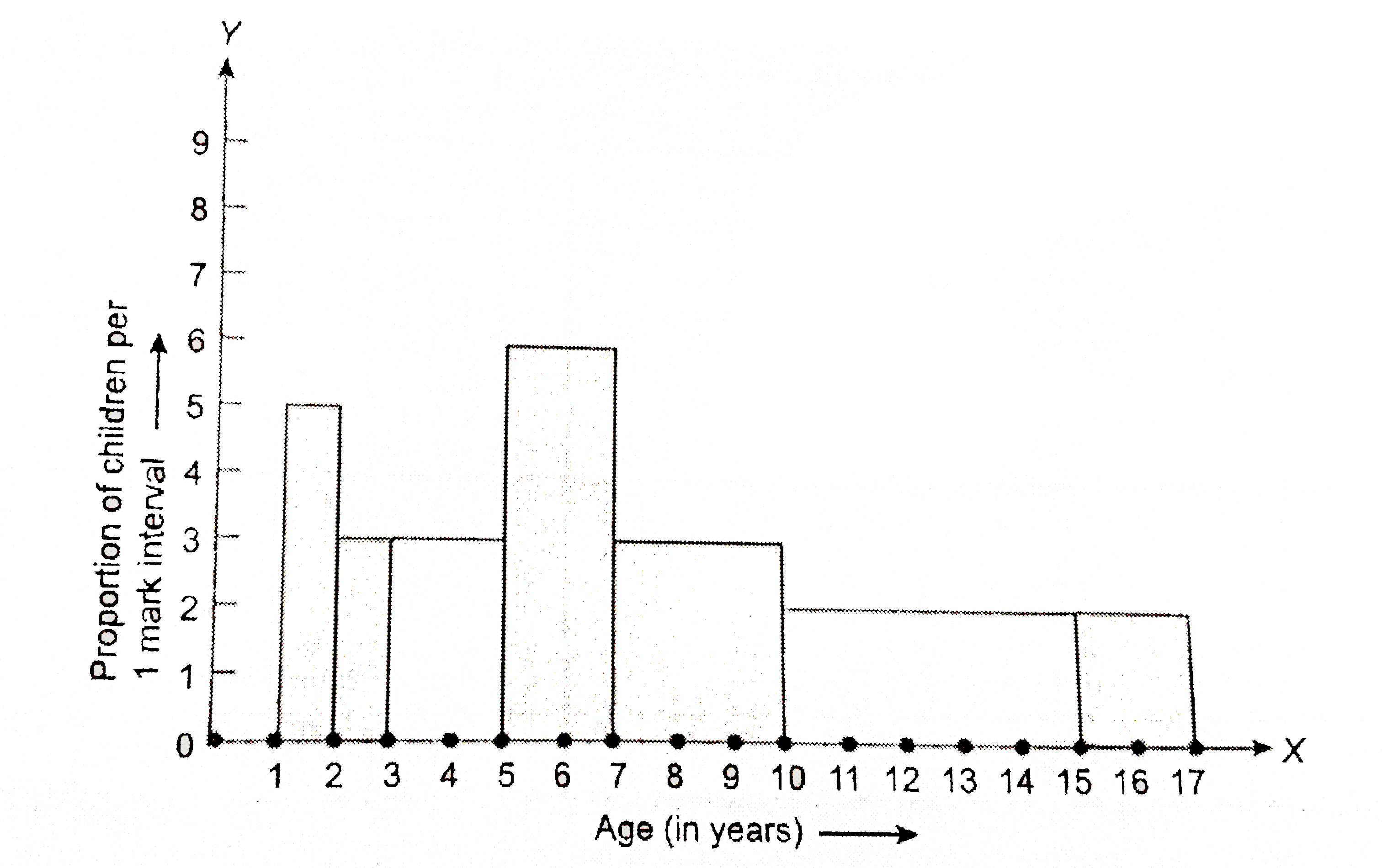
|
|
| 1067. |
Write which of the following are true and which are false? (i) Every ray has a finite length. (ii) Two lines intersect at a point. (iii) A terminated can be produced indefinitely on both the sides. (iii) A terminated line can be produced indefinitely on both the sides. (iv) A segment has one end point only. (v) If two circles are equl, then their radii are equal. (vi) The ray AB is same as the ray BA. |
|
Answer» |
|
| 1068. |
A taxi charges .Rs 20 for the first kilometre and @ .Rs per km for subsequent distance covered. Taking the total distance covered as x km and total fare .Rs y, write a linear equation depicting the relation between x and y. Draw the graph between x and y. Form your graph, find the taxi charges for covering (a) 12 km and (b) 20 km. |
|
Answer» Solution :The REQUIRED linear equation is given by `y=20+12(x-1) rArr y=8 + 12x""`…(i) Putting `x=1" in (i), we get"y= ( 8+12 xx 1) = 20.` `x=6 " in (i), we get " y = ( 8 + 12 xx 6) = 80.` Putting `x=10 " in (i) , we get " y= ( 8+ 12 xx 10) = 128.` Putting `x=15 " in (i), we get "y= ( 8 + 12 xx 15) = 188.` Thus, we have the following table: `{:(x,1,6,10,15),(y,20,80,128,188):}` On a graph paper, draw lines X'OX and YOY' as the x-axis and the y-axis respectively. Choose the scale. Along the x-axis: 1 small division = 1 km. Along the y-axis : 5 small division = .Rs 40. Now, the plot the points `A(1,20), B(6,80),C(10,128) and D(15,188).` Join AB, BC and CD to get the singlegraph line AD, as shown below. 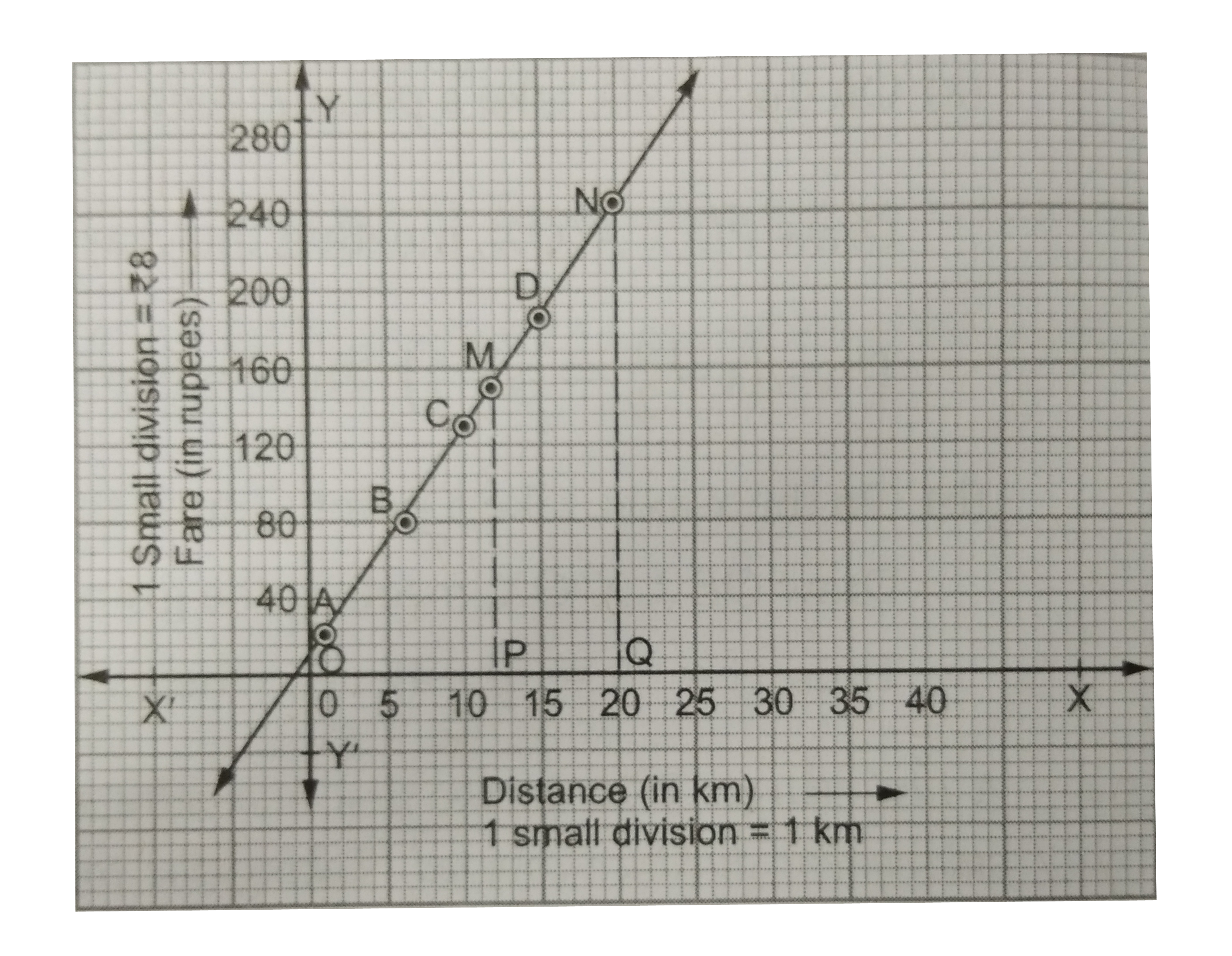 (a) On the x-axis , take a point P such that OP=12 km. Draw `PM bot X'OX` meeting the graph line at M(12,152). Thus `(x=12 rArr y=152)`, i.e., when distance COVERED is 12 km then the taxi -fare is .Rs 152. (b)On the x- axis, take a point Q such thatOQ= 20 km. Draw `QN bot X'OX`, meeting the graph line at N(20,248). Thus ,`(x= 20 rArr y= 248)` i.e., when distance covered is 20 km then the taxi -fare is .Rs 248. |
|
| 1069. |
Factorise : x^(3) - 2x^(2) - x + 2 |
|
Answer» |
|
| 1071. |
Examine, whether the following numbers are rational or irrational : (3+sqrt3)+(3-sqrt3) |
|
Answer» |
|
| 1072. |
Without actually dividing find which of the following are terminating decimals. (3)/(25) |
|
Answer» |
|
| 1073. |
Find the magnitude of angle A, if : 3cot^(2)(A-5^(@))=1 |
|
Answer» |
|
| 1074. |
The perimeter of atriangle is 300 mdotIf its sides are in theratio 3:5: 7.Find the area of thetriangle. |
|
Answer» |
|
| 1075. |
Draw a line segment 6.0 cm long and draw its perpendicular bisector. |
|
Answer» Solution :Steps of construction : 1. Draw a line `AB = 6.0 cm`. 2. With `A` as centre and a radius EQUAL to more than half of`AB` draw two arcs on both sides of line `AB`. 3. With `B` as centre draw and with same radius draw two arcs on both sides of `AB` which cut previous arcs at `C` and `D` respectively. 4. Join `C, D` which INTERSECT`AB` at POINT `X`. `X` will be the mid-point of`AB`. Then, `CD`is the required line. 
|
|
| 1076. |
Faactorise (i) 27a ^(3) + 64 b ^(3) (ii) 343 y ^(3) -1000 using the above results. |
|
Answer» (ii) `(7y -10) (49y ^(2) + 70y +100)` |
|
| 1077. |
Construct a Delta ABC in which angleB=45^(@), angleC=60^(@) and the perpendicular from the vertex A to base BC is 4.5 cm. |
|
Answer» Solution :Steps of CONSTRUCTION (i) Draw any LINE `XY`. (II) Take any point `D` on `XY` and draw `DE bot XY`. (iii) Cut off `DA=4.5` cm along `DE`. (iv) Through A draw `LM||XY` (V) CONSTRUCT `angleLAB=45^(@)` and `anglwMAC=60^(@)`, meeting `XY` at `B` and `C` respectively. Then, `DeltaABC` is the required triangle. 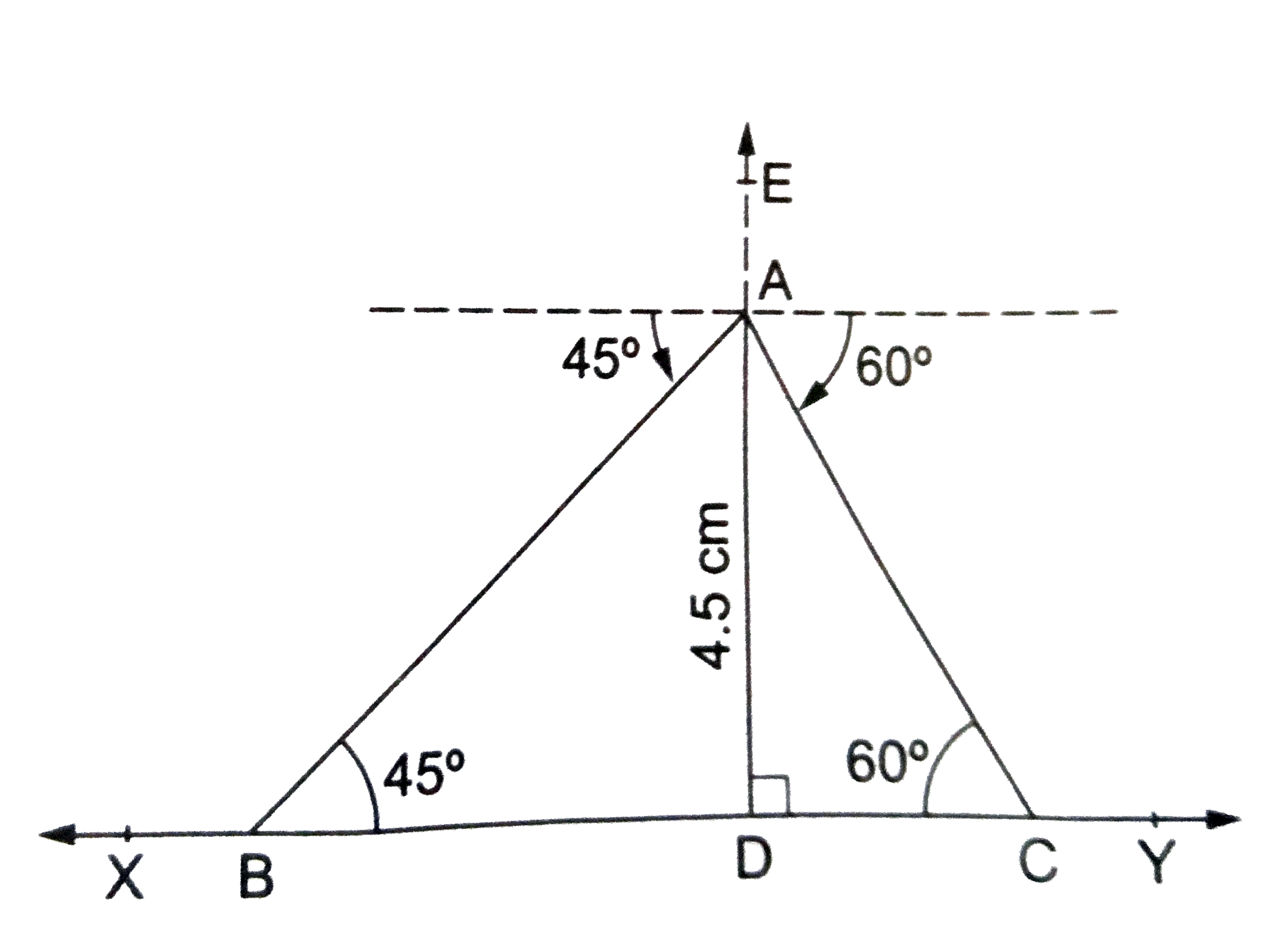
|
|
| 1078. |
IF nin N and998 < n < 1000, then express the rational number1/nin the form of a decimal fraction and state what type of decimal fraction it is . (b)If nin N and 18 < n < 20. then express the rational number 1/nin the form of decimal fraction and state what typeof decimal fraction it is . |
|
Answer» (B) ` 0.bar(9052631578947368421)` , |
|
| 1080. |
A regular square pyramid is 3m Height and the perimeter of its base is 16 m. Find the volume of the pyramid. |
|
Answer» |
|
| 1081. |
Assume that a dart will hit the dart board and each point on the dart board is equally likely to be hit in all the three concentric circles where radii of concetric circles are 3 cm, 2 cm and 1 cm as shown in the figure below. Find the probability of a dart hitting the board in the regionA. (The outer ring) |
|
Answer» |
|
| 1082. |
On the occasion of New year's day a sweet stall prepared sweet packets. Number of sweet packets and cost of each packet are given as follows. Find the mean, median and mode of the data. |
|
Answer» |
|
| 1083. |
If x = 3, y = 2 is a solution of the equation 5x - 7y = k, find the value of k and write the resultant equation. |
|
Answer» |
|
| 1084. |
Find the total surface area of a cone with diameter 7 cm and slant height 16.5 cm. |
|
Answer» |
|
| 1085. |
State the degree of each the following polynomials : 4x^(3) + 2x^(2) - 5x + 7 |
|
Answer» |
|
| 1086. |
If A={:[(-3,4),(-2,3)]:}, then show that A^(2)=I. |
| Answer» | |
| 1087. |
If A,B and C are three pointson a line and B lies between A and C (as shown in the given figure), then prove that AB+ BC= AC |
Answer» SOLUTION : It is CLEAR from the GIVEN figure that AC coincides with AB+BC By Euclid 's AXIOM 4 we know that the things that coincide with one another are equal to one another `THEREFORE` AB+BC=aC |
|
| 1088. |
10 conical Joker's caps with radius 14 cm and height 48 cm are to be made using paper sheet. Find the area (in cm^(2)) of paper sheet required. |
|
Answer» |
|
| 1089. |
The mode of the observations 17, 10, 13, 18, 19, 22, 13, 26, 9, 13 is …………….. |
|
Answer» |
|
| 1090. |
A TV channel or organised SMS (Short Message Service) poll on prohibition on smoking giving options like A- complete prohibition, B- prohibited in public places only, C- not necessary, SMS results in one hour were Represent the amount of data is grouped frequency distribution table. How many appropriate answers were received? What was the majority of peoples' opinion? |
|
Answer» TOTAL appropriate answers=65 Majority of PEOPLE's opinion=B (PROHIBITION in public places only) |
|
| 1092. |
If the triangle ABC in the Question 7 above is revolved about the side 5 cm, then find the volume of the solid so obtained. Find also the ratio of the volumes of the two solids obtained in Question 7 and 8. |
|
Answer» RATIO = 5:12 |
|
| 1094. |
The perimeter of a right-angled triangle is 60 cm and hypotenuse is 26 cm. Find the lengths of its other two sides. |
|
Answer» |
|
| 1095. |
(a)If x + y + z=0, show that x ^(3) + y ^(3) + z ^(3)= 3 xyz. (b) Show that(a-b) ^(3) + (b-c) ^(3) + (c-a)^(3) =3 (a-b) (b-c) (c-a) |
|
Answer» |
|
| 1096. |
If two sides of a triangle are 8 cm and 13 cm, then the length of the third side is between a cm and b cm. Find the values of a and b such that a is less than b. |
|
Answer» |
|
| 1097. |
For each of the points given below , checkwhether it is a solution of equation 2x +3y = 24 or not : (3,2) |
|
Answer» |
|
| 1098. |
The volume of a cone is462 m^(3). Its base radius is 7m. Find its height. |
|
Answer» |
|
| 1099. |
If the quotient obtained on dividing3x^(3) _11x^(2) _34x+ 106byx-3is3x^(2) +ax+b.then find a, b and also the remainder. |
|
Answer» |
|
| 1100. |
A hemispherical bowl of internal diameter 36 cm. contains a liquid. This liquid is to be filled in cylindrical bottles of radius 3 cm and height 6 cm. How many bottles are required to empty the bowl? |
|
Answer» |
|