Saved Bookmarks
Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 1201. |
Classify the following numbers as rational or irrational. (sqrt2-2)^(2) |
|
Answer» |
|
| 1202. |
Factorise : 9x^(2) + 25y^(2) + 49z^(2) - 30xy - 70 yz + 42 zx |
|
Answer» |
|
| 1203. |
A conical tent with radius 5 m and slant height 14 m is to be made. How many metres of 2 m wide tarpaulin will be required ? |
|
Answer» |
|
| 1204. |
RAM and Shyam are two student of Class IX. They give equal donation to a blind school in the month of March. In April each student double their donation.(a) compare their donation in April.(b) which mathematical concept have been covered in this question? |
|
Answer» (B) Euclid's AXIOM |
|
| 1205. |
Find the volume of a sphere whose surface area is 154 cm^(2). |
|
Answer» |
|
| 1206. |
Construct a square of side 3 cm. |
|
Answer» Solution :We know that, each angle of a square is right angle (i.e., `90^(@)`). To construct a square of side `3 cm`, use the following steps. (i) Draw a LINE segment `AB` of length `3cm` . (ii) Now, generate an angle of `90^(@)` at points `A` and `B` of the SEGLE of `90^(@)` at points `A` and `B` of the segment and plot the parallel LINES `AX` and `BY` at these points. (iii) Cut `AD` and `BC` of length `3 cm` from `AX` and `BY`, respectively. (iv) Draw an angle of `90^(@)` at any one of the point `C` or `D` and join both points by a line segment `CD` of length `3cm`. Thus , `ABCD` is the required square of side, `3cm`. 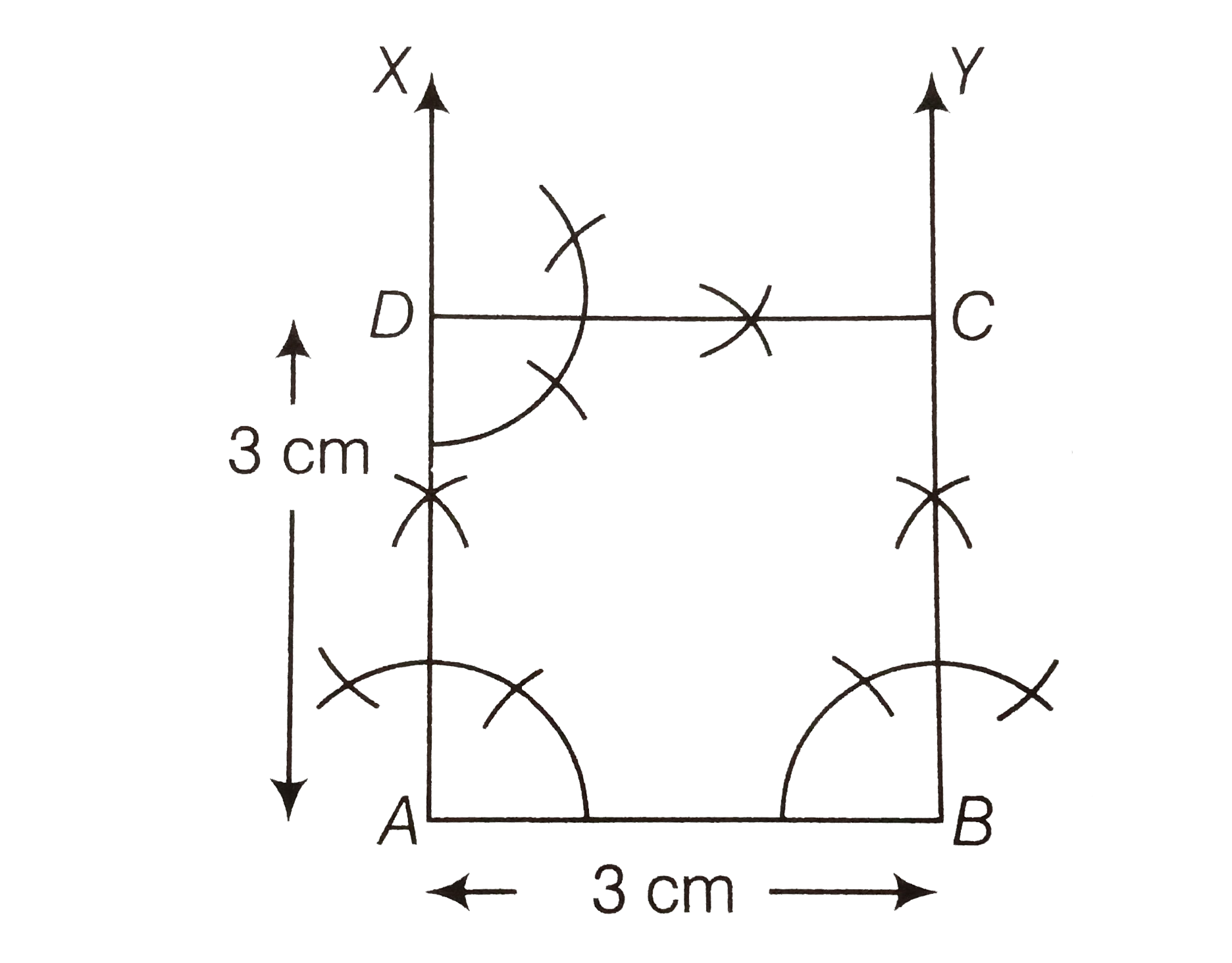 Alternate Method To construct a square `ABCD` of side `3cm`, use the following steps (i) Draw a line segment `AB` of length `3cm` . (ii) Now, draw an angle `XAB = 90^(@)` at point `A` of line segment `AB.` (iii) Cut a line segment `AD = 3cm` from the ray `AX` and join `BD`. (iv)Now, from `D` point `C` is at a distance of `3cm` . So, having `D` as centre, draw an arc of radius `3cm`. (v) From `B`,point `C` is at a distance of `3cm`. So, having `B` as center, draw an arc of radius `3cm` which intersect PREVIOUS arc (obtained in step iv) at `C`. (vi) join `DC` and `BC`. Thus, `ABCD` is the required square of side `3cm.` 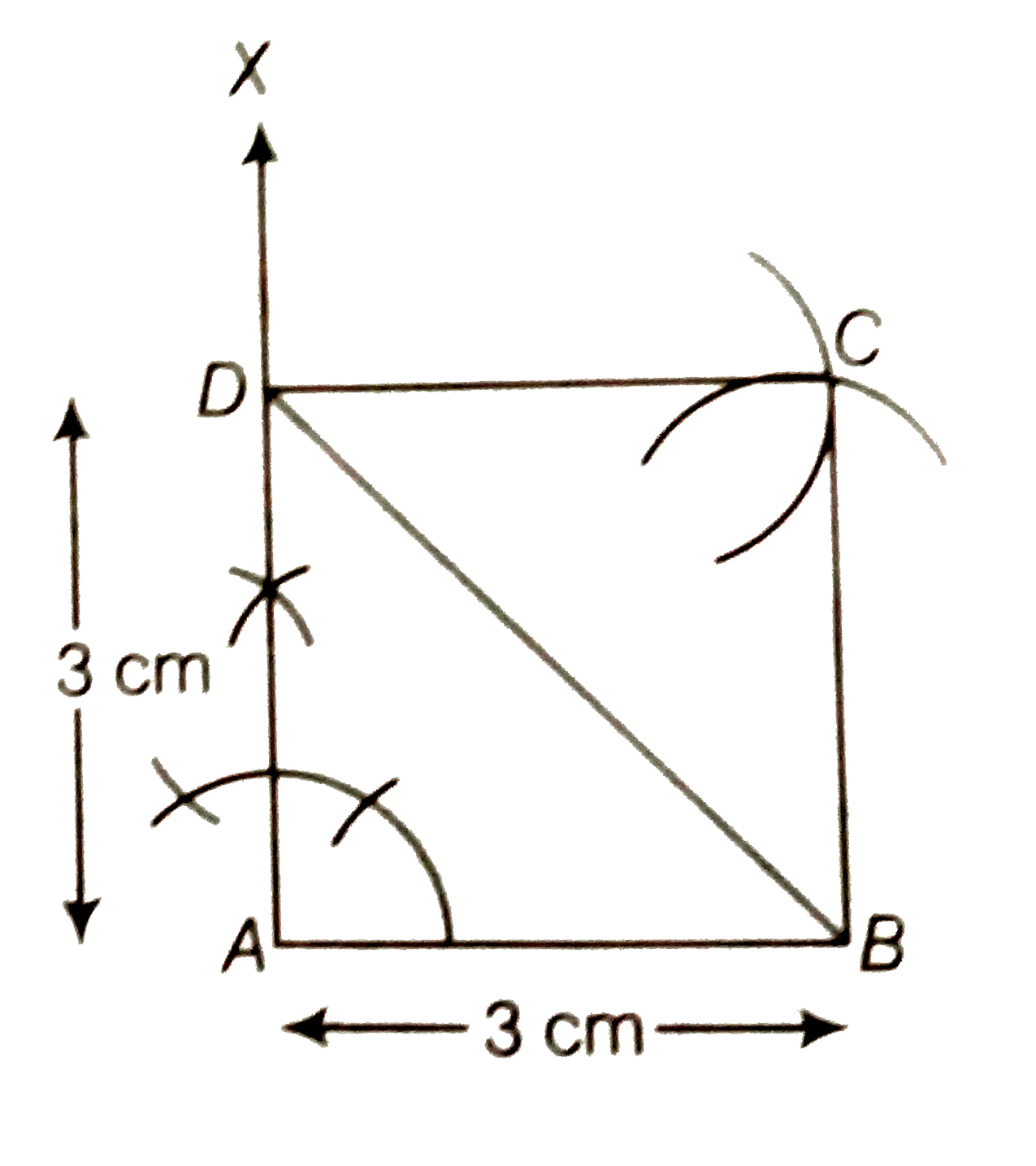
|
|
| 1207. |
Evaluate the following using suitable identites. (i) (99) ^(3) ""(ii) (102) ^(3) ""(iii) (998) ^(3) ""(iv) (1001)^(3) |
|
Answer» (II) `10,61,208` (III) `99,40,11,992` (IV) `100,30,03,001` |
|
| 1208. |
Three person X, Y andZ started a business withinvestments in theratio of 3:2:4. Theratio of their periodsof investments is 5: 6: 7. Thedifferense in theshares of profits of X and Z is whatpercentage of the share of profitof Y at theend of the year (Approximately) |
|
Answer» `120%` |
|
| 1209. |
If x,y,zin Zthen (x +y)z = x, z +y , z - this law is called |
|
Answer» COMMUTATIVE law for ADDITION |
|
| 1210. |
Evaluate each of the following using proper identity : (103)^(3) |
|
Answer» |
|
| 1211. |
The opposite angles of a parallelogram are (3x-2)^(@) and (x+48)^(@). Find the measure of each angle of the parallelogram. |
|
Answer» |
|
| 1212. |
Find the mean deviation (approximately) about the mode for the following ungrouped data: 20, 25, 30, 18, 15, 40. |
|
Answer» 6.71 |
|
| 1213. |
Find the surface area of a sphere of radius : (i) 10.5 cm(ii) 5.6 cm(iii) 14 cm |
|
Answer» (ii) 394.24 `cm^(2)` (iii) 2464 `cm^(2)` |
|
| 1214. |
Use the graphical method to find the value of k if: (i)(k-3) lieson the straight line 2x+3y =1 (ii) (5,k-2) lies on the straight line x-2y + 1=0. |
| Answer» | |
| 1215. |
The volume of a sphere is 1437""1/3cm^(3). Find its surface area. |
|
Answer» |
|
| 1216. |
Two equal sums were lent at the same time at simple interest rates of 6% and 4%per annum. The first sum was recovered 2 years earlier than the second sum, and the amount in each case was Rs 930. What was the sum lent? |
|
Answer» Rs 820 ii) Let the sum be Rs P in each case and second sum RECOVERED in x years. ii) `P[1+(6(x-2))/100]=P[1+(4(x))/100]=930`. FIND x. IV) Using the above information, find P. |
|
| 1217. |
The total surface area of a closed cylinder is 528 cm^(2). If its radius is 7 cm, find its height. |
|
Answer» |
|
| 1218. |
Obtain four solutions of the equation 2x + y = 7. |
|
Answer» |
|
| 1219. |
AB is a line segment and line I is its perpendicular bisector. If a point P lies on I, show that P is equidistant from A and B. |
|
Answer» |
|
| 1220. |
Factorise : x^(3) + 8y^(3) + 64z^(3) - 24 xyz |
|
Answer» |
|
| 1221. |
Curved surface area of a cone is308 cm ^(2)and its slant height is 14 cm Find.radius of the base . |
|
Answer» |
|
| 1223. |
A right triangle ABC with sides 5 cm, 12 cm and 13 cmis revolved about the side 12 cm.Find the volume of the solid so obtained. |
|
Answer» |
|
| 1224. |
angleP and angleQ are supplementary angles such that angleP=2x-5 and angleQ=3x+10. Then, find angleQ. |
|
Answer» `35^(@)` |
|
| 1226. |
For a given frequency distribution, n = 20 and sumf_i x_i = 140, then barx = .......... |
|
Answer» 20 |
|
| 1227. |
Find the sum of deviations of the following data measured from their actual mean. 10.3, 12.5, 13.7, 9.4, 8.6, 11.2, 12.1, 10.9, 13.2, 15.4, 14.7, 9.1, 14.2, 15.8, 7.8. |
|
Answer» |
|
| 1228. |
If 3 rational numbers x^(1//x) , y^(1//y) and z^(1//z) are equal and x^(yz)+y^(zx)+z^(xy)=729 , then find the value of x^(1//x) |
|
Answer» Solution :LET `x^(1//x)=y^(1//y)=z^(1//z)=k` `:." "x=k^(x) , y=k^(y)andz=k^(z)` `:." "x^(yz)=(k^(x))^(yz)=k^(xyz)` `y^(zx)=(k^(y))^(zx)=k^(xyz)` `z^(xy)=(k^(z))^(xy)=k^(xyz)` `"Now , "x^(yz)+y^(zx)+z^(xy)=729` `:." "k^(xyz)+k^(xyz)+k^(xyz)=729` `rArr" "3*k^(xyz)=729` `rArr" "k^(xyz)=243=(3)^(5)` On comparison, we GET(because `k=x^(1//x)` is rational) `rArr" "x^(1//x)=3` |
|
| 1229. |
If x = 2 and y = 5 is one of the solutions of equations 5x + 2y =k , find the value of k. |
|
Answer» |
|
| 1231. |
Write the following cubes in expanded form : (2a-3b)^(3) |
|
Answer» |
|
| 1232. |
When a balanced die is thrown, the porbability of getting 3 , is ....... |
|
Answer» `1/3` |
|
| 1234. |
Verify whether the following are zeroes of the polynomial, indicated against them : p(x) = 2x+1, x = (1)/(2) |
|
Answer» |
|
| 1235. |
Write the coefficients of x^(2) in each of the following : (pi)/(2)x^(2) + x |
|
Answer» |
|
| 1237. |
One side of a parallelogram is 10 cm. Ifits diagonals are 12 cm and 16 cm. Find the area of the parallelogram. |
|
Answer» |
|
| 1238. |
The sets of three numbers are called as Pythagorean triplets as they form the sides of a right angled triangle: (a) 3,4,5 (b) 5,12,13 (c ) 7,24,25 Multiply each number in any of the above pythagorean triplet by a non-zero constant. Verify whether each of the resultant set so obtained is also a pythagorean triplet or not. |
|
Answer» |
|
| 1239. |
If x^(2)+2x+3 is a factor of x^(4)+3px^(2)+2q, then find the value of p+q ? |
|
Answer» |
|
| 1240. |
Classify the following numbers as rational or irrational. (2sqrt8)/(7sqrt8) |
|
Answer» |
|
| 1241. |
A river 3mdeep and 40m wide is flowing at the rate of 2km per hour. How much water willfall into the sea in a minute? |
|
Answer» |
|
| 1242. |
If E be a random experiment of counting the number of telephone calls in a telephone line after regular period of time and if S be its sample space, then |
|
Answer» |
|
| 1243. |
In the given figures, OA = OB and OD = OC. Show that (i) triangleAOD = triangleBOC and (ii) AD||BC |
|
Answer» |
|
| 1244. |
Factorise 6x^(2) + 17x + 5 by splitting the middle term, and by using the factor theorem. |
|
Answer» |
|
| 1245. |
Two similar cones have volumes 12picu. Units and 96 picu. Units. Ifthe curved surface area of the smaller cone is 15 pi sq. units ,What is the curved surface area of the larger one? |
|
Answer» |
|
| 1246. |
angleABC and angleABD form a linear pair. If angleABC=30^(@), then angleABD=........... |
| Answer» Answer :C | |
| 1247. |
A regular square pyramid is 3m. Height and the perimeter of its base is 16 m. Find the volume of the payment. |
|
Answer» |
|
| 1250. |
(ix) AD, BE and CF are the three medians of Delta ABC and intersect at G. The area of the Delta ABC is 36 Sq. cm. Find (a) the area of Delta AGB and (b) the area of the quadrilateral BDGF. |
|
Answer» |
|