Saved Bookmarks
Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 201. |
Prove that: (i) cos55^(@)sin 35^(@)+sin 55^(@)cos 35^(@)=1 (ii) (tan 72^(@))/(cot 18^(@))-(cot 72^(@))/(tan18^(@))=0 (iii) sec70^(@)sin 20^(@)+cosec 70^(@)cos 20^(@)=2 |
|
Answer» |
|
| 202. |
From a solid cylinder whose height is 2.4 cm and diameter 1.4 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid to the nearest cm^(2). |
|
Answer» |
|
| 203. |
A small indoor greenhouse(herbarium) is made entirely of glass panes (including base) held togetherwith tape. It is 30 cm long, 25 cm wide and 25 cm high.(i) What is the area of theglass?(ii) How much of tape is neededfor all the 12 edge |
|
Answer» (II) 320 cm |
|
| 204. |
In abusiness A,B and C are partners .Twice A's investment isequal to C's investment Also B's investment is equalto (1)/(2) of A's investment .A's periodof investment is equal to 4 times C's periodof investment and A and Binvested for thesameperiod . If thetotalprofitat theend of the year isRs 44,000 then findthe sum of the shares of A and B in theprofit. |
|
Answer» RS 22,000 |
|
| 205. |
If 4cos^(2)x^(@)-1=0 and 0 le x^(@) le 90^(@), find : sin^(2)x^(@)+cos^(2)x^(@) |
|
Answer» |
|
| 206. |
A cuboidal tank measures 8 m times 6 m times 5 m. Find its volume. How many litres of water can it hold ? |
|
Answer» |
|
| 207. |
State the coefficient of x^(2) in each of the following polynomials : -3x^(2) + 5x + 11 |
|
Answer» |
|
| 208. |
Construct a rhombus PQRS with PQ=3.6 cm and angleP=50^(@). |
|
Answer» Solution :Step 1:Draw a line segment PQ=3.6 cm. Step 2: Construct `angleQPX=50^(@)`. Step 3: TAKING P as the center and a radius equal to 3.6 cm, draw an arc to cut `bar(PX)` at S, such that PS=3.6 cm. Step 4: From Q and S, draw two arcs with radii 3.6 cm each to meet each other at R. Step 5: Join QR and SR to form the REQUIRED rhombus PQRS. 
|
|
| 209. |
Out of 100 days, the forecast predicted by the wheather department proved to be true on 20 days chosen any one day from these 100 days. The probability that the forecast proved to be false is .......... |
|
Answer» `1/3` |
|
| 211. |
In the given figure, M and N are the mid-points of the sides DC and AB respectively of the parallelogram ABCD. If the area of parallelogram ABCD is 48cm^(2), (i) State the area of the triangle BEC. (ii) name the parallelofram which is equal in area to the triangle BEC. |
|
Answer» |
|
| 212. |
Expand each of the following, using suitable identities (-2a + 5b - 3c) ^(2) |
|
Answer» |
|
| 213. |
PQRS is a rhombus. If ar (PQRS)=40 cm^2and PR = 8 cm, then QS=___cm. |
|
Answer» 20 |
|
| 214. |
If different values of variable x are 9.8, 5.4 , 3.7 , 1.7 , 1.8 , 2.6 , 2.8 , 10.5 and 11.1 , find the mean barx |
|
Answer» |
|
| 215. |
Draw the graph of the equation 3x-4y =12. comment on: (i)x=0, y=3 is a solution of the equation. (ii) The abscissa i.e. the value of x can never be 100 units. (iii) Sum of intercept (parts made by straight line on the axes) on the axed is 7 units. (iv) Length of line segment between the axes is 5 units (v) Area of triangle formed by the line 3x-4y =12 and co ordinate axes. |
|
Answer» Solution :We have 3x-4y =12 3x=4y+12 x=4y+12 3 Let y =0 `rArr` x=4 Let y = -3 `rArr` x= 0 Table for above values  Plot the points A(4,0) and B(0,-3) on the graph paper and join them . producer this line on both sides (i)we see form the graph , that (0,3) does not lie on the given equation . so x=0 , y=3 is not the solution of 3x-4y=12 Also we can check algebraically (without seeing the graph) putting x=0 and y =3 in 3x-4y=12 we get 3(0) - (3) =12 `rArr` -12=12 which is not true. Spo , x =0,y =3 connot be the solution of given eqautio 3x-4y = 12 (ii) if we take any real value of x, then we get the corresponding value of y and vice versa from the equation 3x-4y =12 so x= 100 can also be taken (iii) From the graph we see the intercept made by line on the y axis =-3 so sum of intercepts =4+(-3)=1 There , it is not true that sunm of inteceps is 7. (iv) Since length of OA =4 units and length of OB =3 units `therefore` In RIGHT angle triangle AOB by pythagoras stheorem `AB^(2)=OA^(2)+OB^(2)` `=(4)^(2)+(3)^(2)=16+9=25` `AB=sqrt(25)=5 units` So length of line SEGMENT AB =5 units (v) Area of triangle =`(1)/(2)xxOAxxOB=(1)/(2)xx4xx3` units =6 sq units 
|
|
| 216. |
In triangleABC , P, Qand R are the midpoints of AB, BC and CA respectively . If ar(PBQR)=36 cm^2 , then ar(ABC)=____ cm^2 |
|
Answer» 18 |
|
| 217. |
For each of the points given below , checkwhether it is a solution of equation 2x +3y = 24 or not : (24,-8) |
|
Answer» |
|
| 218. |
Find the point of trisection of the line segment joinig the points A(2,-2) and B(-7,-4). |
|
Answer» |
|
| 219. |
Draw the graph of each of the following given equations: (i) y=3x, (ii) x=2y , (iii) x+3y=0 ,(iv)2x+3y=0 |
| Answer» | |
| 220. |
Evaluate each of the following using proper identity :25^(3) - 30^(3) + 5^(3) |
|
Answer» |
|
| 221. |
The value of machine depreciates everyyear at the rate of 20% of its value of the beginnning of the year (i.e the raete of depreciation is 20%). The machine eas purchased for Rs. 2,50,000 when new, and the srap value realised when sold was Rs 1,28,000. Find the numer of years that the machine was used. |
|
Answer» |
|
| 224. |
State whether the following statements are true or false? Also give reasons for your answers. a) Only one line can pass through a given point. b) All right angles are equal. c) Circles with same radii are equal. d) A line segment can be extended on its both sides endlessly to get a straight line. e) From the figure, AB gt AC. |
|
Answer» |
|
| 225. |
The mean of 15 observations is 32. Find the resulting mean, if each observation is decreased by 20% |
|
Answer» |
|
| 226. |
Classify the following as linear, quadratic and cubic polynomials : r^(2) |
|
Answer» |
|
| 227. |
In the adjacent figure, find the value of x, y, z and a, b, c. |
|
Answer» |
|
| 228. |
Centuries scored and number of cricketers in the world are given below. Find the mean, median and mode of the given data. |
|
Answer» |
|
| 230. |
Represent following on number line (i)sqrt(5)(ii) sqrt(3)(iii) sqrt(2) |
| Answer» | |
| 231. |
Sigma x (y^(3) -z^(3)) = ___ |
|
Answer» `(X - y) (y -Z) (z -x) (x + y +z)` |
|
| 232. |
Factorise : (9)/(25)x^(2) - (3)/(5)xy + (1)/(4)y^(2) |
|
Answer» |
|
| 233. |
In triangleABC, AD is an altitude . If BC=8 cm and ar (ABC)=40 cm^2, then AD= ______ cm. |
|
Answer» 5 |
|
| 234. |
If PQ = x and 'O' is the centre of the circle, then x =. . . . . . . . . |
|
Answer» 7 cm |
|
| 235. |
A DeltaPQR , given that QR = 3 cm, anglePQR = 45^(@) and QP - PR = 2 cm. |
|
Answer» Solution :Given, in`DeltaPQR`, `QR = 3 cm` `anglePQR = 45^(@)` and `QP - PR` = `2 cm ` To construct `DeltaPQR` , USE the FOLLOWING STEPS. (i) Draw the base QR of length 3cm. (ii) Make an angle XQR = `45^(@)` at point Q of base QR. (iii) Cut the line segment QS = QP - PR = 2cm from the ray QX. (iv) Join SR and draw the perpendicular bisector of SR say AB. (v) Let bisector AB intersect QX at P.Join PR Thus, `DeltaPQR` is the required triangle. Justification Base QR and `anglePQR` are drawn as given. Since, the point P lies on the perpendicular bisector of SR. `:.` PS = PR Now,QS = PQ-PS = PQ - PR Thus , our construction is justified. 
|
|
| 236. |
Add 2sqrt2+5sqrt3 and sqrt2-3sqrt2 |
|
Answer» |
|
| 237. |
Anuj and Rajesh each lent the same sum of money for 2 years at 8% simple interest and compound interest respectively. Rajesh received Rs 64 more than Anuj. Find the money lent by each and interest received. |
|
Answer» |
|
| 238. |
Factorise each of the following : 27p^(3) - (1)/(216)-(9)/(2)p^(2) + (1)/(4)p |
|
Answer» |
|
| 239. |
The perimeter of an equilateral triangle is 54 cm. Find its area using Heron's formula. |
|
Answer» |
|
| 240. |
A bus stop is barricaded from the remaining part of the road, by using 50 hollow cones made of recycled carboard. Each cone has a base diameter of 40 cm and height 1 m. If the outer side of each of the cones is to be painted and the cost of painting is Rs. 12 per m^(2), what will be the cost of painting all these cones ? (Use pi=3.14 and take sqrt(1.04)=1.02) |
|
Answer» |
|
| 241. |
A chord is at distance of 15 cm from the centre of the circle of radius 25 cm. The length of the chord is. . . . . . . . . . . |
|
Answer» 25 cm |
|
| 242. |
Use suitable identities to find the following products : (3x+4)(3x-5) |
|
Answer» |
|
| 243. |
Delta PQR is an equilateral triangle. If PQ = 10 cm. Find the area of Delta PQR using Heron's formula. |
|
Answer» |
|
| 245. |
Find the value of k, if x-1 is a factor of p(x) in each of the following cases : p(x) = x^(2) + x + k |
|
Answer» |
|
| 247. |
The weights(in grams) of 40 oranges picked at random from a basket are as follows: 40,50,60,55,30,90,75,85,70,85,75,80,100,110,70,55,30,35,45,70,80,85,95,70,75,40,100,65,60,40,100,75,110,30,45,84. Construct a frequency table as well as cummulative frequency table. |
Answer» SOLUTION :
|
|
| 248. |
State the degree of each the following polynomials : pi x^(3) + 5x^(5) + 7x^(2) - 12 |
|
Answer» |
|
| 249. |
Construct a rectangle PQRS with PQ=5.3 cm and a diagonal PR=5.8 cm. |
|
Answer» Solution :Step 1: Draw a line segement PQ=5.3 CM. Step 2: At Q, Construct `anglePQX=90^(@)` Step 3: Taking P as the center and 5.8 cm as radius, draw an ARC to cut `bar(QX)` at R. Step 4: With R and Q as centers, 5.3 cm and 5.8 cm respectively as radii, draw two arcs to intersect each other at S. Step 5: Join RS and PS to form the required rectangle PQRS. 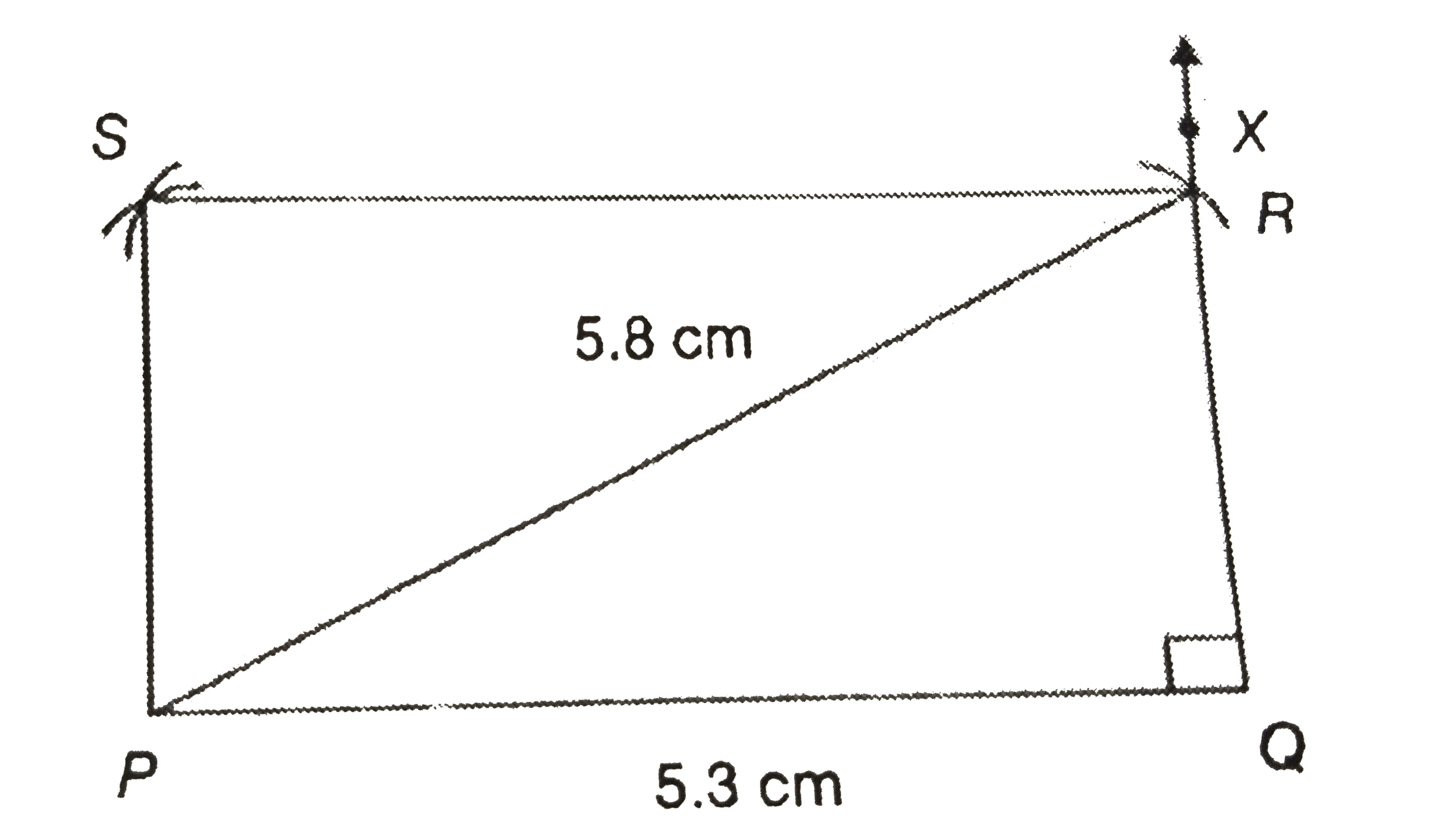
|
|
| 250. |
If each of sides of the square ABCD be a cm, then the length of each of the sides of the square, formed by joining the mid-points of the sides of ABCD is |
|
Answer» `a/2 CM` |
|