Saved Bookmarks
Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 301. |
Find the volume of a solid hemisphere with radius 30 cm. (pi=3.14) |
|
Answer» |
|
| 302. |
rationalising the denominator: (3sqrt5-sqrt7)/(3sqrt3+sqrt2) |
|
Answer» |
|
| 303. |
In the given figure, AC = AE, AB = AD and angle BAD = angle EAC. Show that BC = DE. |
|
Answer» |
|
| 304. |
State which of the following expressions are a polynomial in one variable and which are not : 7t^(2) - 5t +3 |
|
Answer» |
|
| 305. |
Ifr and s be two positiverational numbers and n is a positiveinteger, then which one of the followingis correct? |
|
Answer» NR=s |
|
| 306. |
If the rate of return from share P was 4% more, then the annual income from it would be Rs.5 more. Find its market value. (in Rs.) |
|
Answer» 125 (ii) LET the market value be x and rate of return by y. (III) `x(y+4)%-XY%=5`. |
|
| 307. |
If x +2 is a factor of x^(3) + ax^(2) + 11 x + 6, find the value of a. |
|
Answer» |
|
| 308. |
Evaluate each of the following using proper identity :18^(3) + 12^(3) - 30^(3) |
|
Answer» |
|
| 309. |
If interest is paid @ 3% simple interest per annum then the total interest (approximately) is |
|
Answer» Rs 440 |
|
| 310. |
An insurance company selected 2000 drivers at random (i.e., without any preference of one driver over another) in a particular city to find a relationship between age and accidents . The data obtained are given in following table : Find the probabilities of the following events for a driver chosen at random from the city. being 30-50 years of age and having one or more accidents in a year. |
|
Answer» |
|
| 311. |
An insurance company selected 2000 drivers at random (i.e., without any preference of one driver over another) in a particular city to find a relationship between age and accidents . The data obtained are given in following table : Find the probabilities of the following events for a driver chosen at random from the city. being 18-29 years of age and having exactly 3 accidents in one year. |
|
Answer» |
|
| 312. |
An insurance company selected 2000 drivers at random (i.e., without any preference of one driver over another) in a particular city to find a relationship between age and accidents . The data obtained are given in following table : Find the probabilities of the following events for a driver chosen at random from the city. having no accidents in one year |
|
Answer» |
|
| 313. |
If the mean of observations x,x+2,x+4,x+6 and x+8 is 11, findthe mean of the first three obervations. |
|
Answer» |
|
| 316. |
A person invests Rs 10,000 for two years at arate of 12% interset compounded annually. At the end of one years this sum amounts to Rs 11,200. Calcaultethe amount atthe end of the second year. |
|
Answer» |
|
| 317. |
Write the following cubes in the expanded form : (5p-3q)^(3) |
|
Answer» |
|
| 319. |
A farmer has a square plot of land where he wants to grow five different crops at a time. On half of the area in the middle he want to grow different crops.(A) Explain by diagram how he can divide the area to fulfill his purpose. (B) For same base and between the same parallels write the relation between area of triangle and parallelogram formed. |
|
Answer» |
|
| 320. |
Divide the polynomial x^(3) + 3x^(2) + 3x + 1 by x + pi and obtain the rem ainder. |
|
Answer» |
|
| 321. |
In the given figure we have angle1=angle3 and angle2=angle4 show that angleA=angleC |
Answer» Solution :In the given figure it is given that 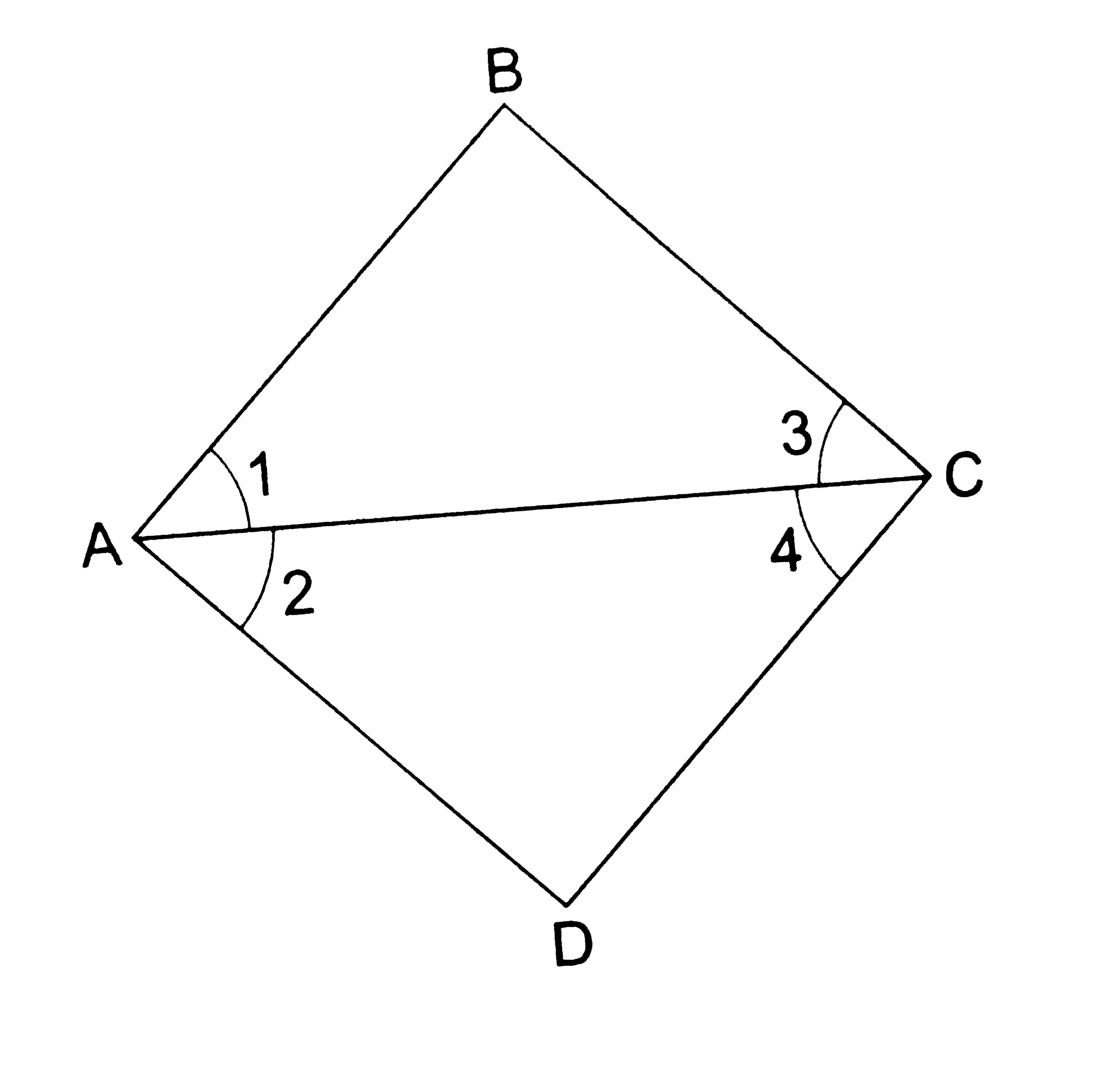 `angle1 =angle3 and angle2=angle4` By Euclid 's Axionm 2 we KNOW that when equals are added to equals the wholes are equals `THEREFORE angle(1)+angle(2)=angle(3)+angle(4) rarr angle(A)=angle(C )` HENCE `angle(A)=angle(C )` |
|
| 322. |
For each of the following polynomials, find p(0), p(1) and p(3) : p(x) =t^(3) + 2t^(2) + t - 4 |
|
Answer» |
|
| 323. |
Curved surface area of a cone is 308\ c m^2and its slant height is 14 cm. Find (i) radius of thebase and (ii) total surface area of the cone. |
|
Answer» (II) 462 `cm^(2)` |
|
| 324. |
Find the volume of the right circular cone with (i) radius 6 cm, height 7 cm (ii) radius 3.5 cm, height 12 cm |
|
Answer» (ii) 154 `cm^(3)` |
|
| 325. |
Find the values of x and y in the figures given below |
|
Answer» (iii) `x^@ = 90^@ ; y^@= 40^@` |
|
| 327. |
If x + 3 is one of the factors x^(3) + 2x^(2) - ax - 18 then a = ……… . |
| Answer» ANSWER :9 | |
| 328. |
A semicircular sheet of paper of diameter 14 cm is bent to form an open conical cup. Find the capacity of the cup. |
|
Answer» |
|
| 329. |
Monica has a piece of canvas whose area is 551 m^(2). She uses it to have a conical tent made, with a base radius of 7 m. Assuming that all the stitching margins and the wastage incurred while cutting, amounts to approximately 1 m^(2), find the volume of the tent that can be made with it. |
|
Answer» |
|
| 331. |
Total surface area of a hemisphere with radius 7 cm is ……… cm^(2). |
|
Answer» 231 |
|
| 332. |
ABCD is a parallelogram. If ar (ABC) = 18 cm^(2), then are (ABCD) = …………….. cm^(2) |
|
Answer» 18 |
|
| 333. |
A one side open cylindericaldrum has inner radius 28 cm, and height 2.1 m .How much water you can store in the drum . Express in litres .( 1 litre= 1000cc. ) |
|
Answer» |
|
| 334. |
A capsule of medicine is in the shape of a sphere of diameter 3.5 mm. How much medicine (in mm^(3)) is needed to fill this capsule ? |
|
Answer» |
|
| 335. |
A river 3 m deep and 40 m wide is flowing at the rate of 2 km per hour. How much water will fall into the sea in a minute? |
|
Answer» |
|
| 336. |
Check whether 7 + 3x is a factor of 3x^(2) + 7x. |
|
Answer» |
|
| 337. |
In the given figure ‘O’ is the centre of the circle andAB, CD are equalchords.If angleAOB = 70^@ . Find the angles of the DeltaOCD |
|
Answer» |
|
| 338. |
A traffic signal board, indicating 'SCHOOL AHEAD', is an equilateral triangle with side 'a'. Find the area of the signal board, using Heron's formula. If its perimeter is 180 cm, what will be the area of the signal board ? |
|
Answer» |
|
| 340. |
Find the zero of the polynomial in each of the following cases : p(x) = x+5 |
|
Answer» |
|
| 341. |
D is a point on side BC of triangle ABC such that AD = AC (see the given figure). Show that AB gt AD. |
|
Answer» |
|
| 343. |
Use suitable identities to find the following products : (3-2x) (3+2x) |
|
Answer» |
|
| 344. |
Factorise 4x^(2) + y^(2) + z^(2) - 4xy - 2yz + 4xz. |
|
Answer» |
|
| 345. |
In trianglePQR, angleP = angleQ = angleR. If PQ = 6, then the perimeter of trianglePQR is .......... |
|
Answer» 12 |
|
| 346. |
triangle ABC is an isosceles tr ia n g le in w h ich AB = AC. Side BA is produced to D such that AD = AB (see the given figure). Show that angle BCD is a right angle. |
|
Answer» |
|
| 347. |
Draw the graph of the equation 2x-y+3=0. Using the graph, find the value of y when (a) x=2, (b) x=-3. |
|
Answer» Solution :We have `2x-y+3=0 rArr y= 2x+3.""` …(i) Putting x=0in (i) , we get `y= (2 xx 0 + 3) = 3.` Putting x=1in (i), we get`y= ( 2xx 1 + 3) = 5.` Putting x=-1in (i), we get `y= [2 xx (-1) + 3] =1.` Putting x= -2in (i), we get `y=[2 xx (-2) + 3] =-1.` Thus, we have the following table: `{:(x,0,1,-1,-2),(y,3,5,1,-1):}` On a graph paper, draw lines X'OX and YOY' representingthe x-axis and the y- axis RESPECTIVELY. On this graph paper, plot the points A(0,3), B(1,5),C(-1,1) and D(-2,-1). Join AB, AC andCD to get a straight line BACD. Produce it in both ways to get the required graph. 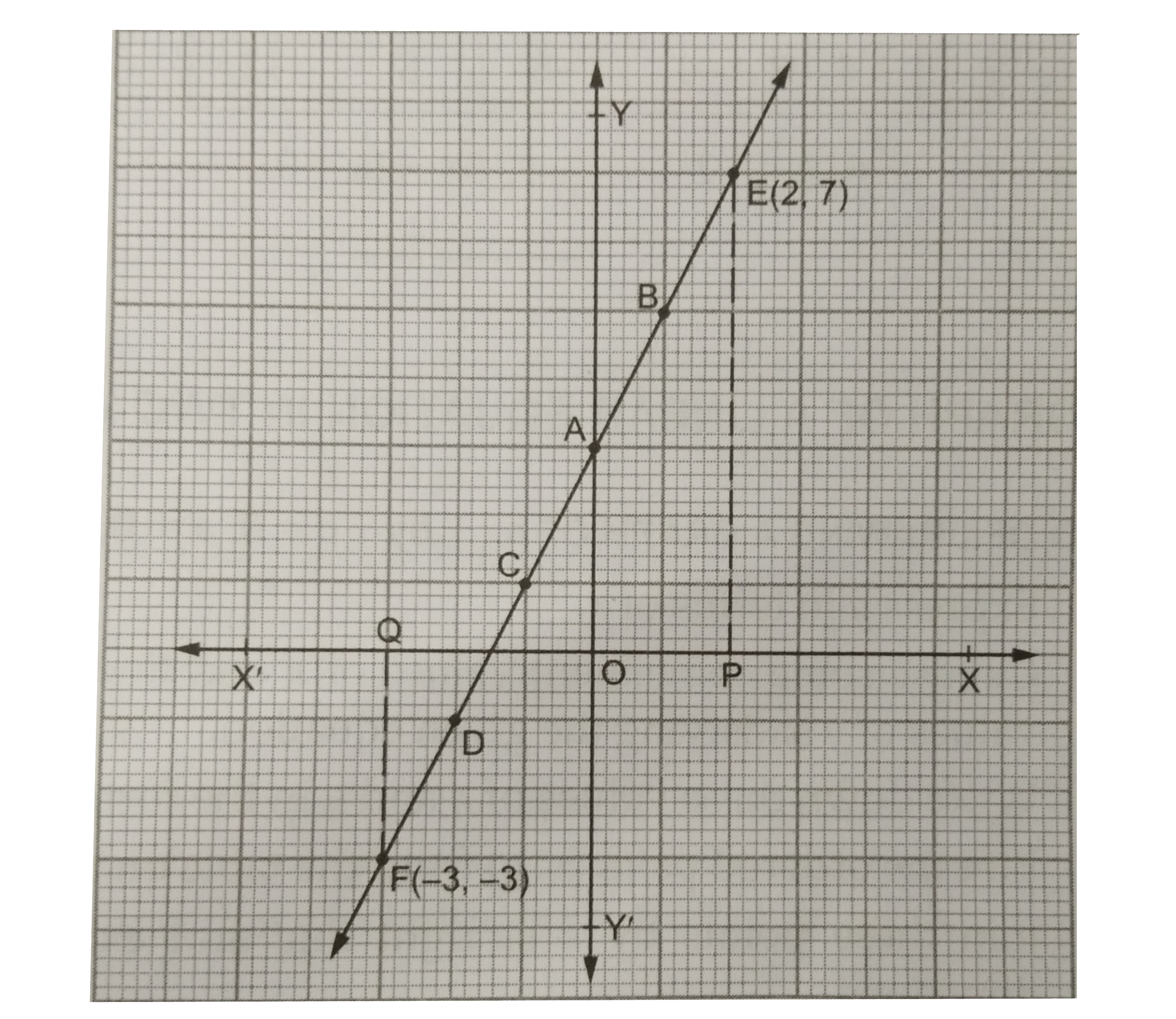 (a)On the axis, we take a point P for which x=2, i.e., OP=2. FromP, draw `PE bot X'OX`, meeting the graph line BACD produced at E. Then, E(2,7) shows that `(x=2 rArry=7),` i.e., when x=2, then y=7. (b) On the x-axis, we take a point Q for which `x=-3`, i.e., OQ = 3 units. From Q, draw `QF bot X'OX`, meeting the graph line BACD produced at F. Then, `F(-3,-3)` shows that `(x=-3 rArr y=-3)`, i.e., when x=-3, then y= -3. |
|
| 348. |
Verify whether 2 and 0 are zeroes of the polynomial x^(2) - 2x. |
|
Answer» |
|
| 350. |
Fill in the blands so as to make each of the following statements true : In parallelogram ABCD, if angleA:angleB=2:3, then angleD=…….. |
|
Answer» |
|