Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 401. |
Find the mean deviation from the mode for the following ungrouped data: 2.5, 6.5, 7.3, 12.3, 16.2. |
|
Answer» 4.34 Where A = ARITHMETIC mean. |
|
| 403. |
The runs scored by two teams A and B on the first 60 balls in a cricket match are given below: Represent the data of both the teams on the same graph by frequency polygons. |
Answer» SOLUTION :FIRST make the CLASS intervals continuous  Now, draw a FREQUENCY polygon curve. 
|
|
| 404. |
If x+3 is a factor of x^(3) +6x^(2) + 11x + k, then k =. |
|
Answer» 2 |
|
| 405. |
If a line intersects two concenteric circles (circles with the same centre) with center O at A,B,C and D, prove that AB=CD (see figure). |
|
Answer» Solution :Let OP be the perpendicular from O on line L. since, the perpendicular from the centre of a circle to a chord bisects the CHORDS. Now, BC is the chord of the smaller circle and `OP botBC` . `thereforeAP=PC`......(1) Since, AD is a chord of the LARGER circle and `OPbotAD` `therefore AP=PD` ......(2) On subtracting eq. (1) from eq. (2), we get `AP-BP=PDrArrAB=CD` 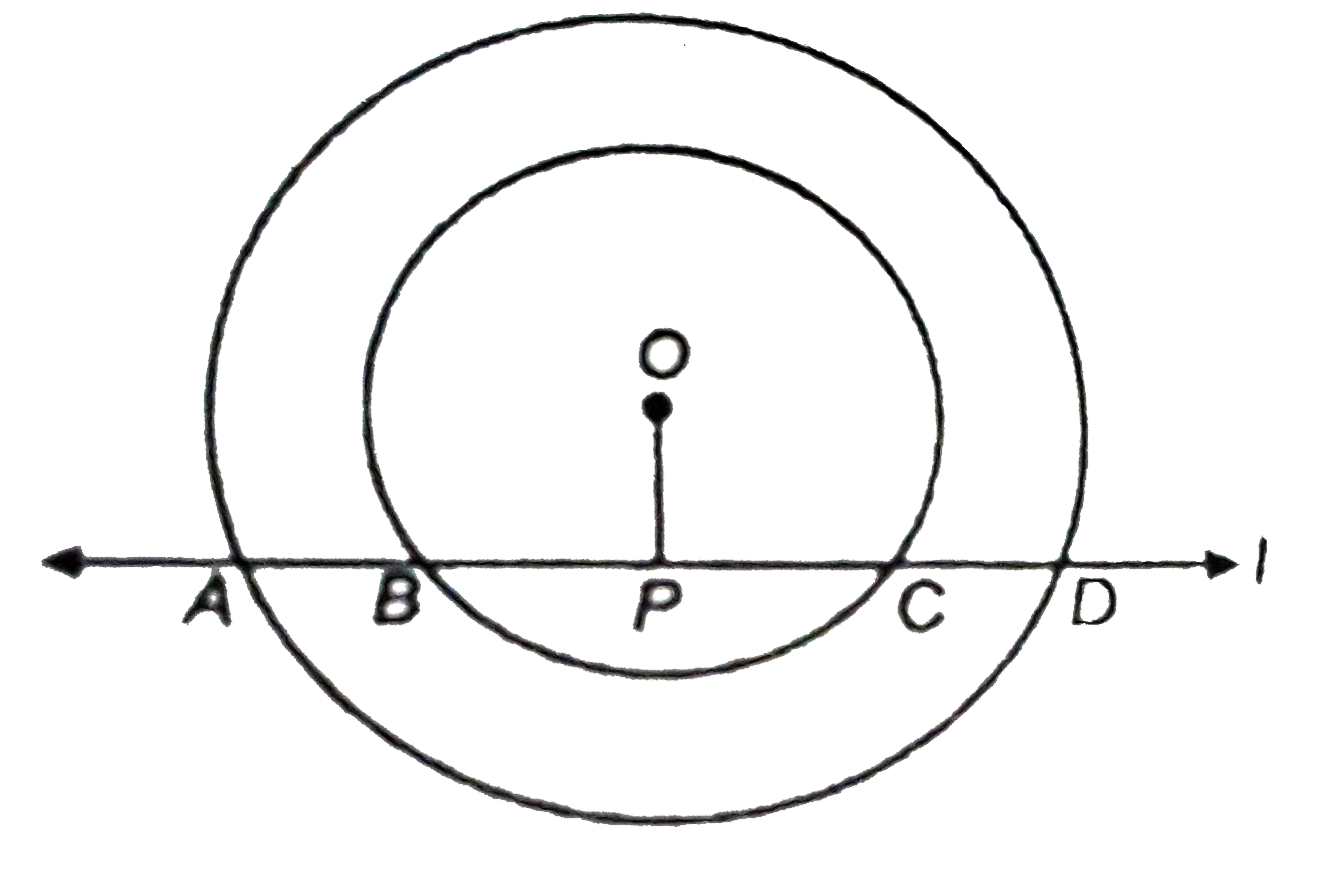
|
|
| 406. |
Factorise : 12x^(2) - 7x + 1 |
|
Answer» |
|
| 407. |
What will be the output fo the following algrothim ? |
|
Answer» `47^(@)` |
|
| 408. |
A sum of Rs 22000 is divided into three parts such that the corresponding interests earned after 1 year at 2% per annum, 4 years at 2% per annum and 16 years at 1% per annum simple interest are equal. Find the least of the sum which was lent. (in Rs) |
|
Answer» 1000 ii) LET the sum lent be RSX, Rs y and Rs `22,000=(x+y)`. ii) `(x xx 2)/(100) = (y xx2 xx 4)/100` `=(200,000-(x+y) xx 1 xx 6)/100` iv) SOLVE the above equation and find the least of the sums. |
|
| 409. |
Classify the following as linear, quadratic and cubic polynomials : x^(2) + x |
|
Answer» |
|
| 410. |
Select the correct answer (MCQ) : (v) If log(sqrtx) 0.25 = 4, "then" x = |
|
Answer» 0.5 |
|
| 411. |
AFLATOUN social and financial educational program intiated savings program among the high school children in Hyderabad district. Mandal wise savings in a month are given in the following table Find arithmetic mean of school wise savings in each mandal. Also find the arithmetic mean of saving of all schools. |
|
Answer» (II) ₹444 SAVING PER SCHOOL. |
|
| 412. |
Every point on a number line represents. |
|
Answer» a RATIONAL number |
|
| 413. |
Which one of the followings is the transitivity law ? |
|
Answer» ` x GTY Rightarrowx + Z GT y + z, AAx, y, z, in Z` |
|
| 414. |
I and m are two parallel lines intersected by another pair of parallel lines p and show that triangle ABC = triangle CDA |
|
Answer» |
|
| 415. |
The volume of a cuboid is 1200 cm ^(3)The length 15 cm .and breadth is 10 cm , Find its height |
|
Answer» |
|
| 416. |
In the following table, pass percentage of three schools from the year 2001 to the year 2006 are given. Which school students' performance is more consistent? {:(,2001,2002,2003,2004,2005,2006),("School X",80,89,79,83,84,65),("School Y",92,94,76,75,80,63),("School Z",93,97,67,63,70,85):} |
|
Answer» X (ii) The SCHOOL with the maximum pass percentage is more consisternt. |
|
| 417. |
The mean of 15 observations is 32. Find the resulting mean, if each observation is divided by 0*5 |
|
Answer» |
|
| 418. |
Mean of 15 observations is 200. If one observation is excluded, the mean of remaining observations is 198.Find the value of the excluded observation. |
|
Answer» |
|
| 419. |
Simplify : (i)3^(1//3)xx(2//5)""(ii)((1)/(2))^(1//5)xx2^(3//5) |
|
Answer» |
|
| 420. |
The surface area of a sphere is 616 cm^(2). Then, its radius is ……… cm. |
|
Answer» 6 |
|
| 421. |
If E be a random experiment or rolling a dice and S be its sample space, then if one dice is rolled then find the sample space of it and also find the probability ofnot getting 4. |
| Answer» | |
| 422. |
Draw a histogram for the marks of students given below: |
|
Answer» Solution :Here, MINIMUM class-size = 5. So, we adjust the frequencies by USING the following formula: Adjusted frequency of a class `="Minimum class-size"/"calss-size" xx "frequency of the class"` The adjusted frequencies are COMPUTED as FOLLOWS:  Now, we construct rectangles with class-limits as bases and RESPECTIVE adjusted frequencies as heights. 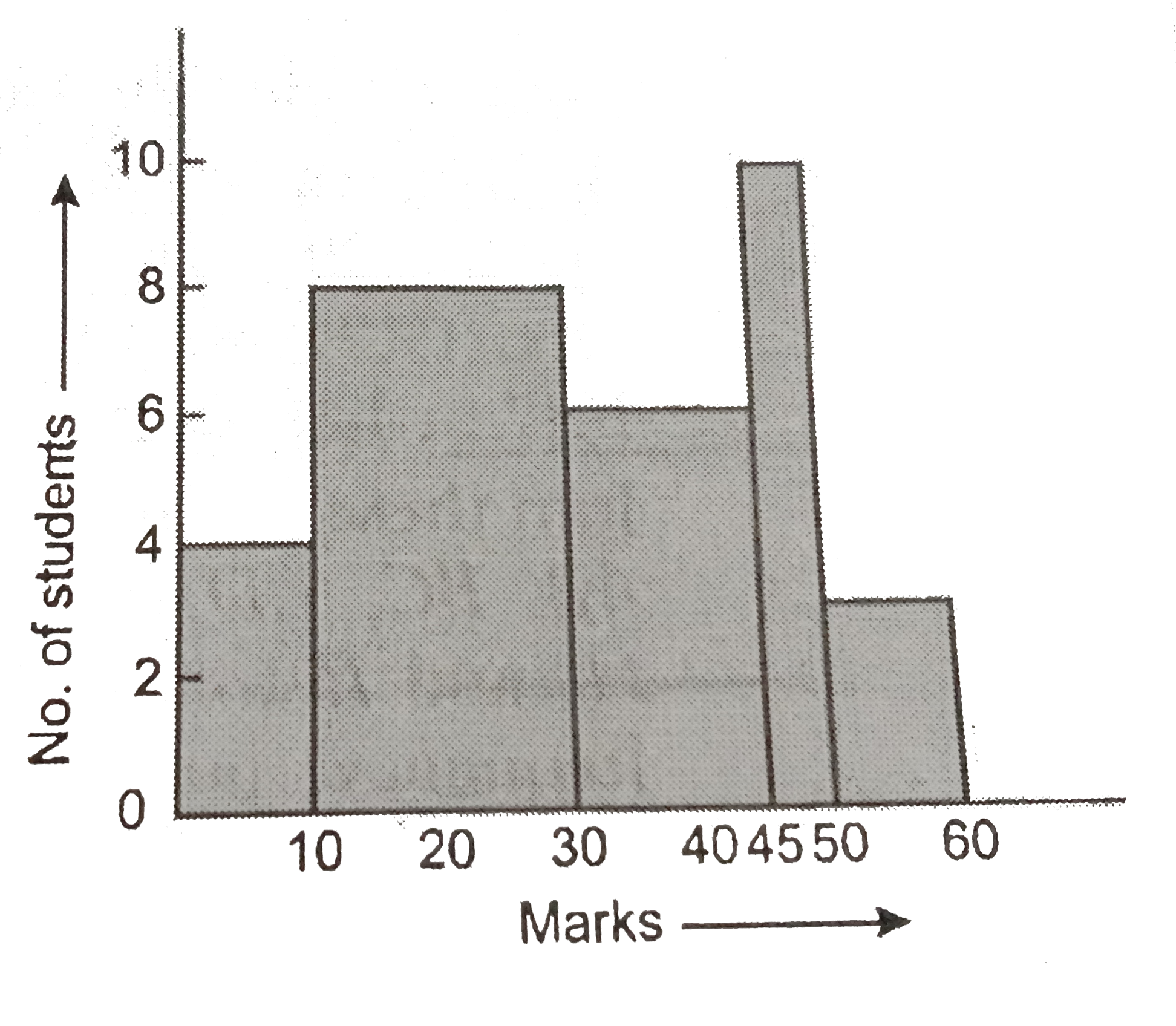
|
|
| 423. |
Write thetruth value (T/F) of the following with suitable reasons:A circle isa plane figure.Linesegment joining the centre to any point on the circle is a radius of thecircle.If a circleis divided into three equal arcs each is a major arc.A circlehas only finite number of equal chords.A chord ofa circle, which is twice as long is its radius is adiameter of the circle.Sector isthe region between the chord and its corresponding arc.The degreemeasure of an arc is the complement of the central angle containing the arc.The degreemeasure of a semi-circle is 180^0 |
|
Answer» |
|
| 424. |
For each of the following polynomials, find p(0), p(1) and p(3) : p(x) = (1)/(3)x^(2) + 4x -1 |
|
Answer» |
|
| 425. |
Construct a Delta ABC in which BC=6 cm, angleB=60^(@) and (AB+AC)=9 cm. Measure AB andAC. Justify your answer. |
|
Answer» Solution :STEPS OF CONSTRUCTION (i) Draw `BC=6` CM. (ii) Construct `angleCBX=60^(@)`. (iii) Along `BX`, set off `BP=9` cm. (iv) Join CP. (v) Draw the perpendicular BISECTOR of CP to intersect BP at A. (vi) Join AC. Then, `Delta ABC` is the required triangle. Verification : On measuring, we find that `AB+AC=(4+5)` cm `=9` cm. Justification : Clearly, A lies on the perpendicular bisector of CP. `:. AP=AC`. Now, `BP=9` cm [SEE Step (iii)] `implies AB+AP=9` cm `implies AB+AC=9 cm""[ :' AP=AC]`. Hence, `DeltaABC` is the required triangle. 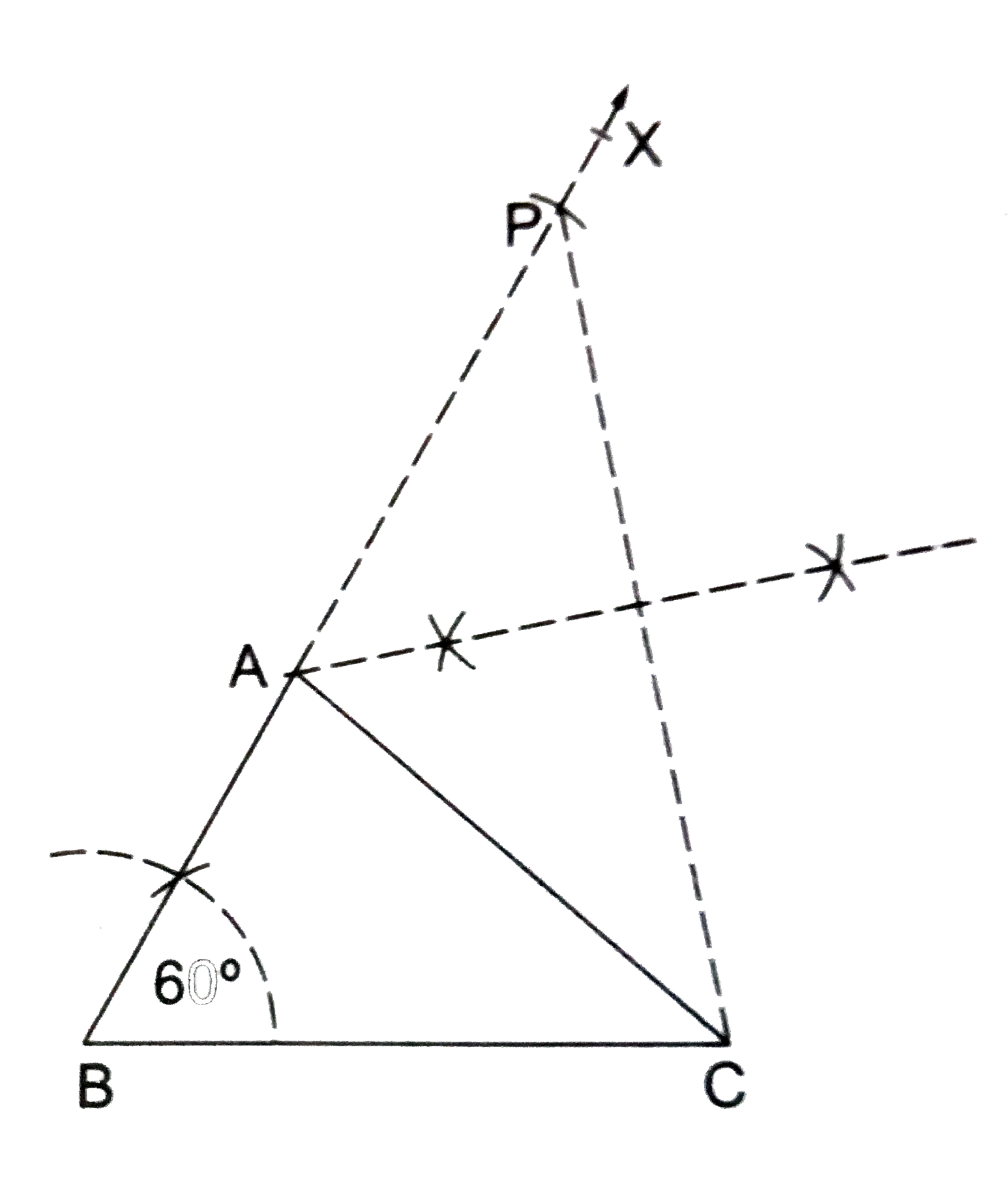
|
|
| 426. |
Divide the polynomial x^(3) - 4x^(2) + 3x +1 by each of the following divisors and find the remainder in each case : x-3 |
|
Answer» |
|
| 427. |
Divide the polynomial x^(3) - 4x^(2) + 3x +1 by each of the following divisors and find the remainder in each case : x+4 |
|
Answer» |
|
| 428. |
Divide the polynomial x^(3) - 4x^(2) + 3x +1 by each of the following divisors and find the remainder in each case : x-1 |
|
Answer» |
|
| 429. |
Divide the polynomial x^(3) - 4x^(2) + 3x +1 by each of the following divisors and find the remainder in each case : x+1 |
|
Answer» |
|
| 430. |
Factorise : 6x^(3) + 13x^(2) + 9x + 2 |
|
Answer» |
|
| 431. |
Factorise : x^(3) + 8x^(2) + 19x + 12 |
|
Answer» |
|
| 432. |
Write each of the following as an equation in two variables : x = - 5 |
|
Answer» |
|
| 433. |
Prasad invested Rs.4000 to buy type A shares of a company. He invested in the same company to buy Rs.4000 worth type B shares at face value. Market value of A equals equals face value of B. If he bought a total 64 shares of both, how many type A shares did the buy? |
|
Answer» 6 |
|
| 434. |
Find the square root of (x^(2))/(9) + (9)/(4x^(2)) - (x)/(3) - (3)/(2x) + (5)/(4) |
|
Answer» `(2x)/(3) + (3)/(2x) - (1)/(2)`  `:. sqrt((x^(2))/(9) + (9)/(4x^(2)) - (x)/(3) - (3)/(2x) = (5)/(4)) = (x)/(3) - (1)/(2) + (3)/(2x)` |
|
| 435. |
Rs 16,820 is divided between Govind and Geeta, both aged 27 and 25 years respectively. Their money is invested at 5% per annum compound interst in such a way that both receive equal to money at the age of 40 years. Find the share of each out of Rs 16,820. |
|
Answer» |
|
| 436. |
State the degree of each the following polynomials : sqrt(2)x^(2) -5x^(3) + 7x +(1)/(4) |
|
Answer» |
|
| 437. |
The sides containing right angles of a right angled triangle are 8 cm and 6 cm. It is rotated about its hypotenus. Find the volume and total surface area of the formed solid. |
|
Answer» |
|
| 438. |
The volume of a cylinder is 308 cm ^(3) . Its heights is 8cm . Find its lateral surface area and total surface area. |
|
Answer» |
|
| 440. |
If A={:[(8,-4),(12,4)]:},B={:[(12,-8),(8,8)]:}andC={:[(4,8),(4,8)]:}, then show that AC=BC. |
| Answer» | |
| 442. |
Divide the polynomial 2x ^(4) - 4x ^(3) - 3x -1 by (x-1) and find its quotient and remainder. |
|
Answer» |
|
| 443. |
Evaluate : (i) sin^(2)30^(@)-2cos^(3)60^(@)+3tan^(4)45^(@) (ii) (cos0^(@)+sin45^(@)+sin30^(@))(sin90^(@)-cos45^(@)+cos60^(@)) |
|
Answer» (II) `1""3/4` |
|
| 444. |
At a Ramzan Mela, a stall keeper in one of the food stalls has a large cylindrical vessel of base radius 15 cm filled up to a height of 32 cm with orange juice. The juice is filled in small cylindrical glasses (see the given figure) of radius 3 cm up to a height of 8 cm and sold for Rs. 3 each. How much money does the stall keeper receive by selling the juice completely ? |
|
Answer» |
|
| 445. |
In the givenfigure , ar (DRC) = ar ( DPC) and ar(BDP) = ar(ARC) . Showthat boththe quadrillaterals ABCDand DCPRare trapeziums. |
|
Answer» |
|
| 446. |
If a point C lies between two points A and B such that AC = BC, then prove that AC=(1)/(2)AB. Explain by drawing the figure. |
|
Answer» Solution :We have, AC = BC, Adding AC on both sides, we get `AC+AC=BC+AC"(if EQUALS ADDED to equals then wholes are equal)"` `rArr""2AC=AB""(becauseAC+CB=AB)` `rArr""AC=(1)/(2)AB"Hence Proved."` |
|
| 447. |
State the coefficient of x^(2) in each of the following polynomials : sqrt(2)x^(2) + 7x - 4sqrt(2) |
|
Answer» |
|
| 448. |
Given that angleA and angleB are supplementary angles. If angleA:angleB=7:8, then find angleA and angleB. |
|
Answer» |
|
| 449. |
Use suitable identities of find the following products (y^2+3/2)(y^2-3/2) |
|
Answer» |
|
| 450. |
Evaluate each of the following using proper identity : 82 xx 85 |
|
Answer» |
|