Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 451. |
The radius and height of a cylindrical cistern are 1.4 m and 2 m respectively. How many litres of water can it hold ? |
|
Answer» |
|
| 452. |
In the given figure, angle B lt angle A and angle C lt angle D. Show that AD lt BC. |
|
Answer» |
|
| 453. |
Find the total surface area of a hemisphere of radius 10 cm. (Use pi=3.14) |
|
Answer» |
|
| 454. |
piis |
|
Answer» a non-ALGEBRIC irrational number |
|
| 455. |
Evaluate each of the following using proper identity : (41)^(3) |
|
Answer» |
|
| 456. |
A is the centre of the circle and ABCD is a square. IfBD = 4cm then findthe radius of the circle |
|
Answer» |
|
| 457. |
Write the answer of each the question: What is the name of horizontal line and vertical lines drawn to determine the position of any point in the cartesian plane ? |
|
Answer» |
|
| 458. |
Find the zero of the polynomial in each of the following cases : p(x) = 3x-2 |
|
Answer» |
|
| 459. |
Ravi borrowed Rs 15,000 at the rate of 15% per annum for 2 years under simple interest. As he could not repay the loan after two years, the money lander lender increased the rate of interest to 20% per annum for the further period. If Ravi wants to repay the entire amount at the end of a total period of 3 years and 4 months, then how much he has to pay. (in Rs.) |
|
Answer» 24500 `P=15,000, R=15%, T=2` `I = (15,000 xx 15 xx 2)/(100) = RS 4500` Case 2: For the REMAINING time period `P=15,000, R=20%, T=16` months `I = (15,000 xx 20 xx 16/12)/(100)` `RARR I=(15,000 xx 20 xx 16)/(1200) = Rs 4000`. `therefore` Total amount that Ravi has to pay =15,000 + 4500 + 400 = Rs 23,500 |
|
| 461. |
O is the centre of the circle. The value of x in the given diagram is. . . . . .. . . |
|
Answer» `100^(@)` |
|
| 462. |
In,a circle, with center O, angleAOB=20^(@),angleBOC=40^(@), arc BC = 4 cm. Then length of arc AB will be. . . . . . . .. |
| Answer» Answer :C | |
| 463. |
ABCD is a quadrilateral in which AD = BC and angle DAB = angle CBA (see the given figure).Prove that ( i ) triangle ABD = triangle BAC, ( ii) BD = AC and (iii) angle ABD = angle BAC |
|
Answer» |
|
| 464. |
One card is drawn from a well-shuffled deck of 52 cards. Find the probability of getting a spade. |
|
Answer» |
|
| 465. |
Show that of all line segments drawn from a given point not on a given line, the perpendicular line segment is the shortest. |
|
Answer» |
|
| 466. |
Find the sum on which the compound interest for 3 years at 10% per annum amounts to Rs 1,655 |
|
Answer» |
|
| 467. |
Construct trianglePQR in which QR=3.2 cm, PQ+PR=5.9 cm and angleR-angleQ=60^(@) |
|
Answer» SOLUTION :Step 1: Draw line segment `QR = 3.2 cm.` Step 2: Draw `bar(RX)`, such that `angleQRX = (90^(@)+(angleR-angleQ)/(2))=90^(@)+30^(@)=120^(@)`. Step 3: TAKING `Q` as the center and a radius equal to `5.9 cm` (PQ + PR), draw an arc intersecting `bar(RX)` at S. Step 4: Draw `RY`, such that `angleQRY=(angleR-angleQ)/(2) = 30^(@)`, intersecting `QS` at `T.` Step 6: Draw the PERPENDICULAR bisector of `bar(RT)` intersecting `bar(QS)` at `P.` Step 7: Join `P` and `R.` `PQR` is the required triangle. 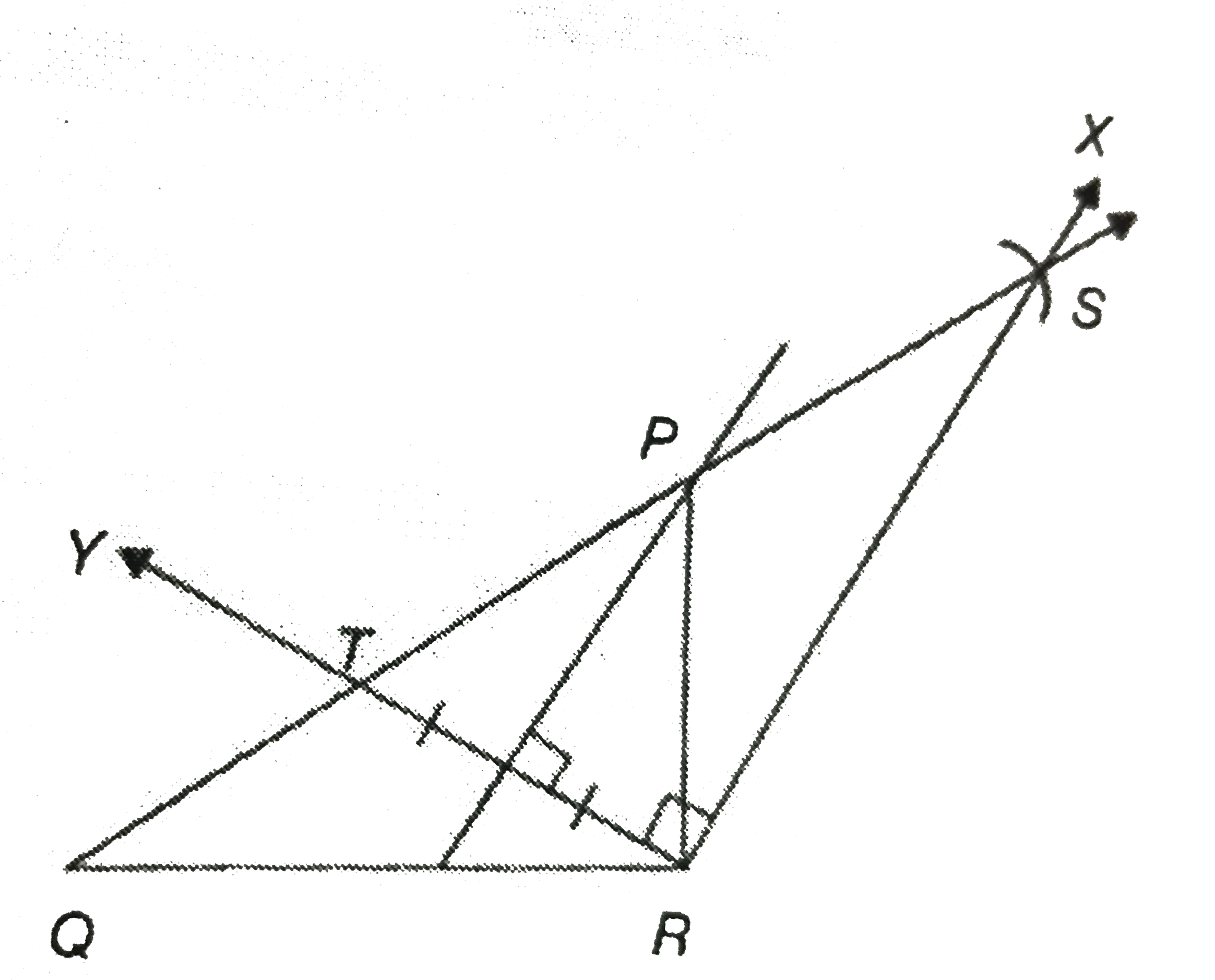
|
|
| 468. |
If 4cos^(2)x^(@)-1=0 and 0 le x^(@) le 90^(@), find : 1/(cos^(2)x^(@))-tan^(2)x^(@) |
|
Answer» |
|
| 469. |
Find the locus of the point P, such that TP : MP = 3 : 2, where T is (-2,3)and M is (4, -5). |
|
Answer» |
|
| 470. |
If (3,-2) is one of the solutions of kx-3y=21 , then k = ....... |
|
Answer» 3 |
|
| 471. |
The value of x from figure is. . . . . . . .. If 'O' is the centre of the circle |
|
Answer» 20 cm |
|
| 472. |
What is the empirical probability that an engineer lives : within 1/2 km from her place of work ? 12 |
|
Answer» |
|
| 473. |
Shanti Sweets Stall was placing an order for making cardboard boxes for packing their sweets. Two sizes of boxes were required. The bigger of dimensions 25 cm times 20 cm times 5 cm and the smaller of dimensions 15 cm times 12 cm times 5 cm. For all the overlaps, 5% of the total surface area is required extra. If the cost of the cardboard is Rs. 4 for 1000 cm^(2), find the cost of cardboard required for supplying 250 boxes of each kind. |
|
Answer» |
|
| 474. |
A sum of Rs 2500 is split into two parts, one part being lent at simple interest and the other part being lent at compound interest, interest being compounded annually. At the end of two years, the total amount of interest earned on the sum is Rs 201. Find the sum lent at simple interest, if both the part are lent at an interest rate of 4% per annum. |
|
Answer» Rs 1250 ii) `((2500-x)4 XX 2)/100+ x[(1+4/100)^(2)-1]=201` iii) Solve for `x`. |
|
| 475. |
A cubical box has each edge 10 cm and another cuboidal box is 12.5 cm long, 10 cm wide and 8 cm high. (i) Which box has the greater lateral surface area and by how much ? (ii) Which box has the smaller total surface area and by how much ? |
|
Answer» (ii) The total surface area of cubical box is smaller by 10 `cm^(2)` (610-600). |
|
| 476. |
Number of villages with respect to their population as per India census 2011 are given below. Find the average population in each village. |
|
Answer» |
|
| 477. |
A school wants to conduct tree plantation programme. For this a teacher allotted a circle of radius 6m ground to nineth standard students for plating sapplings. Four students plant trees at the points A,B,C and D as shown in figure. Here AB = 8m, CD = 10 m and AB bot CD. If another student places a flower pot at the point P, the intersection of AB and CD, then find the distance from the centre to P. |
|
Answer» |
|
| 478. |
Find the area of a triangle whose sides are 17 cm, 8 cm and 15 cm long. |
|
Answer» `75 cm^2` `:. " " s=(a+b+c)/(2) = (17+8+15)/(2) cm = 20 cm` By using Heron's formula, AREA `=SQRT(s(s-a)(s-b)(s-c))` `=sqrt(20(20-17)(20-8)(20-15))` `=sqrt(20xx3xx12xx5)` `=sqrt(4xx5xx3xx4xx3xx5)` `=4xx3xx5` `=60 cm^(2)` |
|
| 479. |
Draw a frequency polygon from the following data, giving the age of doctors working in C.G.H.S. in a city. |
Answer» Solution : The required frequency polygon is shown in the FOLLOWING figure: STEPS: 1. Draw a histogram for the given data. 2. Mark the mid-point at the top of each rectangle of the histogram drawn. 3. Also, mark the mid-point of the immediately lower class-interval (in the given EXAMPLE, the immediately lower class-interval is (20-25) and mid-point of the immediately HIGHER class-interval (in the given example the immediate upper class-interval is 50-55) 4. Join the consecutive mid-points marked by straight lines to OBTAIN the required frequency polygon. |
|
| 480. |
In the given figure, angle BCD = 43 ^(@) and angle BAE = 62 ^(@). Find the values of a,b,c and d. |
|
Answer» |
|
| 481. |
If all the four sides of a parallelogram are equal and the adjacent angles are of 120^(@) and 60^(@) then the name of the quadrilateral is. . . . . . . . . |
|
Answer» rectangle |
|
| 482. |
what is the total amount on which interest is paid till 1-8-2006 |
|
Answer» RS 160000 |
|
| 483. |
Locate the number 3.26 on the number line by the methodof successive magnification (Giveonly the signsof construction, description is not necessary ) . |
| Answer» | |
| 484. |
In triangleABC, AB = 4 holds good. |
| Answer» Answer :A::C | |
| 485. |
Evaluate each of the following using suitable identities : (104)^(3) |
|
Answer» |
|
| 486. |
Which of the following can be filledin a decision box? |
|
Answer» A,B,C `therefore` (A).(C ) and (D) CAB be filled in a decision box `because` answer for (b) cannot be yes or no |
|
| 490. |
Construct a DeltaABC in which BC = 8cm, angleB = 45^(@) and AB - AC = 3.5 cm. |
|
Answer» Solution :Given that, in `DeltaABC`, `BC = 8 cm,` `angleB = 45^(@)` and `AB - AC = 3.5 cm` Steps of construction : 1. Draw the base `BC = 8 cm` 2. At the point `B` make an `angleXBC = 45^(@)`. 3. Cut the LINE segment `BD` equal to `AB - AC` = `3.5 cm` from the ray `BX.` 4. Join `DC.` 5. Draw the perpendicular bisector, say `PQ` of `DC.` Let it INTERSECT `BX` at a point`A.` 7. Join `AC.` 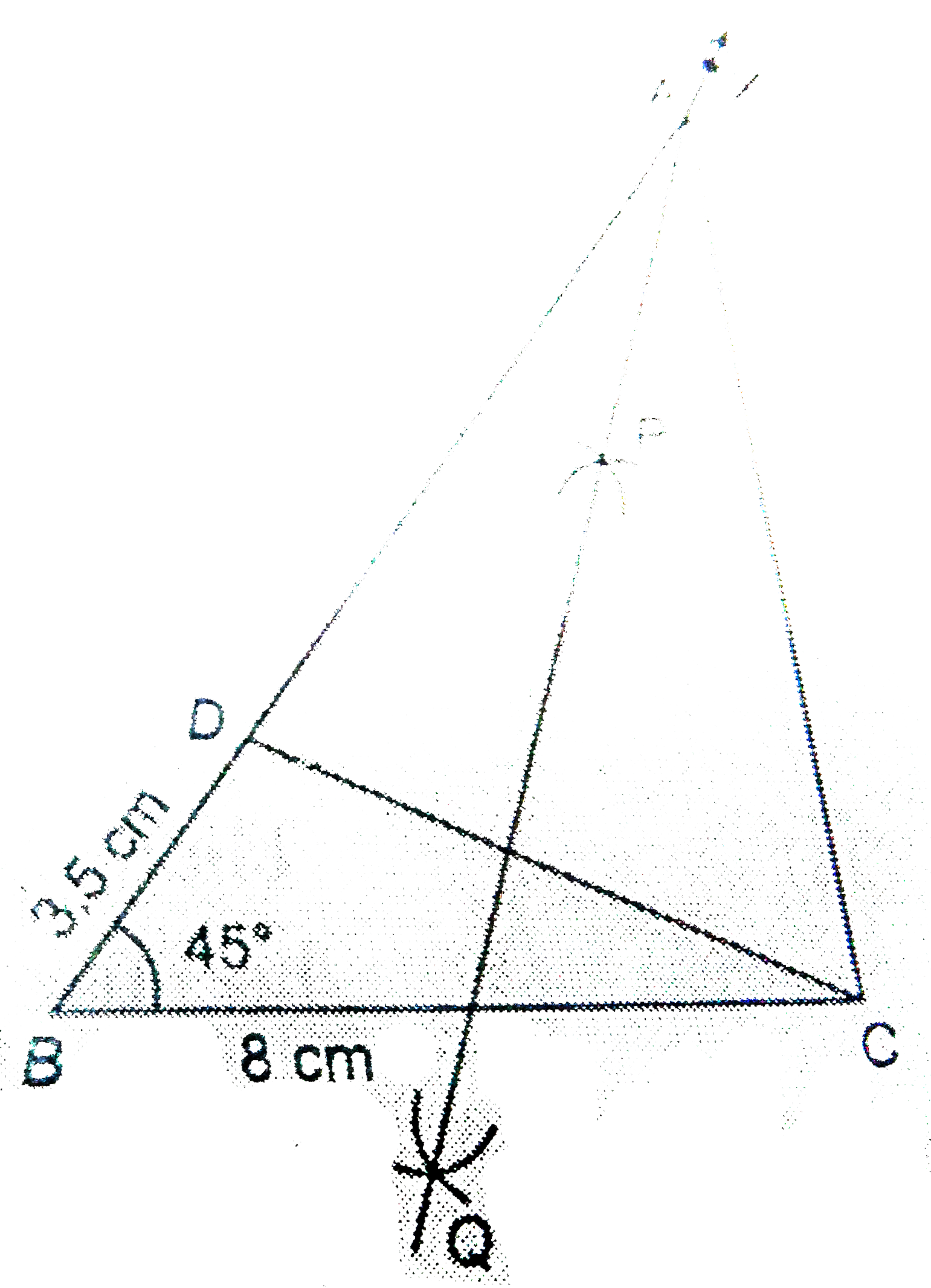
|
|
| 491. |
State which of the following expressions are a polynomial in one variable and which are not : 5x^(2) - 3x + 7 |
|
Answer» |
|
| 492. |
A sum is split into five equal parts. They are lent at annual rates of simple interests of 1%, 2%,3%, 10% and 5%. They are lent for 6 years, 4 years, 3 years, 1 year and 1 year, respectively. The simple interest on how many parts is at least 20% of the total interest? |
|
Answer» 1 ii) FIND the interest on each part. iii) Find the sum of the interest of 5 parts. Check which is GREATER than `20%` of the sum of INTERESTS. |
|
| 493. |
100 surnames were randomly picked up from a local telephone directory and a frequency distribution of the number of letter in English alphabet in the surnames was found as follows: (i) Draw a histogram to depict the given information. (ii) Write the class interval in which the maximum number of surnames lie. |
|
Answer» Solution :(i) We know that, the areas of the rectangles are proportional to the frequencies in a HISTOGRAM. Here, the widths of the rectangles are VARYING. So, we need to make certain modifications in the lengths of the rectangle. So that the areas are again proportional to the frequencies. 1 Select a class interval with the minimum class SIZE. The minimum class size is 2. 2. The lengths of the rectangles are then modified to be proportionate to the class-size 2. SINCE, we have calculated these lengths for interval of 2 letters in each case, we may call these lengths as 'proportion of surnames per 2 mark interval'. So, the correct histogram with varying width is given below: Here, we make a modified table by given data with minimum class-size 2 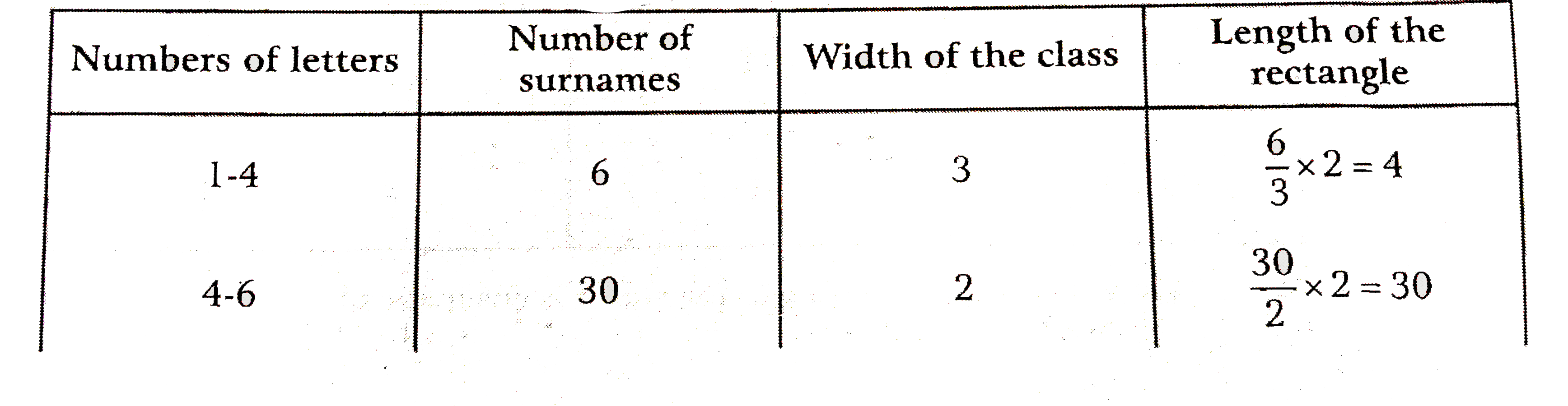 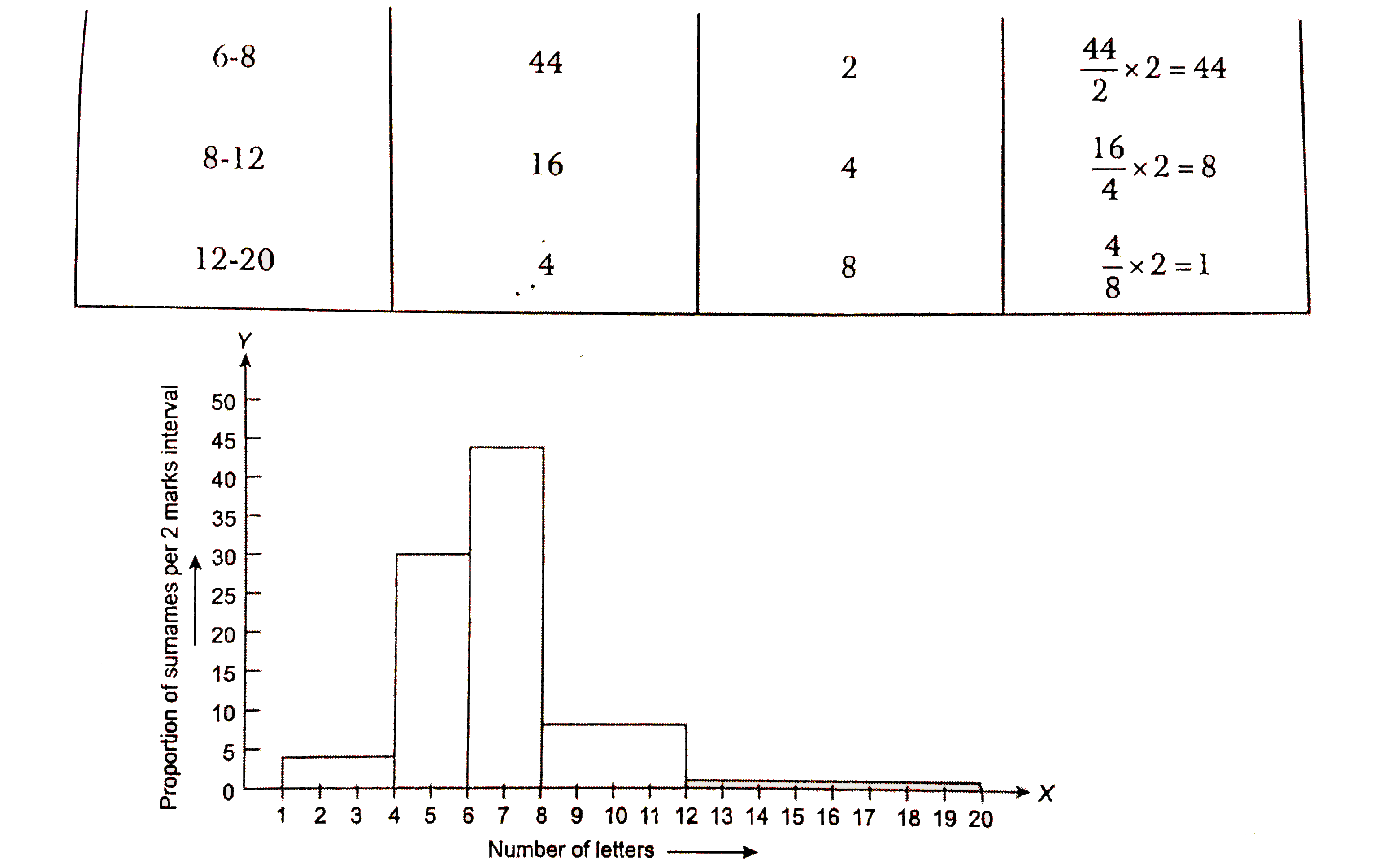 (ii) The class interval in which the maximum number of surnames lie is 6-8. |
|
| 494. |
Classify the following polynomials into linear quadratic and cubic polynomials : 27z^(3) |
|
Answer» |
|
| 496. |
Prove that an equilateral triangle can be constracted on any given line segment |
Answer» Solution :Let AB be the line segment of give LENGTH with A as CENTRE and AB as the radius DRAW a circle with B as centre and BA as the radius draw another circle CUTTING the first circle at C . Join AC and BC to form `triangle ABC` 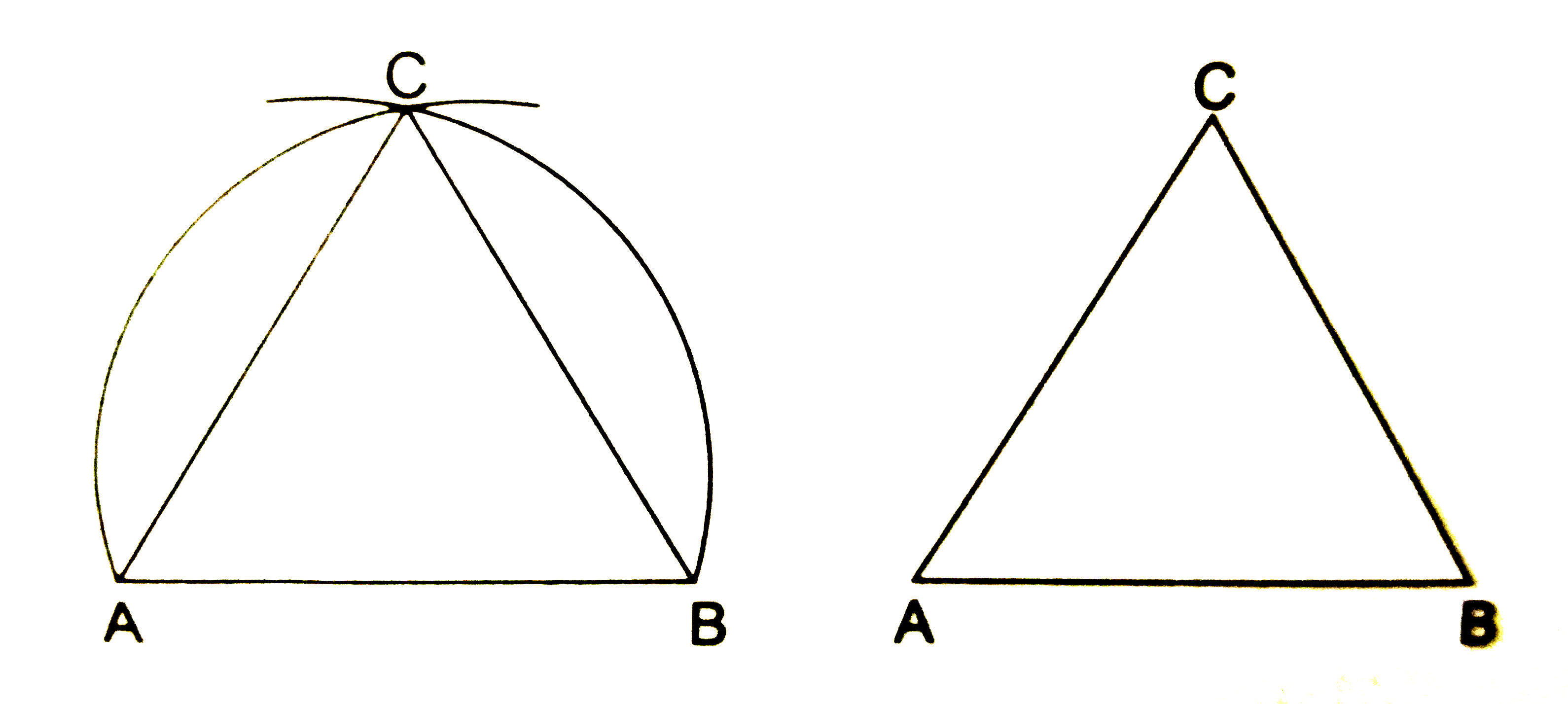 Now AB=AC(radii of the same circle) And BA =BC(radii of the same circle) `therefore` AB=BC`[therefore bar(BA)=bar(AB)]` But by Euclid 's Axiom 1 it follows that the things which are equal to the same things are equal to one another `therefore` AB=BC=AC Hence `triangle` ABC is an equilateral triangle |
|
| 497. |
A triangle if its perimeter is 10.4cm and two angles are 45^(@) and 120^(@) . |
|
Answer» Solution :Let `ABC` be a triangle. Then, given perimeter = `10.4 CM` i.e., `AB + BC + CA = 10.4cm` and two angles are `45^(@) and 120^(@)` . say `angleB = 45^(@) and ANGLEC = 120^(@)` Now, to construct the `Delta ABC` use the FOLLOWING steps. (i) Draw a line segment say XY and equal to perimeter i.e., `AB + BC + CA = 10.4cm` (ii) Make angle `angleLXY = angleB = 45^(@) and angleMYX = angleC = 120^(@)`. (III) Bisect `angleLXYand angleMYX` and let these bisectors intersect at a point A (say). 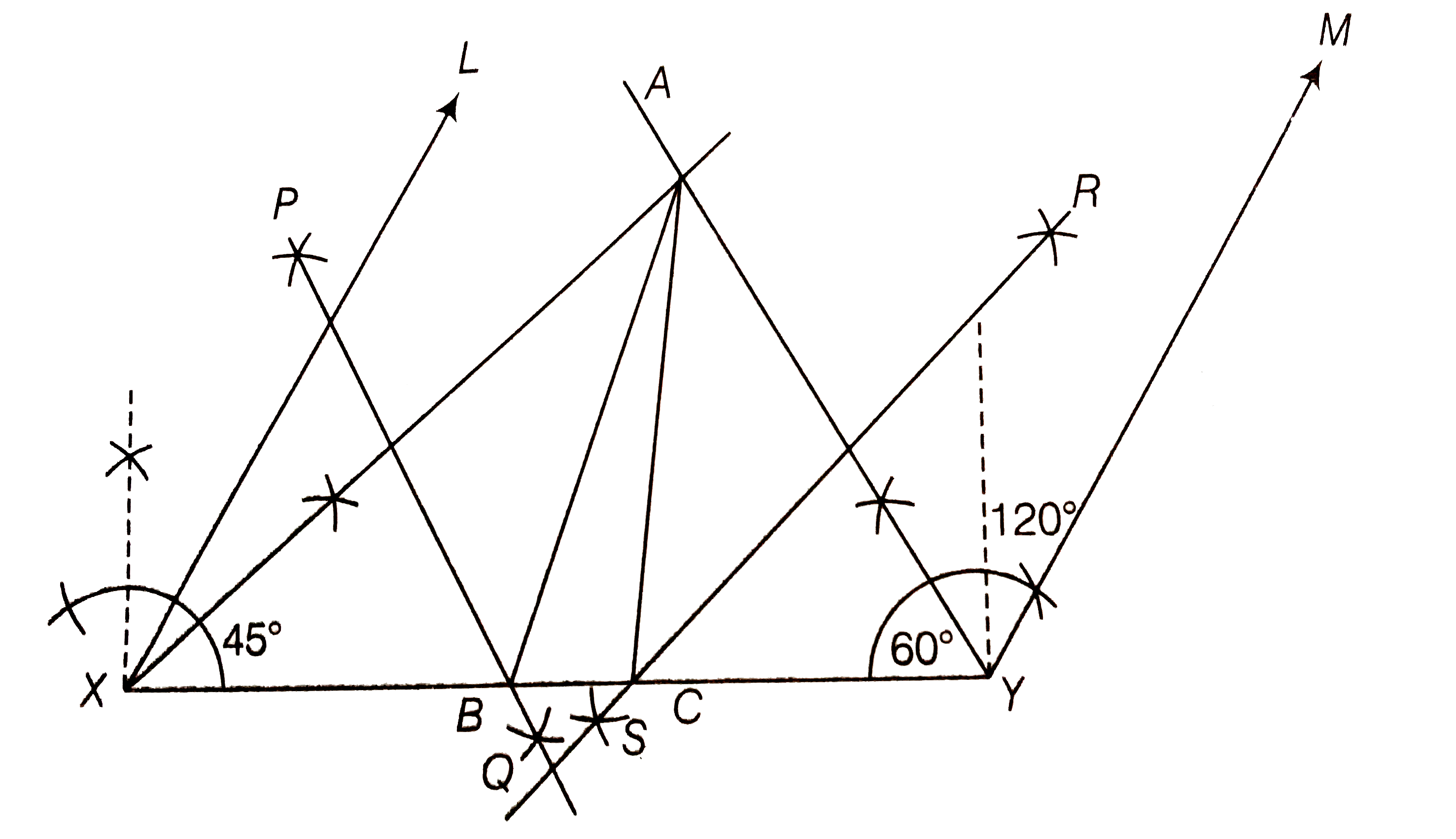 (iv) Draw perpendicular bisectors PQ and RS of AX and AY, respectively. (v) Let PQ intersect XY at B and RS intersect XY at C. Join AB and AC. Thus , `DELTAABC` is the required triangle. JustificationSince, B lies on the perpendicular bisector PQ of AX. `:.`XB = AB Since, C lies on the perpendicular bisector RS of AY. `:.`CY = AC Thus, `AB + BC + CA = XB + CY = XY` Again, `angleBAX = angleAXB` [`because` in `DeltaAXB`, AB = XB]....(i) Also,`angleABC = angleBAX + angleAXB` [`because angleABC` is an exterior angle of `DeltaAXB`] = `angle AXB + angleAXB` [from Eq. (i)] = `2 angleAXB= angleLXY`[`because` AX is a bisector of `angleLXB`] Also,`angleCAY = angleAYC` [`because in DeltaAYC`, AC = CY] `:. angleACB = angleCAY + angleAYC` [`because angle ACB` is an exterior angle of `DeltaAYC`] = `angleCAY + angleCAY` = `2 angleCAY = angleMYX` [`because` AY is a bisector of `angleMYX`] Thus, our construction is justified. |
|
| 498. |
Bala opened a saving bank account with a bank on 4-1-2007 where interest is credited at the year end. The sum of the minimum balance held by bala up to the end of december 2007 was rs 4800 he earned an interest of Rs 2 month that year find the annual rate of interest |
|
Answer» 6% per annum TOTAL interest for that year (in RS ) =(2)(12)=24 `24=((4800)(R ))/((100)(12)) R=6% |
|
| 499. |
Write the answer of each the question: What is the name fo each part of the plane formed by these two lines ? |
|
Answer» |
|