|
Answer» In a HYPOTHETICAL system , a partical of mass `m` and charge `-3 q` is moving around a very heavy partical chaRGE `q`. Assume that Bohr's model is applicable to this system , then velocuity of mass `m` in the first orbit is `(3 q^(2))/(2 epsilon_(0) h)` `(3 q^(2))/(4 epsilon_(0) h)` `(3 q)/(2 pi epsilon_(0) h)` `(3 q^(2))/(4 pi epsilon_(0) h)` A `(mv^(2))/( r) = (3 q^(3))/(4 pi epsilon_(0) r^(2)) implies m v r = (3 q^(2))/(4 pi epsilon_(0) v)` (i)
and `(nh)/(2 pi) = m v r` (ii)
Using Bohr's (i) and (ii) and putting `n = 1`
`(h)/(2 pi) = (3 q^(2))/(4 pi epsilon_(0) v) implies v = (3 q^(2))/(2 pi epsilon_(0) h)`The binding energy of nucei X and `Y` are `E_(1)` and `E_(2)`, respectively. Two atoms of X fuse to give one atom of `Y` and an energy `Q` is released. Then, `Q=2E_(1) -E_(2)` `Q=2E_(2)-2E_(1)` `Qlt2E_(1) -E_(2)` `Q gt2E_(2) -2E_(1)` b During fusion, binding energy of daughter nucleus is always greater than the total binding energy of the parent nuclei. The difference of binding energied is released. Hence,
`Q=E_(2) -2E_(1)`.A boy is trying to start a fire by focusing sunlight on a piece of paper using an equiconvex lens of focal length `10cm`. The diameter of the sun is `1.39xx10^(9)m` and its mean distance from the earth is `1.5xx10^(11)m`. What is the diameter of the sun's image on the paper ? `9.2xx10^(-4)m` `6.5xx10^(-4)m` `6.5xx10^(-5)m` `12.4xx10^(-4)m` A From the relation `(I)/(O)=(v)/(u)`
Here, `O=1.39xx10^(9),v=0.1m`,
`u=1.5xx10^(11)m`
`:. I=(0.1)/(1.5xx10^(11))xx1.39xx10^(9)=9.2xx10^(-4)m`The temperature of an open room of volume `30 m^(3)` increases from `17^(@)C to 27^(@)C` due to sunshine. The atmospheric pressure in the room remains `1 xx 10^(5) Pa`. If `n_(i) and n_(f)` are the number of molecules in the room before and after heating then `n_(f)` and `n_(i)` will be `2.5 xx 10^(25)` `-2.5 xx 10^(25)` `-1.61 xx 10^(23)` `1.38 xx 10^(23)` B Here, `V_(1) = 30m^(3), T_(1) = 17+273 = 290 K`
`P_(1) = 1 xx 10^(5)Pa`
`V_(2) = 30 m^(3) , T_(2) = 27+273 = 300K`,
`P_(2) = 1 xx 10^(5) Pa`.
Let `N_(1),N_(2)` be the no, of moles of a gas at temperature `T_(1) and T_(2)` respectively. then
`N_(1) =(P_(1)V_(1))/(RT_(1)) = ((1 xx 10^(5)) xx 30)/(83 xx 290) = 1.24 xx 10^(3)`
or `N_(2) = (P_(2)V_(2))/(RT_(2)) = ((1 xx 10^(5)) xx 30)/(83 xx 300) = 1.20 xx 10^(3)` ltbr. Change in the number of moles
`N_(2)-N_(1) =(1.20-1.24) xx 10^(3) = -0.04 xx 10^(3)`
Change in the number of molecules
`n_(f)-n_(i) = (N_(2)-N_(1)) xx (6.023 xx 10^(23))`
`= - (0.04 xx 10^(3)) xx (6.023 xx 10^(23))`
`=-2.5 xx 10^(25)`.An ideal monoatomic gas is confined in a horizontal cylinder by a spring loaded piston (as shown in the Fig.) Initially, the gas is at temperature `T_(1), pressure P_(1) and volume V_(1)` and the spring is in its relaxed state. The gas is then heated very slowly to `temperature T_(2), pressure P_(2) and volume V_(2)`. during this process, the piston moves out by a distance x. ignoring the friction between the piston and the cylinder, the correct statement(s) is (are)
 If `V_(2) = 2V_(1) and T_(2)=3T_(1)`, then the energy stored in the string is `1/4 P_(1)V_(1)` If `V_(2) and 2V_(1)` and `T_(2) = 3T_(1)`, then the charge in iternal energy is `3P_(1)V_(1)`. If `V_(2)=3V_(1)` and `T_(2) = 4T_(1)`, then the work done by the gas is `7/3 P_(1)V_(1)` If `V_(2) = 3V_(1)` and `T_(2) = 4T_(1)`, then the heat supplied to the gas is `17/6 P_(1)V_(1)`. B From gas equation , `(P_(1)V_(1))/(T_1) = (P_(2)V_(2))/(T_2) = nR or P_(2) = (P_(1)V_(1)T_(2))/(V_(2)T_(1)) ` ...(i) If `V_(2) = 2V_(1) and T_(2)=3T_(1)`, then the energy stored in the string is `1/4 P_(1)V_(1)` If `V_(2) and 2V_(1)` and `T_(2) = 3T_(1)`, then the charge in iternal energy is `3P_(1)V_(1)`. If `V_(2)=3V_(1)` and `T_(2) = 4T_(1)`, then the work done by the gas is `7/3 P_(1)V_(1)` If `V_(2) = 3V_(1)` and `T_(2) = 4T_(1)`, then the heat supplied to the gas is `17/6 P_(1)V_(1)`. B From gas equation , `(P_(1)V_(1))/(T_1) = (P_(2)V_(2))/(T_2) = nR or P_(2) = (P_(1)V_(1)T_(2))/(V_(2)T_(1)) ` ...(i)
(a) when `V_(2) = 2 V_(1), T_(2) = 3T_(1)`, then
`P_(2) = (P_(1)V_(1) xx 3T_(1))/(2 V_(1) xx T_(1)) = 3/2 P_(1)`
If A is the area of cross- section of the piston, then
`P_(2)A = kx or P_(2)Ax = kx^(2)`
Energy in spring , `U = 1/2 kx^(2) = 1/2 P_(2) Ax`
`=1/2 P_(2)(V_(2)-V_(1))`
`=1/2 xx (3P_1)/(2) (2V_(1)-V_(1)) = 3/4 P_(1)V_(1)`
Thus, option (a) is wrong.
(b) When `V_(2) = 2V_(1) and T_(2) = 3T_(1) , P_(2) = 3/2P_(1)` [from (i) ]
Change in internal energy ,
`dU = nC_(v) dT = m((3R)/(2)) (T_(2)-T_(1))`
`= n xx (3R)/(2) [3T_(1)-T_(1)] = 3nRT_(1) = 3P_(1)V_(1)`
Thus option (b) is true.
(c) when `V_(2) = 3V_(1) and T_(2) = 4T_(1)`
`P_(2) = (P_(1)V_(1)xx4T_(1))/(3V_(1)xxT_(1)) = 4/2 P_(1)`
Workdone , dW = energy in spring
`1/2kx^(2) = 1/2 P_(2)(V_(2)-V_(1))`
`1/2 xx 4/3 P_(1)[3V_(1)-C_(1)] = 4/3 P_(1)V_(1)`
Thus option (c) is wrong.
(d) when `V_(2) = 3V_(1) and T_(2) = 4T_(1), P_(2) = 4/3 P_(1)`
Heat supplied to the gas, `dQ = dU + dW`
`dQ = n xx (3R)/(2)[T_(2)-T_(1)]+1/2 P_(2)(V_(2)-V_(1))`
`=3/2 nR [4T_(1)-T_(1)] + 1/2 4/3 P_(1)[3V_(1)-V_(1)]`
`= 9/2 nRT_(1)+4/2 P_(1)V_(1) = 9/2 P_(1)V_(1)+ 4/2 P_(1)V_(1) = 35/6 P_(1)V_(1)`.
Thus, option (d) is wrong.Two rigid boxes containing different ideal gases are placed on a table. Box A contains one mole of nitrogen at `T_(0)`, while box B contains one mole of He at `7//3 T_(0)`. The boxes are then put into thermal contact with eachother, and heat flows between them till the gases reach a common final temperature `T_(f)`. ignore the heat capacity of boxes. then `T_(f) "in terms of" T_(0)` is `T_(f) = (7)/(3)T_(0)` `T_(f) = (3)/(2)T_(0)` `T_(f) = (5)/(2)T_(0)` `T_(f) = (3)/(7)T_(0)` B Here, `n_(1) "mole" , n_(2) = 1 "mole"`
For nitrogen, `C_(p_1)=7/2 R`
for helium, `C_(p_2) = 5/2 R`
`T_(1)=T_(0), T_(2) = 7/3 T_(0).T_(f)=?`
when gases are put into thermal contact, heat is exchanged between them till final temperature `T_(f)` is reached.
Heat gained by nitrogen = Heat lost by He
`n_(1)C_(P_1)(T_(f)-T_(1)) = n_(2)C_(P_2) (T_(2)-T_(f))`
`(n_(1)C_(P_1)+n_(2)C_(p_2)) T_(f) = n_(2)C_(p_2) T_(2) n_(1)C_(p_1)T_(1)`
`(1 xx 7.2 R + 5/2 R) T_(f) = 1 xx 5/2 R xx 7/3 T_(0) + 1 xx 7/2 RT_(0)`
`6RT_(f) = (35/6 + 7/2)RT_(0)`
`T_(f) = (56)/(6 xx 6) T_(0)~~3/2 T_(0)`.If by mistake Ammeter is connected parallel to the resistance then `i-V` curve expected is (Here `i`= reading of ammeter, `V=` reading of voltmeter)
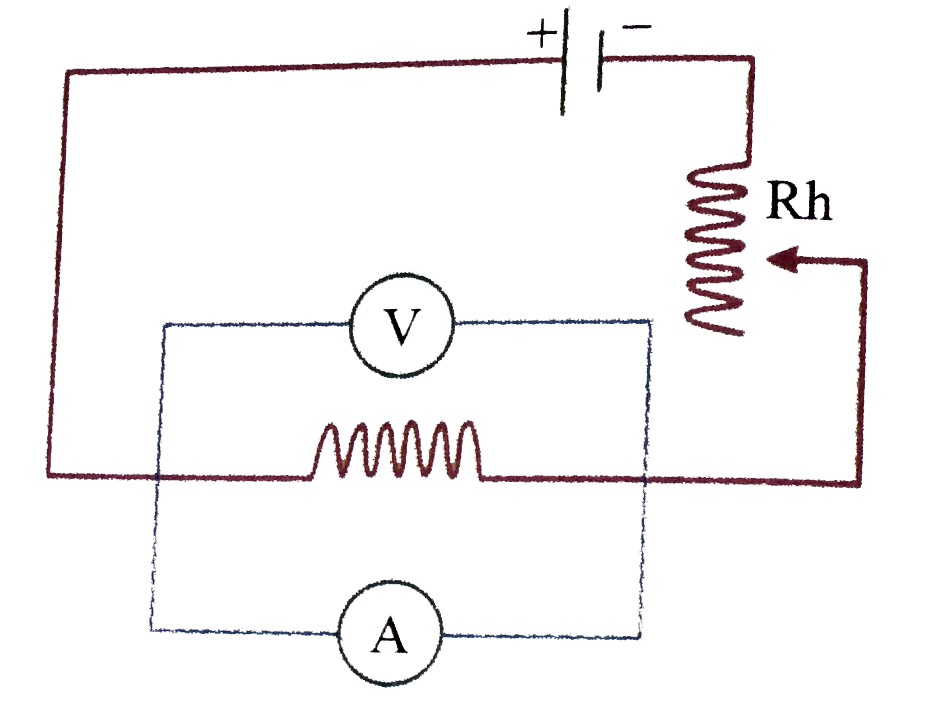 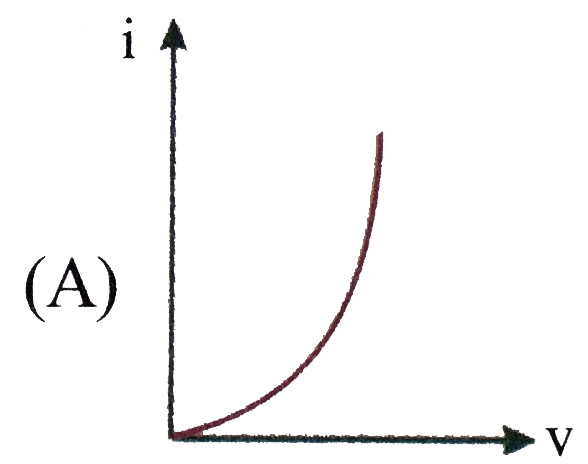  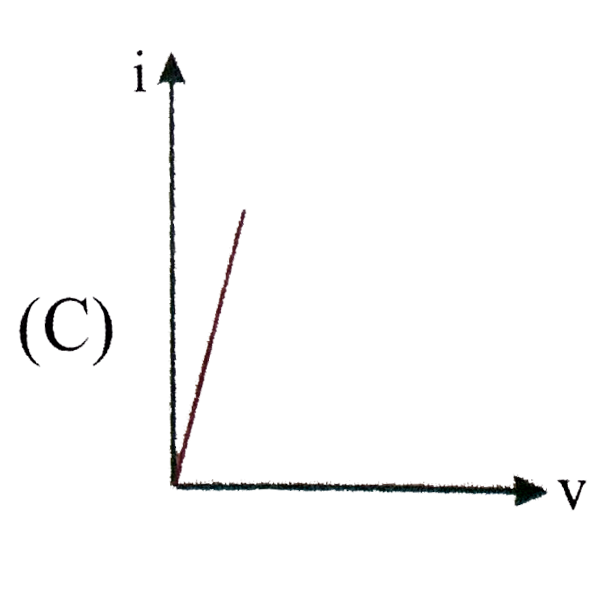  C As ammeter has very low resistance most of current will pass through the ammeter so reading of ammeter (`i`) will be very large. Voltmeter has very high resistance so reading of voltmeter will be very low.Unit of `(CV)/(rho epsilon_(0))` are of C As ammeter has very low resistance most of current will pass through the ammeter so reading of ammeter (`i`) will be very large. Voltmeter has very high resistance so reading of voltmeter will be very low.Unit of `(CV)/(rho epsilon_(0))` are of
(`C =` capacitance, `V =` potential, `rho =` specfic resistence and `epsilon_(0) =` permittivity of free space) Charge current time frequency B `C = (epsilon_(0)A)/(d)` and `rho = (RA)/(l)`
Substituting in `(CV)/(rhoepsilon_(0))` we get
`(CV)/(rhoepsilon_(0))= (((epsilon_(0)A)/(d))(V))/((R (A)/(l)) epsilon_(0))-="current"`.Two separate monochromatic light beams `A` and `B` of the same intensity (energy per unit area per unit time) are falling normally on a unit area of a metallic surface. Their wavelength are `lambda_(A)` and `lambda_(B)` respectively. Assuming that all the the incident light is used in ejecting the photoelectrons, the ratio of the number of photoelectrons from beam `A` to that from `B` is `(lambda_(A)/lambda_(B))` `(lambda_(B)/lambda_(A))` `(lambda_(A)/lambda_(B))^(2)` `(lambda_(B)/lambda_(A))^(2)` A The number of photo electron depends on the Number of photons Number of photon `=I/(hc//lambda)=(lambda.I)/(hc) prop lambda`
Ratio of no. of photo electrons =`lambda_(A)/lambda_(B)`The de Broglie wavelength of an neutron corresponding to root mean square speed at `927^(@)` is `lambda`. What will be the de Broglie wavelength of the neutron corresponding to root mean square speed at `27^(@)C`? `(lambda)/(2)` `lambda` `2 lambda` `4 lambda` C `K.E.` of neutron `E=(3)/(2)KT`
`lambda_(d)=(h)/(p)=(h)/(sqrt(2mE))=(h)/(sqrt(2mxx(3)/(2)kT))`
`rArr lambda_(2)=lambdasqrt(((927+273))/(27+273))= 2 lambda`A uniform metal rod is used as a bar pendulum. If the room temperature rises by `10^(@)C` , and the coefficient of linear expansion of the metal of the rod is `2xx10^(-6)` per `.^(@)C` , the period of the pendulum will have percentage increase of `-2xx10^(-3)` `-1xx10^(-3)` `2xx10^(-3)` `1xx10^(-3)` DIf on heating throught `80^(@)C` , the mass expelled is `(1//100)^(th)` of mass still remaining, the coefficient of apparent expansion of liquid is `1.25xx10^(-4)//^(@)C` `12.5xx10^(-4)//^(@)C` `1.25xx10^(-5)//^(@)C` None of these ATwo identical containers A and B with frictionless pistons contain the same ideal gas at the same temperature and the same volume V . The mass of the gas in A is `m_(A)`and that in B is `m_(B).` The gas in each cylinder is now allowed to expand isothermally to the same final volume 2 V . The changes in the pressure in A and B are found to be `DeltaP`and 1.5 `DeltaP` respectively. Then `4m_(A)=9m_(B)` `2m_(A)=3m_(B)` `3m_(A)=2m_(B)` `9m_(A)=3m_(B)` CFollowing figure shows on adiabatic cylindrical container of volume `V_(0)` divided by an adiabatic smooth piston (area of cross-section = A ) in two equal parts. An ideal gas `(C_(p)//C_(y)=lambda)` is at pressure P and temperature T in left part and gas at pressure P and temperature T in right part. The piston is slowly displaced and released at a position where it can stay in equilibrium. The final pressure of the two parts will be (SUPPOSE x = displacement of the piston)
 `P_(2)` `P_(1)` `(P_(1)(V_(0)/(2))^(lambda))/((V_(0)/(2)+Ax)^(lambda))` `(P_(2)(V_(0)/(2))^(lambda))/((V_(0)/(2)+Ax)^(lambda))` CIn the FOLLOWING P-V diagram two adiabatics cut two isothermals at temperatures T and T (fig).The value of `(V_(a))/(V_(d))` will be `P_(2)` `P_(1)` `(P_(1)(V_(0)/(2))^(lambda))/((V_(0)/(2)+Ax)^(lambda))` `(P_(2)(V_(0)/(2))^(lambda))/((V_(0)/(2)+Ax)^(lambda))` CIn the FOLLOWING P-V diagram two adiabatics cut two isothermals at temperatures T and T (fig).The value of `(V_(a))/(V_(d))` will be
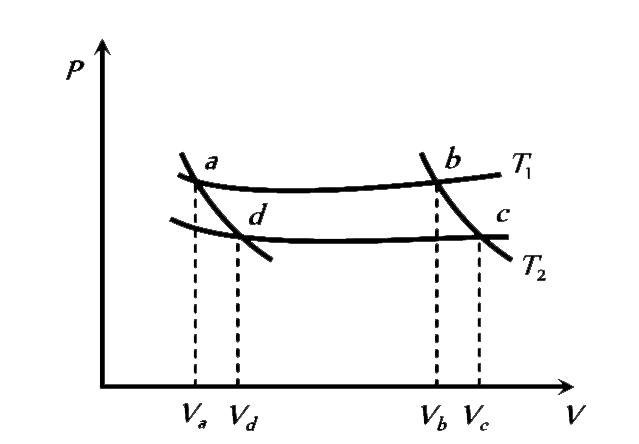 `(V_(b))/(V_(c))` `(V_(c))/(V_(b))` `(V_(d))/(V_(a))` `V_(b)V_(e)` AA light ray from air is incident (as shown in figure) at one end of a glass fiber (refractive index `mu = 1.5`) making an incidence angle of `60^(@)` on the lateral surface, so that it undergoes a total internal reflection. How much time would it TAKE to traverse the straight fiber of length 1 km `(V_(b))/(V_(c))` `(V_(c))/(V_(b))` `(V_(d))/(V_(a))` `V_(b)V_(e)` AA light ray from air is incident (as shown in figure) at one end of a glass fiber (refractive index `mu = 1.5`) making an incidence angle of `60^(@)` on the lateral surface, so that it undergoes a total internal reflection. How much time would it TAKE to traverse the straight fiber of length 1 km
 `3.33 mu sec` `6.67 mu sec` `5.77 mu sec` `3.85 mu sec` D N/AA combination of two thin lenses with focal lengths `f_(1)` and `f_(2)` respectively forms an image of distant object at distance 60 cm when lenses are in contact. The position of this image shifts by 30 cm towards the combination when two lenses are separated by 10 cm . The corresponding values of `f_(1)` and `f_(2)` are 30 cm, -60 cm 20 cm, -30 cm 15 cm, -20 cm 12 cm, -15 cm B N/AAn optical instrument uses a 25 D objective and 20 D eyepeice with a tube length of 25 cm when eye is least strained The instrument is a telescope with angular magnification 20. The instrument is a microscope with angular magnification 20. The instrument is a telescope with angular magnification 24. The instrument is a microscope with angular magnification 24. B N/AThe ratio of d-Brogile wavelength off mlecules of hydrogen and helium gas moving at arms speed in two gas jars kept sparately at temeperature `37^(@)` C and `127^(@)` C respectively is : `(2)/sqrt(3)` `sqrt(2/(3))` `sqrt(3)/(2)` `sqrt(8/(3)` DAt t=O, light of intensity `10^(12)` photons/` s-m^(2)` of energy 6eV per photon starts falling on a plate with work founction `2.5 eV` If area of the plate is `2xx10^(-4) m^(2)` and for every `10^(5)` photons one photoelectron is emitted, charge on the plate at t=25 s is `8xx10^(-15) C` `4xx10^(-14) C` `12xx10^(-10) C` `16xx10^(-12) C` ARadius of an electron moving in a circle in constant magnetic field is two times that of an `alpha` particle in the same field. Then de-Broglie wavelength of electrons is x-times of the `alpha`-particle Here x is1A telescope has an objective lens of `10cm` diameter and is situated at a distance of one kilometre from two objects. The minimum distance between these two objects, which can be resolved by the telescope, when the mean wavelength of light is `5000 Ã…`, of the order of mm is :5 Resolving limit of telescope is `3.33 mu sec` `6.67 mu sec` `5.77 mu sec` `3.85 mu sec` D N/AA combination of two thin lenses with focal lengths `f_(1)` and `f_(2)` respectively forms an image of distant object at distance 60 cm when lenses are in contact. The position of this image shifts by 30 cm towards the combination when two lenses are separated by 10 cm . The corresponding values of `f_(1)` and `f_(2)` are 30 cm, -60 cm 20 cm, -30 cm 15 cm, -20 cm 12 cm, -15 cm B N/AAn optical instrument uses a 25 D objective and 20 D eyepeice with a tube length of 25 cm when eye is least strained The instrument is a telescope with angular magnification 20. The instrument is a microscope with angular magnification 20. The instrument is a telescope with angular magnification 24. The instrument is a microscope with angular magnification 24. B N/AThe ratio of d-Brogile wavelength off mlecules of hydrogen and helium gas moving at arms speed in two gas jars kept sparately at temeperature `37^(@)` C and `127^(@)` C respectively is : `(2)/sqrt(3)` `sqrt(2/(3))` `sqrt(3)/(2)` `sqrt(8/(3)` DAt t=O, light of intensity `10^(12)` photons/` s-m^(2)` of energy 6eV per photon starts falling on a plate with work founction `2.5 eV` If area of the plate is `2xx10^(-4) m^(2)` and for every `10^(5)` photons one photoelectron is emitted, charge on the plate at t=25 s is `8xx10^(-15) C` `4xx10^(-14) C` `12xx10^(-10) C` `16xx10^(-12) C` ARadius of an electron moving in a circle in constant magnetic field is two times that of an `alpha` particle in the same field. Then de-Broglie wavelength of electrons is x-times of the `alpha`-particle Here x is1A telescope has an objective lens of `10cm` diameter and is situated at a distance of one kilometre from two objects. The minimum distance between these two objects, which can be resolved by the telescope, when the mean wavelength of light is `5000 Ã…`, of the order of mm is :5 Resolving limit of telescope is
`theta prop (x)/(D)=(lambda)/(d)implies x=(lambdaD)/(d)`
Given, `lambda=5000 Ã…=5000xx10^(-1)m`
`D=1km=1000m`
`d=10cm=0.1m`
Hence, `x=(5000xx10^(-10)xx1000)/(0.1)`
`=5xx10^(-3)m=5mm`A spring is placed between the jaws of screw gauge such that the spring is not all compressed. The mai scale reads 2 division and circular scale reads 28 divisions. Now we turn the circular scale by `18^(@)` such that the spring is compessed. The circular scale has 200 divisions and the least count of the main scale is `1mm`. the force exerted by the spring on the jaws in unit `mN`. (the spring constnat is `100N//m`)5Assuming human pupil to have a radius of 0.25 cm and a comfortable viewing distance of 25 cm, the minimum separation between two objects than human eye can resolve at 500nm wavelength is `X mm` , so value of `x` is:30
`sintheta=(0.25)/(25)=(1)/(100)`
Resolving power `=(1.22lamda)/(2musintheta)=30mum`In a cyclic process shown in the figure an ideal gas is adiabatically taken from `B` and `A`, the work done on the gas during the process `B rarr A` is `30 J`, when the gas is taken from `A rarr B` the heat absorbed by the gas is `20 J`. The change in internal energy of the gas in the process `A rarr B` is given as `-X`, so value of `X` is - :
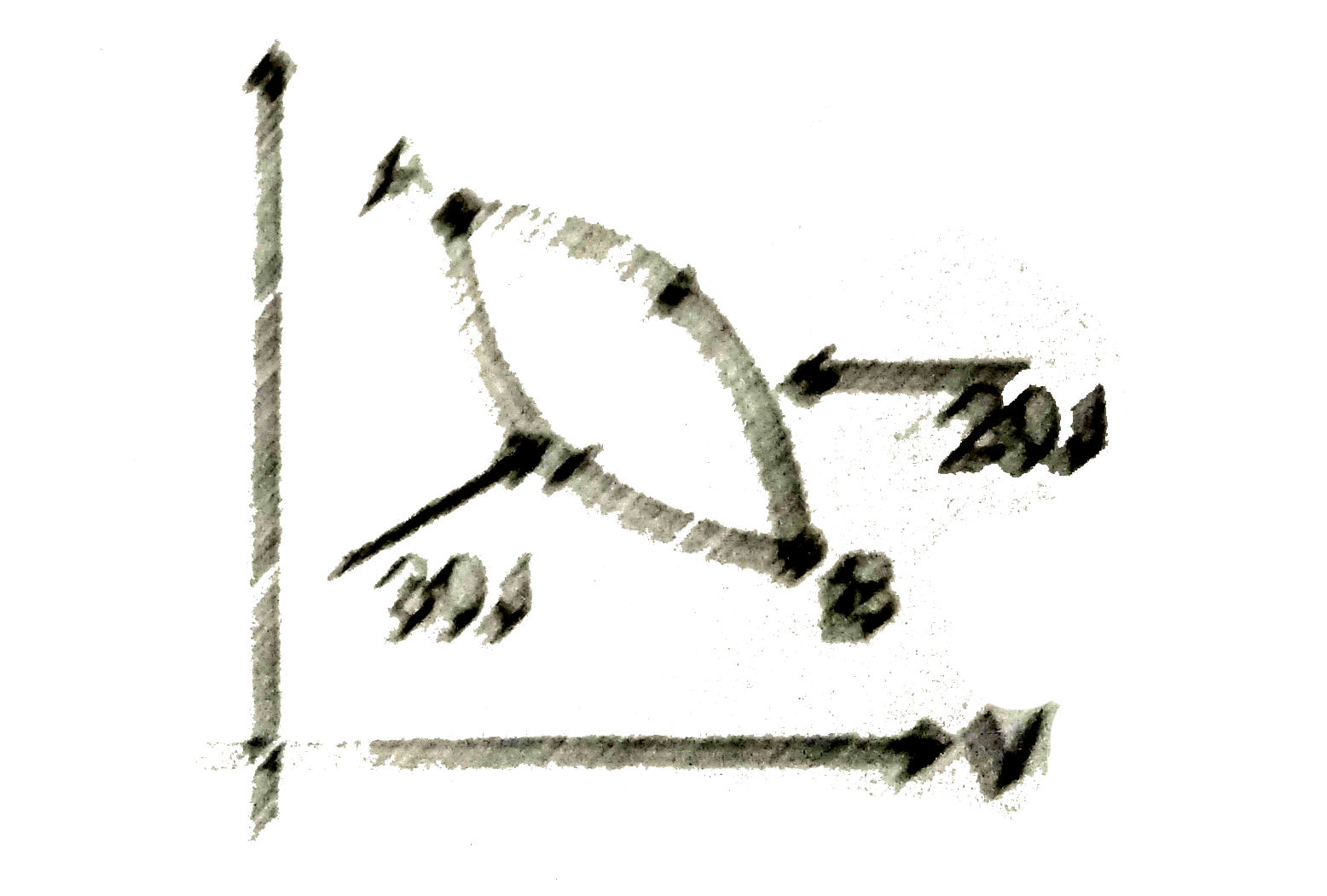 30 N//A 30 N//A Solution :The time taken by the ultrasonic sound waves to travel from the ship to the sea-bed, and back to the ship is 4 seconds. So, the time taken by the ultrasonic sound to travel from the ship to sea-bed will be half of this time, which is `(4)/(2) =2` second. This means that the sound takes 2 seconds to travel from the ship to the bottom of the sea.
Now, Speed `= ("Distance")/("Time")`
So, `1500 = ("Distance")/(2)`
And, Distance `= 1500 xx 2m = 3000m`
Thus, the depth of this sea below the ship is 3000 METRES.
|
 If `V_(2) = 2V_(1) and T_(2)=3T_(1)`, then the energy stored in the string is `1/4 P_(1)V_(1)` If `V_(2) and 2V_(1)` and `T_(2) = 3T_(1)`, then the charge in iternal energy is `3P_(1)V_(1)`. If `V_(2)=3V_(1)` and `T_(2) = 4T_(1)`, then the work done by the gas is `7/3 P_(1)V_(1)` If `V_(2) = 3V_(1)` and `T_(2) = 4T_(1)`, then the heat supplied to the gas is `17/6 P_(1)V_(1)`. B From gas equation , `(P_(1)V_(1))/(T_1) = (P_(2)V_(2))/(T_2) = nR or P_(2) = (P_(1)V_(1)T_(2))/(V_(2)T_(1)) ` ...(i)
If `V_(2) = 2V_(1) and T_(2)=3T_(1)`, then the energy stored in the string is `1/4 P_(1)V_(1)` If `V_(2) and 2V_(1)` and `T_(2) = 3T_(1)`, then the charge in iternal energy is `3P_(1)V_(1)`. If `V_(2)=3V_(1)` and `T_(2) = 4T_(1)`, then the work done by the gas is `7/3 P_(1)V_(1)` If `V_(2) = 3V_(1)` and `T_(2) = 4T_(1)`, then the heat supplied to the gas is `17/6 P_(1)V_(1)`. B From gas equation , `(P_(1)V_(1))/(T_1) = (P_(2)V_(2))/(T_2) = nR or P_(2) = (P_(1)V_(1)T_(2))/(V_(2)T_(1)) ` ...(i) 



 C As ammeter has very low resistance most of current will pass through the ammeter so reading of ammeter (`i`) will be very large. Voltmeter has very high resistance so reading of voltmeter will be very low.Unit of `(CV)/(rho epsilon_(0))` are of
C As ammeter has very low resistance most of current will pass through the ammeter so reading of ammeter (`i`) will be very large. Voltmeter has very high resistance so reading of voltmeter will be very low.Unit of `(CV)/(rho epsilon_(0))` are of  `P_(2)` `P_(1)` `(P_(1)(V_(0)/(2))^(lambda))/((V_(0)/(2)+Ax)^(lambda))` `(P_(2)(V_(0)/(2))^(lambda))/((V_(0)/(2)+Ax)^(lambda))` CIn the
`P_(2)` `P_(1)` `(P_(1)(V_(0)/(2))^(lambda))/((V_(0)/(2)+Ax)^(lambda))` `(P_(2)(V_(0)/(2))^(lambda))/((V_(0)/(2)+Ax)^(lambda))` CIn the  `(V_(b))/(V_(c))` `(V_(c))/(V_(b))` `(V_(d))/(V_(a))` `V_(b)V_(e)` AA light ray from air is incident (as shown in figure) at one end of a glass fiber (refractive index `mu = 1.5`) making an incidence angle of `60^(@)` on the lateral surface, so that it undergoes a total internal reflection. How much time would it
`(V_(b))/(V_(c))` `(V_(c))/(V_(b))` `(V_(d))/(V_(a))` `V_(b)V_(e)` AA light ray from air is incident (as shown in figure) at one end of a glass fiber (refractive index `mu = 1.5`) making an incidence angle of `60^(@)` on the lateral surface, so that it undergoes a total internal reflection. How much time would it  `3.33 mu sec` `6.67 mu sec` `5.77 mu sec` `3.85 mu sec` D N/AA combination of two thin lenses with focal lengths `f_(1)` and `f_(2)` respectively forms an image of distant object at distance 60 cm when lenses are in contact. The position of this image shifts by 30 cm towards the combination when two lenses are separated by 10 cm . The corresponding values of `f_(1)` and `f_(2)` are 30 cm, -60 cm 20 cm, -30 cm 15 cm, -20 cm 12 cm, -15 cm B N/AAn optical instrument uses a 25 D objective and 20 D eyepeice with a tube length of 25 cm when eye is least strained The instrument is a telescope with angular magnification 20. The instrument is a microscope with angular magnification 20. The instrument is a telescope with angular magnification 24. The instrument is a microscope with angular magnification 24. B N/AThe ratio of d-Brogile wavelength off mlecules of hydrogen and helium gas moving at arms speed in two gas jars kept sparately at temeperature `37^(@)` C and `127^(@)` C respectively is : `(2)/sqrt(3)` `sqrt(2/(3))` `sqrt(3)/(2)` `sqrt(8/(3)` DAt t=O, light of intensity `10^(12)` photons/` s-m^(2)` of energy 6eV per photon starts falling on a plate with work founction `2.5 eV` If area of the plate is `2xx10^(-4) m^(2)` and for every `10^(5)` photons one photoelectron is emitted, charge on the plate at t=25 s is `8xx10^(-15) C` `4xx10^(-14) C` `12xx10^(-10) C` `16xx10^(-12) C` ARadius of an electron moving in a circle in constant magnetic field is two times that of an `alpha` particle in the same field. Then de-Broglie wavelength of electrons is x-times of the `alpha`-particle Here x is1A telescope has an objective lens of `10cm` diameter and is situated at a distance of one kilometre from two objects. The minimum distance between these two objects, which can be resolved by the telescope, when the mean wavelength of light is `5000 Ã…`, of the order of mm is :5 Resolving limit of telescope is
`3.33 mu sec` `6.67 mu sec` `5.77 mu sec` `3.85 mu sec` D N/AA combination of two thin lenses with focal lengths `f_(1)` and `f_(2)` respectively forms an image of distant object at distance 60 cm when lenses are in contact. The position of this image shifts by 30 cm towards the combination when two lenses are separated by 10 cm . The corresponding values of `f_(1)` and `f_(2)` are 30 cm, -60 cm 20 cm, -30 cm 15 cm, -20 cm 12 cm, -15 cm B N/AAn optical instrument uses a 25 D objective and 20 D eyepeice with a tube length of 25 cm when eye is least strained The instrument is a telescope with angular magnification 20. The instrument is a microscope with angular magnification 20. The instrument is a telescope with angular magnification 24. The instrument is a microscope with angular magnification 24. B N/AThe ratio of d-Brogile wavelength off mlecules of hydrogen and helium gas moving at arms speed in two gas jars kept sparately at temeperature `37^(@)` C and `127^(@)` C respectively is : `(2)/sqrt(3)` `sqrt(2/(3))` `sqrt(3)/(2)` `sqrt(8/(3)` DAt t=O, light of intensity `10^(12)` photons/` s-m^(2)` of energy 6eV per photon starts falling on a plate with work founction `2.5 eV` If area of the plate is `2xx10^(-4) m^(2)` and for every `10^(5)` photons one photoelectron is emitted, charge on the plate at t=25 s is `8xx10^(-15) C` `4xx10^(-14) C` `12xx10^(-10) C` `16xx10^(-12) C` ARadius of an electron moving in a circle in constant magnetic field is two times that of an `alpha` particle in the same field. Then de-Broglie wavelength of electrons is x-times of the `alpha`-particle Here x is1A telescope has an objective lens of `10cm` diameter and is situated at a distance of one kilometre from two objects. The minimum distance between these two objects, which can be resolved by the telescope, when the mean wavelength of light is `5000 Ã…`, of the order of mm is :5 Resolving limit of telescope is 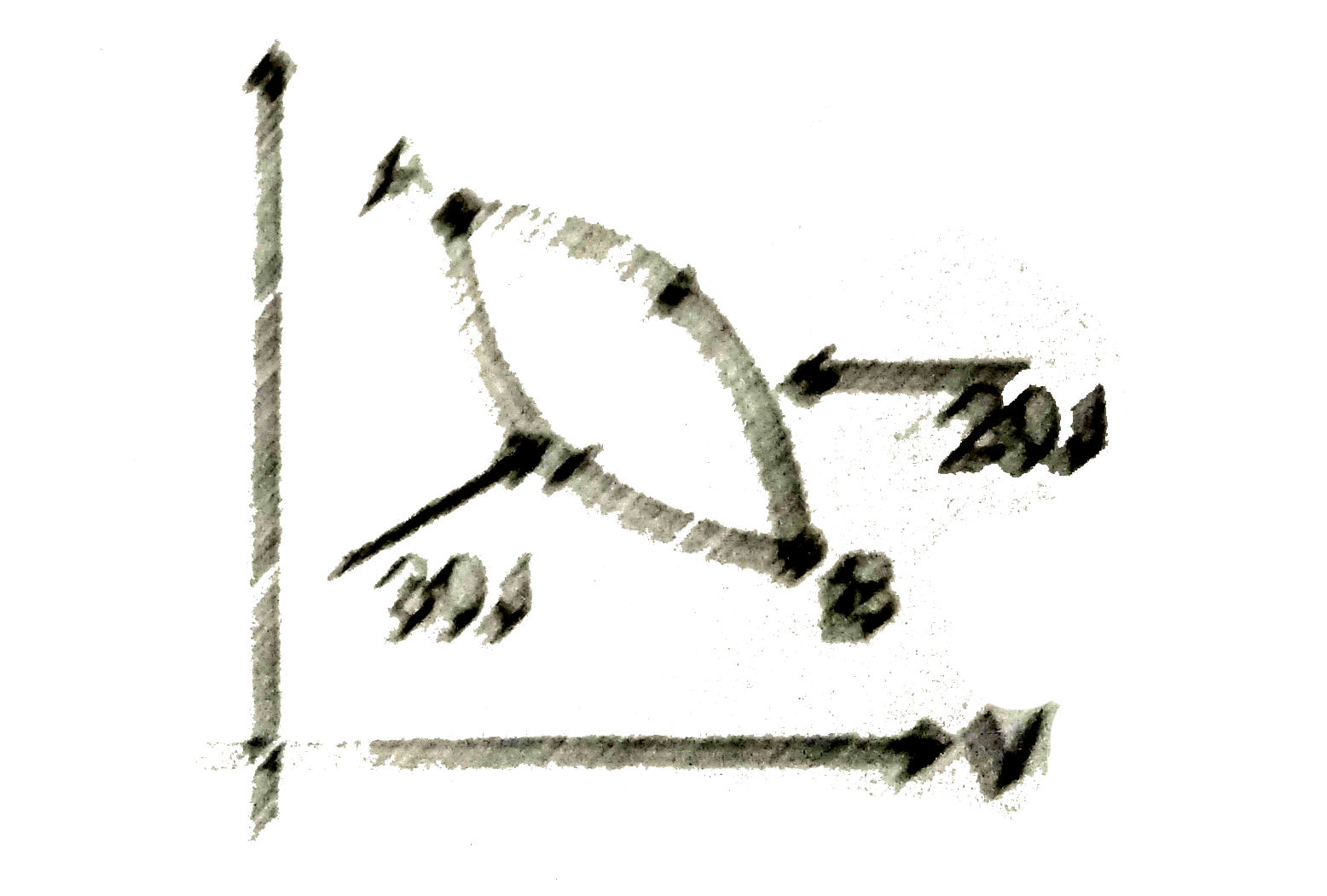 30 N//A
30 N//A