Construct a rectangle whose adjacent sides are of lengths 5cm and 3.5c

1.	Construct a rectangle whose adjacent sides are of lengths 5cm and 3.5cm .
Answer» Solution :We know that each angle of a rectangle is right angle (i.e., `90^(@)`) and its opposite sides are equal and parallel. To construct a rectangle whose adjacent sides are of lengths `5cm` and `3.5cm` use the following steps (i) Draw a line segment `BC` of length `5cm` . (ii) Now, GENERATE an angle of `90^(@)` at points `B` and `C` of the line segment `BC` and plot the parallel lines `BX` and `CY` at these points. (iii) Cut AB and CD of length `3.5cm` from BX and CY, respectively. (IV) Draw and angle `90^(@)` at one of the POINT A or D and join both points by a line segment AD of length 5cm. THUS , ABCD is the required rectangle with adjacent sides of length 5cm and `3.5cm` 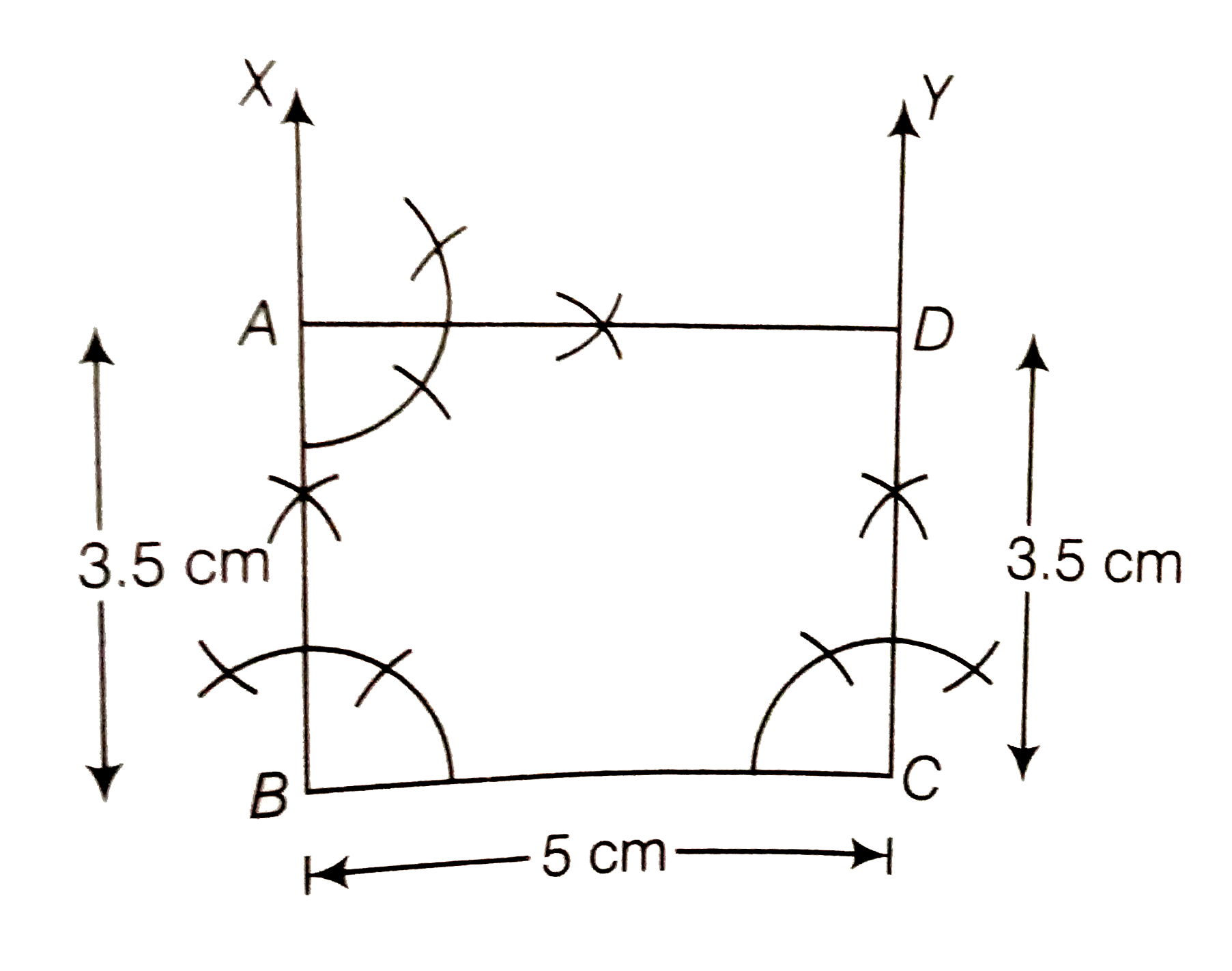Alternate Method To construct a rectangle `ABCD` whose adjacent sides are of lengths `5 cm` and `3.5cm`, use the following steps (i) Draw a line segment `BC` of length 5cm. (ii) Now, draw an `angleXBC - 90^(@)` at point `B` of line segment `BC`. (iii) Cut a line segment AB = `3.5cm` from the ray `BX` and join `AC`. (iv) Now, from A, point D is at a distance of 5cm. So, having `A` as centre draw an arc of radius 5cm. (v) From C, point D is at a distance of `3.5cm` . So, having C as centre draw an arc of radius `3.5cm` which intersect previous arc (obtained in STEP iv) at D. (vi) join `AD` and `CD`. Thus, `ABCD` is the required rectangle with adjacent sides of length `5cm` and `3.5cm` .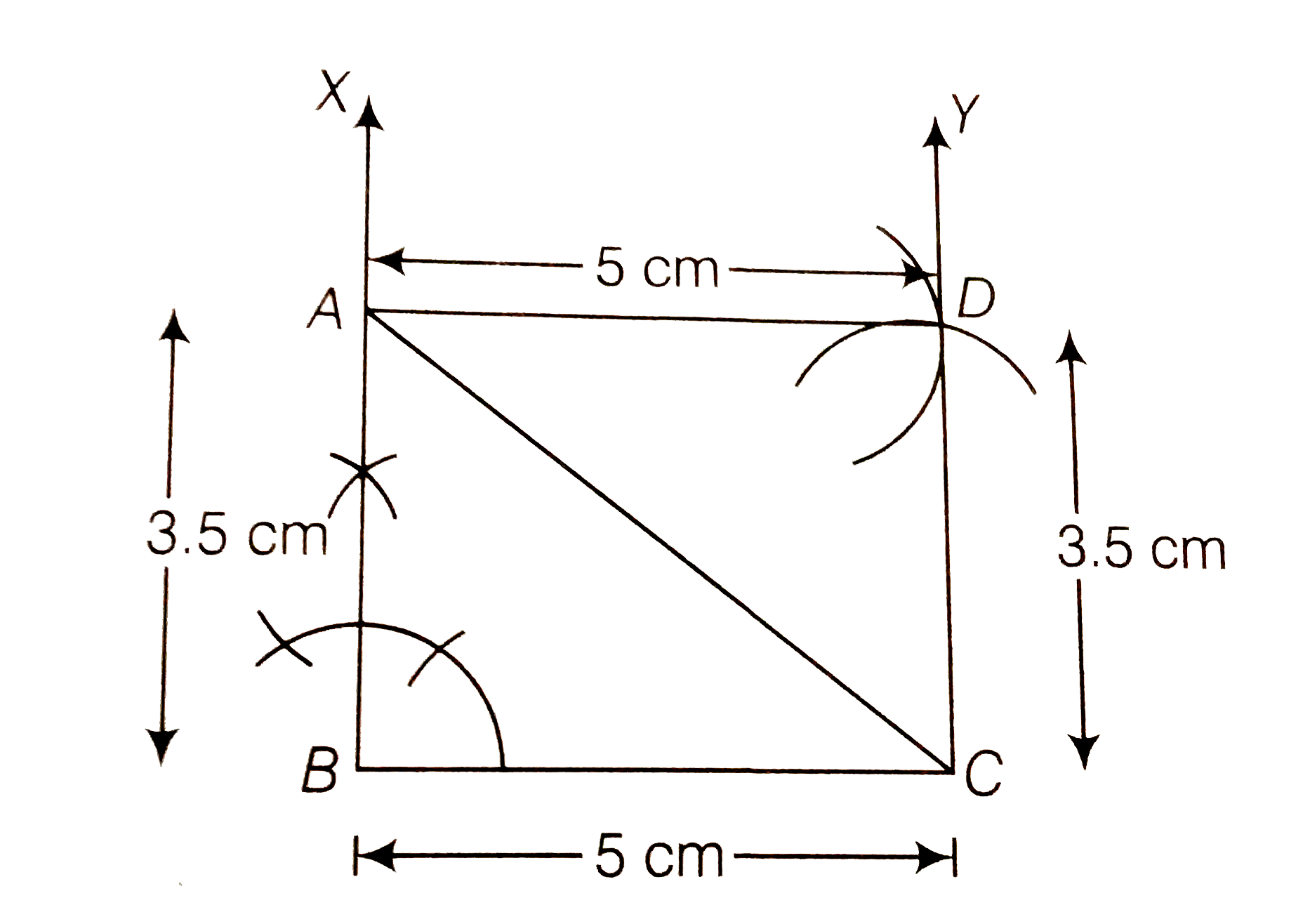

Discussion