1.

Factorise : (2x^(2)+5x)(2x^(2)+5x-19)+84

Answer»

Solution :LET `2x^(2)+5x=a`
`therefore ` GIVEN expression reduces to
`a(a-19)+84=a^(2)-19a+84`
Here, a=1, b=-19, c=84
`therefore ac=1xx84=84`
Now, we take two factors of 84 whose sum is -19. Such factors are -7 and -12.
`therefore a^(2)-19a+84=a^(2)-7a-12a+84`
`=a(a-7)-12(a-7)=a(a-7)(a-12)`
`=(2x^(2)+5x-7)(2x^(2)+5x-12)`
Similarly, these can also be factorised further.
`2x^(2)+5x-7=2x^(2)+7x-2x-7`
=(2x+7)-1(2x+7)
=(2x+7)(x-1)
and `2x^(2)+5x-12=2x^(2)+8x-3x-12`
=2x(x+4)-3(x+4)=(x+4)(2x-3)
`therefore` From (1), (2) and (3), we GET
`(2x^(2)+5x)(2x^(2)+5x-19)+84`
`=a^(2)-19a+84 "" ("where" a=2x^(2)+5x)`
=(2x+7)(x-1)(x+4)(2x-3)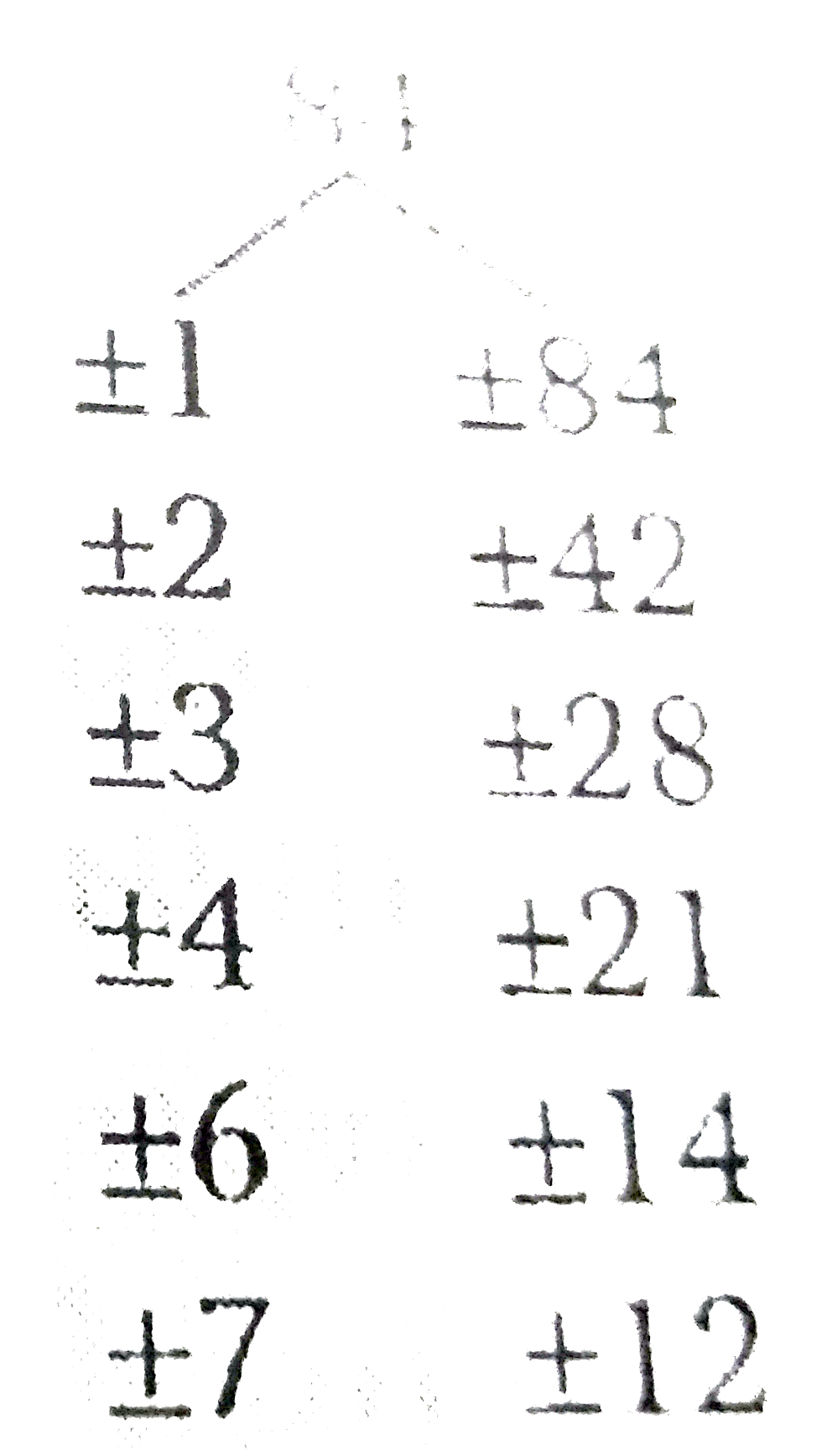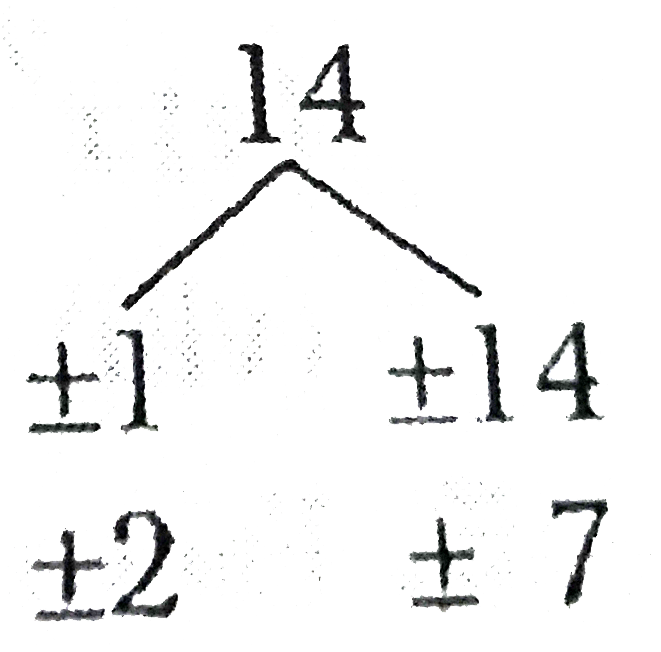




Discussion

No Comment Found

Related InterviewSolutions