1.

If the hypotenuse of an isosceles right triangle is 7 sqrt2cm, find the area of the circle inscribed in it

Answer»

Solution :LET AB = BC = x cm
`:.` In right `Delta ABC`, by Pythagoras theorem
`x^(2) + x^(2) = (7sqrt2)^(2)`
`rArr 2x^(2) = 98 rArr x^(2) = 49 rArr x = 7 cm`
`:. AR (Delta ABC) = ar(Delta AOB) + ar(DELTABOC) + ar(Delta COA)`
`(1)/(2) XX x xx x = (1)/(2) xx x xx r + (1)/(2) xx 7 sqrt2 xx r`
`rArr 7 xx 7 = 7 xx r + 7 xx r + 7sqrt2 xx r rArr r = (7)/(2 + sqrt2)`
`rArr r = (7)/(2 + sqrt2) xx (2 - sqrt2)/(2 - sqrt2) = (7(2 - sqrt2))/(2)`
`:.` Area of circle `= pi r^(2)`
`= (22)/(7) xx (49(2 - sqrt2)^(2))/(4) = (77)/(2) xx (4 + 2 - 4 sqrt2)`
`= 77 (3 - 2 sqrt2) cm^(2)`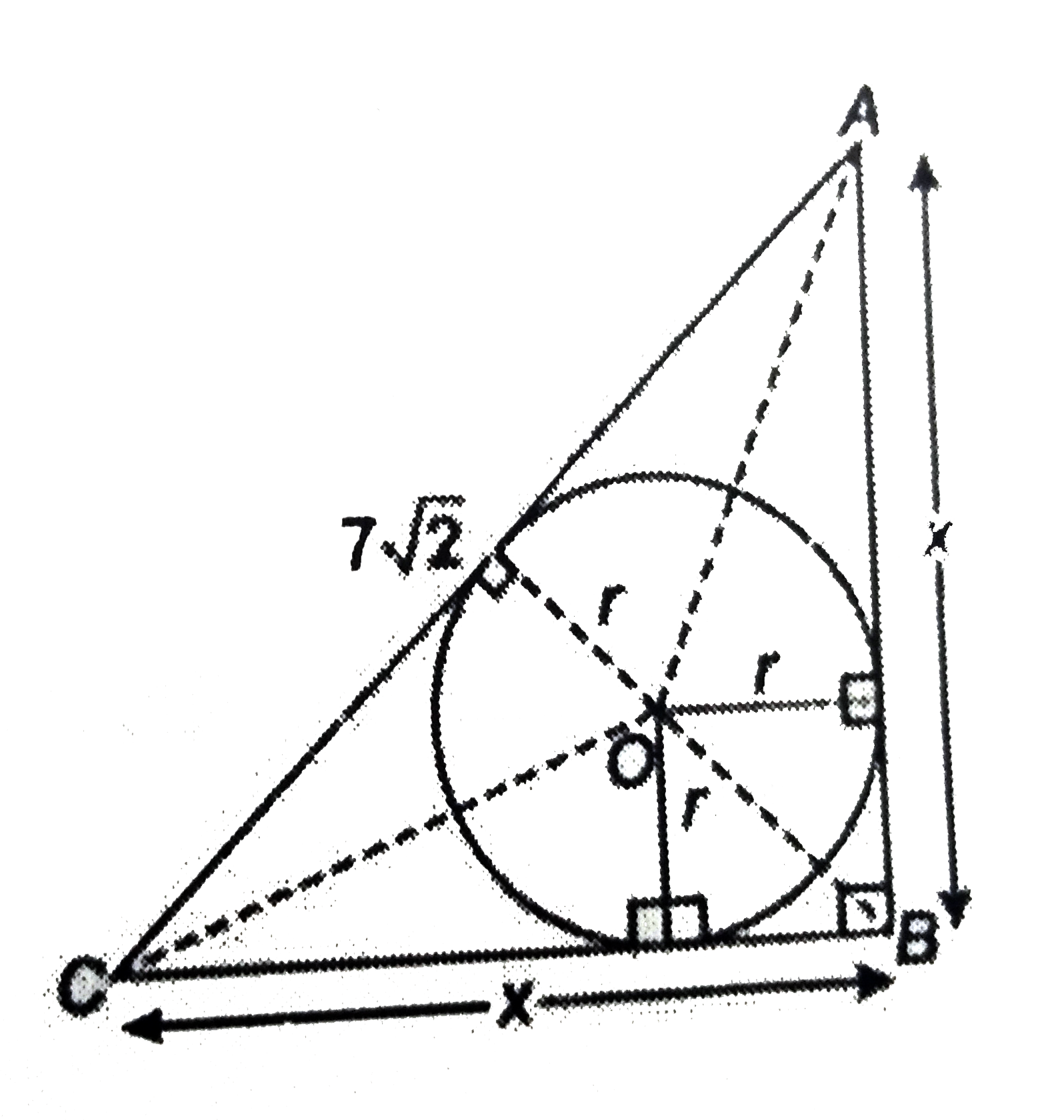


Discussion

No Comment Found

Related InterviewSolutions